箱桁组合钢梁斜拉桥剪力滞效应分析

马 国 峰

(山西交通职业技术学院，山西 太原 030031)

箱桁组合钢梁斜拉桥剪力滞效应分析

马 国 峰

(山西交通职业技术学院，山西 太原 030031)

以某在建大跨度公铁两用斜拉桥为背景，建立了箱桁组合整体有限元模型。对整体钢箱桥面的剪力滞效应进行了分析，并研究横隔板间距、桥面板厚度和箱梁截面高度等参数对桥梁剪力滞效应的影响规律。结果表明：箱桁组合钢梁中整体钢箱桥面存在一定的剪力滞后现象，边跨由于应力水平较低和支座处受力复杂导致剪力滞后效应较明显，过渡墩支点处最大应力不均匀系数为9.27；中跨大部分节段剪力滞后效应较小，顶板应力不均匀系数在1.06左右，底板应力不均匀系数在1.09左右，顶板应力均匀程度高于底板；从中跨跨中向桥塔方向，应力不均匀系数逐渐减小；随着横隔板间距、桥面板厚度和截面高度的增大，顶、底板应力不均匀系数减小，其减小值在5%以内。

桥梁工程；箱桁组合钢梁；剪力滞效应；横隔板间距；桥面板厚度；截面高度

翼板中法向应力沿横向分布不均匀的现象称为剪力滞效应[1]。剪力滞最早在航空航天工程中由于其存在大量的薄板结构受力后正应力不均匀现象严重而引起重视，后被引入土木结构工程中。薄壁钢箱梁有着优越的抗弯、抗扭和抗剪等受力性能，被广泛应用于大跨度桥梁中[2-4]。

目前国内外已有一些关于钢箱梁剪力滞效应的研究。箱桁组合梁多用于公铁两用斜拉桥中，结构受力体系复杂，主梁截面宽度大，空间效应显著。目前国内外对于箱桁组合梁剪滞效应研究较少[5-6]，忽略剪力滞效应的影响，可能会低估主梁中的应力，从而造成结构的不安全[1]，因此有必要对箱桁组合钢梁的剪滞效应进行研究。

笔者以某在建大跨度公铁两用斜拉桥为工程背景，采用有限元法对大跨度箱桁组合钢梁斜拉桥的剪力滞效应进行分析，研究整体钢箱桥面横隔板间距、顶底板厚度以及顶底板间距对结构剪力滞效应的影响规律。

1 工程概况

某在建大跨度斜拉桥采用公铁两用双塔斜拉桥方案。孔跨布置为(140+462+1 092+462+140)m，主梁采用箱桁组合钢桁梁结构；横向为三主桁结构；上层通行公路，桥面采用与上弦杆焊接的正交异性板桥面结构；下层通行铁路，桥面采用与下弦杆焊接的整体钢箱桥面结构，与弦杆相接处内高2.2 m，截面最高处内高2.324 m，铁路桥面钢箱每隔2.8 m设置一道隔板，隔板两侧采用对称布置的竖向加劲肋和水平加劲肋。主桁采用Q370qE，Q420qE，Q500qE等3种规格高强桥梁结构钢材，弹性模量Es=2.1×105MPa，泊松比μs=0.3，线膨胀系数αs=1.2×10-5/℃。主梁横截面布置如图1。

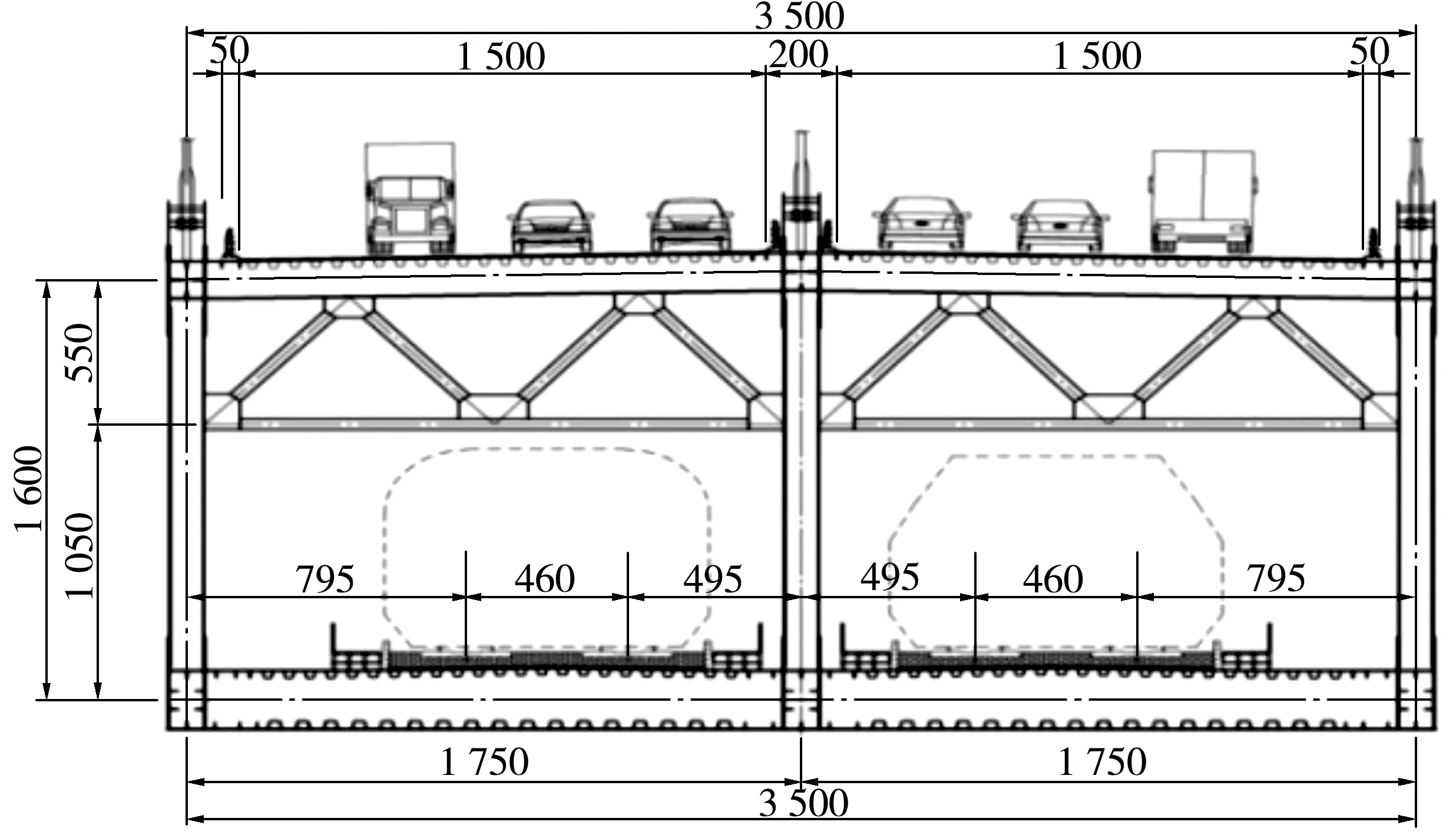
图1 箱桁组合梁横截面Fig. 1 Cross section of steel box-truss composite girder

2 剪力滞效应分析

2.1 分析模型

结合该桥的实际构造特点和计算精度的要求，运用有限元程序ANSYS，采用空间板梁单元法建立全桥模型，对铁路整体钢箱桥面顶、底板在恒载作用下的正应力分布特点进行分析。

模型中斜拉索采用三维杆单元模拟，并运用Ernst公式对其弹性模量进行修正[7]；桥塔、主梁上弦杆、腹杆、横联、桥面系加劲肋采用三维梁单元模拟；公路正交异性钢桥面板、铁路整体钢箱桥面顶、底板和横隔板采用壳单元模拟，考虑到铁路整体钢箱桥面板顶、底板的模拟的准确性，下弦杆也采用壳单元模拟，腹杆梁单元与下弦杆顶板之间通过建立刚性区域进行连接。公路桥面二期恒载取1.6 kN/m2，铁路桥面二期恒载取8.4 kN/m2。全桥有限元模型如图2。

图2 全桥有限元模型Fig. 2 Finite element model of overall bridge

2.2 计算结果分析

对翼板正应力横向分布不均匀的程度一般用剪力滞系数λ来衡量[8]：

λ=σmax/σinit

(1)

式中：σmax为截面最大正应力；σinit为在平截面假定下按初等梁理论计算的截面翼缘正应力，由于该箱桁组合梁结构复杂，按初等梁理论较难求出σinit，所以笔者以截面正应力平均值σaver代替σinit。

斜拉桥主梁截面正应力中单纯由弯曲产生的应力很小，轴力产生的正应力所占比重很大，弯曲对截面最终的应力不均匀程度影响有限[9-13]，所以传统以弯矩为主的剪力滞系数对工程应用意义不大。为便于工程应用又不与传统的剪滞系数概念混淆，笔者用应力不均匀系数代替剪力滞系数。

由于桥梁对称，取1/2全桥作为研究对象。根据模型计算结果，按式(1)对主桁铁路桥面各节点截面的纵向正应力进行分析，得到整体钢箱桥面顶、底板的纵向应力不均匀系数如图3。图4为两典型截面顶、底板纵向正应力横向分布。主桁节间距为14 m，1/2全桥共82个节段，节点号从梁端向跨中依次编为1～83。

由图3中可知：箱梁顶、底板均存在不同程度的应力不均匀现象。从应力不均匀系数沿桥纵向的分布来看，边跨节段变化较大，且在过渡墩和辅助墩处达到极值。这主要是由于在支座处有较大的集中反力作用，受力情况复杂，以及该处截面正应力水平较低所致。顶板最大剪力滞系数为8.16，底板最大剪力滞系数为9.27，均位于过渡墩支点处；在中跨节段变化较小，维持在一个比较稳定的水平，这主要和中跨支撑条件相近，应力水平较高且变化不大有关。单独从应力不均匀系数的大小来看对设计没有较大的指导意义。因为在应力不均匀系数最大的位置应力不一定最大，因此还需考虑截面的应力水平，两者结合对截面的应力进行控制。

从跨中向桥塔方向应力不均匀系数逐渐减小，这主要是因为越靠近桥塔，斜拉索的水平分力越大，且拉索轴力在主梁中经过几个节段的扩散后基本趋于均匀。

中跨大部分顶板应力不均匀系数在1.06～1.13之间，底板应力不均匀系数在1.09～1.32之间，顶板正应力分布均匀程度高于底板。由图4可知：顶板在腹板处应力小于截面中部应力，呈现负剪力滞现象，底板在腹板处应力大于截面中部应力，呈现正剪力滞现象。

图3 顶、底板应力不均匀系数纵向分布Fig. 3 Longitudinal distribution of uneven coefficient of stresses at top and bottom plates

图4 X=140 m和X=602 m处截面顶、底板正应力横向分布Fig. 4 Transverse distributions of stresses at top and bottom plates in X=140 m and X=602 m

3 参数敏感性分析

对影响剪力滞效应的因素进行敏感性分析，有助于深入了解剪力滞的变化规律，为桥梁的设计提供一定依据。以该桥的设计资料为基本参数，通过分别改变箱梁横隔板间距、顶底板厚度和箱型截面高度来研究这些因素对剪力滞效应的影响。根据截面应力水平和应力不均匀程度，选取中跨靠近桥塔处的5个节点截面作为参数敏感性分析的研究对象，分析剪力滞效应的变化规律。

3.1 横隔板间距对剪力滞的影响

大桥一个节段长14 m，铁路整体钢箱桥面横隔板间距为2.8 m，以此为基准，分别取横隔板间距为1.35，2，3.5，7 m进行比较分析，得到不同横隔板间距下顶、底板应力不均匀系数，如表1。

表1 不同横隔板间距下顶板和底板应力不均匀系数Table 1 Uneven coefficient of stresses at top plate and bottom plate with different transverse diaphragm distances

从表1可看出：随着横隔板间距的增加，顶、底板应力不均匀系数减小，截面正应力横向分布趋于均匀。这主要是由于增大横隔板间距，减少了一个节段内横隔板的数量，减小了顶、底板的约束，降低了翼板变形的阻力，使得翼板变形滞后程度减小。横隔板间距从1.35m增大到7m时，截面顶板应力不均匀系数最大减小了3.3%，底板应力不均匀系数最大减小了3.6%，增大横隔板间距对顶、底板应力的影响较一致。

3.2 顶、底板厚度对剪力滞的影响

剪力滞效应是由于远离腹板的翼板变形滞后造成的，因此翼板的厚度对于剪力滞后有一定的影响。以大桥整体钢箱桥面顶、底板厚度设计值为基准，铁路桥面钢箱顶底板厚度分为16，20，24 mm这3种。通过同时增大(+0.008，+0.016，+0.024 mm)或减小(-0.004 mm)顶、底板厚度分析其对剪力滞的影响。表2为不同桥面厚度下顶、底板应力不均匀系数计算结果。其中：H0为厚度设计值。

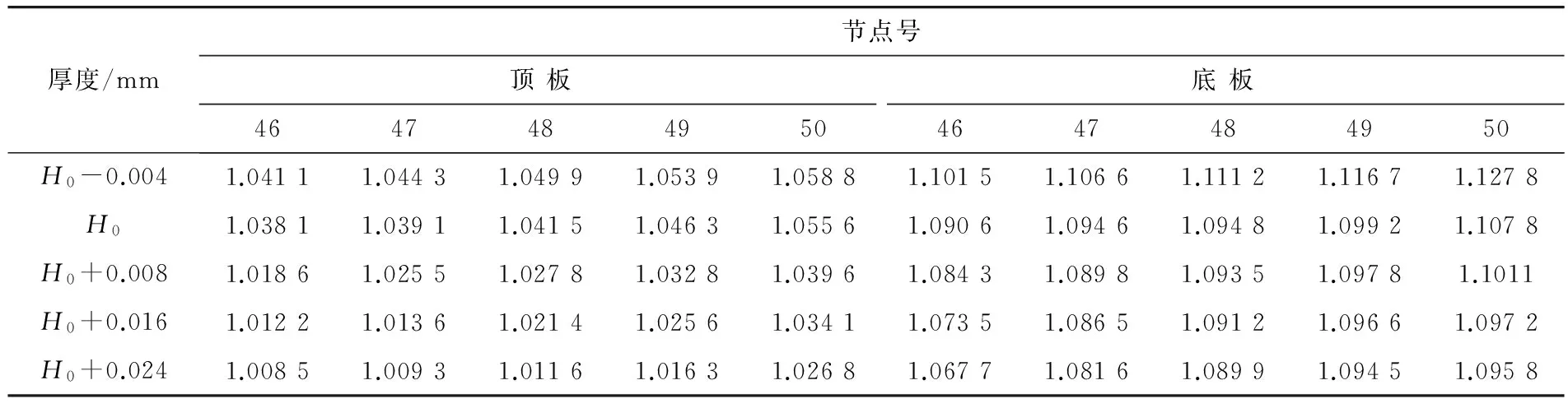
表2 不同桥面厚度下顶板和底板应力不均匀系数Table 2 Uneven coefficient of stress at top plate and bottom plate with different deck thickness

由表2可知：随着桥面厚度的增加，顶、底板应力不均匀系数减小，截面正应力横向分布趋于均匀。桥面厚度增加值从-0.004 mm增大到+0.024 mm时，截面顶板应力不均匀系数最大减小了3.9%，底板应力不均匀系数最大减小了2.3%，增大桥面厚度对顶板应力的影响要大于底板。

3.3 截面高度对剪力滞的影响

大桥铁路整体钢箱桥面与边桁下弦杆连接处内高2.2 m，忽略桥面横向坡度，以此为基准，分别取箱型截面高度为1.8，2.0，2.4，2.6 m进行比较分析，得到不同截面高度下顶、底板应力分布不均匀系数，如表3。

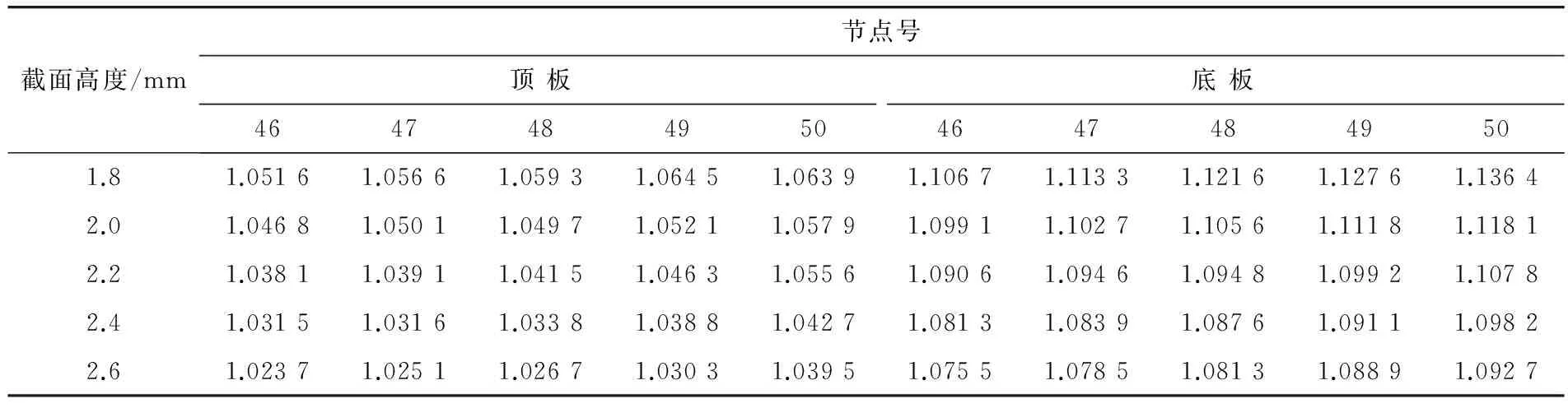
表3 不同截面高度下顶板和底板应力不均匀系数Table 3 Uneven coefficient of stress at top plate and bottom plate with different cross-section height

从表3可以看出：随着截面高度的增加，顶、底板应力不均匀系数减小，截面正应力横向分布趋于均匀。这主要是由于当截面高度增大时，远离腹板的翼板距离相对减小，剪力滞后效应减弱。截面高度从1.8 m增大到2.6 m时，截面顶板应力不均匀系数最大减小了2.9%，底板应力不均匀系数最大减小了4.2%，增大截面对顶板应力的影响要小于底板。

4 结 语

笔者以某在建大跨度公铁两用斜拉桥为背景，运用有限元分析方法对箱桁组合钢梁的剪力滞效应进行了研究。

分析计算结果得出：箱桁组合钢梁中存在一定的剪力滞后现象，边跨由于应力水平较低和支座处受力复杂导致应力集中，剪力滞后效应较明显，顶板最大应力不均匀系数为8.16，底板最大应力不均匀系数为9.27，均位于过渡墩支点处；中跨大部分节段剪力滞后效应较小，顶板应力不均匀系数在1.06左右，底板应力不均匀系数在1.09左右，顶板应力均匀程度高于底板；从中跨跨中向桥塔方向，应力不均匀系数逐渐减小。

结构参数敏感性分析表明：横隔板间距、桥面板厚度和截面高度对箱桁组合钢梁的剪力滞效应都有一定程度的影响。虽然增大桥面板厚度等可以减小剪力滞效应，但减小的幅度在5%以内，相对于增加的工程造价是不对等的，而且该桥主跨关键截面剪力滞效应本来就较小，因此桥梁的设计是合理的。

[1] 韦成龙，曾庆元，刘小燕．板桁结合梁剪滞效应分析的有限段法[J]．桥梁建设，2000(3)：11-13． WEI Chenglong, ZENG Qingyuan, LIU Xiaoyan. Finite segment method for analysis of shear lag effect in plate and truss composite girder[J].BridgeConstruction, 2000(3): 11-13.

[2] 陈勉．考虑剪力滞效应的钢-混凝土结合梁位移闭合解[J]．重庆交通大学学报(自然科学版)，2011，30(4)：717-720． CHEN Mian. Closed solutions of composite steel-concrete beams displacement considering shear lag effect[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2011, 30(4): 717-720．

[3] 苏庆田，吴冲，董冰．斜拉桥扁平钢箱梁的有限混合单元法分析[J]．同济大学学报(自然科学版)，2005，33(6)：742-746． SU Qingtian, WU Chong, DONG Bing. Analysis of flat steel-box-girder of cable-stayed bridge by finite mixed element method[J].JournalofTongjiUniversity(NaturalScience), 2005, 33(6):742-746.

[4] 陈红，谢军，黄成造．大跨度扁平钢箱梁斜拉桥主梁横隔板局部应力分析[J]．重庆交通大学学报(自然科学版)，2008，27(4)：508-511． CHEN Hong, XIE Jun, HUANG Chengzao. Local stress analysis in diaphragm of the long-span cable-stayed bridge with flat steel box-girder[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2008, 27(4): 508-511.

[5] YAMAGUCHI E, CHAISOMPHOB T, SA-NGUANMANASAK J, et al. Stress concentration and deflection of simply supported box girder including shear lag effect[J].StructuralEngineering&Mechanics, 2008, 28(2): 207-220.

[6] SA-NGUANMANASAK J, CHAISOMPHOB T, YAMAGUCHI E. Stress concentration due to shear lag in continuous box girders[J].StructuralEngineering&Mechanics, 2007, 29(7): 1414-1421.

[7] 孙淑红，顾安邦，张雪松．外倾式部分斜拉桥重庆嘉悦大桥锚固结构试验及受力分析[J]．重庆交通大学学报(自然科学版)，2011，30(增刊2)：1252-1255． SUN Shuhong, GU Anbang, ZHANG Xuesong. Cable girder anchorage experiment and stress analysis of extra-dosed cable-stayed bridge[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2011, 30(Sup 2): 1252-1255.

[8] 杨霞林，孙学先，吴亚平．斜拉桥箱形主梁直腹板的合理厚度分析[J]．铁道学报，2009，31(2)：132-136． YANG Xialin, SUN Xuexian, WU Yaping. Analysis of reasonable thickness of vertical web of main girder in cable-stayed bridge[J].JournaloftheChinaRailwaySociety, 2009, 31(2): 132-136.

[9] 罗许国，戴公连．三主桁斜拉桥桥面板剪力滞效应研究[J]．西安建筑科技大学学报(自然科学版)，2008，40(3)：297-301． LUO Xuguo, DAI Gonglian. Shear lag effect research of slab in three-truss cable-stayed bridge[J].JournalofXi'anUniversityofArchitectureandTechnology(NaturalScienceEdition), 2008, 40(3): 297-301.

[10] 张玉平，李传习．顶板、底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响[J]．长沙交通学院学报，2008，24(2)：23-28． ZHANG Yuping, LI Chuanxi. Influence of top flange, bottom flange and web thickness on the shear lag effect of box girder used in cable-stayed bridge[J].JournalofChangshaCommunicationsUniversity, 2008, 24(2): 23-28.

[11] KUNDALWAL S I, RAY M C. Shear lag analysis of a novel short fuzzy fiber-reinforced composite[J].ActaMechanica, 2014, 225(9): 2621-2643.

[12] GARA F, RANZI G, LEONI G. Short-and long-term analytical solutions for composite beams with partial interaction and shear-lag effects[J].InternationalJournalofSteelStructures, 2010, 10(4): 359-372.

[13] ZHOU Wangbao, JIANG Lizhong, YU Zhiwu. Analysis of free vibration characteristic of steel-concrete composite box-girder considering shear lag and slip[J].JournalofCentralSouthUniversity, 2013, 20(9): 2570-2577.

(责任编辑：刘 韬)

Shear Lag Effect of Steel Box-Truss Composite Girder of Cable-Stayed Bridge

MA Guofeng

(Shanxi Traffic Vocational and Technical College, Taiyuan 030031, Shanxi, P. R. China)

To analyze the shear lag effect of the overall box girder bridge deck, a finite element model of overall steel box-truss composite girder was established, which took a long span rail-cum-road cable stayed bridge in the construction as the research object. The influence rule of the transverse diaphragm distance, bridge deck thickness and cross-section height on the shear lag effect was also studied. The research results show that there are shear lag phenomena in the steel box-truss composite girder. Due to the low stress level and the bearing stress complexity, shear lag phenomena are more evident in the side span than in other areas. The uneven coefficient of maximum stress is 9.27 at the point of transition pier. The shear lag effect of most segments of middle span is small; the uneven coefficient of stress is 1.06 at top plate of and 1.09 at bottom plate; the stress uniformity of the top plate is higher than that of the bottom plate. The uneven coefficient gradually decreases from the middle section of middle span to the section near the tower. The stress uneven coefficient of top and bottom plates decreases with the increase of transverse diaphragm distance, bridge deck thickness and cross-section height, meanwhile its decreasing range is less than 5%.

bridge engineering; steel box-truss composite girder; shear lag effect; transverse diaphragm distance; bridge deck thickness; cross-section height

10.3969/j.issn.1674-0696.2017.05.02

2016- 04-11；

2016- 05-26

国家自然科学基金项目(51278222)

马国峰(1964—)，男，山西太原人，副教授，主要从事桥梁工程方面的研究。E-mail：395427372@qq.com。

U445.7

A

1674-0592(2017)05-007-05