隧道开挖引起深部土层位移的计算方法研究
田晓艳,刘 静,代建波
(西安石油大学 机械工程学院,陕西 西安 710065)
隧道开挖引起深部土层位移的计算方法研究
田晓艳,刘 静,代建波
(西安石油大学 机械工程学院,陕西 西安 710065)
基于平面应变原理,考虑岩土体的不可压缩性,采用国内外适用性较强的Peck公式验证所提出的考虑隧洞直径与上覆土层厚度、土体削减、盾尾间隙、围岩土质概况等因子对影响角参数、任意深度沉降槽宽度对数值的影响及取值区间。拟采用具体参数用于随机介质理论中,探讨了参数变化对Park位移模式3引起的隧道轴线上任一深度土层的三维空间位移的影响。通过相关具体算例结果表明:采用考虑围岩土体性质参数比较合理,且在工程上应用偏于安全。
岩土工程;围岩土质;Peck公式;主要影响角;沉降槽宽度系数;间隙参数
近年来为缓解城市的地面交通压力,减少环境污染且便于市民通行,各大中城市开始大规模的修建或扩建地下城市轨道交通系统。在城市中修建地下工程多数采取暗挖法[1],无论是选择新奥法施工、盾构法施工或者是其他方法施工,均会引发周围岩体向开挖空间体移动,破坏了土体的原始应力场分布,从而必然危害周边一定领域的环境。晋学辉等[2]采用ANSYS软件研究了重庆渝州隧道原位扩建施工对地表沉降的影响;刘洁等[3]采用MIDAS软件研究了西安地铁2#线锚杆系统对地表沉降的影响。由于有限元建模的复杂性以及耗时性,所以笔者拟采用解析法研究隧道开挖对土体变位的影响。
盾构[4-5]工艺引发土体变形的因素包括:掘进期间由于刀盘旋转切削土体产生的正面摩擦力引起的土体变形;掘进期间由于开挖面前面的助力引起的土体变形;掘进期间由于机身长度方向与周边土体接触产生的侧面摩擦力引起的土体变形;盾尾空隙由于土体损引起的土体变形等。铁富忠等[6]的研究表明:众多影响因素中引起土体变形的主要因素是盾尾空隙产生的土体损失,在工程实际中采取及时的同步注浆来减小其效应,但施工中浆液很难饱满且匀称的填补其盾尾空隙,所以产生较大土层位移是不可避免的。因此研究土体损失引发的间隙参数对其土体变形的影响规律有其迫切的现实意义。
1 深层土体沉降Peck修正经验公式
1.1 Peck经验公式
国内诸多地区如:北京、广州、武汉、西安等城市通过实际工程验证了采取传统的Peck理论[7]初估地面沉降的通用性,如图1。
(1)
引用不排水假设得:
VS=VL=πRg0+0.25πg02
(2)
式中:S(x,z)为任意位置x处的地表竖向位移;Smax为z=0处地表最大竖向位移;i为地面沉降槽宽度系数;VL为土体损失体积。
对于给定的工程,即已知R,H,则S(x,z)取决于VL和i两个参数:VL量化了地表沉降,i定性了地表沉降槽曲线的具体形状,即宽浅型或窄深型。
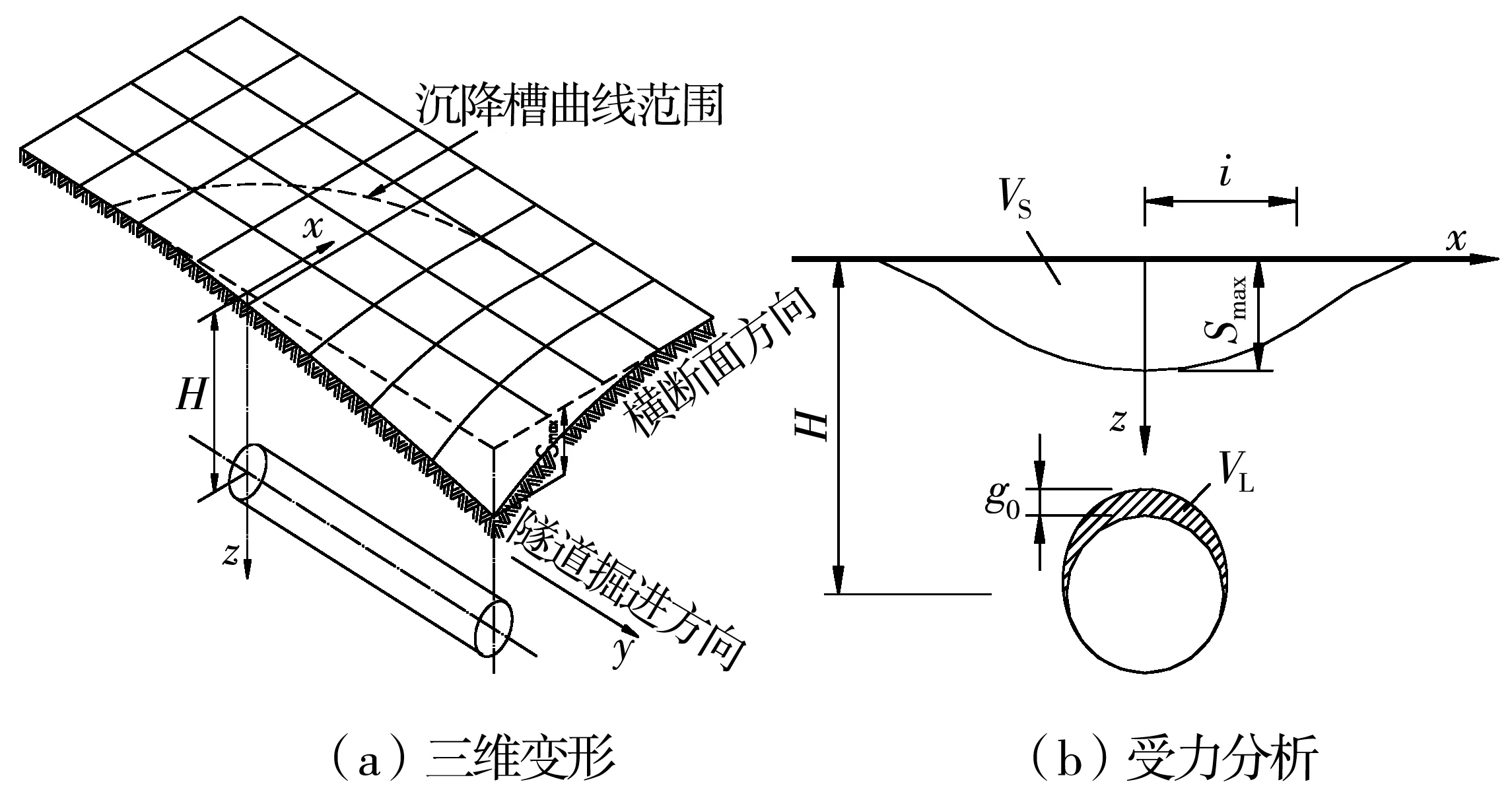
图1 隧道开挖引起的地面三维变形Fig. 1 Three dimensional ground deformation induced by tunnel excavation
1.2 隧道轴线上方土体沉降
R.J.MAIR等[8]认为:地表下任意深度土层的横向沉降槽亦符合正态分布,即:“高斯曲线”:
i(z)=kz(H-z)
(3)
kz=[0.5-0.325(z/H)]H/(H-z)
(4)
该理论在国内外文献被广泛采用。夏元友等[9]对式(4)进行了探讨,发现当z=0,kz=0.5时,与现实明显不符,其原因是:当土质不同时,kz是一个变化值,故针对式(4)需要进一步研究。目前统计资料列出典型的研究成果:姜忻良等[10]、魏纲[11]、韩煊[12]提出的3类改进kz;夏元友等[9]则通过具体工程算例,发现该3类kz曲线变化趋势是一致的,用于经验公式有其一定的适用价值,且在研究期间可进一步简化其计算成果。
笔者最终采用韩煊[12]的结论,即:
(5)
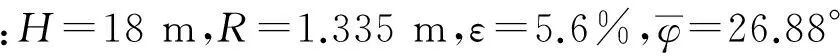
如前所述,地铁开挖引发围岩土体变形,土体变形亦必然引发基础变形。国内诸多研究学者如李早等[13]、熊巨华等[14]、王述红等[15]对隧道开挖引起的桩基效应进行了研究。
他们分别采取理论分析、试验研究和FEM有限元模拟进行探讨,且在理论分析中均采取两阶段法进行研究。阶段1采用L.P解[16],先求出任意位置处土体的自由场位移,之后为简化土体位移模式,均采取多项式进行拟合;阶段2将桩视为弹性地基梁,将阶段1所求得的土体位移作用在桩上,通过常数变易法或有限差分法,分别求解均质地基或非均质地基桩体的内力和位移。
图2为 Bangkok和Heathrow隧道工程的位移示意。由图2可知:L.P解[16]所求得的地表沉降值高于监测值,实际工程偏于安全;可地表下深部土体的沉降曲线与实测曲线不符,所以采取L.P解[16]求解土层深度的沉降有待商榷,且任意深度的沉降曲线分布形式受土隧间的相对位置影响很大,从而基于L.P解[16]求得的桩基效应结论亦值得探讨。
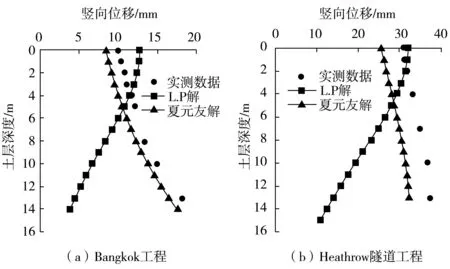
图2 Bangkok和Heathrow隧道工程位移Fig.2 Displacement of Bangkok and Heathrow Tunnel projects
夏元友等[9]基于Peck理论,选取韩煊[12]提出的沉降槽宽度系数结论,通过简单推导所得的深层土体竖向位移曲线与实测曲线趋势基本一致,且该结论得到王占生等[17]的证实,故算例1、2再次验证了Peck理论计算深层土体竖向位移的通用性。
1.3 隧道轴线上方土体的水平位移
开挖单元体必然引起土层的竖向位移,从而产生土层相应的水平位移。假定岩体不可压缩且在宏观上是连续的[18],得z处的水平位移u(x,z):
(6)
其中:边界条件为x=0;u(x,z)=0。
1.4 参数选用
根据夏元友等[9]选取的二要指标,为
VS=πRg+0.25πg2
(7)
(8)
(9)
在工程应用时,需要具备以下几个条件:① 根据地表的沉降槽监测数据,采用Peck公式拟合获得相应的参数V(s)和i(0)的取值;② 需要测斜管测得距离隧道某一位置的水平位移实测数据,然后对数据进行拟合得到参数α的取值;③ 根据地表沉降数据和水平位移数据,通过地层深度换算得参数k(z)的数值。
魏纲[19]通过22组实测资料数据研究亦表明:围岩土体性质决定i(z)的取值。故笔者拟用式(10)计算:
i(z)=i(0)(1-z/H)n=m[R+Htan(45°-φ/2)]×
(1-z/H)n
(10)
式中:φ为土体内摩擦角。
姬永红[1]的研究表明:盾尾间隙参数g0不仅与土体损失率有关,而且还与围岩的地质条件有关。故笔者拟用式(11)计算:
g0=2Rεtanφ
(11)
1.5 算例分析
1.5.1 参数的选取对结果的影响
选取前述算例进行剖析。由图3、图4可知:采用式(10)~式(11)计算的深层土体竖向和横向位移曲线变化趋势与监测值和夏元友等[9]的解一致,且笔者所提出的考虑围岩土体概况曲线值更接近实测值,相对于前人解在工程上使用更偏于安全。说明了围岩土体性质在参数选取中的重要性,亦验证了姬永红[1]和魏纲[19]结论的合理性。
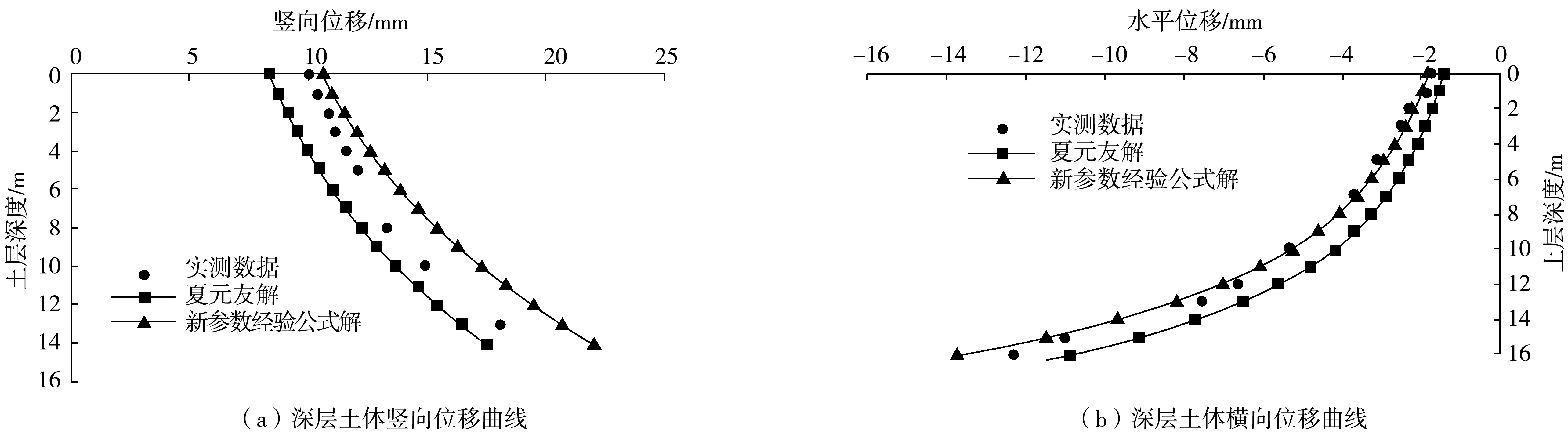
图3 深层土体竖向和横向位移曲线变化(Bangkok工程)Fig.3 Variation of vertical and horizontal displacement curves of deep soil(Bangkok project)
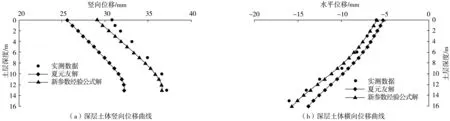
图4 深层土体竖向和横向位移曲线变化(Heathrow工程)Fig.4 Variation of vertical and horizontal displacement curves of deep soil(Heathrow project)
1.5.2 参数合理范围探讨
通过对式(10)~式(11)分析发现:影响数值的主要参数为:n为与隧道半径和土质条件有关的参数;φ为土体内摩擦角;ε为地层损失率;m为经验参数,其中:m∈(0.45, 0.50)。
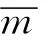
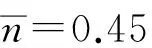
文中参数选取虽考虑了围岩土体的性质,但参数的取值范围很小且结果接近实测值;而夏元友等[9]的论述需要通过实测数据反分析获得参数α的数值,且如前所述,对于不同的土质情况,α范围较大,由此产生的误差亦较大,且计算结果均低于实测值,工程上偏于不安全。
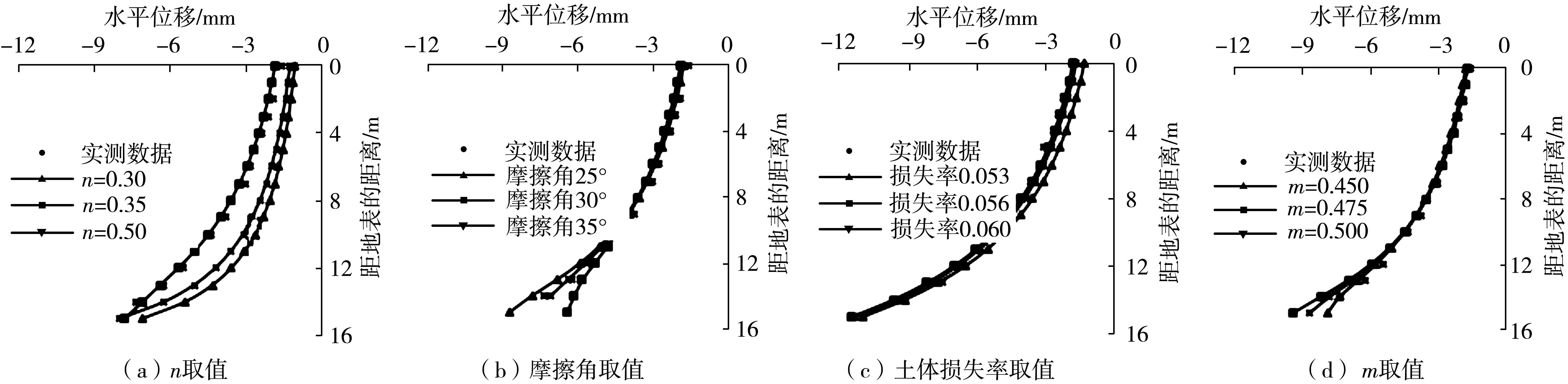
图5 参数范围结果对比(Bangkok工程)Fig.5 Parameter range comparison(Bangkok project)
2 土层随机方法探讨
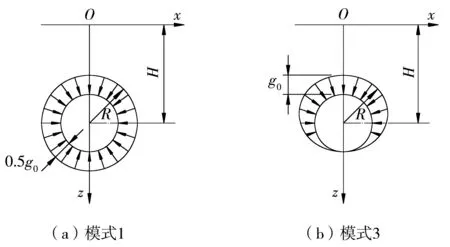
前述的经验法一般均假定隧道沿掘进方向无限长,即符合平面问题假定。但实测数据显示,地铁施工引发的土层位移是空间的,且业界认为:因子的多变性约束节理岩体的运动,该运动采取随机方法来探索,故将地下工程开挖视作随机过程。该思想经刘宝琛[22]和施成华等[23]的进一步研究。转化为概率积分法并建立相应的岩体位移表达式,该理论体系在预测地表移动已相当完善,但用于深层土体的空间位移尚待探究。尚需解决如下问题:① 合理选取深层土体的沉降槽宽度、间隙参数以及主要影响角;② 隧道横断面多发生Park提出的第3种非均匀径向位移模式。
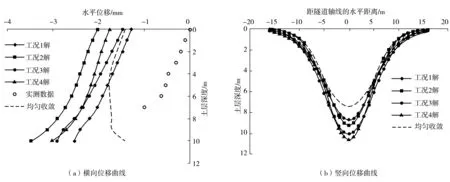
齐静静等[21]在施成华等[23]的基础上考虑了隧道底部为0的非均匀收敛模式,但在参数选取时,均未考虑围岩土体性质。姬永红[1]和魏纲[19]的研究结果表明:围岩土层性质对计算结果影响较大,所以笔者采取随机介质理论,比较分析Park的收敛位移模式1和模式3,得z 2.1 隧道中任意开挖单元引起的土体沉降 隧道开挖可视作无数微小单元开挖的叠加(图6),则利用随机介质理论[21]可得任意单元完全塌陷引起的单元沉降: (12) 图6 任意单元开挖的平面坐标Fig. 6 Plane coordinate diagram of excavation of arbitrary unit 2.2 隧道中开挖任意单元诱发土层横向位移 原理同1.3节,可得 ∂u(e)(x,y,z)/∂x+∂v(e)(x,y,z)/∂y+∂w(e)(x,y,z)/∂z=0 (13) 边界条件为 x=0,u(e)(x,y,z)=0;x→±∞,u(e)(x,y,z)=0 y=0,v(e)(x,y,z)=0;y→±∞,v(e)(x,y,z)=0 u(e)(x,y,z)= (14) v(e)(x,y,z)= (15) 2.3 隧道开挖引起土体的空间位移 设隧道开挖的初断面为Ω1,t→∞,竣工的终断面为Ω2,盾构机长度为l,半径为R(图7),若最大收缩为g0,则土层的空间位移为 [(x-ξ)2+(y-ζ)2]dξdζdη (16) [(x-ξ)2+(y-ζ)2]dξdζdη (17) (y-ζ)2]dξdζdη (18) 位移模式1: e=H-R+0.5g0,f=H+R-0.5g0 位移模式3: e=H-R+g0,f=H+R 图7 模式1和模式3径向位移收敛模式Fig.7 The first and third convergence modes of vertical displacement 以上推导的深层土体的空间位移公式均需要采用三重积分,且很难得到被积函数的原函数,故而采用数值积分通过计算机编程得到所求问题的解析解。 2.4 参数的取值 采取式(16)~式(18)时,重点是g0和βz的决择。βz为隧道上部岩体的主要影响角,由开挖所处的地层条件来确定,可查地勘资料,亦可根据量测资料反分析获得。βz与i(z)的关系可描述为 (19) g0与i(z)均与围岩土性有关,则可表示为 (20) 将Park公式的两种位移模式〔模式1(均匀收敛)和模式3(非均匀收敛)〕进行对比分析。其中:模式3又可分为以下4种工况: 工况3:g0=2Rεtanφ; 工况4:g0=2Rεtanφ; 图8为土层深度与位移的曲线。 由图8可知:模式1在计算近地表处的水平位移与模式3差别不大,但土层深部的水平位移变化趋势不同于实测曲线和模式3的变化规律,而且实际上由于隧道断面受诸多复杂因素的约束、土层的应力分布状态、施工工法和施工工序的选择、衬砌和注浆时间以及土体并非各向同性等,故而隧道并非呈规律的均匀性变化。 工况1与模式1均采用相同计算参数,但模式1所得的结论与B.VERRUIJT等[24]结论一致,即采取模式1计算的地表沉降曲线比实测曲线要宽,且侧向变形偏大的结论,所以基于模式3的随机介质理论的计算结果更为精确,且已得韩煊等[25]认可。 以模式3为基础的深层土体位移曲线中,4种工况曲线变化基本一致,且与实测曲线变化趋势一致,只不过实测数据是以地面为不动点进行监测的,工况1即国内研究学者齐静静解,取i(z)=i(0)(1-z/H)0.3,阐明n=0.3的正确性;工况1,3选用的土层影响角范围是相同的,工况2,4选用的间隙参数是相同的;由4组曲线结果发现,工况3,4数值比较接近,主要原因是选用的间隙参数是相同的,工况1,2数值差别较大。由此可知:参数土层主要影响角对结果影响很大,故而表明围岩土体性质对参数的影响是不容忽视的。 图8 深层土体横向和竖向位移曲线变化Fig.8 Horizontal and vertical displacement curves of deep soil 1)采用经典的Peck公式计算深层土体的沉降槽宽度系数时,不仅需考虑隧道自身状况(R,H),还需研究围岩的土质情况(m,n,φ)。 2)考虑围岩土体性质对参数进行分析时,认为n=0.3~0.6,m=0.45~0.5是合理的。m,n的取值范围都很小,故而产生的误差小,且在实际工程采用经验法初估位移时m,n均可取均值。 3)随机介质理论中采取模式3计算土体空间位移时,可避免由于模式1所得的隧道轴线正上方地表竖向位移偏小且沉降槽偏大和横向位移偏大的结论。 4)采用随机介质理论计算土层的空间位移时,必须考虑围岩土质情况对参数的影响。 [1] 姬永红.隧道施工引起横向地层沉降的随机预测[J].岩土工程技术,2004,18(1):16-18. JI Yonghong. Stochastic theory for predicting latitudinal stratum settlement due to the tunnel construction[J].GeotechnicalEngineeringTechnique, 2004, 18(1): 16-18. [2] 晋学辉,程崇国.大断面扩建隧道施工初期支护受力分析[J].重庆交通大学学报(自然科学版),2011,30(4):751-777. JIN Xuehui, CHENG Chongguo. Support mechanics analysis of enlarging tunnel with large cross-section at initial construction stage[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2011, 30(4): 751-777. [3] 刘洁,廖红建,顾飞,等.地铁隧道锚杆系统对地表沉降影响的数值分析[J].重庆交通大学学报(自然科学版),2012,31(增刊1):646-649. LIU Jie, LIAO Hongjian, GU Fei, et al. Numerical analysis for influence of bolt system in subway tunnel on ground settlement[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2012, 31(Sup1): 646-649. [4] 唐晓武,朱季,刘维,等.盾构施工过程中的土体变形研究[J].岩石力学与工程学报,2010,29(2):417-422. TANG Xiaowu, ZHU Ji, LIU Wei, et al. Research on soil deformation during shield construction process[J].ChineseJournalofRockMechanicsandEngineering, 2010, 29(2): 417-422. [5] 方勇,杨斌,杨志浩,等.地铁盾构隧道施工对地层扰动的影响因素分析[J].重庆交通大学学报(自然科学版),2014,33(1):36-41. FANG Yong, YANG Bin, YANG Zhihao, et al. Influence of metro shield tunnel construction on ground disturbance[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2014, 33(1): 36-41. [6] 铁富忠,支墨墨,张建安,等.盾构施工盾尾孔隙对地表沉降的影响分析[J].华东公路,2011(5):32-35. TIE Fuzhong, ZHI Momo, ZHANG Jianan, et al. The effect analysis of the ground settlement induced by the shield tail void[J].EastChinaHighway, 2011(5): 32-35. [7] PECK R B. Deep excavations and tunnel-ling in soft ground[C]//Proceedingsofthe7thInternationalConferenceonSoilMechanicsandFoundationEngineering. Mexico: Balkem-Aaa, 1969: 225-290. [8] MAIR R J, TAYLOR R N, BRACEGIRDLE A. Subsurface settlement profiles above tunnels in clays[J].Géotechnique, 1993, 43(2): 315-320. [9] 夏元友,陈春舒,BAKRI M,等.浅埋隧道开挖引起的土体水平位移分析[J].岩土力学,2015,36(2):354-360. XIA Yuanyou, CHEN Chunshu, BAKRI M, et al. Analysis of horizontal displacement of soil induced by shallow tunnel excavation[J].RockandSoilMechanics, 2015, 36(2): 354-360. [10] 姜忻良,赵志民,李园.隧道开挖引起土层沉降槽曲线形态的分析与计算[J].岩土力学,2004,25(10):1542-1544. JIANG Xinliang, ZHAO Zhimin, LI Yuan. Analysis and calculation of surface and subsurface settlement trough profiles due to tunneling[J].RockandSoilMechanics, 2004, 25(10): 1542-1544. [11] 魏纲.盾构隧道深层土体沉降槽宽度系数计算方法研究[J].公路交通科技,2010,27(4):110-115. WEI Gang. Study on calculation method of width coefficient of subsurface settlement trough in shield tunnel[J].JournalofHighwayandTransportationResearchandDevelopment, 2010, 27(4): 110-115. [12] 韩煊.隧道施工引起地层位移及建筑物变形预测的实用方法研究[D].西安:西安理工大学,2006:60-63. HAN Xuan.TheAnalysisandPrecictionofTunnelling-inducedBuildingDeformations[D].Xi’an: Xi’an University of Technology, 2006: 60-63. [13] 李早,黄茂松.隧道开挖对群桩竖向位移和内力影响分析[J].岩土工程学报,2007,29(3):398-402. LI Zao, HUANG Maosong. Analysis of settlement and internal forces of group pile due to tunneling[J].ChineseJournalofGeotechnicalEngineering, 2007, 29(3): 398-402. [14] 熊巨华,王远,刘侃,等.隧道开挖对邻近单桩竖向受力特性影响[J].岩土力学,2013,34(2):475-482. XIONG Juhua, WANG Yuan, LIU Kan, et al. Effects of tunneling on vertical bearing behaviors of adjacent single pile[J].RockandSoilMechanics, 2013, 34(2): 475-482. [15] 王述红,赵贺兴,姜磊,等.基于两阶段法地铁盾构开挖对邻近桩基影响分析[J].东北大学学报(自然科学版),2014,35(6):871-874. WANG Shuhong, ZHAO Hexing, JIANG Lei, et al. Analysis of the impact on adjacent pile caused by excavation with metro shield based on two-stage method[J].JournalofNortheasternUniversity(NaturalScience), 2014, 35(6): 871-874. [16] LOGANATHAN N, POULOS H G, STEWART D P. Centrifuge model testing of tunnelling-induced ground and pile deformations[J].Géotechnique, 2000, 50(3): 283-294. [17] 王占生,王梦恕,张弥.盾构隧道施工引起地表下土体变位的分析评估[J].岩土力学,2009,30(6):1699-1704. WANG Zhansheng, WANG Mengshu, ZHANG Mi. Methods for estimating subsurface ground movements induced by shield tunneling[J].RockandSoilMechanics, 2009, 30(6): 1699-1704. [18] ATTEWELL P B, YEATES J, SELBY A R.SoilMovementsInducedbyTunnelingandTheirEffectsonPipelinesandStructures[M]. London: Blackie, 1986. [19] 魏纲.盾构法隧道地面沉降槽宽度系数取值的研究[J].工业建筑,2009,39(12):74-79. WEI Gang. Study on calculation for width parameter of surface settlement trough induced by shield tunnel[J].IndustrialConstruction, 2009, 39(12): 74-79. [20] 姜忻良,李林,袁杰,等.深层地铁盾构施工地层水平位移动态分析[J].岩土力学,2011,32(4):1186-1192. JIANG Xinliang, LI Lin, YUAN Jie, et al. Dynamic analysis of strata horizontal displacements induced by shield construction of deep tunnel[J].RockandSoilMechanics, 2011, 32(4): 1186-1192. [21] 齐静静,徐日庆,魏纲.盾构施工引起土体三维变形的计算方法研究[J].岩土力学,2009,30(8):2442-2446. QI Jingjing, XU Riqing, WEI Gang. Research on calculation method of soil 3D displacement due to shield tunnel construction[J].RockandSoilMechanics, 2009, 30(8): 2442-2446. [22] 刘宝琛.随机介质理论及其在开挖引起的地表下沉问题中的应用[J].中国有色金属学报,1992,2(3):8-14. LIU Baochen. Stochastic medium model of surface settlement due to soil excavation[J].TheChineseJournalofNonferrousMetals, 1992, 2(3): 8-14. [23] 施成华,彭立敏,雷明锋.盾构法施工隧道地层变形时空统一预测方法研究[J].岩土力学,2009,30(8):2379-2384. SHI Chenghua, PENG Limin, LEI Mingfeng. Study of time-space united calculating method of stratum deformation caused by shield tunnel excavation[J].RockandSoilMechanics, 2009, 30(8): 2379-2384. [24] VERRUIJT B, BOOKER J R. Surface settlements due to deformation of a tunnel in an elastic half plane[J].Géotechnique, 1996, 46(4): 753-756. [25] 韩煊,李宁.隧道开挖不均匀收敛引起地层位移的预测模型[J].岩土工程学报,2007,29(3):347-352. HAN Xuan, LI Ning. A predicting model for ground movement induced by non-uniform convergence of tunnel[J].ChineseJournalofGeotechnicalEngineering, 2007, 29(3): 347-352. (责任编辑:刘 韬) Calculation Method Study of the Deep Soil Displacement Induced by the Tunnel Excavation TIAN Xiaoyan, LIU Jing,DAI Jianbo (School of Mechanical Engineering, Xi’an Shiyou University, Xi’an 710065, Shaanxi, P.R.China) First of all, based on the principle of the plane strain, considering the incompressibility of the rock and soil mass, the Peck formula which was quite applicable at home and abroad was applied. The influence of the factors considering the tunnel diameter, the buried depth, the soil cutting, the caudal space and the surrounding rock properties of soil factors on the influence angle parameter, the arbitrary width coefficients of seelement trough on the value and value range was verified by the Peck formula. Aand then, the proposed specific parameters were used in the stochastic medium theory. Finally,the influence of the parameter change on the three-dimensional displacement of the soil at arbitrary depth in tunnel axis caused by the third mode of the Park displacement mode was discussed. Through the relative case studies, the results show that:the parameters considering the nature of the surrounding soil are more rational and inclined to be safe in engineering application. geotechnical engineering; the surrounding soil; peck formula;major influence angle; width coefficients of settlement trough; gap parameter 10.3969/j.issn.1674-0696.2017.05.04 2016-04-10; 2016-06-29 国家自然科学基金项目(51405385);陕西省教育厅专项科研计划项目(15JK1562);西安石油大学博士科研基金项目(250205002) 田晓艳(1979—),女,陕西渭南人,讲师,博士研究生,主要从事土木工程方面的研究。E-mail:tianxy365@163.com。 U455.5 A 1674-0696(2017)05-017-07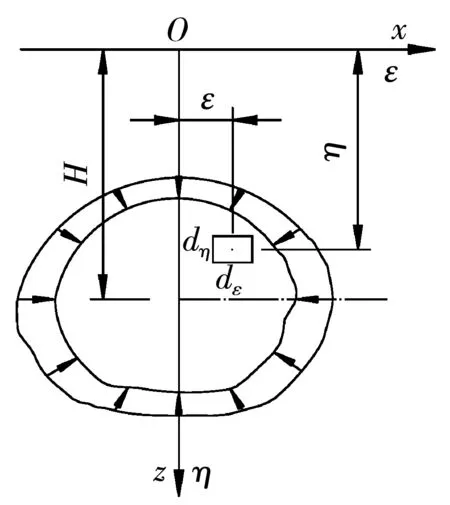
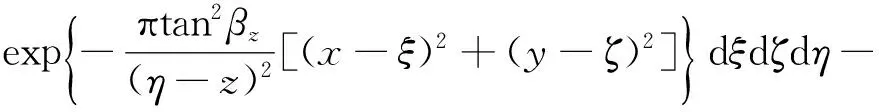
3 算例分析
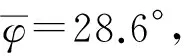
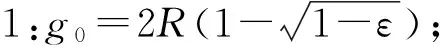
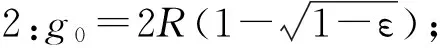
4 结 论

