考虑风速动态时空关系的风电功率预测

栗梦迪，董 哲，黄丽华，严敬汝

(1.河北农业大学 机电工程学院，河北 保定 071001；2.国网河北省电力公司培训中心，河北 石家庄 050000；3.华北电力大学 电气与电子工程学院，河北 保定 071003)

考虑风速动态时空关系的风电功率预测

栗梦迪1，董 哲2，黄丽华1，严敬汝3

(1.河北农业大学 机电工程学院，河北 保定 071001；2.国网河北省电力公司培训中心，河北 石家庄 050000；3.华北电力大学 电气与电子工程学院，河北 保定 071003)

风电间歇性和波动性强的特点使风电并网时给电力系统带来很大的安全风险，准确的风电功率预测可以有效提高电网安全运行特性。考虑风速动态关系的风电功率预测以数值天气预报(Numerical Weather Prediction，NWP)数据作为输入，分析了风电场局地效应和风向变化对流场的影响，建立了风电场局地效应模型及考虑风向影响的地形识别模型，通过模型对气流变化的物理过程进行解析求解，实现网格化NWP数据的修正，从而提高风速预报和风电功率预测的精度。最后，采用河北省某风场数据对风速和风电功率进行了预测，结果表明，所提出的预测方法能取得较为理想的预测效果。

风电功率预测；动态时空关系；NWP；局地效应

0 引言

随着风电大规模入网，风电波动性大的缺陷也日渐显露。对风电输出功率进行精确地预测可以对电网运行调度提供支持和指导，对风电入网的安全可靠性的提高有重大意义。

针对风电输出功率预测的研究主要以短期预测和超短期预测为主，采用的方法主要分为基于历史数据预测方法和基于数值天气预报数据的预测方法。基于历史数据的风电输出功率预测方法主要包括持续预测法[1]、卡尔曼滤波法(Kalman Filters)[2,3]、时间序列法[4,5]、空间相关性方法(Spatial Correlation)[6]、模糊逻辑法(Fuzzy Logic)[7,8]、人工神经网络法(Artificial Neural Network，ANN)[9]等

基于NWP的风电输出功率预测用于电网调度的风电输出功率短期预测时间尺度可长达数十h，采用数值天气预报数据作为输入量，能够较好地反映预测地点在预测时段内气象条件的变化[10]。然而，目前大多NWP数据的分辨率较低，以中尺度WRF(Weather Research and Forecasting)模式降尺度后，其计算网格水平边界仍保持在km及以上的数量级上，无法体现风电场局地效应对其风速分布造成的影响。因此，NWP数据作为“粗糙数据”不能直接用于功率预测，需要对其进行降尺度处理，折算到风电场待计算位置后再作为输入数据使用[11]。

基于此，考虑风速动态关系的风电功率预测首先对NWP数据的修正展开研究，建立风电场局地效应模型，通过对风电场局地效应的模拟实现NWP数据分辨率的提升。此后，以修正后的NWP数据作为输入数据，建立考虑风速动态时空关系的风电功率预测模型，对风电输出功率预测进行研究及算例验证。

1 风电场局地效应模型

风电场内地形及地表粗糙度的变化会对风电场的流场产生影响，这一现象称为风电场的局地效应[12]。风电场的局地效应对流场的影响属于非均匀下大气层的研究范畴，气象学上常采用的研究方法对研究人员的气象学专业知识水平提出了极高的要求。采用此类方法研究风电场局地效应对流场的影响时，结果的精度受数值天气预报网格分辨率的影响较大：提高数值天气预报的网格分辨率能使计算结果更加精确，但同时也会使计算时间大为延长。当分辨率过高时，甚至可能有超出中尺度NWP模式的假设条件而导致结果错误的现象出现。此外，气象学常用的研究方法所采用的各类模式自身也存在某些固有的缺陷。

本文采用解析法分析风电场局地效应对流场的影响，利用基于实验观测而建立的地表粗糙度变化模型和参考美国ASCE/SEI 7-05风荷载规范建立的地形变化模型对风电场局地效应进行模拟，并建立考虑风向影响的地形识别模型识别当前风向下气流路径。本节所提出的方法具有模型复杂度低、研究对象突出、工程实用性高的特点。

1.1 平坦地形的粗糙度变化模型

地表粗糙度是多相流体力学领域的一个综合力学参数，用于表征地表与大气之间的相互作用及物体表面对流经流体的阻滞力、流型、流态等影响[13]。地表粗糙度的变化将直接影响风廓线的分布，当气流从某种粗糙度的地表流向另一种粗糙度的地表时，风廓线将变得非常复杂。

NWP模式认为其各计算网格内下垫面的粗糙度为定值且分布均匀，基于该假设，可采用拜格诺对数风速廓线表示粗糙度对流经地表的气流的拖曳作用。而这只是一种理想情况，实际的风电场地表大多是非均匀的，如图1所示，受到地表粗糙度变化的影响，气流会在下风向形成新的内边界层[14]。

图1 粗糙度变化下风廓线变化示意图

显然，若气流在传递到研究位置的过程中历经地表粗糙度的变化，其风廓线将会发生改变。此时，对数风廓线的使用条件(均匀粗糙度)已不再成立，需建立新的表达式对受到粗糙度影响的风廓线重新进行描述。根据实验观测总结，考虑地表粗糙度变化影响的下风向风廓线可由式(1)表示。

(1)

式中：z01为与研究位置距离最近的上风向地表粗糙度；z02为待计算位置粗糙度。

(2)

(3)

式中：u*1、u*2分别为对应地表粗糙度z01、z02的摩阻流速；κ为Karman常数，通常取κ=0.41；h为内边界层高度，其值可根据下式确定：

(4)

式中：z0max=max(z01,z02)；d为粗糙度变化位置与待计算位置之间的水平距离。

为了准确反映地表粗糙度的情况，本文根据实测数据来确定粗糙度及摩阻流速的数值。将地表按照定床地表、动床地表、植被地表及建筑密集区3类进行划分。对于定床地表，只需测出同一地点上2个不同高度z1、z2对应的风速大小u(z1)、u(z2)，即可通过式(5)直接求出该位置的摩阻流速u*和粗糙度z0。

(5)

对于后两类地表，需首先通过观测或实验获得动床地表颗粒的临时起动风速和植被地表及建筑密集区的零面位移高度[15]，再利用同一地点2个不同高度风速的同时测量来对该地表下的摩阻流速和粗糙度进行计算。

1.2 复杂下垫面的地形变化模型

NWP数据是建立在计算网格内地形高度保持不变的假设上，通过流体力学及热力学方程组的计算得到的。而实际风电场往往有明显的地形起伏，为了更好地利用风能，风力发电机组及测风塔通常安装在地形高度较高处。受此影响，边界层气流与湍流应力均受到地形扰动，对数风廓线将发生变化。研究地形变化对风速的影响存在较大困难，本文参考美国现行的ASCE/SEI 7-05风荷载规范建立复杂下垫面的地形变化模型，模拟地形变化对气流的影响。

美国的风荷载规范是在Taylor“原始算法”基础上的发展与提高，可以反映典型的地形变化对近地风场的影响。相对于其他国家特别是发达国家的风荷载规范，美国规范考虑了地貌类别，即地表粗糙度对地形系数的影响，更具参考意义。

当风由开阔地形经过山坡、陡坡等变化地形时，将在变化地形表面距离地面一定高度内产生加速区，如图2所示。

风荷载规范将这种地形变化影响下风速的变化归因于风压的改变，由伯努利方程可得：

(6)

图2 地形变化对风廓线影响示意图

式中：ωp表示风动压；ρ为空气密度；v表示当前风速。

采用地形系数Kz表示地形扰动对风压的影响，地形系数表达式如下:

(7)

式中：K1表示考虑地形影响的最大增压因子；K2表示考虑上下风向与山顶间距离的折算因子，K2=[1-d/μL]，d为计算点与山顶位置之间的水平距离，L为山顶位置与山体高度一半处之间的水平距离；K3为考虑待计算位置高度的折算因子，K3=e-γz/L。其余变量K1、μ、γ均为常数，取值参见表1。

表1 ASCE/SEI 7-05规范参数参考取值

表1中地貌类型参考表2。

表2 ASCE/SEI 7-05标准中地貌类别的分类

在计算出地形系数Kz后，即可确定经地形扰动后的风压：

(8)

在气流历经地形起伏的过程中，其密度的变化十分微小，因此，在计算过程中可忽略空气密度的变化。

在给定计算点位置及周围地形变化信息后，联立式(6)-(8)即可计算出经地形变化后待计算位置的风速：

(9)

1.3 考虑风向影响的地形识别模型

在风电场实际运行的过程中，风向时刻保持动态变化的特性。当风向不同时，气流在NWP计算网格边界的起始点及其由起始点到达待计算点途经的路程存在差异。即在NWP的计算网格内，风可能起始于不同的位置，并经历不同的下垫面变化到达测风塔所在位置。因此，将风向的影响纳入考虑，建立考虑风向影响的地形识别模型具有重要意义。

以测风塔所在位置为坐标原点建立直角坐标系，将计算网格内下垫面俯视图等比例缩放，对于有明显变化的下垫面，用边界线将其划分出来，并形成边界线函数。对于任意风向角β，建立斜率为k=tan(π/2-β)的直线来表示风的走径。直线起始于其自身与计算网格边界线的交点，并终止于测风塔所在位置，根据直线与每一边界线函数的交点即可确定风在该地貌下所经过的路程。

2 考虑风速动态时空关系的风电功率预测步骤

本文以风电场外特性作为出发点，通过考虑风速动态时空关系的风电功率预测模型对风电输出功率进行预测，具体预测步骤如下：

步骤一：以数值天气预报数据作为输入数据，考虑风向影响的地形识别模型识别气流途经路线，读取途经路线中地形及地表情况。

步骤二：根据气流流经过程中地形、地表的变化，采用上文建立的风电场局地效应模型对NWP数据进行修正，修正后得到测风塔所在位置的预测风速。

步骤三：由风速动态分布模型确定机组的上下游排序，根据风切变指数规律式

(10)

对测风塔高度的预测风速进行折算，将其折算至最上游机组轮毂高度处。随后读取风电场内所有机组的运行状态，并通过风电场内风速动态时空分布特性的风速模型，模拟出气流在整个风电场内的分布，从而预测出各台风机的捕获风速。

步骤四：根据各台机组捕获风速的预测结果，结合比恩法所得到风速-功率曲线即可计算出各台风电机组的预测功率。

上述过程如图3所示。

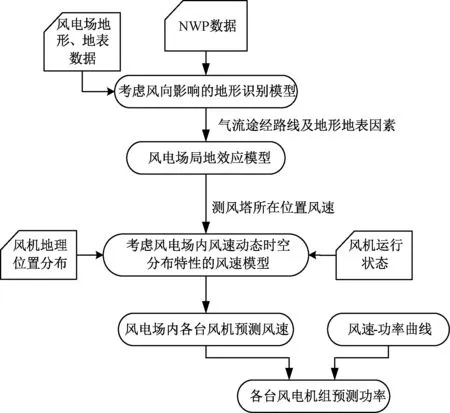
图3 考虑风速动态时空关系的风电功率预测步骤

3 算例分析

3.1 场站描述

本文采用河北省某风电场为研究对象，该场位于东经115°16′～115°26′、北纬40°48′～40°52′区域，地貌类型为中山。风电场地形呈平缓丘陵状，如图4所示，地形坡度约35°，为典型的山脊型风电场。主要用于机组布置的山脊呈东西走向，海拔集中在1 800 ～2 000 m之间。风机所在山体及风电场周围山体地表覆盖为耕织土及碎石、块石，厚度较薄，岩石主要岩性为花岗岩。风电场场区内配备有测风塔，测风塔海拔高度为2 035 m，位于整个场区最高点。

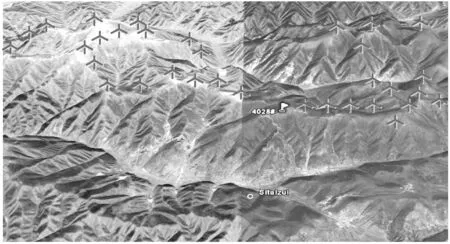
图4 风电场地形地貌示意图

3.2 NWP数据修正结果及其分析

根据上文所建立的风电场局地效应模型对NWP数据进行修正，模型以经WRF(Wather Research and Forecasting)模式降尺度后的NWP风速及风向时间序列作为输入数据，数据水平分辨率7 km，每15 min为一点。图5给出了24 h的测风塔实测风速曲线及同一时段内修正前后的NWP风速数据。

图5 NWP风速数据及其修正结果

为了更好地突出修正效果，采用风速变化较大情况下的数据进行算例验证。由图5可以看出，预报数据能够反映风速变化的整体趋势，这一优势在气象条件变化较大、较突然的情况下将表现得极为突出。但由于NWP数据的自身局限性，修正前后的数据都难以反映出风速高频率、小幅度的脉动。

经计算，修正前后NWP风速的均方根误差分别为2.306 0 m/s、1.075 8 m/s。图形及数据均表明，所提出的修正方法能够在一定程度上修正NWP数据的误差。分析可知，NWP数据的误差可认为由2部分组成：一部分是由于其模式分辨率不足造成的，主要表现在数据无法精确到计算网格内的某一具体计算点；另一部分是其自身的预报误差，主要与气象预报人员的经验及专业水平有关。本文所提出的修正方法主要是针对第一部分误差进行修正，而如何处理第二类误差还有待深入研究。

3.3 考虑风速动态时空关系的风电功率预测

按照调度要求，依据上文预测步骤对所研究风电场进行提前1 d的风电输出功率预测，预测时间分辨率为15 min。采用以下算例：

算例1：直接采用未经修正的NWP数据作为输入，经考虑风电场内风速动态时空分布特性的风速模型后，得到各台机组风速并通过功率曲线计算其输出功率。

算例2：在算例1的基础上，增加NWP数据修正的步骤，即采用本文所建立的考虑风速动态时空关系的风电功率预测模型，依据上文所述步骤进行预测。

算例3：以测风塔实时数据作为输入数据，通过风速模型计算出各台风机风速，然后再对其输出功率进行计算。由于该算例所使用的输入数据为测风塔实测数据，故该算例并未实现风速及功率的预测，仅作对比使用。

从各算例结果中提取WT1的输出功率与其实测功率对比如图6所示。

图6 不同算例下WT1的功率曲线

(1)在图6中，算例1及算例2的预测曲线与实测功率曲线的变化规律基本一致。这表明，气象条件是影响风机捕获风速及输出功率的决定性因素，采用NWP数据作为输入数据进行预测可以反映一段较长时间内风电场气象条件的变化，使预测结果能够较为准确地反映风速及功率的变化趋势。

(2)将图6中算例1及算例2的预测曲线分别与实测功率曲线进行对比，可发现：由于算例2实现了对NWP数据的修正，其预测曲线与实测曲线的吻合程度较算例1有显著提高。

(3)直观来看，各算例预测曲线与实测曲线的吻合程度以算例3、算例2、算例1的顺序递减。分析原因为，算例3采用实测测风塔风速作为输入数据，其曲线可以反映出算例1、2难以反映的功率高频、小幅的波动，避免了由于NWP数据自身的预测误差而造成的功率预测误差，故算例3的仿真精度最为理想。因此，合理的数据输入是提高预测精度的关键所在。

(4)图中，3条曲线与实测曲线的偏差主要集中在曲线末端部分。算例3的预测曲线与实测曲线在该部分的变化趋势基本一致，偏差主要表现为两曲线幅值的不同。而算例1及算例2的预测曲线与实测曲线在幅值及变化趋势上都存在较大差别。经分析，该现象可能是由于该时段数值天气预报误差较大，而算例1、2是基于NWP数据进行预测而导致的。

为了更好地对比各算例的预测效果，对上述算例的预测功率进行误差统计，结果如表3所示，表中MAE,RMSE均以百分数表示，其基准值为风电机组额定容量。

表3 不同算例下风电机组输出功率预测误差

对比算例1及算例2的误差数据，算例2的MAE及RMSE相较于算例1均下降了近十个百分点，这表明，对NWP数据进行修正，可以在一定范围内有效地降低预测误差。此外，通过算例2和算例3的误差数据可以看出，采用NWP数据与采用测风塔实测数据作为输入，其模型输出结果有明显差异。当采用测风塔实测数据作为输入时，模型的输出结果明显优于以NWP数据为输入时的预测结果。这表明，尽管已经对NWP数据进行了一定的修正，但其仍是误差的主要来源，若NWP数据精度较高，则所提出的预测方法将能取得较为理想的预测效果。

4 结论

(1)与NWP数据“等高、恒面”的假设不同，风电场内的地形起伏及地表情况的变化都将使其流场分布发生改变。采用风电场局地效应模型，通过考虑风向影响的地形识别模型、平坦地形的粗糙度变化模型、复杂下垫面的地形变化模型模拟气流由计算网格边界到达待计算位置的变化，可以在一定程度上修正由于NWP数据分辨率不足而造成的预测误差。

(2)通过考虑风速动态时空关系的风电功率预测方法，对预测风速进行解析求解及功率转换，可实现对未来几十h内风电出力的预测。特别地，当数值天气预报精度较高时，该方法可以取得较为理想的预测效果。由于该方法为基于解析算法的物理预测方法，故具有计算时间短、工程实用性强等优点，且在预测过程中无需使用到大量的历史数据。因此，该方法还可适用于新建风电场的功率预测或为风电场的选址优化、风机位置优化分布提供参考，具有一定实际应用价值。

[1]裴瑞平,田丽,魏安静,等. 短期风功率自适应加权组合预测[J].重庆工商大学学报(自然科学版),2016,33(2):26-29.

[2]范强,文贤馗,林呈辉,等. 风电功率预测方法研究[J]. 贵州电力技术,2016,19(10):12-20.

[3]杨茂,黄宾阳. 基于灰色缓冲算子-卡尔曼滤波双修正的风电功率实时预测研究[J]. 可再生能源,2017,35(1):101-109.

[4]牛晨光,游晓科,赵震云,等.风电场发电功率短期预测组合模型研究[J]. 华北电力大学学报(自然科学版),2012,39(3):29-34.

[5]石亚欣. 基于时间序列的WD-LS-SVM的风速周期预测模型研究[J]. 电力科学与工程,2014,30(2):41-45.

[6]徐梅梅,任祖怡,陈建国,等.基于空间相关性和小波-神经网络的短期风电功率预测模型[J].南京理工大学学报,2016,40(3):360-365.

[7]杨柳青,陈伟,赵伟,等. 风电场功率控制策略研究与应用[J]. 东方汽轮机,2014(3):55-61.

[8]栗然,李永彬,党磊. 基于短期机组组合的含风电场滚动优化调度研究[J]. 华北电力大学学报(自然科学版),2016,43(5):49-54.

[9]苏义鑫,夏慧雯. 用于风电功率预测的RPCL优化神经网络模型[J].北京工业大学学报,2016,42(5):674-678.

[10]王丽婕,冬雷,高爽. 基于多位置NWP与主成分分析的风电功率短期预测[J].电工技术学报,2015,30(5):79-84.

[11]李莉, 刘永前, 杨勇平, 等. 基于CFD流场预计算的短期风速预测方法[J]. 中国电机工程学报, 2013, 33(7): 27-32.

[12]白永清,陈正洪,陈鲜艳,等. 长江山区航道剖面能见度分析及局地影响因素初探[J]. 长江流域资源与环境,2015,24(2):339-345.

[13]张元元,吴振森,张玉石. 地表后向散射测量实验及其等效介电常数和粗糙度参数的反演[J]. 电波科学学报,2016,31(1):79-84.

[14]马高生, 黄宁. 风雪流临界起动风速的研究[J]. 兰州大学学报, 2006, 42(6): 130-134.

[15]刘刚. 中国与美国规范风荷载计算分析比较[J]. 钢结构,2010,12:47-52，79.

Wind Power Forecast Considering the Spatial Temporal Dynamics Relationship of Wind Speed

LI Mengdi1, DONG Zhe2, HUANG Lihua1, YAN Jingru3

(1.School of Mechanical and Electrical Engineering, Agricultural University of Hebei, Baoding 071001,China;2. State Grid Hebei Training Center, Shijiazhuang 050000,China; 3. School of Electric and Electronic Engineering,North China Electric Power University, Baoding 071003,China)

Due to the intermittent and fluctuant features of wind power, large scale grid integration of wind power brings a severe challenge to the safe operation of electric power system. The accurate prediction of wind output power can provide an important reference and solid support for the control and operation of the power grid. Using the NWP (Numerical Weather Prediction)data as input, the wind farm local effect and the influence on low field caused by wind direction change are analyzed, and meanwhile, the local effect model of wind farm and the terrain identification model considering wind direction are also discussed in this paper. The physical process of air flow is simulated by the proposed model, and the goals of realizing the correction of NWP data and improving the prediction accuracy are achieved. Then, the distribution characteristics of wind speed in the wind turbine are studied based on three aspects: space, time and dynamic change. After that, a wind speed model is put forward. Application results in an actual wind farm show that the proposed method is effective.

wind power forecasting; dynamic spatial and temporal distribution characteristic; local effect; NWP

10.3969/j.ISSN.1672-0792.2017.04.004

2017-02-20。

TM614

A

1672-0792(2017)04-0020-06

栗梦迪(1996-)，女，本科，研究方向为新能源并网技术、电力系统自动化。