Parzen窗确定系数的协同模糊C均值算法

赵慧珍，刘付显，李龙跃

(空军工程大学 防空反导学院，陕西 西安 710051)

Parzen窗确定系数的协同模糊C均值算法

赵慧珍，刘付显，李龙跃

(空军工程大学 防空反导学院，陕西 西安 710051)

协同模糊C均值(collaboration fuzzy C-means，CFC)算法的协同系数通常根据经验人工设定，且在协同过程中保持不变，不能充分利用数据子集之间的协同关系，算法精度有限。提出Parzen窗确定系数的协同模糊C均值(βp-CFC)算法。用模糊C均值(fuzzy C-means，FCM)算法求出各数据子集的隶属度和聚类中心，再用Parzen窗求出各子集在聚类中心处的密度，根据子集间密度的相关性设定变化的协同系数，利用变化的协同系数进行协同聚类。以Matlab为平台，对βp-CFC算法进行了实验，算法聚类准确率可达到80.34%，比模糊C均值算法、固定系数的CFC算法的准确率分别高出11.80%和3.94%。实验证明，βp-CFC算法较为合理，聚类性能较好。

Parzen窗；密度；模糊C均值；协同系数

0 引 言

聚类算法是数据挖掘领域的重要数据分析方法之一，其原理是利用数据集中对象的相似性形成有限个簇，簇间对象相似性尽可能低，簇内对象相似性尽可能高[1]。常用相似性度量指标有欧式距离、马氏距离、切比雪夫距离等。众多聚类算法中，模糊C均值[2-3](fuzzy C-Means, FCM)算法作为对经典C均值算法的扩展[4]，在数据挖掘、模式识别等领域有着广泛研究和应用。

协同模糊聚类最早在文献[5]中提出，算法利用同一对象在不同数据子集中的信息，即数据子集之间的协同作用，得到更精确的隶属度矩阵，从而提高聚类性能。协同模糊C均值(collaborative fuzzy C-means, CFC)[5-6]算法是在FCM[7]的基础上提出来的，是关于协同模糊聚类最先进的方法之一。如何合理地对数据子集之间的协同关系进行量化，并以协同系数的方式表现出来是CFC算法的关键[8-9]。通常协同系数根据经验人工设定，且在整个协同过程中保持不变，不能充分描述数据子集之间的协同关系[10-11]。针对这种情况，本文提出Parzen窗确定系数的协同模糊C均值(βp-CFC)算法。首先，利用FCM求出各数据子集的隶属度矩阵和聚类中心；其次，利用Parzen窗求出各数据子集在聚类中心处的密度；再其次，根据子集间密度的相关性设定变化的协同系数；最后，用变化的协同系数进行协同聚类。变化的协同系数能够更加充分地描述数据子集之间的协同关系，从而提高聚类精确度。

1 Parzen窗与协同模糊C均值算法

1.1 Parzen窗密度估计

Parzen窗密度估计是一种非参数估计方法，能够很好地利用一组样本对总体概率密度进行估计，从而描述一维或者多维数据的分布状态[1]。以方窗为例，窗函数定义为

(1)

(1)式中，μj为第j维的坐标，当|μj|<0.5(j=1,2,3,…,d)时，窗函数φ(μ)值取1，否则取0。易知，φ(μ)是以原点为中心、以1为边长的的超立方体。落入超立方体内的样本数为

(2)

(2)式中：xi为样本点；x为待估计密度处；hN为方窗窗宽。根据落入窗内的样本点，估计样本在x处的密度为

(3)

(3)式中：N为样本总数；VN为方窗体积。(3)式为Parzen窗概率密度估计的基本公式。Parzen窗有多种核函数，只需满足条件

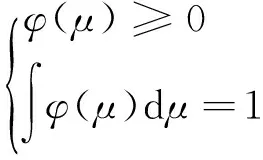
(4)

本文所用核函数为描述正态窗的高斯函数，表示为

(5)

1.2 协同模糊C均值算法

假设数据集X含有N个对象X={x1,…,xN}，任一对象xj为d维向量，代表着d个特征，即xj=[xj1,…,xjd]T∈Rd，利用FCM算法将其聚为c类，则需要目标函数J取得最小值[12-14]，表示为

‖xj-vi‖2

(6)

(6)式中：m是模糊指数，表示隶属度的模糊程度，通常取m=2；xj(j=1,…,N)为待聚类的对象；vi=[vi1,…,vid]T∈Rd(i=1,2,…,c)为第i个聚类中心；‖xj-vi‖为对象与聚类中心之间的距离范数，通常采用欧式距离；uij为隶属度矩阵元素，代表第j个对象属于第i个聚类的程度，隶属度矩阵U的表现形式及其元素uij需满足的约束条件为

U=[uij]c×N

(7)

最优化隶属度矩阵元素urs(r=1,2,…,c;s=1,2,…,N)通过迭代(8)式获得。

(8)

最优化聚类中心vrt(r=1,2,…,c;t=1,2,…,d)通过迭代(9)式获得。

(9)

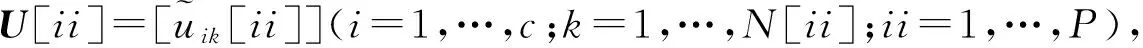
(10)

(11)

(12)

CFC算法能够利用数据子集之间的协同关系，提高聚类性能，但算法的协同系数一般根据经验人工设定且保持不变，不能充分描述子集间的协同关系。

2 βp-CFC算法

协同系数β需要反映数据子集之间的协同关系，β越大，协同数据子集对待处理数据子集的影响越大。数据子集由在相同特征集下定义的对象组成，相同特征在不同数据子集中的分布具有一定的密度相似性，密度相似性越高，相互之间的协同影响越大，反之，影响越小。βp-CFC算法基于Parzen窗密度估计原理，分别估计各数据子集在聚类中心处的密度，再根据密度相关性设定变化的协同系数β，密度相似性越高，β越大。

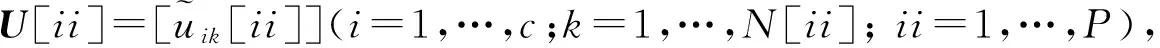
(13)

对于第k个聚类中心vk[ii]，落入以vk[ii]为中心的正态窗内的对象数为

(14)

(14)式中，窗长度hN取值为

(15)

(15)式中：N=N[ii]，N是数据子集中对象的个数；h1为可调节的参数，能够调节窗口大小。根据落入窗内的数据点，估计在vk[ii]处的密度为

(16)

(16)式中，VN为窗的体积。且对于同一数据子集，对象数量N与窗体积VN为固定值。数据子集D[ii]中各聚类的密度函数为

(17)

数据子集D[jj]与D[ii]密度的相关系数为

(18)

(18)式中：cov(P[ii],P[jj])=E[(P[ii]-E(P[ii]))(P[jj]-E(P[jj]))]表示子集P[ii]，P[jj]间的协方差；A[P[ii]]=E(P[ii]-E(P[ii]))2表示子集自身方差。令

K[ii]=[k(v1[ii]),k(v2[ii]),…,k(vc[ii])]T

(19)

则

(20)

简化(18)式得

(21)

由(21)式可知，相关系数可通过计算落入正态窗内的对象个数得到。显然，子集间的相互协同作用越强，相关系数越大，反之，相关系数越小。令

β[ii|jj]=β[jj|ii]=ρ[ii|jj]

(22)

则数据子集D[jj]与D[ii]的相关性越大，二者协同作用越强，协同系数β[ii|jj]越大；子集间相关性越小，协同作用越弱，协同系数β[ii|jj]越小。故协同系数能够充分描述数据子集之间的协同关系。

从图4可见，含钛高炉渣的杂质CaO、MgO、Fe、Al2O3脱除率随着反应时间的延长逐渐增大，但时间超过6 h时，TiO2损失率明显提高，因此，合适的反应时间为6 h。

βp-CFC算法利用变化的协同系数进行聚类，迭代(23)式与(24)式得到隶属度矩阵与聚类中心分别表示为

(23)

(24)

βp-CFC算法的具体步骤如下。

1)拆分数据子集；

2)利用FCM算法计算每个数据子集的隶属度矩阵U[ii]和聚类中心V[ii]；

3)数据子集间类别匹配；

4)根据(21)式计算各子集间相关系数；

5)根据(22)式计算各子集间协同系数β[ii|jj]；

6)分别根据(23)式和(24)式计算协同隶属度矩阵和协同聚类中心；

7) 输出聚类结果。

βp-CFC算法流程如图1所示。

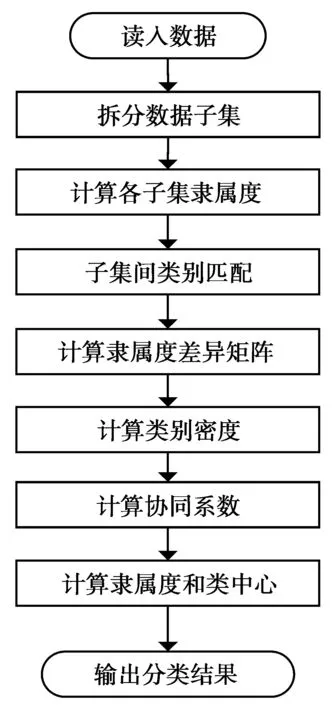
图1 βp-CFC算法流程Fig.1 Flow chart of βK-CFC algorithm

3 实验分析

为验证βp-CFC算法协同系数的有效性及聚类性能，本文进行了2组实验。第1组是聚类准确性分析，利用加州大学(university of California Lrvine, UCI)数据库中的Wine数据集[12-13]，分别以不同且固定的β值和βp-CFC算法得到的变化的β值进行聚类，并将聚类结果与UCI提供的标准结果进行比较；第2组是聚类指标分析，利用人工数据集Dataset，分别以βp-CFC算法和FCM算法进行聚类，并用系数(partition coefficient，PC)，分离熵(classification entropy, CE)，SC指标(partition index，SC)，S指标(separation index，S)，XB 指标(Xie and Beni’s index，XB)，DI指标(Dunn’s index，DI)这6项指标对聚类结果进行评价[14]。

3.1 聚类准确性分析

利用UCI数据库中的真实数据集Wine进行实验。Wine数据集描述了178个对象的13种特征，这些对象可被聚为3类。UCI同时提供了准确的聚类结果用于对比分析。

将数据集拆分为4个数据子集，每个数据子集均由从原始数据中抽取的6组特征组成，如表1所示。

根据第2节所述求得协同系数β，见表2。因为只考虑子集之间的协同作用，故令子集与自身的协同系数为0。

表1 数据子集所包含的特征

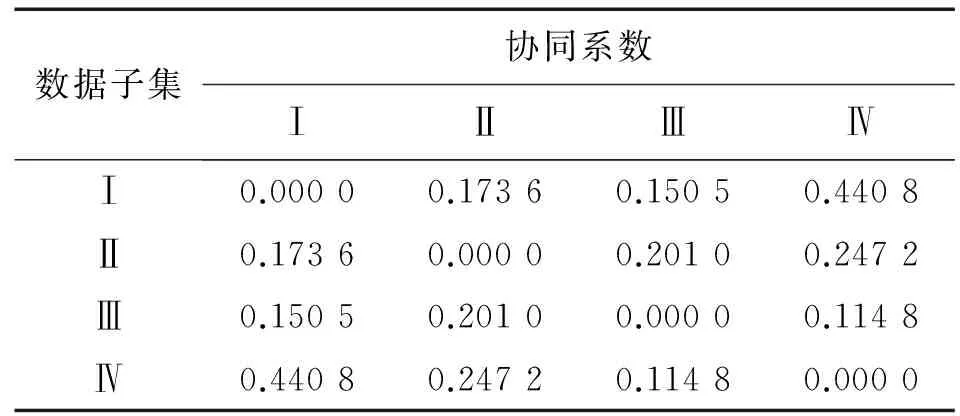
表2 数据子集之间的协同系数

根据协同系数β，迭代(23)式与(24)式，求得隶属度矩阵和聚类中心，判定对象属于隶属度最大的一类，从而聚类。为对比分析，设β分别取固定值0.2，0.4，0.6，0.8，并在同一数据集中进行实验。将5组实验得到的聚类结果与UCI提供的标准聚类比较，得到如表3所示结果。由表3可见，βp-CFC算法得到的聚类正确率最高。当β取不同的固定值时，聚类效果差异较大，但CFC算法总体性能优于FCM算法。

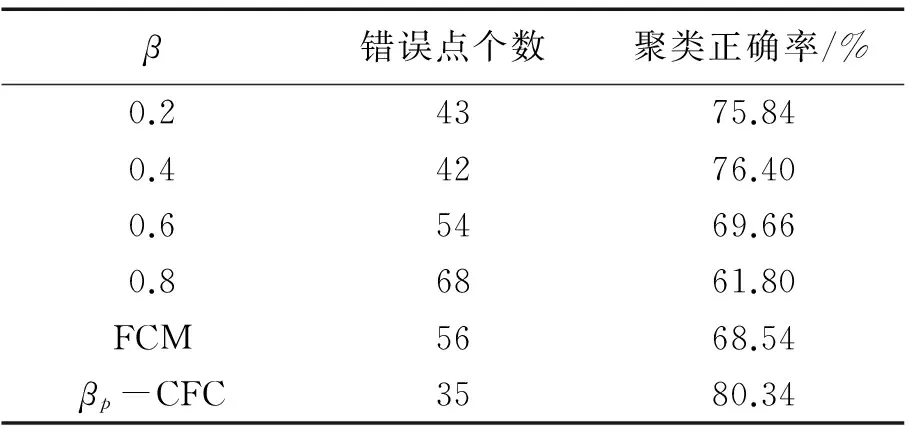
表3 β取不同值时得到的聚类结果

根据特征12和特征13可视化聚类结果。作为对比，UCI提供的标准结果，βp-CFC算法得到的聚类结果及协同系数取固定值0.8时的聚类结果分别如图2—图4所示，其中，图3和图4中的圆圈内的点表示错误聚类的点。显然，与标准结果相比较，固定协同系数得到的聚类错分点较多，本文算法得到的错分点相对较少。

图2 标准聚类Fig.2 Standard clustering result

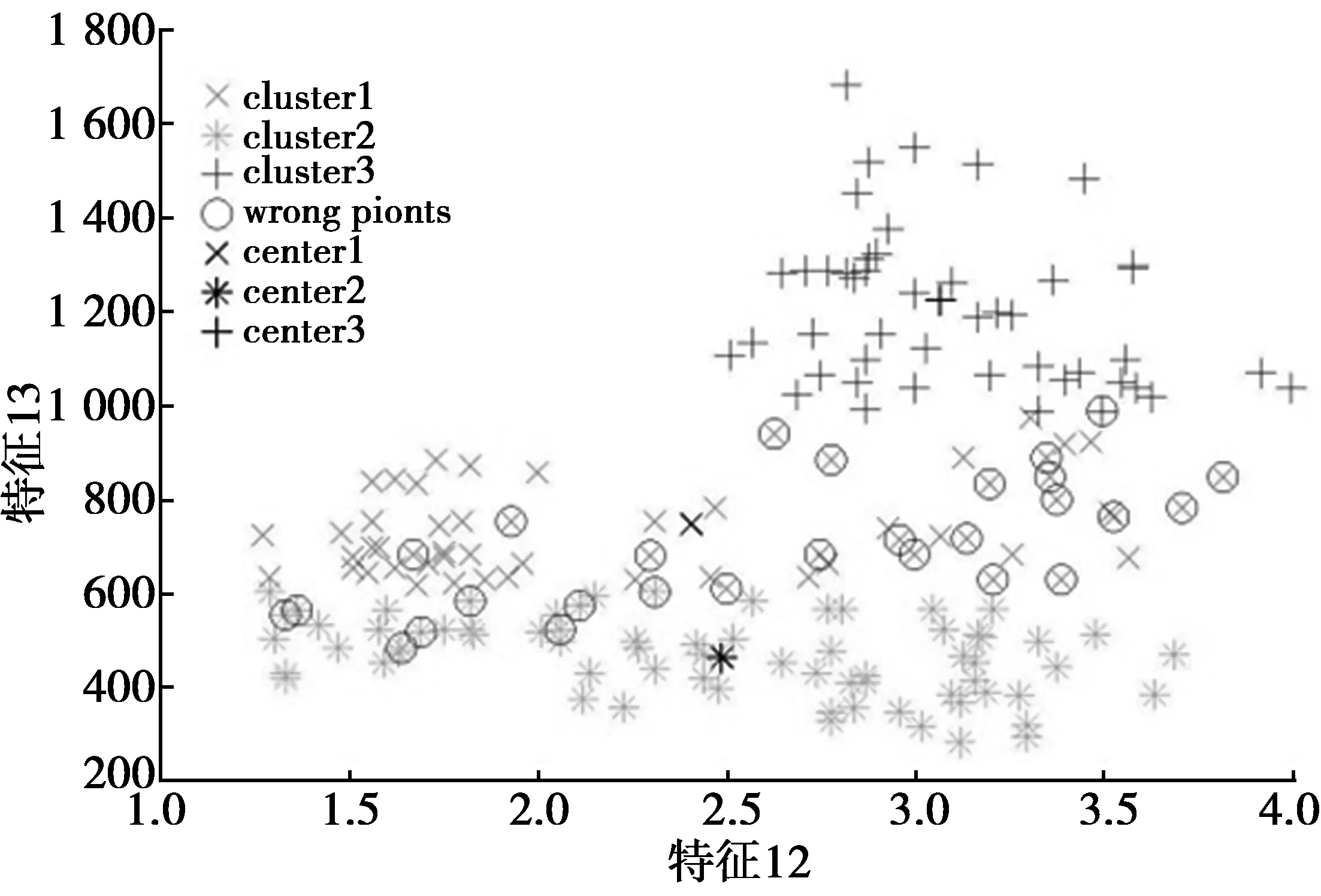
图3 βp-CFC得到的聚类Fig.3 Clustering result gained by βP-CFC

图4 β=0.8时得到的聚类Fig.4 Clustering result when β=0.8

3.2 聚类指标分析

聚类有效性评价方法有多种，本文选取了常用的几种评价方法用于实验[15-16]，从多角度描述聚类结果。

1) PC指标。PC是仅考虑隶属度的聚类有效性指标，如(25)式，其取值为[0,1]。PC指标形式简单，易于计算。

(25)

PC的值越大，意味着聚类性能越好。

2)CE指标。CE也仅度量隶属度信息，如(26)式，其取值为[0,logaC]，并随着聚类数的增加而单调变化。

(26)

CE的值越大，意味着聚类性能越好。

3)SC指标。SC同时考虑了数据集几何结构信息和隶属度信息2个方面，采用紧致性度量和分离性度量的比值形式，如(27)式，其中，紧致性是指类内各样本与聚类中心的距离之和；分离性是指所有聚类中心距离之和。

(27)

SC的值越小，意味着聚类性能越好。

4)S指标。与SC相反，S利用最小距离分离度来衡量隶属度的有效性，表示为

(28)

S的值越小，意味着聚类性能越好。

5)XB 指标。XB也同时考虑了数据集几何结构信息和隶属度信息2个方面，是一个比值型模糊聚类有效性指标，表示为

(29)

XB的值越小，意味着聚类性能越好。

6)DI指标。DI指标考虑了数据集几何结构信息，如(30)式，其最初目的是为了衡量分离性较好的聚类，而这类聚类通常模糊性较小，故DI的衡量过程有些类似硬聚类性能的衡量。

(30)

DI的值越小，意味着聚类性能越好。

文章利用人工数据集Dataset进行实验，数据集共有2 000个对象，6种特征，可被分为3类。对数据集分别利用βp-CFC算法和FCM算法进行实验，并利用上文所述聚类指标进行评价，对比得到如表4所示的结果。表4中评价依据里的“↑”表示指标越大，聚类性能越好；“↓”表示指标越小，聚类性能越好。

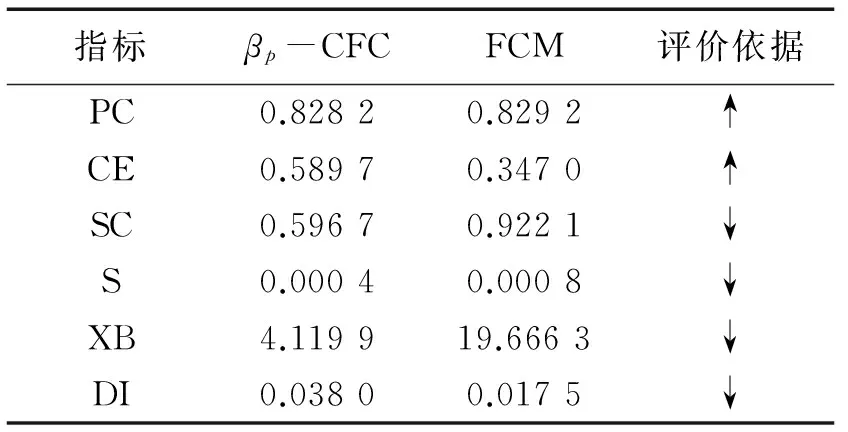
表4 聚类指标

由表4可知，PC，CE，SC，S和XB这5个指标显示，βp-CFC算法不劣于甚至明显优于FCM算法。这5种指标均考虑的是聚类几何结构信息和隶属度信息中的1个方面甚至2个方面，而文中模糊协同聚类是根据点间距离，即聚类几何结构信息得到的隶属度信息进行划分的，显然βp-CFC算法优于FCM算法。DI指标虽然考虑了数据集的几何结构信息，但其最初目的是为了衡量分离性较好的聚类，而这类聚类通常模糊性较小，故DI的衡量过程有些类似硬聚类性能的衡量，βp-CFC算法根据数据子集之间的协同性进一步描述数据的模糊性，故在DI指标上βp-CFC算法性能略逊于FCM算法。总体而言，βp-CFC算法优于FCM算法。

4 结 论

本文利用Parzen窗密度估计算法，分别估计各数据子集的密度，根据密度相关性得到变化的协同系数β，且密度相似性越高，β值越大，能够充分描述数据子集之间的协同关系，提高协同聚类算法的性能。

[1] 边肇祺,张学工.模式识别[M]. 3版. 北京：清华大学出版社，2010：274-295. BIAN Z Q, ZHANG X G. Pattern Recognition[M]. 3rd ed.Beijing: Press of Tsinghua University,2010:274-295.

[2] BEZDEk J C.Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Press,1981.

[3] 杨漫，苏亚坤．采用模糊C-均值聚类的自适应图像分割算法[J]．重庆理工大学学报：自然科学版，2015，29(6):94-99． YANG Man，SU Yakun．Adaptive Algorithm Based on Fuzzy C-Means for Image Segmentaion[J]．Journal of Chongqing University of Technology：Natural Science Edition，2015，29(6):94-99．

[4] JAIN A K. Data clustering: 50 years beyond K-means[J].Pattern Recognition Letters,2010,31(8):651-666.

[5] PEDRYCZ Witold.Collaborative fuzzy clustering[J].Pattern Recognition Letters, 2002,23(14):1675-1686.

[6] PEDRYCZ W, RAI P. Collaborative clustering with the use of fuzzy C-means and its quantification [J]. Fuzzy Sets and Systems, 2008,159(18): 2399-2427.

[7] COLETTA L F S.Collaborative fuzzy clustering algorithms: some refinements and design guidelines[J].IEEE Transactions on Fuzzy Systems, 2012, 20(3):444-462.

[8] 孙延维,彭智明,李健波. 基于粒子群优化与模糊聚类的社区发现算法[J]. 重庆邮电大学学报：自然科学版,2015,27(5):660-666. SUN Yanwei, PENG Zhiming, LI Jianbo. Community detection algorithm based on particle swarm optimization and fuzzy clustering [J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2015,27(5):660-666.

[9] ZARINBAL M,ZARANDI M H F, TURKSEN I B.Relative entropy collaborative fuzzy clustering method[J].Pattern Recognition,2014,8(3):338-353.

[10] PATERLINI S,KRINK T.Differential evolution and particle swarm optimization in partitional clustering[J]. Computational Statistics and Data Anlysis, 2006,50(5):1220-1247.

[11] 高翠芳,黄珊维,沈莞蔷,等. 基于信息熵加权的协同聚类改进算法[J]. 计算机应用研究,2015,32(4):1016-1018，1023. GAO Cuifang,HUANG Shanwei,SHEN Wanqiang, et al. Improved collaborative clustering algorithm based on entropy weight[J]. Application Research of Computers, 2015,32(4): 1016-1018，1023.

[12] KARTHI R, ARUMUGAM S, RAMESHKUMAR K. Comparative evaluation of particle swarm optimization algorithms for data clustering using real world data sets[J]. IJCSNS International Journal of Computer Science and Network Security, 2008,8(1):203-212.

[13] 毛韶阳,李肯立.K-means初始聚类中心优化算法研究[J].重庆邮电大学学报：自然科学版,2007,19(4):422-425. MAO Shaoyang, LI Kenli. Research on K-means initial clustering center optimal algorithm[J]. Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2007, 19(4):422-425.

[14] 陈小辉,张功萱. 基于信息熵的符号属性精确赋权聚类方法[J]. 重庆邮电大学学报：自然科学版,2014,26(6):850-855. CHEN Xiaohui, ZHANG Gongxuan.Symbol property accurate weight clustering method based on information entropy[J].Journal of Chongqing University of Posts and Telecommunications ：Natural Science Edition, 2014,26(6):850-855.

[15] 符保龙, 张爱科. 基于均值密度中心估计的k-means聚类文本挖掘方法[J]. 重庆邮电大学学报：自然科学版, 2014, 26(1): 111-115. FU Baolong, ZHANG Aike. K-means clustering text mining method using center estimation based on mean density[J]. Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2014, 26(1): 111-115.

[16] 周开乐,杨善林,丁帅,罗贺.聚类有效性研究综述[J].系统工程理论与实践,2014,34(9):2417-2431. ZHOU Kaile, YANG Shanlin, DING Shuai, et al. On cluster validation[J].Systems Engineering-Theory & Practice, 2014,34(9):2417-2431.

(编辑：王敏琦)

Novel collaboration fuzzy C-means algorithm with Parzen window determined collaboration coefficient

ZHAO Huizhen, LIU Fuxian, LI Longyue

(School of Air and Missile Defense, Air Force Engineering University, Xi’an 710051, P.R.China)

Collaboration fuzzy C-means algorithm (CFC) can improve the performance of fuzzy C-means algorithm by using the collaborative relationship between the sub data sets. But the collaboration coefficient of CFC, in an inadequate using of the collaborative relationship, is always determined by priori knowledge and remains constant during collaboration stages. In order to circumvent this limitation, a novel collaboration fuzzy C-means algorithm with Parzen window determined collaboration coefficient(βp-CFC) was developed. First, fuzzy partition matrix and cluster prototypes of every sub data sets are computed by fuzzy C-means algorithm (FCM)，for the further computing of collaboration coefficient. Second, density of the cluster prototypes is gained by Parzen window method. Third, collaborative coefficient is dynamically adjusted by the correlation of density. Last, objects are clustered with dynamical collaborative coefficient. The algorithm is tested on the matlab platform, achieving a high accuracy of 80.34%, higher than FCM and CFC with 11.80% and 3.94%, respectively. Examples are provided to demonstrate the rationality of collaboration coefficient and the better performance of CFC.

Parzen window；density；fuzzy C-means algorithm；collaborative coefficient

10.3979/j.issn.1673-825X.2017.02.020

2016-01-21

2016-10-12 通讯作者：赵慧珍 happy100zhao90@163.com

TP391.3

A

1673-825X(2017)02-0272-07

赵慧珍(1990-),女，山东单县人，博士研究生，主要研究方向为数据挖掘。E-mail:happy100zhao90@163.com。