基于特征滤波法的滤波器组优化设计

宋 锐

(中国电子科技集团公司第20研究所 雷达部, 陕西 西安 710068)

基于特征滤波法的滤波器组优化设计

宋 锐

(中国电子科技集团公司第20研究所 雷达部, 陕西 西安 710068)

动目标检测(MTD)是现代雷达信号处理领域的一项重要技术，而对MTD的性能起决定性作用的是多普勒滤波器组的设计。相对传统采用快速傅里叶变换(FFT)方法设计的MTD的缺点，希望设计出一组在零频处抑制比达60 dB，对动杂波抑制比达50 dB的一组滤波器。文中采用特征滤波器法设计得到了一组滤波器系数，并经过简要仿真验证，用该方法得到的滤波器组较传统FFT法设计的滤波器组性能要优越，在某些性能上也优于加窗FFT法。

MTD；特征滤波器；抑制比

动目标检测(Moving Target Detention，MTD)[1]是现代雷达信号处理领域一项重要的技术，通过对回波脉冲作相参积累实现匹配滤波，使得信噪比得到改善，在复杂背景中检测目标的能力得到提高[2]。多普勒滤波器组的设计是MTD系统的核心，其性能决定了MTD的性能，其实现通常采用快速傅里叶变换(FFT)方法和有限冲激响应(FIR)横向滤波器两种方法[3-5]，前者方法灵活性较差，且杂波可能通过较高的副瓣(-13.2 dB)进入而导致改善因子的下降，且对低速目标的检测性能较差；而FIR滤波器具有灵活性，设计出的滤波器可得到较好的MTD效果[6]。本文提出一种基于特征滤波器法设计的多普勒滤波器组，其每个滤波器在零频都有比较深的凹口，而且副瓣也比较低，可以得到较大的信杂比改善，可以克服FFT法的一些缺点。

1 MTD滤波器设计

雷达探测的回波信号不仅包含有目标的回波信息，而且还包含了地杂波，气象杂波和箔条干扰等杂波信号[7]，基于目标与(静速或者运动)杂波速度的区别，这一速度差别反映在雷达回波的多普勒频率上，所以可以采用一组带通滤波器对回波信号进行滤波处理，再对滤波器的输出进行检测来发现目标[8-9]。

鉴于FFT法的滤波器不足，希望设计一组副瓣低，且每个非零滤波器在零频要有较深凹口的滤波器组，设计思想是将0 ～ 2π的频率范围分为N段，每一段作为一个滤波器的通带。将零频附近的地杂波区设为第一阻带，除通带与第一阻带以外的区域设为第二阻带和第三阻带，用于抑制运动杂波。其中通带与第一阻带的幅度比要大于雷达对固定杂波信杂比改善量的要求，而通带与第二，三阻带的幅度比要大于雷达对运动杂波信杂比改善量的要求[10]。

图1 多普勒滤波器的设计要求

本文采用的特征滤波器法[2-3]是通过求解目标函数式(1)，使其值最小的方法来获取所需的滤波器系数

E=α1Ep1+α2Ep2+…+αkEpk+β1ES1+
β2ES2+…+βLESL

(1)

式(1)中，K代表通带数和L代表阻带数；αi(i=1，2，…，K)和βi(i=1，2，…，L)分别是各通带与阻带的权值系数；Epi(i=1，2，…，K)和ESi(i=1，2，…，L)分别是通带与阻带的误差函数且

(2)

(3)

式(2)和式(3)中，ωpu，ωpl是通带的带限；ωsu，ωsl是阻带的带限；D(ω)，H(ω)分别是所期望的幅频响应函数，所设计的幅频响应函数，ω0选择在|D(ω)|最大值的频率处[11]。

假设所设计的幅频响应函数

(4)

式中，N为滤波器长度，h(n)是滤波器系数。

定义A=[h(0),h(1),…,h(N-1)]T以及C(ω)=[1,e-jω,…,e-j(N-1)ω]T，式(4)可以重新写为

H(ω)=ATC(ω)=CT(ω)A

(5)

将式(5)分别带入式(2)和式(3)中，经化简分别得到

Ep=AHQpA

(6)

ES=AHQSA

(7)

式(6)和式(7)中

(8)

(9)

将式(6)～式(9)带入目标函数式(1)得

E=AH[α1QP1+…+αKQPK+β1QS1+…+βLQSL]A=
AHQA

(10)

对于滤波器的设计要求，经多次实验验证，对于权值系数定义为

(11)

式中，SCR1是雷达对固定杂波信杂比改善量的要求；SCR2是雷达对运动杂波信杂比改善量的要求；ws11，ws12为第一阻带的阻带截止频率；ws21，ws22为第二阻带的阻带截止频率；ws31，ws32为第三阻带的阻带截止频率；ws41，ws42为第四阻带的阻带截止频率；deta自定义为第一阻带与第二阻带之间的抑制量差。式(10)中矩阵Q的最小特征值对应的特征向量就是所要设计的滤波器系数[12-13]。

以下是在频率[0 ，2π]范围内根据此方法设计出一组16阶的滤波器组的效果图。

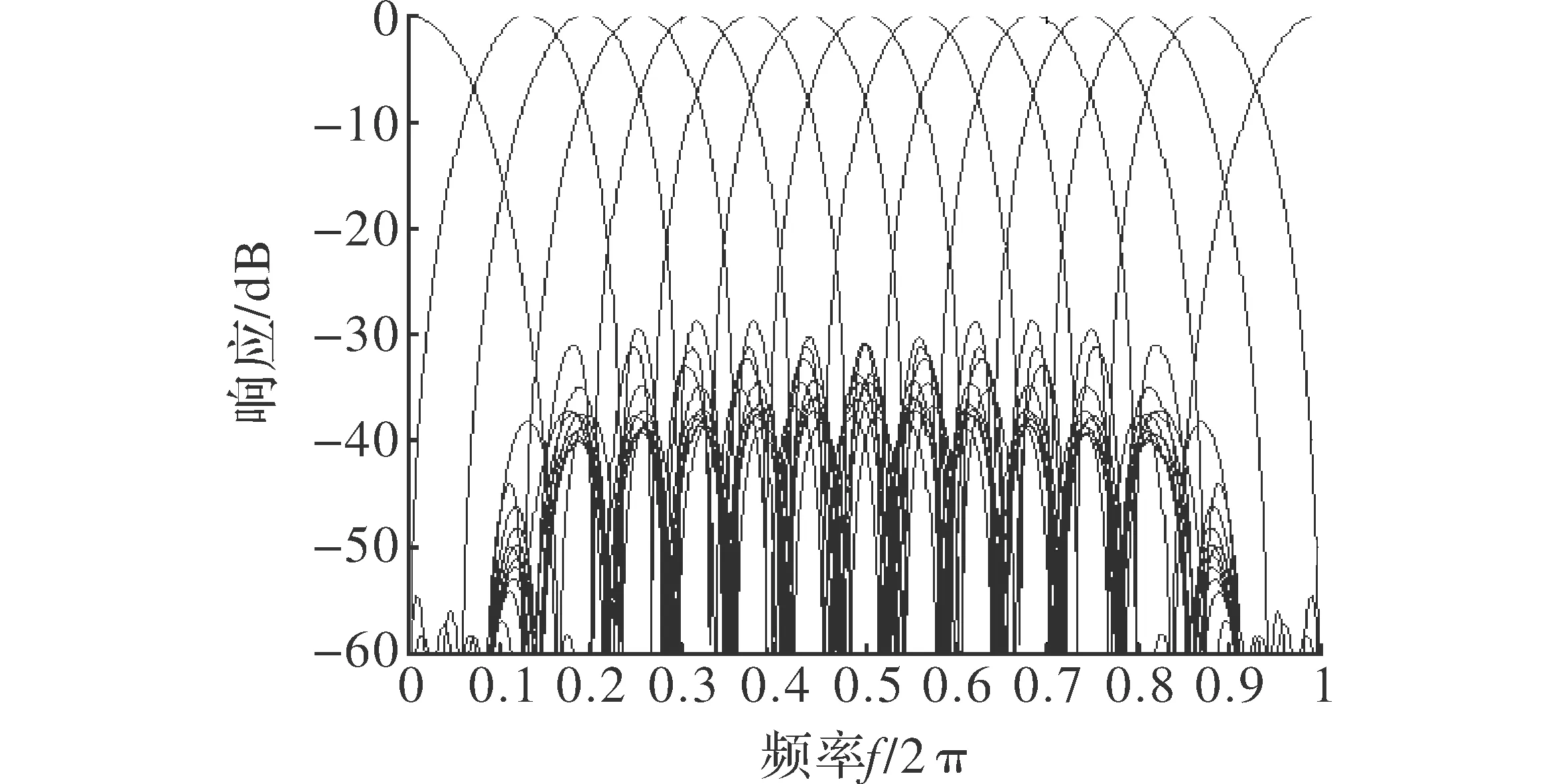
图2 15个16阶滤波器组

图3 0号滤波器

图5 7号滤波器

从图2可以看出，每个滤波器均匀的分布在频率[0,2π]范围内，且每个非零滤波器在零频附近都有很深的凹口(>-50 dB)，所以对地杂波的改善因子可达50 dB以上；其第二，三阻带也基本达到-30 dB，对运动杂波有较好的抑制作用；由图4可知1号滤波器在零频附近的凹口达到-20 dB以上，对于低速目标的检测效果好点；对于存在于零频附近的目标，则可通过建立杂波图来作为0号滤波器的门限，可用于检测超过杂波的强目标回波[14-15]。

2 仿真验证并与FFT作分析比较

为了验证所设计的多普勒滤波器组的MTD处理效果，用Matlab进行仿真验证。仿真参数：雷达波长λ=0.191 1 m；PRT=240 μs；采样率fs=2 MHz；脉冲数为16。假设有4个目标，且对应的距离分别为3 000 m，14 000 m，14 000 m，20 200 m，速度分别为40 m/s，90 m/s，180 m/s，336 m/s；其信噪比分别为40 dB，30 dB，33 dB，30 dB。假设有静杂波和动杂波(动杂波的速度为2.5m/s)，杂噪比分别为30 dB，35 dB，分别位于距离单元[0∶2∶38]和[250∶2∶258]，静杂波的谱宽为20 Hz。

图6 未加窗的FFT法MTD

图7 加窗的FFT法MTD

图8 优化设计MTD

结果分析：已知距离分辨力为C/(2×Fs)=75 m,有Matlab仿真结果3种方法测得的目标所在的距离门均为40 m，186 m，269 m，对应距离为3 000 m，13 950 m，20 175 m；与仿真条件给出的值在误差范围(±75 m)之内。对于16点MTD，每个多普勒通道对应的速度为24.88 m/s；而对于15点MTD，每个多普勒通道对应的速度为26.54 m/s；由Matlab仿真结果可知，加窗与未加窗方法由于频谱扩展和滤波效果差，而无法准确测出各目标的速度；优化MTD法测得目标所在的多普勒通道为1，3，7，13，对应计算的速度为26.54 m/s，79.62 m/s，185.78 m/s，345.02 m/s；由图6～图8可知优化MTD在杂波抑制和目标检测方面都优于未加窗和加窗MTD。由Matlab测量结果可以看出，在误差范围内其测距，测速基本准确。特别是测量同一距离内目标的速度时，优化的MTD较其他两种效果都好，总结3种方法的优缺点如表1所示。

表1 3种方法之间的对比关系

3 结束语

本文介绍了一种利用基于特征滤波器法设计的多普勒滤波器组对雷达回波信号进行滤波处理，对杂波的抑制能力以及对弱目标的检测能力方面有了较大改善，但滤波效果的好坏与所设计的滤波器组有关；从运算量来看，FFT法处理时可以直接调用库函数，比较简便，采用优化设计的多普勒滤波器组，需要根据雷达工作重频设计每个滤波器，因此比较复杂，但却能获得更好的滤波效果。

[1] 耿富录.雷达原理[M].西安:西安电子科技大学出版社,2006.

[2] 张明友,汪学刚.雷达系统[M].北京:电子工业出版社,2006.

[3] 陶海红.雷达信号处理机几个关键技术研究[D].西安:西安电子科技大学,2002.

[4] 陈伯孝.现代雷达系统分析与设计[M].西安:西安电子科技大学出版社,2006.

[5] 邢孟道,王彤,李真芳.雷达信号处理基础[M].北京:电子工业出版社,2008.

[6] 贾可新,柳桃荣.一种基于最大信杂比的MTD滤波器设计算法[J].雷达科学与技术,2014(5):506-509.

[7] 朱先正.雷达杂波研究及模拟[D].南京:南京理工大学,2006.

[8] 汪莉君.雷达杂波抑制技术的研究[D].西安:西安电子科技大学,2005.

[9] 宗爱华.雷达MTI/MTD杂波抑制技术研究[D].武汉:湖北大学,2012.

[10] 吴顺君,梅晓春.雷达信号处理和数据处理技术[M].北京:电子工业出版社,2010.

[11] Pei S C,Shuyu J J.Eigenfiter design of higher order digital differentiators[J].IEEE Transactions on Acoust, Speech,Signal Processing,2009(4):152-158.

[12] Truong Q Nguyen.The design of arbitrary FIR digital filters using the eigenfilter method[J].IEEE Transactions on Circuit,2013,41(4):87-92.

[13] Pei Soo Chang,Shyu Jong-Jy.Complex eigenfilter design of arbitrary complex coefficient FIR digital filters[J].IEEE Transactions on Circuit,2012,40(1):99-103.

[14] 周亚飞,赵修斌,邹鲲.FFT-MTD滤波器组优化设计与仿真[J].现代防御技术,2011(2):160-163,175.

[15] 谷泓,赵永波,张守宏.一种基于数字综合算法的MTD滤波器设计方法[J].航空计算技术,2002,32(2):58-62.

Optimal Filter Bank Design Based on Feature Filtering

SONG Rui

(Radar Division, 20th Research Institute of China Electronics Technology Group Corporation, Xi’an 710068, China)

Moving target detection (MTD) is an important technology in the field of radar signal processing, and the performance of MTD plays a decisive role in the design of Doppler filter banks. Considerting the shortcomings of the traditional Fast Fourier Transform (FFT) design of MTD, we design a set of filter with a rejection ratio of 60dB at zero frequency and 50dB to dynamic clutter rejection ratio. In this paper, a set of filter coefficients are designed by using the characteristic filter method. A brief simulation shows that the filter banks obtained by this method are superior in performance to those by the conventional FFT method, and are also superior in some aspect to the Windowed FFT method.

MTD; characteristic filter; inhibition ratio

2016- 01- 24

国家自然科学基金(61671361)

宋锐(1988-)，男，硕士，助理工程师。研究方向：雷达信号处理。

10.16180/j.cnki.issn1007-7820.2017.05.016

TN957.51

A

1007-7820(2017)05-058-04