基于ARIMA-GARCH-t与ELM的人民币汇率组合预测模型研究①
姬 喆
(聊城大学商学院,山东聊城252059)
基于ARIMA-GARCH-t与ELM的人民币汇率组合预测模型研究①
姬 喆
(聊城大学商学院,山东聊城252059)
本文旨在对人民币汇率进行预测,以丰富汇率预测方法、方式.利用2012年1月4日到2014年11月3日的人民币对美元汇率中间价数据,依据组合预测方差最小原则构建ARIMA-GARCH-t与ELM(极限学习机)组合预测模型来分析人民币汇率的非线性时间序列特征,该模型一方面弥补了ARIMA预测时残差异方差性对预测精度的影响,同时将随机扰动项对模型的影响考虑在内,另一方面发挥ELM学习速度快、泛化性能好等特点.实例分析证明,该组合预测模型预测精度高于单一预测方法,是一种有效的预测方法.
汇率,ARIMA-GARCH-t模型,ELM,组合预测模型
0 引言
随着中国经济的发展以及人民币加入SDR,人民币在国际货币中的重要地位越来越突显,其对宏观经济运行以及微观经济的资源配置具有重要影响.因此,准确预测、分析人民币汇率对金融政策与投资政策的制定具有重要意义[1].
人民币汇率是一个受到各种因素影响的非线性动力系统,而人民币汇率预测应用时间序列进行测算[2].传统的汇率预测方法有神经网络、灰色模型、ARIMA模型等.神经网络作为一种新的时间序列预测方法,表现出很高的预测精度[3],但神经网络存在训练速度慢、易陷入局部极小、初始值选择敏感等缺点[4],灰色预测模型具有所需数据少、样本简单、精确性较高的特点[5],需要保证原始数据为光滑离散数列,但即使满足条件利用灰色模型也能导致较大的误差,熊刚、陈章潮提出的利用较小的值代替指数a的方法较为复杂,不宜推广[6].
ARIMA模型是从时间序列自身出发建立模型,线性拟合能力较好[7],但该模型只能对残差具有方差齐性的时间序列进行预测,对有异方差的时间序列会增大预测误差.极限学习机(ELM)无需调整输入层与隐含层的连接权值及隐含层神经元的阀值,只需设置隐含层神经元的个数,便可获得唯一解.与传统训练方法(BP、RBP等)相比,极限学习机具有强大泛化能力以及较快的学习速度[8],通过一步矩阵运算即可得出隐藏层与输出层的链接权重,具有学习速度快的优点,提高了算法的训练速度[9].
基于此,本文构建ARIMA-GARCH-t与ELM组合预测模型对人民币汇率进行预测,该组合模型既发挥了ARIMA-GARCH-t模型对残差异方差性、非线性数据处理能力[10],同时充分考虑了随机扰动项对误差的影响,又发挥了极限学习机泛化能力强、学习速度快的优点.人民币汇率实例表明,该预测模型简单可行且具有较高的预测精度.
1 人民币汇率组合预测模型建立
ARIMA(p,d,q)模型又称求和自回归移动平均模型
(1)
使用ARIMA对非平稳序列进行拟合时需要保证残差数列为零均值的白噪声序列,且当残差存在异方差时尝试使用GARCH(p,q)模型[12],其完整结构如
(2)
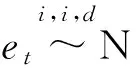
1.2 极限学习机原理
极限学习机是由南洋理工大学黄广斌副教授于2004年提出的一个针对单隐含层前馈神经网络的新算法[13].该算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阀值,克服了传统SLFN采用梯度下降法需要多次迭代以达到修正权值和阀值的目的局限.极限学习机无需设置所有网络训练参数,只需要设置隐含层神经元的个数,便可以得到唯一最优解.
设具有Q个样本的训练输入矩阵X和输出矩阵Y分别为
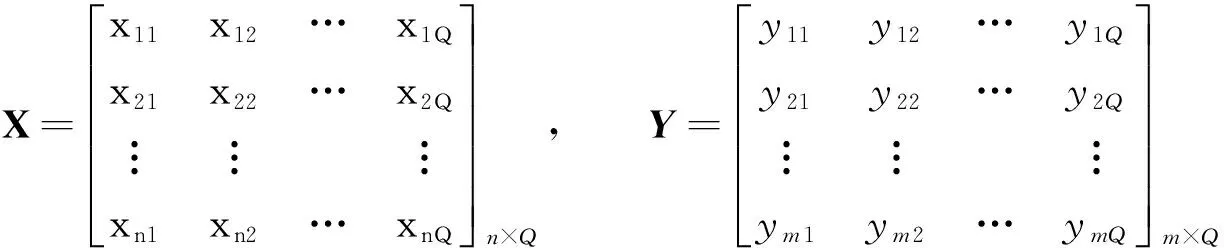
则具有M个隐层节点的标准SLFN为
最近几年,由于在保护地连续多年种植茄科类作物使得土壤中致病菌数量不断积累,茄子病虫害严重发生。在育苗过程中,将茄子幼苗嫁接在其他砧木上能够有效减少茄子自身携带的土传病害,避免茄子在后期种植过程中出现严重的病虫害。
T=[t1,t2,…,tQ]m×Q,
(3)
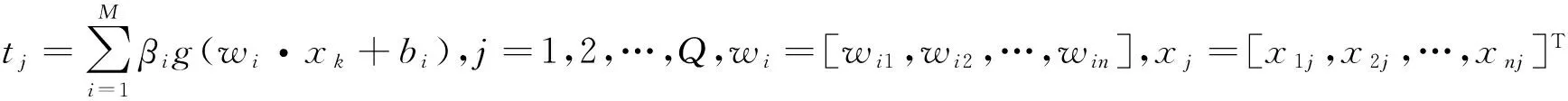


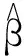
1.3 组合预测模型原理
本文通过确定合理的权数,建立ARIMA-GARCH-t与ELM模型的组合预测模型.组合预测模型形式如[14]
W1y1t+W2y2t,
(4)
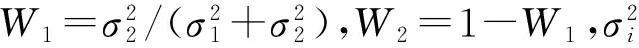
1.4 组合预测模型建模步骤

图1 组合预测建模步骤
首先,对数据进行平稳性检验,ADF检验得出序列是非平稳的,通过差分法使序列变为平稳序列,再对该平稳序列进行白噪声检验,检验通过则分析结束,否则再尝试建立ARIMA模型检验其残差方差齐次性,若为非齐性则尝试建立ARIMA-GARCH模型,充分考虑随机扰动项对模型的影响,建立ARIMA-GARCH-t模型,然后将ARIMA-GARCH-t模型与ELM模型融合,建立组合预测模型,并对人民汇率进行预测,建模步骤如图1所示.
2 实例分析
2.1 ARIMA-GARCH-t模型建立
美元兑人民币汇率数据来源于中国外汇交易中心(2012年1月4日至2014年11月3日).软件利用Eviews6.0得到图2到图3结果.图2美元兑人民币汇率递减初步判断出时间序列非平稳,图3显示出该时间序列出现明显的自相关性,即时间序列为非平稳的.

图2 人民币汇率时序图与自相关、偏自相关图
对时间序列进行一次差分,由图3可以看到时间序列一阶差分后在0附近波动,无明显单调、周期趋势,初步判断一阶差分时间序列为平稳的,由ADF检验得出一阶差分时间序列是平稳序列.由自相关偏自相关图可以尝试建立ARIMA(4,1,4)模型、ARIMA(3,1,3)模型,通过检验如表1发现ARIMA(3,1,3)符合要求.ARIMA(4,1,4)中AR(2),AR(3),MA(2)不合要求,剔除建立疏松系数模型ARIMA((1,3),1,(1,3,4)),通过施瓦兹准则SC与赤池信息量准则AIC,选取取值较小的ARIMA((1,3),1,(1,3,4).

图3 一阶差分时序图与自相关、偏自相关图

变量相关系数标准误差t检验p值AR(1)-0.4466560.217282-2.0556520.0402AR(3)0.4342960.1778342.4421380.0149MA(1)0.4701390.2192632.1441770.0324MA(3)-0.4771630.178402-2.6746490.0077MA(4)-0.0791190.0386182.0487250.0409
表2 ARCH效应检验

统计检验统计量p值F检验24.417020.00001LM检验23.636660.00001
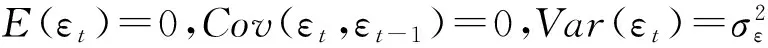
2.2 ELM模型建立
首先利用ELM学习算法对训练样本进行试验,然后根据效果检验指标MSE(均方误差)并选取最佳的网络,最后利用选取的网络处理样本数据,对汇率进行预测.网络的训练效果可由MSE大小进行判断,选取MSE较小的网络用于汇率预测.经过多次的试验,与用预测同期前一个月、前三个月、前半年和前一年的汇率来预测当前汇率相比用预测日期前十天的汇率来预测当天的汇率可以取得很好的效果.MSE比较如表3所示.
表3 MSE结果比较

时间长度MSE十天1.007e-5一个月0.2653三个月0.3572半年0.3683一年0.3475

图4 测试集预测结果对比
从2012年1月4日起取十天的汇率中间价作为网络输入参数,第十一天的汇率值作为输出形成一条样本,以此类推取出674条样本,选取640条样本作为训练样本,34条样本作为测试样本.经样本训练,ELM隐含层神经元个数为20,活化函数为‘sig’函数.结果如图4所示,ELM的MSE较小,证明其具有较好的预测效果、具有较高的精度.
2.3 组合模型建立与比较
根据公式(4)建立ARIMA-GARCH-t与ELM的组合预测模型,w1=0.501 5,w2=0.498 5,y0t=0.501 5y1t+0.498 5y2t,y1t、y2t分别为ARIMA-GARCH模型与ELM的预测值.表4给出2014年9月10日-11月3日的5天预测值与真实值比较的部分数据,通过表4可以看到组合预测模型的相对误差比ARIAM-GARCH-t模型与ELM模型要低.由表5可以看到,组合预测模型的MSE,SDE,MAPE均低于ARIAM-GARCH-t模型与ELM模型,即组合预测模型的精度更高一些.
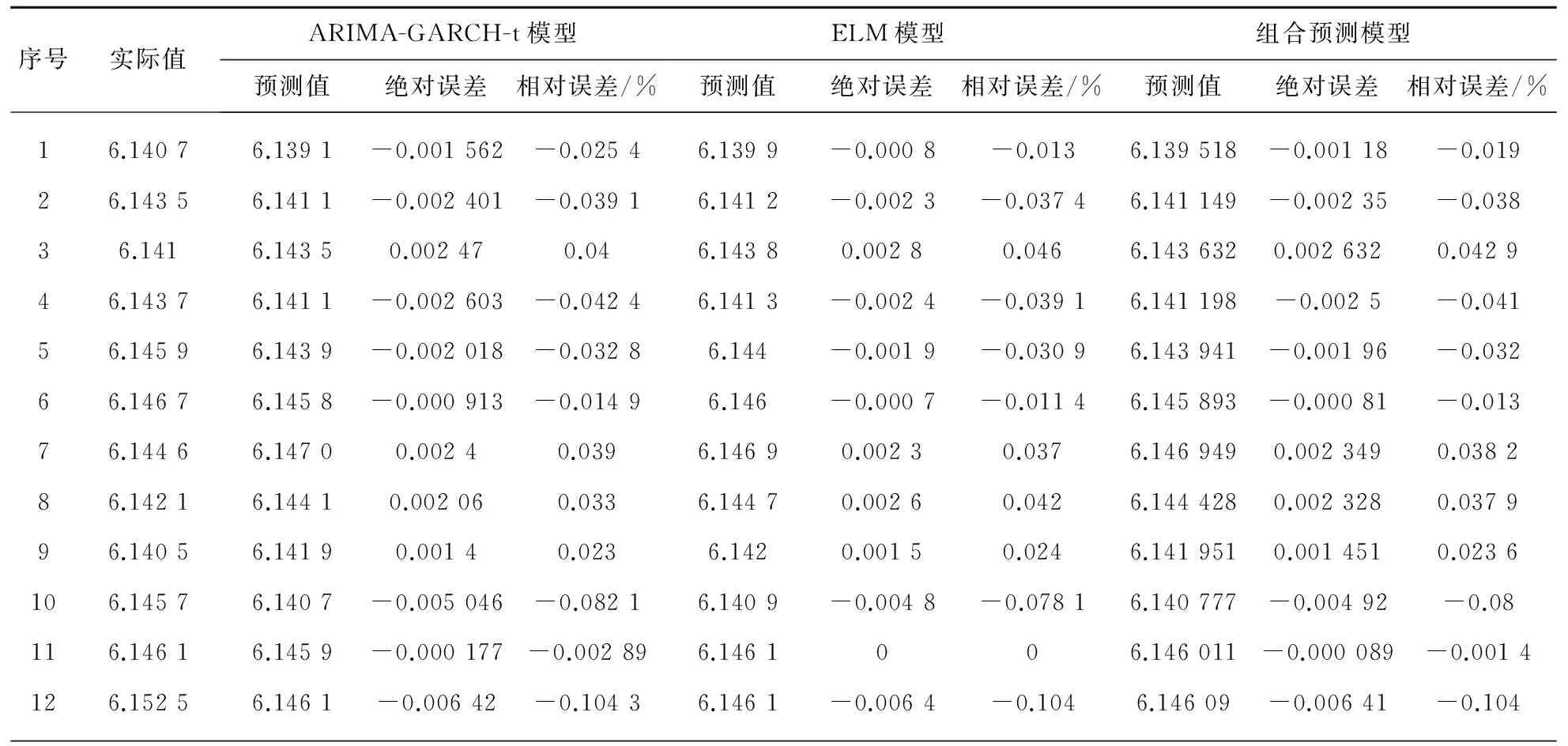
表4 三种模型汇率真实值与预测值比较

表5 三种模型精度对比
3 结论
通常预测模型的误差来源于模型的错误识别,而这种错误识别则是因为预测时仅采取了现有信息的某个子集进行测算时间序列的统计特征.本研究将ARIMA-GARCH-t与ELM组合预测模型运用到汇率的预测中,能充分利用样本预测信息,组合信息使统计推断依据的信息更接近于现有的信息集,在此基础上的推断跟识别更接近真实,从而减少了系统误差,提高了精度.组合预测模型不仅修正了ARIMA模型的异方差性,还考虑随机扰动项对模型的影响,两种非结构预测方法结合还使得预测结果更接近于真实值,可为有关部门提供科学依据.
[1] 谢赤,黄曦,孙柏.基于小波分析与支持向量机的人民币汇率预测[J].湘潭大学学报,2009,(5):82-87.
[2] 殷光伟,付岱山,万志华,等.小波包与神经网络相结合的人民币汇率预测[J].生产力研究,2013 (10):40-42.
[3] Babu C N,Reddy B E.A Moving-average-filter-based hybrid ARIMA-ANN model for forecasting time series data[J].Applied Soft Computing,2014.
[4] 李国勇,闫芳,郭晓峰.基于遗传算法的灰色神经网络优化算法[J].控制工程,2013,20(5):934-937.
[5] 张渊渊,何佳,贾海云.改进的灰色系统理论在汇率预测中的应用[J].计算机仿真,2012,28(11):358-361.
[6] 熊岗,陈章潮.灰色预测模型的缺陷及改进方法[J].系统工程,1992,10(6):32-36.
[7] 汪发余,高振沧,毕建武.基于SPSS组合预测算法的煤炭消费量预测研究[J].资源开发与市场,2014,30(8):957-960.
[8] 李彬,李贻斌.基于ELM学习算法的混沌时间序列预测[J].天津大学学报,2011,44(8):701-704.
[9] 徐勇,王东,张慧.基于自适应在线极限学习机模型的预测方法[J].统计研究,2016,33(7):103-109.
[10] 苏岩,杨振海.GARCH (1,1) 模型及其在汇率条件波动预测中的应用[J].数理统计与管理,2007,26(4):15-620.
[11] 缪灵均,孙欣.基于ARIMA与分段SARMA模型健康保费收入时间序列分析[J].湖州师范学院学报.2015(10):13-18.
[12] 李哲,马中东.组合预测模型在汇率预测中的应用[J].聊城大学学报:自然科学版,2016,29(3):62-66.
[13] Wang Y,Cao F,Yuan Y.A study on effectiveness of extreme learning machine[J].Neurocomputing,2011,74(16):2 483-2 490.
[14] 韩春蕾,高婉君.我国月度CPI的组合预测及分析[J].统计与决策,2014 (1):11-13.
[15] 王瑞庆,王宏福.基于t分布GARCH模型的电价波动时变性研究[J].电力系统保护与控制,2011,39(23):49-53.
Exchange Rate Combined Prediction Model Based on ARIMA-GARCH-t and ELM Model
JI Zhe
(School of Business,Liaocheng University,Liaocheng 252059,China)
This paper aims at predicting the exchange rate to enrich the method of RMB exchange rate prediction. This paper analyses the nonlinear time series characteristics of the RMB exchange rate based on the principle of minimum variance with the data of the central parity data of USD/CNY exchange rate from January 4, 2012 to November 3, 2014 by building combination prediction model of ARIMA-GARCH and ELM. This model, on the one hand, remedies of limitations of heteroskedasticity of residual on the ARIMA prediction accuracy as well as takes the effect of random disturbance term on model into consideration, on the other hand, ELM brings fast-learning and generalization performance superiority into full play. The empirical analysis indicates that the combined prediction model is more effective and accurate than a single forecast method.
exchange rate,ARIMA-GARCH model,ELM,combined predict model
2016-05-12
山东省社科规划项目基金(16DJJJ08)资助
姬喆,E-mail:lcujizhe@163.com.
F012
A
1672-6634(2017)01-0072-06

