广义(2+1)维浅水波方程的精确解①

杨 飞

(聊城大学数学科学学院,山东聊城252059)

广义(2+1)维浅水波方程的精确解①

杨 飞

(聊城大学数学科学学院,山东聊城252059)

通过行波解法将广义(2+1)维浅水波方程转化为常微分方程,然后借助辅助方程得到大量新的精确解,其中包括椭圆函数解、双曲函数解、三角函数解等.

行波解法,辅助方程,精确解

0 引言

浅水波方程是一类重要的非线性偏微分方程,广泛应用于描述环境科学、流体动力学领域中的非线性现象,给人类造成重大灾难的海啸即是一种浅水波.因此构建此类非线性演化方程的精确解有其重要的科学意义和广泛的应用背景.

考虑(2+1)维广义浅水波方程

uxxxy-3uxxuy-3uxyux+auxx+buxy+cuyt=0,

(1)

文献[1]中作者利用奇异流形方法构造了(2+1)维广义浅水波方程的Lax对和相关的Darbuox变换,通过使用得到的Darbuox变换,得到了该方程的一次和二次迭代解以及一个包含任意函数的N孤子解.文献[2]中作者在Riccati方程方法的基础上提出了新的广义投射Riccati方程展开法及其算法.利用这个方法研究了(2+1)维浅水波方程,并得到了许多新的精确解,其中包括类孤子解和类周期解.在文献[3]中作者通过扩展的齐次平衡法研究了(2+1)维广义浅水波方程,得出了方程的Backlund变换、色散关系以及新的孤波解.

1 Jacobi椭圆函数作辅助方程求解

下面考虑方程(1)的行波解,包括有理函数解、双曲函数解、三角函数解等.

令u=u(ξ),ξ=x+λy+μt,代入方程(1)得

λu(4)-6λu″u′+(a+bλ+cλμ)u″=0,

(2)

将方程(2)积分一次得

λu(3)-3λu′2+(a+bλ+cλμ)u′=A,

(3)

再令

v=u′,

(4)

方程(3)化为

λv″-3λv2+(a+bλ+cλμ)v=A

(5)

假设v的表达式

考虑方程中最高阶导数项v″与最高次项v2齐次平衡,由2m+2=3m,可确定平衡数m=2,因而可设方程(5)的解有

v=p2φ2+p1φ+p0,p2≠0,

(6)

(φ′)2=r+αφ2+βφ4,

(7)

将(6)式和(7)式代入方程(5),令φ的同次幂系数为零得到一个代数方程组

解以上代数方程组得

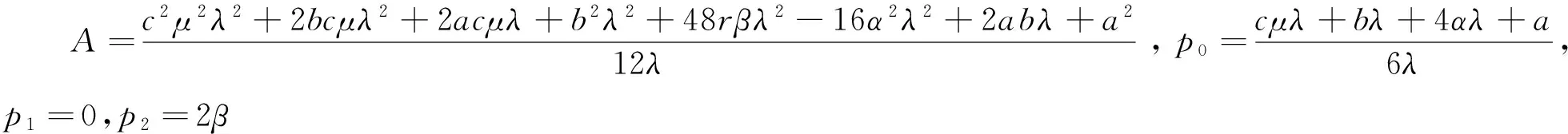
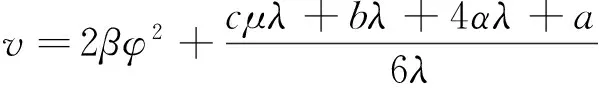
(8)

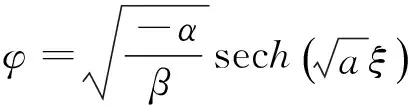
为了能够更加清晰地表述所求方程的解,对解的表达式中的常数选取特定的值,我们可以令a=1,b=1,c=2,μ=1,λ=5,α=2.然后在不同的时间点上,我们能够观察到函数的变化.图1和图2,图3和图4分别是同一情况下不同时间点的函数图像.

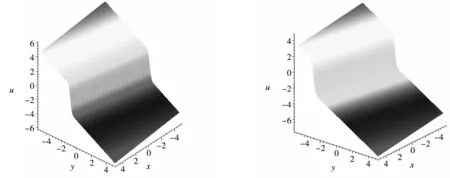
图1 情况1(1)中t为0.01的函数图像 图2 情况1(1)中t为10的函数图像

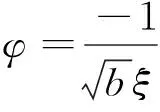
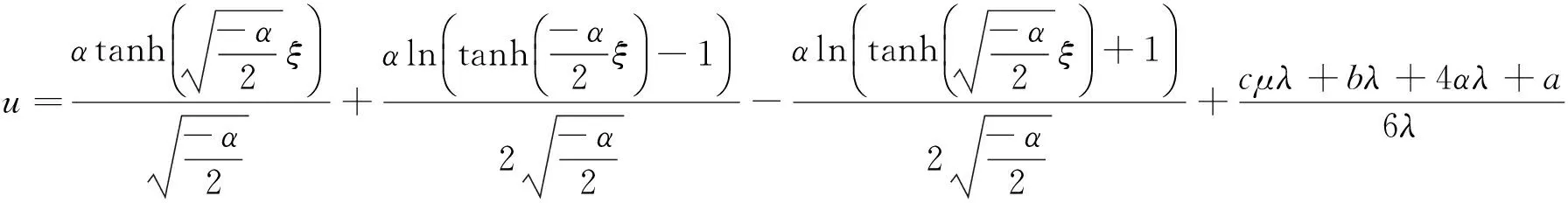
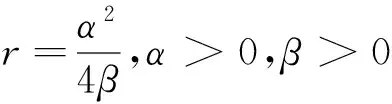
图3 情况2(2)中t为0.01的函数图像 图4 情况2(2)中t为10的函数图像

2 Riccati方程作辅助方程求解

u=k0+k1G,k1≠0,

(9)

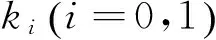
G′=r+αG+βG2.

(10)

将(9)式和(10)式代入方程(3),令G的同次幂系数为零得到一个代数方程组

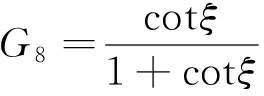
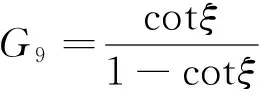
3 结论

本文利用行波解法得到了广义(2+1)维浅水波方程大量的精确解,这些精确解在数学物理中有着重要的作用,值得进一步研究.

[1]ChengC,LiuXL.Backlundtransformandnewexactsolutionsof(2+1)dimensionalgeneralizedshallowwaterwaveequation[J] .JournalofSichuan,2015,38(3):326-328.

[2]MeiJQ,ZhangHQ.Soliton-likeandperiodic-likesolutionsof(2+1)dimensionalgeneralizedshallowwaterwaveequation[J].JournalofDalianUniversityofTechnology,2005,45(4):612-616.

[3]FuHM,DaiZD.Periodicwavesolutionsof(2+1)dimensionalgeneralizedofshallowwaterwaveequation[J].JournalofQiqiharUniversity,2013,29(6):75-77.

[4] 陈立,屈改珠,何姝琦.(3+1)维波动方程的不变集和精确解[J].西北大学学报:自然科学版,2016,46(2):172-177.

[5] 刘式适,刘式达.物理学中的非线性方程[M].北京大学出版社,2000.

[6] 李宁.两类非线性发展方程的精确解[J].聊城大学学报：自然科学版,2012,25(2):1-5.

[7] 陈美.耦合的Ramani方程组的对称约化和精确解[J].聊城大学学报:自然科学版,2011,24(3):1-4.

[8] 辛祥鹏,张琳琳.一种构造Byrgers和KP方程孤立子解和周期解的方法[J].聊城大学学报:自然科学版,2009,22(4):16-20.

[9]ZhaoXQ,ZhiHY,ZhangHQ.ImprovedJacobi-functionmethodwithsymboliccomputationtoconstructnewdouble-periodicsolutionsfortheGeneralizedItosystem[J].Chaos,solutionsandFractals, 2006,28:112-116.

[10]WangDS,LiHB.Ellipticequation’snewsolutionsandtheirapplicationstotwononlinearpartialdifferentialequations[J].ApplMathComput,2007,188:762-771.

[11] 李康,刘洪吉.广义MKP方程的对称约化和精确解[J].聊城大学学报:自然科学版,2015,28(1):19-23.

[12] 闫志莲.Zacharov-Kuznetsov方程的显式解[J].聊城大学学报:自然科学版,2004,17(1):14-15.

[13] 张颖元,王岗伟,刘希强.(2+1)维非线性发展方程的对称约化和显式解[J].量子电子学报,2012,29(4):411-416.

[14]YombaE.OnexactsolutionsofthecoupledKlein-Gordon-SchrodingerandthecomplexcoupledKdVequationsusingmappingmethod[J].Chaos,solutionsandFractals,2004,2:206-229.

[15] 张琳琳,辛祥鹏.(2+1)维修正的KP方程的精确解[J].聊城大学学报:自然科学版,2009,22(3):9-13.

Exact Solutions for a Class of Generalized (2+1)- Dimensional Shallow Water Equation

YANG Fei

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059, China)

By applying traveling wave method , generalized (2+1)-dimensional shallow water equations is converted into ordinary differential equations,and then with the aid of auxiliary equation to get a large number of new exact solutions,which included elliptical function solution, hyperbolic function solutions, triangle function solutions and so on.

traveling wave method,auxiliary equation ,exact solution

2016-10-20

国家自然科学基金与中国工程物理研究院基金项目(11076015)资助

杨飞，E-mail:2462407828@qq.com.

O175

A

1672-6634(2017)01-0022-05