(3+1)维Zakharov-Kuznetsov-Burgers方程的精确解和守恒律①

李 玉 李立群 李会会 刘希强

(1.聊城大学数学科学学院，山东聊城252059;2.山东农业工程学院，山东济南250100)

(3+1)维Zakharov-Kuznetsov-Burgers方程的精确解和守恒律①

李 玉1李立群2李会会1刘希强1

(1.聊城大学数学科学学院，山东聊城252059;2.山东农业工程学院，山东济南250100)

利用待定系数法得到了(3+1)维Zakharov-Kuznetsov-Burgers方程的对称、单参数群和约化方程. 结合幂级数展开法和tanh函数展开法以及Riccati辅助函数的应用, 我们得到了该方程的一些新精确解, 包括行波解、有理函数解、周期解、三角函数解等.最后,基于所求对称和该方程伴随方程的解, 得到了方程的守恒律.

Zakharov-Kuznetsov-Burgers方程,对称约化,精确解,守恒律

1 研究背景

随着科学技术的迅速发展和人们对自然现象的不断深入了解, 对于非线性发展方程精确解的研究一直都是物理、化学、数学等众多领域关注的重要课题. 因此越来越多的数学家和物理学家致力于精确解的研究,并且提出了许多著名有效的方法, 包括指数函数展开法[1],F-函数展开法[2],Bäcklund变换法[3,4],经典李群方法[5,6]和非经典李群方法,Jacobi椭圆函数展开法[7,8], 齐次平衡法[9,10]以及tanh函数展开法[11,12]等. 利用这些方法得到许多丰富的精确解, 包括孤子解、三角函数解、紧致类解等. 尤其是经典李群方法, 可以系统地研究方程的群变换解及守恒律，是研究精确解的有力工具之一.

(3+1)维Zakharov-Kuznetsov-Burgers方程形式

ut+auux+buxxx+c(uxyy+uxzz)+duxx=0，

(1)

其中a,b,c和d是任意常数.

取d=0, 方程(1)变为(3+1)维Zakharov-Kuznetsov方程

ut+auux+buxxx+c(uxyy+uxzz)=0.

20世纪80年代末,Zakharov和Kuznetsov在描述磁化等离子体德尔演化过程中首次导出该模型. 也就是说Zakharov-Kuznetsov方程是最早描述非线性离子声波的模型, 同时它也是描述二维KdV方程的最好模型之一, 在物理学的许多领域中不断出现, 并且取得了很多研究成果.

取a=6,b=1,c=3,d=0, 结合Wronskian形式展开法, 求得了双孤子解、双三角函数解、Complexiton解、Matveev解和Jacobi椭圆函数解[15].

取c=0, 方程(1)变为KdV-Burgers方程

ut+auux+buxxx+duxx=0.

(2)

KdV-Burgers方程目前已取得了大量研究成果. 文献[16]在引入典型无扰动任意次广义KdV-Burgers方程扭状孤立波解的基础上, 研究了扰动方程的具有任意精度的近似解; 文献[17] 讨论了一类具有阻尼和非齐次项的KdV-Burgers方程的概周期解存在性问题.

本文的结构: 第2部分, 利用待定系数法求得方程(1)的李点对称; 第3部分, 通过求解特征方程组, 结合tanh函数展开法和幂级数展开法以及Riccati辅助方程, 得到方程(1)的约化方程和精确解；第4部分, 通过对称和约化方程, 给出了方程的守恒律. 第5部分, 得出相关结论.

2 Zakharov-Kuznetsov-Burgers方程的对称

对于非线性发展方程

F(x,y,t,u,ux,uy,ut,uxx,uxt,…)=0,

(3)

称函数σ(x,y,t,u,ux,uy,ut,uxx,…)为方程(1)的对称, 如果

F′(u)σ=0,

(4)

对于任意的u都成立, 其中

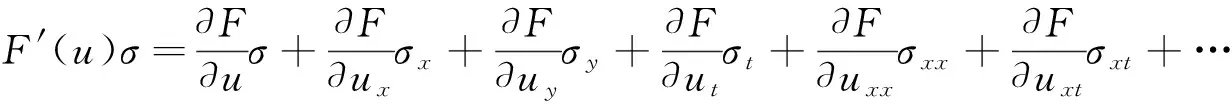
利用方程(4), 可以得到方程(1)的李点对称σ满足

σt+auσt+aσut+bσxxx+c(σxyy+σxzz)+dσxx=0.

(5)

下面利用待定系数法求方程(1)的李点对称σ, 设方程(5)的解为

σ=a1ut+b1ux+c1uy+d1uz+e1u+g1,

(6)

a1=c5,b1=-ac1t+c2,c1=c3z+c4,d1=-c3y+c6,e1=0,g1=c1,

(7)

其中c1,c2,c3,c4,c5和c6为任意常数. 因此, 可以得到方程(1)的李点对称

σ=c5ut+(-ac1t+c2)ux+(c3z+c4)uy+(-c3y+c6)uz+c1,

(8)

由以上对称, 可以得到生成元为

(9)

为了得到方程(1)的李点对称群, 需要考虑以下初值问题

(10)

其中ε是无穷小参数. 解方程(10), 可以得到单参数群gi(i=1,2,3,4,5,6)如:

g1=(t,-ac1tε+x,y,z,-c1ε+u),g2=(t,c2ε+x,y,z,u),

g3=(t,x,zsin(c3ε)+ycos(c3ε),-ysin(c3ε)+zcos(c3ε),u),

g4=(t,x,c4ε+y,z,u),g5=(c5ε+t,x,y,z,u),

g6=(t,x,y,c6ε+z,u),

其中g2,g4,g5和g6表示方程(1)解的时空不变性,g3表示方程(1)解在移动坐标系中的伽利略变换不变性.

由单参数群gi(i=1,2…5,6)可以得到方程(14)的解的表达式

u1=-c1ε+f(t,-ac1tε+x,y,z),u2=f(t,c2ε+x,y,z),

u3=f(t,x,zsin(c3ε)+ycos(c3ε),-ysin(c3ε)+zcos(c3ε)),u4=f(t,x,c4ε+y,z),

u5=f(c5ε+t,x,y,z),u6=f(t,x,y,c6ε+z).

其中ε是参数,f是方程(2)的任意已知解.

3 Zakharov-Kuznetsov-Burgers方程的相似约化和精确解

为了求出方程(1)的相似约化和精确解, 必须解相应的特征方程组, 方程(1)对应的对称的特征方程组为

选取下述情况进行讨论.

情况1 当c1=0,c2=0,c3=0,c4≠0,c5≠0,c6≠0时, 解相应的特征方程组可得

u=f(ξ,η,γ),η=c4t-c5y,ξ=x,γ=c4z-c6y,

将其代入方程(1)得约化方程

(11)

下面利用tanh函数展开方法求解方程. 作行波变换f(ξ,η,γ)=f(ω),ω=lξ+kη+λγ, 代入(11)式得到

(12)

其中l,k和λ是任意非零常数.利用齐次平衡法, 可得n=2, 设上式有以下形式的解

(13)

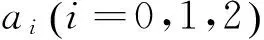
Y=tanh(μω),

(14)

将(13)式代入(12)式, 并利用(14)式, 令Y的同次幂项的系数为零, 可得到下面4组结果

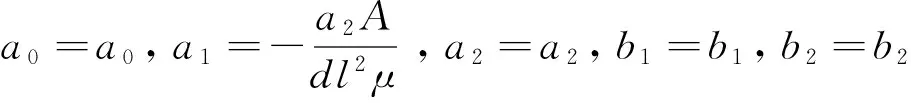
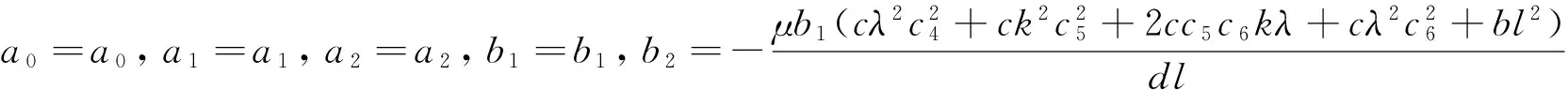
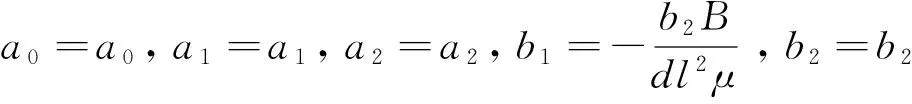
由此, 我们可得到方程(1)的解, 如

情况2 当c1=c3=c5=c6=0,c2=c4=1时, 解相应的特征方程组可得u=f(ξ,η,γ),η=x-y,ξ=t,γ=z,将其代入方程(1)得约化方程

fξ+affη+(b+c)fηηη+cfηγγ+dfξξ=0,

(15)

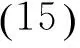
lf′+akff′+dk2f″+((b+c)k3+ckλ2)f‴=0,

(16)

其中l,k和λ是任意非零常数.

以下利用幂级数展开法求解方程(16)的解, 假设方程(16)有下述形式的解

(17)

由方程(17), 可以得到

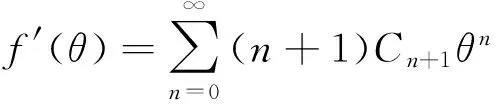
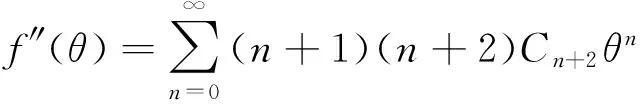
(18)

把方程(17)和方程(18)代入到方程(16), 得到

(19)

当n=0时, 我们可以得到

(20)

一般地, 当n≥1时, 由方程(19), 可以求得

(21)

事实上, 方程(16)的解为

(22)

因此,方程(1)的精确幂级数解为

u5=C0+C1(lt+k(x-y)+λz)+C2(lt+k(x-y)+λz)2

其中Ci(i=0,1,2,3)为任意常数.

情况3 当c1=c2=c5=0,c3≠0,c4≠0,c6≠0时, 解相应的特征方程组可得

将其代入方程(1)得约化方程

利用Riccati辅助方程求解上述约化方程. 做行波变换f(ξ,η,γ)=f(ζ),ζ=lξ+kη+λγ, 代入上式得到以下变系数方程

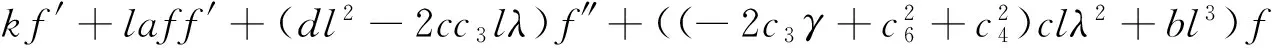
(24)

通过平衡(24)式中的最高阶导数项和非线性项, 可得(24)式应有满足下式的解

f=q0(λ)+q1(γ)ψ(ζ)+q2(γ)ψ(ζ)2,

(25)

其中ψ=ψ(ζ)满足Riccati方程

ψ'=h0+h1ψ+h2ψ2,

(26)

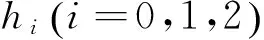
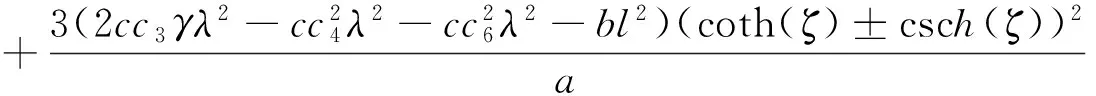
2)当h0=1,h1=0,h2=1时,ψ3=tan(ζ), 则原方程的解为

3)当h0=-1,h1=0,h2=-1时,ψ4=cot(ζ), 则原方程的解为

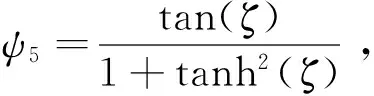
4 Zakharov-Kuznetsov-Burgers方程的守恒律

守恒律被广泛地应用于非线性数学物理科学中. 特别是对于非线性物理量的稳定性和存在唯一性的分析起着非常重要的作用. 以下利用方程(1)的伴随方程和对称(8)来研究方程(1)的守恒律. 经计算, 得到方程(1)的共轭方程为

vt+auvx+bvxxx+c(vxyy+vxzz)+dvxx=0,

(27)

最高阶拉氏量为

L=v(ut+auux+buxxx+c(uxyy+uxzz)+duxx).

(28)

定理1 每个李点对称、李贝克隆变换和方程(1)的对称(8)都给出了(3+1)维Zakharov-Kuznetsov-Burgers方程及其共轭方程的一个守恒律, 且守恒向量(Cx,Cy,Ct,Cz)由下式给出

(29)

由对称(8), 取W=-1+atux, 可得C1=(-1+atux)v,C2=-atv(ut+auux+buxxx+c(uxyy+uxzz)+duxx)+(atux-1)(auv-dvx+bvxx+cvyy+cvzz)+atuxx(dv-bvx)+abtvuxxx,C3=(-1+atux)cvxy,C4=(-1+atux)cvxz.守恒向量(Cx,Cy,Ct,Cz)包含共轭方程(27)的任意解v, 因此上式给出了方程(1)的无穷多个守恒律.

5 结论

本文利用待定系数法求出了(3+1)维Zakharov-Kuznetsov-Burgers方程的对称和单参数群, 并且得到了该方程的相似约化方程, 再借助于tanh函数展开法和幂级数展开法以及Riccati辅助方程, 求出了原方程的一些新精确解, 有行波解、有理函数解、周期解、三角函数解等. 最后, 通过对称和共轭方程给出了该方程的守恒律. 这些精确解在很多工程技术、物理、化学等领域起着不可或缺的作用, 同时也表明了李群方法是求解非线性发展方程一种非常有用的方法, 值得我们做进一步的努力进行研究.

[1]ZhengB.Exp-functionmethodforsolvingfractionalpartialdifferentialequations[J].TheScientificWorldJournal, 2013, 2013:465723.

[2]AbdouMA.TheextendedF-expansionmethodanditsapplicationforaclassofnonlinearevolutionequation[J].Chaos,SolitonFract, 2007,31:95-104.

[3]HeJH,WuXH.Exp-functionmethodfornonlinearwaveequation[J].ChaosSolitonsandFractals, 2006, 30(3): 700-708.

[4]M.Wadati.WavepropagationinnonlinearlatticeII[J].JournalofthePhysicalSocietyofJapan, 1975, 38(3): 681-686.

[5] 陈美,刘希强,王猛. 对称正则长波方程组的对称,精确解和守恒律[J].量子电子学报,2012,29(1):21-26.

[6] (2+1)维非线性发展方程的对称约化和显式解[J].量子电子学报,2012,29(4):411-416.

[7] 刘勇,刘希强,王振立. (2+1)维PotentialBoiti-Leon-Manna-Pempinelli方程的对称、约化和精确解[J].量子电子学报, 2014, 31(5): 433-440.

[8] 李宁,刘希强.推广的Pochhammer-Chree方程的显式解[J]. 聊城大学学报：自然科学版,2013,26(1): 1-4.

[9]FanEG,ZhangH.Anoteonthehomogeneousbalancemethod[J].PhysLettA, 1998, 246(5): 403-406.

[10]FanEG,HongYC.Generalizedtanhmethodextendedtospecialtypesofnonlinearequations[J].ZeitschriftfurNaturforschungA-JournalofPhysicalSciences, 2002, 57(8): 692-700.

[11] 王振立,刘勇.一类非线性发展方程的精确解[J]. 聊城大学学报：自然科学版, 2013,26(2): 16-19.

[12]Abdel-AllNH,Abdel-RazekMAA,SeddeekAAK.Expandingthetanh-functionmethodforsolvingnonlinearequations[J].AppliedMathematics, 2011, 2(9): 1 096-1 104.

[13]MoslemWM,SabryR.Zakharow-Kuznetsov-Burgersequationfordustionacousticwaves[J].Chaos,SolitonsandFractals, 2008, 36(3):628-634.

[14]WazwazAM.NonlineardispersivespecialtypeoftheZakharov-KuznetsovequationZK(n，n)withcompactandnoncompactstructures[J]．ApplMathComput，2005，161：577-590．

[15] 崔艳英,吕大昭,刘长河.(3+1)维Zakharov-Kuznetsov方程的Wronskian形式解[J].北京建筑工程学院学报,2012, 28(2): 68-71.

[16] 洪宝剑,卢殿臣.一类广义扰动KdV-Burgers方程的同伦近似解[J].物理学报, 2013,62(17): 24-28.

[17] 施秀莲.一类KdV-Burgers方程的概周期解[J].工程数学学报, 2014, 31(1): 67-74.

Exact Solutions and Conservation Laws of the (3+1) Dimensional Zakharov-Kuznetsov-Burgers Equation

LI Yu1LI Li-qun2LI Hui-hui1LIU Xi-qiang1

(1.School of Mathematical Sciences, Liaocheng University, Liaocheng 252059, China;2.Shandong Agriculture and Engineering University, Jinan 250100,China)

By applying undetermined coefficient method, the classical Lie symmetry and reduced equation of the (3+1) dimensional Zakharov-Kuznetsov-Burgers equation were obtained. At the same time, a great many of solutions are derived by solving the reduction equations with power series expansion method and the tanh function expansion method and Riccati auxiliary equation, including travelling wave solutions, the rational function solutions, hyperbolic function solutions, the trigonometric function solutions and so on. Finally, the conservation laws of the equation are obtained by using the symmetry and adjoint equations.

Zakharov-Kuznetsov-Burgers equation，symmetry reduction，exact solutions, conservation laws

2016-11-20

国家自然科学基金和中国工程物理研究院联合基金项目(11076015)资助

刘希强，E-mail:liuxiq@sina.com.

O175.2

A

1672-6634(2017)01-0010-08