纤维螺旋缠绕管的缠绕角优化

耿 沛， 邢静忠， 陈晓霞

(1. 北京航空航天大学 航空科学与工程学院， 北京 100191； 2. 天津工业大学 机械工程学院， 天津 300387； 3. 天津市现代机电装备技术重点实验室, 天津 300387)

纤维螺旋缠绕管的缠绕角优化

耿 沛1，2， 邢静忠2,3， 陈晓霞2

(1. 北京航空航天大学 航空科学与工程学院， 北京 100191； 2. 天津工业大学 机械工程学院， 天津 300387； 3. 天津市现代机电装备技术重点实验室, 天津 300387)

为提高材料强度的利用效率,实现纤维缠绕管强度比沿壁厚的均匀分布，在内压和轴向力作用下，基于Tsai-Wu准则，以沿壁厚方向的最小强度比最大化为目标，建立变缠绕角纤维缠绕管的最优化模型。提出将复合形法和梯度法相结合的改进优化算法，通过优化逐层变化的缠绕角使最小强度比最大化，实现强度比沿壁厚更均匀分布。以玻璃纤维管为例，在纯环向应力、环向应力与轴向应力之比为2∶1和1∶1的3种工况下，研究不同壁厚条件下最优缠绕角分布及其强度比提升效果和均匀程度。结果表明：优化后结构的材料利用率明显提升，不同工况、壁厚对最优缠绕角的分布规律影响很大；最优缠绕角可以实现沿壁厚等强度。

纤维缠绕管； 缠绕角； 失效准则； 纤维向应力

高性能的纤维缠绕压力容器和管道在诸多领域得到广泛应用[1-2]。文献[3-6]通过施加内压和轴向力，研究变缠绕角纤维缠绕结构在不同的应力比下抵抗破坏的能力。结果表明，与单一缠绕角结构相比，变缠绕角结构表现出更优异的抵抗破坏能力。理论分析和实验研究[7-9]表明，单一缠绕角的纤维缠绕薄壁管道在施加内压或经受环向应力与轴向应力之比为2∶1的荷载下，最优缠绕角在55°左右。文献[10]比较研究了薄壁筒理论和厚壁筒理论对应的强度随壁厚和缠绕角的分布规律，发现55°缠绕角容器的内外侧强度比差别很大。变化缠绕角有可能提高材料利用率，提高结构的承载能力。三维分析发现铺层顺序对结构承压性能有很大影响[11-13]。文献[14]利用正交各向异性本构关系和轴对称理论，在内外压及轴向力作用下，给出变缠绕角缠绕厚壁筒任意缠绕层的应力和变形。

基于三维正交弹性理论的结构分析提出过许多缠绕结构的优化方法，如何通过变化缠绕角以提高纤维缠绕结构的材料利用率还有待研究。1988年，Tsai首次对变缠绕角纤维缠绕厚壁柱形容器缠绕角的优化进行研究[1]。但是直到2006年，Tabakov才利用Tsai-Wu失效准则和遗传算法，通过变化缠绕角对纤维缠绕厚壁柱形容器进行缠绕角优化分析[15]。这些研究只是提高了最小强度比，并没有找到实现沿壁厚等强度的最优缠绕角分布。

本文按照文献[14]变缠绕角纤维缠绕厚壁管道在内压和轴向力作用下的应力变形和纤维向应力，基于Tsai-Wu失效准则，建立多种应力状态下变缠绕角纤维缠绕管的缠绕角最优化模型。比较分析传统复合形法和梯度法的计算效率和结果差异，提出将2种传统优化算法相结合的改进优化算法。以壁厚方向的最小强度比最大化和实现强度比更均匀分布为目标，寻找最优缠绕角变化规律。以玻璃纤维管道模型为例，在纯环向应力、环向应力与轴向应力之比为2∶1和1∶1这3种工况下，研究不同壁厚条件下最优缠绕角分布及其强度比提升效果和均匀程度。

1 纤维层应力

采用对称均衡缠绕工艺缠绕形成外半径为rn，内半径为r0的厚壁管道。每2个均衡对称层看成1个正交各向异性层，n个外径为ri(i=1, 2, …,n)的缠绕层，构成变缠绕角纤维缠绕管。

多层具有正交各向异性材料构成的厚壁管道，在内压qa和外压qb以及沿z轴方向轴向力Tz的作用下产生半径r方向和轴线z方向的变形(见图1)。

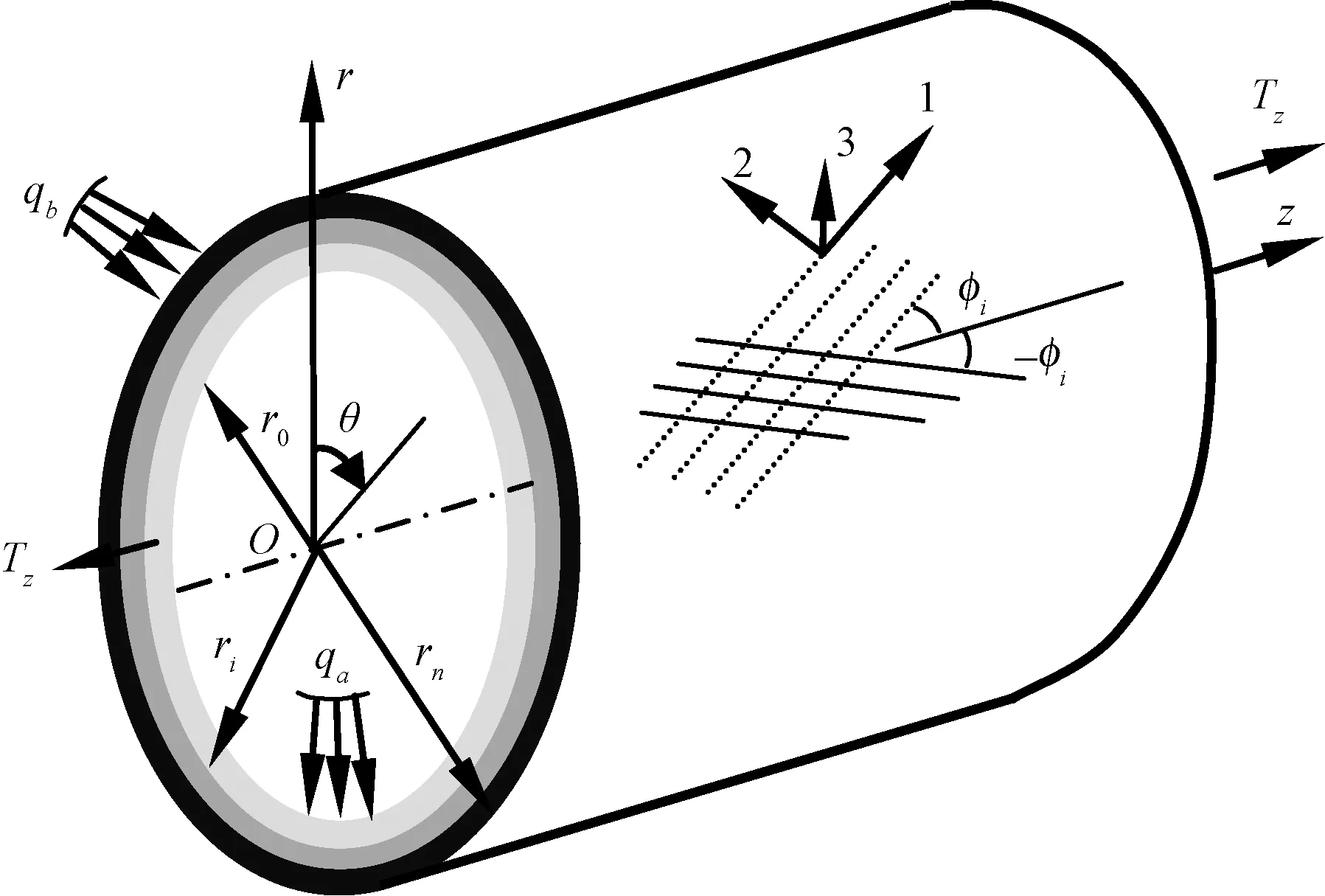
图1 轴对称纤维缠绕厚壁柱形容器力学模型Fig.1 Axisymmetric hybrid filament wound cylinder

1.1 偏轴应力应变关系

由文献[14]可得偏轴刚度系数与正轴刚度系数之间的关系，得到偏轴坐标系下纤维层的应力-应变关系：

(1)

1.2 平衡方程和应力分量

根据文献[16]可得纤维层的位移场：

(2)

其中

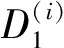
(3)

其中

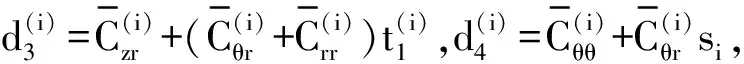
当si=1时，rq方向各向同性，式(2)化为

(4)

其中

(5)

式(4)变为

(6)

其中

1.3 边界条件

由内外壁边界条件、层间位移连续应力连续条件及z向平衡方程[16]，可以确定积分常数和轴向应变的方程组[14]：

[K]{δ}={qi}

(7)

[K]为刚度矩阵[14]，求解式(7)，可得每层的位移、应变和应力。

1.4 三维纤维向应力公式

由文献[14]可得纤维向应力公式，见式(8)。当si=1时，纤维向应力公式变为式(9)。

(8)

(9)

2 优化模型和优化方法

获得纤维向应力后，可基于失效准则判定危险点的安全度。这里选用三维Tsai-Wu准则计算危险点的强度比。

2.1 强度比计算

基于三维Tsai-Wu 准则[10]定义强度比，如式(10)所示。

(10)

式中：

ξ=Fr(σ2+σ3)+Fzσ1。

2.2 工况和缠绕角初值计算

取玻璃纤维/树脂基作为缠绕材料，材料参数[17]为E1=43.4 GPa,E2=15.2 GPa,G12=6.14 GPa,n21=0.29,n32=0.38,Xt=1 062 MPa,Xc=610 MPa,Yt=31 MPa,Yc=118 MPa,S=72 MPa。在管内壁施加内压qa=0.111 111 MPa，管道端部施加内压引起轴向力πr02qa。它们在管壁分别形成环向应力与轴向应力比2∶1，1∶1和纯环向应力的3种工况。

取缠绕层数n=1、3、5、10、15、20，在内外半径比r0/rn为0.95、0.90、0.85、0.80、0.75、0.70、0.65的条件下，优化计算纤维缠绕管道的缠绕角，以及各组最优缠绕角对应的强度比分布规律。对于单一缠绕角的薄壁管，最优缠绕角为55°[5-9]，取f=55°作为初始缠绕角。

2.3 复合形-梯度法的提出

分别使用复合形法和梯度法对缠绕角进行优化计算。研究发现：对于不同内外半径比和不同缠绕层数的缠绕管道，复合形法得到的最优缠绕角波动非常大，分布不平滑，对应的强度比分布上下波动，不够均匀；梯度法给出的缠绕角变化比较平滑，但最小强度比并没有达到复合形法的结果，未能实现最小强度最大化。

为此，本文提出一个新的优化算法：复合形-梯度法。其优化过程如下：首先使用复合形法得到各缠绕层的缠绕角，然后将其进行函数拟合，得到缠绕角的分布函数，再使用梯度法继续对其优化。

优化计算结果显示：对于不同壁厚和不同缠绕层数的模型，当层数n达到20层后缠绕角趋于稳定，其强度比变化非常平坦。

3 优化结果分析

对不同内外半径比的玻璃纤维管，使用复合形-梯度法对前述3种工况分别进行计算。图2～4分别示出n为300时，内外半径比r0/rn为0.95、0.80和0.65这3种情况下，初始缠绕角和最优缠绕角及其相应的强度比沿着壁厚的分布。

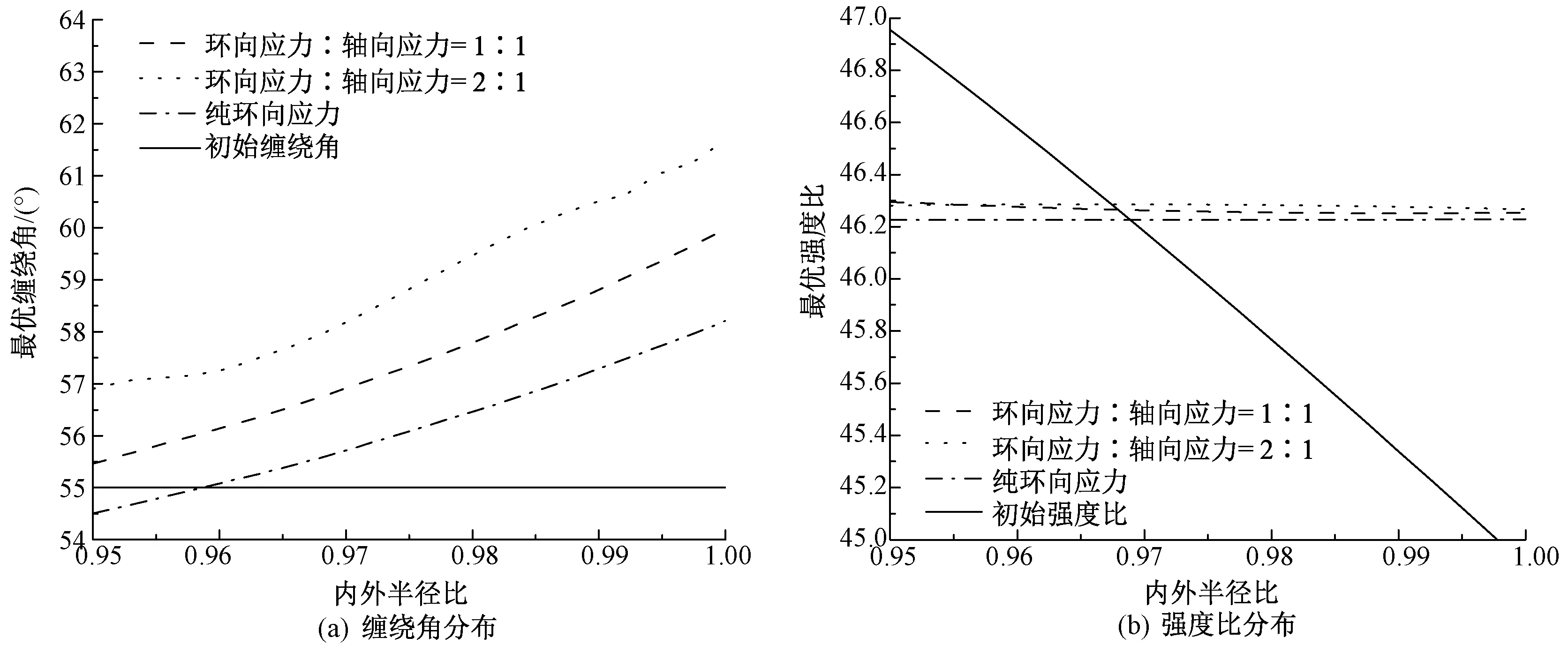
图2 内外半径比为0.95时玻璃纤维管的缠绕角分布与强度比分布Fig.2 Original and aptimized winding angles and strength radtio distributions of Eglass/epoxy pipe at r0/rn=0.95

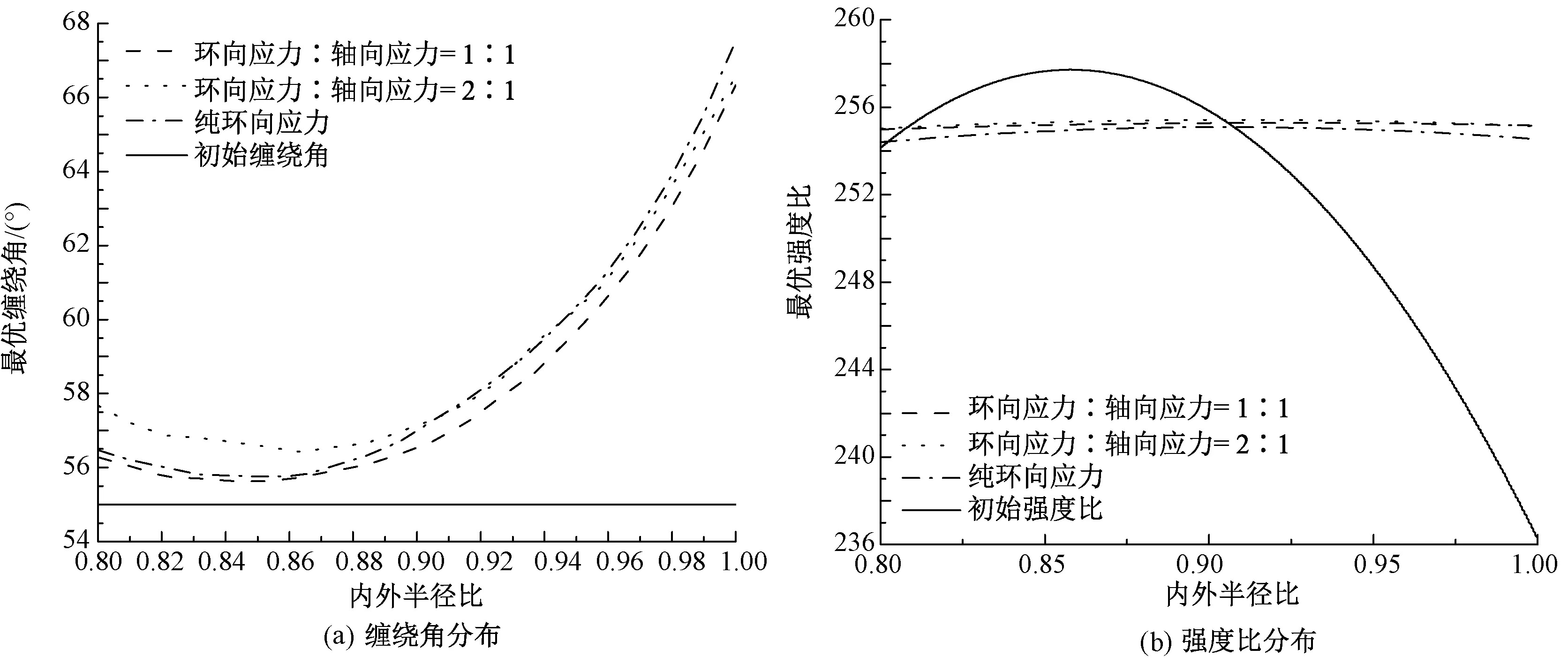
图3 内外半径比为0.80时玻璃纤维管的缠绕角分布与强度比分布Fig.3 Original and aptimized winding angles and strength radtio distributions of Eglass/epoxy pipe at r0/rn=0.80

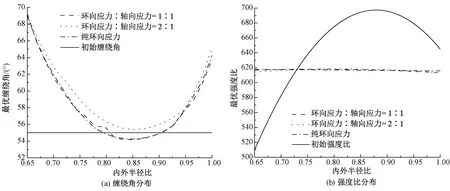
图4 不同内外半径比下玻璃纤维管的缠绕角及强度比沿壁厚的分布Fig.4 Original and optimized winding angles and strength ratio distributions of E-glass/epoxy pipe at ro/rn=0.65

从图2看出，对于较薄(r0/rn=0.95)的玻璃纤维管，最优缠绕角从内向外逐渐增大，优化后的强度比沿壁厚分布均匀。从图3看出，对于中等厚度(r0/rn=0.80)的玻璃纤维管，优化缠绕角呈现内低外高的抛物线分布，其强度比沿壁厚分布均匀；从图4看出，对于很厚(r0/rn=0.65)的玻璃纤维管，优化缠绕角呈现内高外低，中间最低的抛物线分布，其强度比沿壁厚分布均匀。玻璃纤维缠绕角的分布规律表明，当层数n很大时，缠绕角的变化趋于稳定，强度比呈近似直线分布。3种工况下各层的强度比达到最大值并且沿壁厚均匀分布。

表1示出强度比差值率。可看出：初始方案的强度比最大值和最小值的差值率分别为4.37%、8.05%和26.17%；而优化后方案n=20的差值率为0.33%、1.66%和2.49%；n=300的差值率为0.086%、0.160%和0.850%。这表明对于厚壁玻璃纤维管易实现最小强度比最大化及强度比沿壁厚均匀分布。

表1 玻璃纤维管初始缠绕角和最优缠绕角的强度比差值率Tab.1 Comparison of strength ratio of original and optimized winding angles of E-glass/epoxy pipes

4 结 论

1) 不同的优化方法对计算效率和结果的平滑性有很大影响，本文提出的复合形-梯度法明显提升了计算效率，且使最优缠绕角分布更平滑。

2) 不同壁厚的玻璃纤维管的最优缠绕角相差很大；对于很厚的玻璃纤维管，最优缠绕角可提升强度比，并实现强度比沿壁厚的均匀分布。FZXB

[1] TSAI S W. Theory of Composite Design[M]. 4th ed. USA: Think Composites, 1988: 1-5.

[2] SKINNER M L. Trends, advances and innovations in filament winding[J]. Reinforced Plastics, 2006(2): 28-33.

[3] MERTINY P, ELLYIN F, HOTHAN A. An experimental investigation on the effect of multi-angle filament winding on the strength of tubular composite structures[J]. Composites Science and Technology, 2004, 64: 1-9.

[4] SODEN P D, KITCHING R, TSE P C, et al. Influence of winding angle on the strength and deformation of filament-wound composite tubes subjected to uniaxial and biaxial loads[J]. Composites Science and Technology, 1993, 46: 363-378.

[5] SODEN P D, LEADBETTER D, GRIGGS P R, et al. The strength of a filament wound composite under biaxial loading[J]. Composites, 1978(9): 247-250.

[6] SPENCER B, HULL D. Effect of winding angle on the failure of filament wound pipe[J]. Composites, 1978, 9: 263-271.

[7] SODEN P D, KITCHING R, TSE P C. Experimental failure stresses for ±55 filament wound glass fiber reinforced plastic tubes under biaxial loads[J]. Composites, 1989, 20: 125-135.

[8] ELLYIN F, CARROLL M, KUJAWSKI D, et al. The behavior of multidirectional filament wound fibre glass/epoxy tubulars under biaxial loading[J]. Composites, 1997, 28(A): 781-790.

[9] ANTONIOU A E, KENSCHE C, PHILIPPIDIS T P. Mechanical behavior of glass/epoxy tubes under combined static loading: part I: experimental[J]. Composites Science and Technology, 2009, 69(13): 2241-2247.

[10] 邢静忠, 陈利. 内外压作用下纤维缠绕厚壁柱形容器的强度[J]. 复合材料学报, 2011, 28(1): 124-131. XING Jingzhong, CHEN Li. Strength of filament wound thick-walled cylindrical vessel under internal and external pressure[J]. Acta Materiae Compositae Sinica, 2011, 28(1): 124-131.

[11] ROY A K, TSAI S W. Design of thick composite cylinders[J]. Journal of Pressure Vessel Technology, 1988, 110: 255- 262.

[12] COHEN D. Influence of filament winding parameters on composite vessel quality and strength[J]. Composites Part A, 1997, 28: 1035-1047.

[13] MERTINY P, ELLYIN F, HOTHAN A. Stacking sequence effect of multi-angle filament wound tubular composite structures[J]. Journal of Composite Materials, 2004, 38(13): 1095-1113.

[14] XING J Z, GENG P, YANG T. Stress and deformation of hybrid filament-wound thick cylinder vessel under internal and external pressure[J]. Composite Structures, 2015, 131(1): 868- 877.

[15] TABAKOV P Y, SUMMERS E B. Lay-up optimization of multilayered anisotropic cylinders based on a 3-D elasticity solution[J]. Composite Structures, 2006, 84: 374-384.

[16] 邢静忠, 陈利, 孙颖. 纤维缠绕厚壁柱形容器的应力和变形[J]. 固体火箭技术, 2009, 32(6): 680-685. Xing Jingzhong, CHEN Li, SUN Ying. Stress and deformation of filament-wound thick cylinder vessel under internal and external pressure[J]. Journal of Solid Rocket Technology, 2009, 32(6): 680-685.

[17] GOETSCHEL D B, RADFORD D W. Analytical development of through-thickness properties of composite laminates[J]. Journal of Advanced Materials, 1997, 29(7): 37-46.

Winding angle optimization of filament spiral wound pipe

GENG Pei1，2, XING Jingzhong2,3, CHEN Xiaoxia2

(1.SchoolofAeronauticScience&Engineering,BeihangUniversity,Beijing100191,China; 2.SchoolofMechanicalandElectronicEngineering,TianjinPolytechnicUniversity,Tianjin300387,China; 3.TianjinKeyLaboratoryofAdvancedMechatronicsEquipmentTechnology,Tianjin300387,China)

More uniform strength for all layers can be achieved by variation of winding angle to improve the utilization efficiency of filament wound (FW) pipe. An optimization model of FW pipe under uniform internal pressure and axial force is built based on Tsai-Wu failure criterion to maximize the lowest strength ratio along the thickness direction. An improved optimization algorithm derived from two conventional methods (complex method and steepest descent method) is proposed by optimizing the winding angle of the layer by layer, and the minimum strength ratio is maximized. In three cases of pure hoop stress and the ratios of hoop stress to axial stress of 2∶1 and 1∶1, an optimization model of pipes made of E-glass/epoxy is illustrated to evaluate the improvement of the minimum strength ratio and the uniformity of the optimized winding angle distributionunder different ratio of thickness to radius, respectively. The research shows that the material utilization can be increased by proper winding angle variation. A quite uniform distribution of strength ratio along thickness can be realized easily by the optimization of the winding angle.

filament wound pipe; winding angle; failure criterion; fiber stresses

10.13475/j.fzxb.20160105306

2016-01-26

2016-06-15

国家自然科学基金资助项目(51575390); 天津市应用基础与前沿技术研究计划一般项目(14JCYBJC19200)

耿沛(1989—)，男，硕士生。研究方向为复合材料结构力学。邢静忠，通信作者，E-mail：hsingjzh@tjpu.edu.cn。

TB 332； O 343

A