三角函数中一类“会而易错”的问题
江苏省梅村高级中学(214112) 马红燕●
三角函数中一类“会而易错”的问题
江苏省梅村高级中学(214112)
马红燕●
从当今江苏高中数学内容与要求来看,三角函数一块内容相对于函数与数列来讲较为简单,学生也较易理解.但从实际情况来看,三角函数中的一类问题:有关考查到三角函数中sinα+cosα、sinα-cosα、sinαcosα这三者关系的运用时,学生往往“会而失分”.本文将从这三者中知一求二,抓住这三者结构特点,有关这三者题型的升华,以及相关实际应用问题提炼这几方面加以说明.
三角函数;“会而易错”的问题
说到三角函数中的sinα+cosα、sinα-cosα、sinαcosα这三者关系,大家一定并不陌生,因为它们通过sin2α+cos2α=1这个平方关系式紧密连在一起,构成一个不可分割的整体.这部分内容总体比较简单平稳,学生理解起来难度并不大.但从实际考试情况来看,情况又不容乐观,经常出现增解,或者由于说理不透而无谓失分,非常可惜.本文通过以下几个典型的例子来说明错误的原因以及注意事项,尽量杜绝会而常错现象.
一、三者关系中知一求二
条件求值是数学中很重要的题型,给出某些已知条件,然后会让学生求与条件相关的一些结论,即考查知识的相通性.有些可以通过定理、公式、结论等很快得到解答,但三角中的这块内容却会做而做不对,那么,问题在哪里呢?




二、抓住三者结构特点解题
由于sinα+cosα和sinαcosα正好可以看成是二次方程的两根之和与两根之积,所以问题可与方程的根联系起来,从而可以和二次方程的根与系数的关系联合考查.

求:(1)k的值;(2) sinθ,cosθ及θ的值.

例3 求函数y=sinx-cosx-sinxcosx的值域.


三、相关实际应用问题的提炼
应用题是高考不可缺少的题型,三角应用题也会经常被考查,三角与导数相结合的应用题更加普遍,每年的模拟题中就会见到不少.
例4 (课本习题改编)一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1 m的四分之一圆弧,AB、DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1 m.

(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.
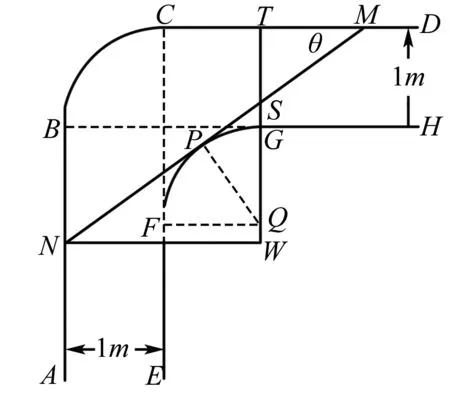
解 (1)如图,设圆弧FG所在圆的圆心为Q,过Q点作DC垂线,垂足为点T,且交MN或其延长线于点S,连结PQ,再过点N作TQ的垂线,垂足为W.
在Rt△NWS中,因为NW=2,∠SNW=θ,
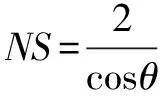

①若S在线段TG上,则TS=QT-QS.






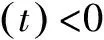
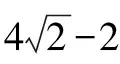
综上所述,三角函数中这三者,紧密不可分.若能掌握好知识点之间的相互关系,学生对于解决类似于例4的综合题就会更加得心应手.教学中要精心设计例题,多让学生寻找相互关系,从而更好地学好相关知识,举一反三,让自己的解题能力更胜一筹,把这类容易上手而较易失分的问题完美解答.
G632
B
1008-0333(2017)10-0048-02

