动态荷载作用下细观混凝土的尺寸效应研究

雷光宇，党发宁

(1.陕西省土地工程建设集团， 陕西 西安 710075；2.西安理工大学 岩土工程研究所， 陕西 西安 710048)

动态荷载作用下细观混凝土的尺寸效应研究

雷光宇1，2，党发宁2

(1.陕西省土地工程建设集团， 陕西 西安 710075；2.西安理工大学 岩土工程研究所， 陕西 西安 710048)

混凝土材料的尺寸效应问题是很复杂的但同时又非常重要。为了研究动态荷载作用下混凝土的尺寸效应，从数值试验出发，根据自行编制的程序，生成随机骨料模型，应用塑性损伤本构，数值计算了不同尺寸下混凝土的动态破坏强度。结果发现：在相同的加载速率下，随着试件尺寸的增大，材料的强度在增大，破坏位移也在增大；混凝土的动强度随应变率的增加而提高，当随着试件尺寸的增大时，其动强度的增大幅度更为明显。

水工材料；细观混凝土；随机骨料模型；动态荷载；尺寸效应

在土木、水利等学科中，由于研究对象的实际结构尺寸均比较大，难以进行真实结构的足尺试验，仅能进行小尺寸试件模拟，建立试验结果与实际结构的受力情况的内在关系，切实指导工程项目，是目前广大研究者的研究难点和重点，即面临着尺寸效应问题[1-3]。混凝土作为非均质准脆性材料，它的尺寸效应问题在理论上是很复杂的，但在工程上又非常重要，因此，探寻混凝土材料具有尺寸效应的内在原因，从而建立与之相应的力学模型显得尤为重要。静力作用下混凝土材料的尺寸效应研究已取得了丰硕的成果[4-6]，但是，混凝土材料在动力荷载作用下的尺寸效应研究则极为少见，Elfahal M M等[7]通过对长径比相同、直径不同的普通混凝土和高强混凝土试件进行动态荷载作用下的物理试验和数值试验，发现混凝土随着试件尺寸的增大，其动强度与试件尺寸成反比，这与在静载作用下的尺寸效应是不同的；王敏等[8]对不同尺寸的立方体混凝土试件分别进行了不同应变率下的单轴压缩试验，发现相同应变速率下混凝土的峰值应力、峰值应变均随混凝土尺寸的增大而减小，弹性模量随混凝土尺寸的增大而增大；胡伟华等[9]分析了不同试件尺寸不同应变速率下混凝土的应力-应变全曲线、吸能特性，发现混凝土在应变速率较小时，其吸能能力随应变速率的提高而增强，当应变速率超过某一值后，其吸能能力增强趋势将不显著。目前已得到的混凝土在动态荷载作用下的尺寸效应，由于试验条件的限制以及计算方法的局限性，导致并没有形成一个统一的认知。

为了克服物理试验的局限性，随着计算机硬件水平的不断发展以及混凝土本构模型的日趋完善，数值模拟混凝土的力学特性成为研究趋势[10-13]。本文尝试从数值方法入手，通过建立混凝土的随机骨料模型，数值模拟细观混凝土在不同应变率下的力学特性，以期为细观混凝土的尺寸效应研究提供帮助。

1 细观混凝土随机骨料模型

随着计算技术的发展，可将混凝土看作由骨料、水泥砂浆以及这二者之间的相交接界面组成的非均质复合性材料，基于细观力学数值分析，直观地显示混凝土试件的裂缝扩展过程及其破坏形态，深入研究其损伤破坏机理，建立数字混凝土模型至关重要。结合工程建设中混凝土的实际情况，根据骨料级配和配合比，假定骨料形状为球形，计算出给定尺寸的试件中，骨料粒径不同的颗粒的数目，应用蒙特卡洛方法计算出合适的随机数，根据FORTRAN语言自行编制相应程序，从而生成细观混凝土随机骨料几何模型，并采用“骨料投影网格”法对模型进行剖分，得到有限元计算模型[14]。

1.1 随机数的生成

混凝土试件中骨料颗粒位置的分布，是一种随机过程，运用蒙特卡罗方法求出要解决问题的各随机变量，即得到满足一定分布的随机数。

本文中，随机变量的生成采用的是混合同余法，可表示为式(1)：

Xi=(AXi-1+C)(modM)

(1)

在式(1)中，A、C、M都是正整数，其中A为乘子，C为增量，M为模。(modM)表示除以模M后取其余数。此递推公式中，需要首先给出初值X0，可推算出X1，X2，X3，…。对此数列除以模，然后取其余数，可以得到[0，1]这个区间内均匀分布的随机变量序列Ri，如式(2)所示：

(2)

选择参数时，参数必须满足以下两个条件：

(1) 增量C要大于零，而且增量C与模M互素；

(2) 乘子(A-1)必须是4的倍数。

1.2 有限元模型的生成

根据得到的随机数，生成球心坐标值，从而保证球体在空间中是随机分布的；将以上生成的随机变量，通过FORTRAN编写相应程序，以命令流的方式读入ANSYS软件中，则可得到混凝土骨料随机分布的几何模型。

对几何模型直接进行网格划分，对处理二维模型比较好，但对于三维模型来说，由于单元大小的设置要符合实际，在对骨料、砂浆以及两者的粘结面进行有限元网格剖分后，会造成单元节点数目非常多，数据量相当大。所以，需要采用一种新的网格剖分法来生成混凝土三维有限元模型，本文根据自行编制的程序，根据“骨料投影网格法”，利用随机生成的骨料球心坐标和骨料粒径，让其投影到已经进行了单元剖分但没赋予材料属性的有限元模型中，判断这些单元的节点是否在骨料粒径的范围内，依此来判断单元的材料属性。最终生成的混凝土三相材料的随机骨料计算模型如图1所示。

(a) 整体模型(b) 骨料(c) 砂浆(d) 界面

图1 混凝土三相材料计算模型

1.3 计算条件

本文研究中，不同尺寸的构件是几何相似的，主要分析不同骨料尺寸与试件尺寸相对变化对混凝土试件强度的影响。计算中采用ABAQUS中的混凝土塑性损伤模型，该模型引入了损伤概念，能很好地描述混凝土在动力荷载作用下的力学行为。

分别建立直径为20mm，高为40mm；直径为40mm，高为80mm；直径为60mm，高为120mm；直径为80mm，高为160mm4种不同尺寸的混凝土圆柱体试件，根据大岗山拱坝工程的实际配合比(水∶水泥∶粉煤灰∶砂∶石=86∶134∶57∶548∶1607)以及骨料颗粒的粒径大小，采用粒径D为10 mm～12 mm的一级配骨料，计算过程中，取其平均粒径11 mm，混凝土各相组分材料特性力学参数按表1取值。4种混凝土圆柱体试件的骨料个数依次为10、82、278、656。模型截面如图2所示。

表1 混凝土三相组分材料各参数

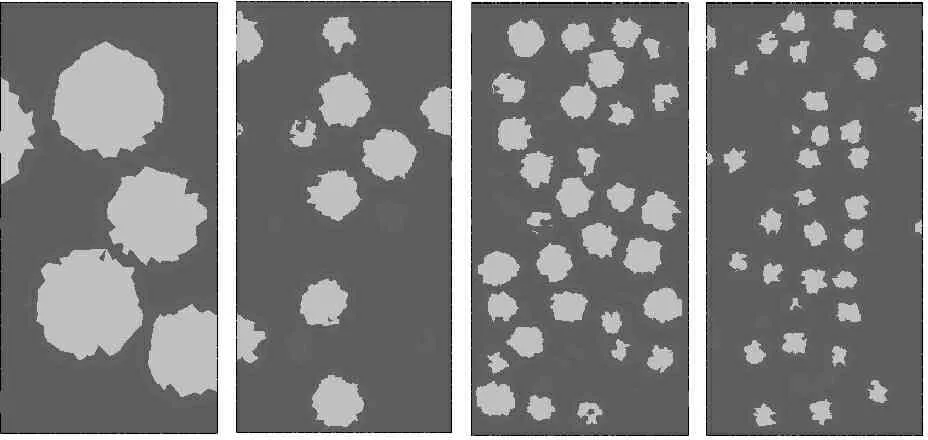
(a) 试件1(b) 试件2(c) 试件3(d) 试件4

图2 不同试件尺寸模型截面图

对不同尺寸模型分别施加相同的动压荷载，应变率分别为2.00/s、0.60/s、0.08/s，其它条件不变，令尺寸效应比例系数L=试样直径/骨料粒径，即：

L1=20mm/11mm

L2=40mm/11mm

L3=60mm/11mm

L4=80mm/11mm

对该计算模型施加如图3所示的约束，圆柱体模型底面施加Z向约束，上下底面边沿位置施加X、Y向约束。

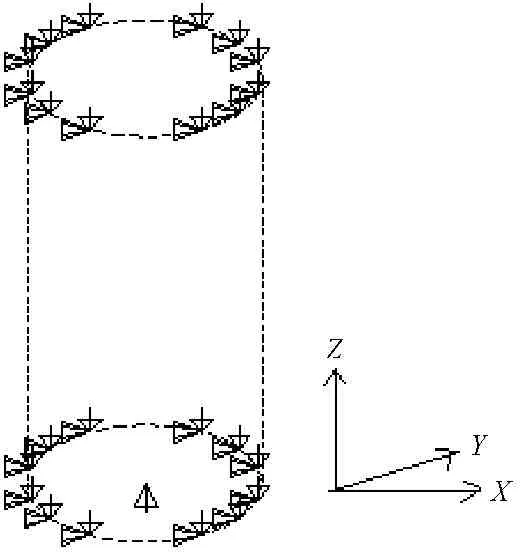
图3 模型约束图

2 动态荷载作用下混凝土破坏强度的数值试验确定方法

由于混凝土材料组成复杂，结构不均匀，变异性又较大，因而还没有一种强度理论或模型能圆满地解释混凝土在不同受力条件下的破坏现象。因而针对各种单一的受力状态直接由试验得出强度值仍是结构设计和应力分析的重要依据，但是由于试验条件等原因的影响，这些因素都在不同程度上影响混凝土的真实抗压强度。

描述材料破坏主要有三种方法：应变或位移、能量及动力学方法。对于混凝土结构，破坏首先意味着其结构整体不能继续承受外部荷载的增加；其次破坏裂纹贯通形成整体的破坏面，沿破坏面两侧会出现显著的、较大规模的相对位移，从而会导致位移出现突变。所以，通过研究荷载位移曲线上的峰值点和位移突变点这两个特征，可以判断混凝土试件是否发生破坏。

作者在文献[15]从破坏的特征出发，思考从荷载位移曲线峰值点和位移突变点进行研究，对比分析荷载和位移之间的关系，发现混凝土材料发生破坏时，其两个特征至少会出现一个。并提出可以通过判断荷载位移曲线突变点作为混凝土发生破坏的依据，根据数值试验和CT物理试验结果对比分析，以位移控制加载得到的荷载位移曲线的拐点作为试件的破坏点，相对应的荷载值作为试件发生破坏时的强度，即试件的破坏强度。

本文计算中，施加位移加载方式，以荷载位移曲线强度出现拐点，即峰值点处的强度作为混凝土在动态荷载作用下的破坏强度。

3 动态荷载作用下混凝土的尺寸效应研究

3.1 不同加载速率下混凝土的尺寸效应

计算得到不同应变率下，尺寸效应比例系数与试件强度的关系曲线如图4所示，在动荷载作用下，在相同的加载速率下，不同尺寸的试件，其破坏强度是不一样的，在一定的试件尺寸范围内，随着尺寸效应比例系数的增大，即试件直径与骨料粒径比值越大，试件的强度就越大，这与静载作用下，混凝土的强度随着试件尺寸的增长而减小恰恰相反。试件强度与试件尺寸并不成等比例增长，在尺寸较小时，试件强度随尺寸增大的幅度较小，试件强度增加的幅度随着尺寸的逐渐增大，也在逐渐提高。在不同的加载速率下，应变率不同，不同尺寸的混凝土试件其破坏强度随应变率的变化幅度也不尽一样，总体来看随着试件尺寸的增大，不同应变率下的试件破坏强度都在增大，但是，随着应变率的降低，混凝土试件的破坏强度增加幅度却在减小，试件尺寸比较小时，试件在不同的应变率下的破坏强度变化比较小，而当试件尺寸逐渐增大时，各自试件在不同的应变率下的破坏强度变化逐渐增大，即混凝土的动强度在应变率增大时，随着试件尺寸的增大时，其动强度的增大幅度更为明显；而当应变率降低时，其动强度的增大幅度却在减小，说明混凝土的尺寸效应受材料率效应和惯性效应的影响。

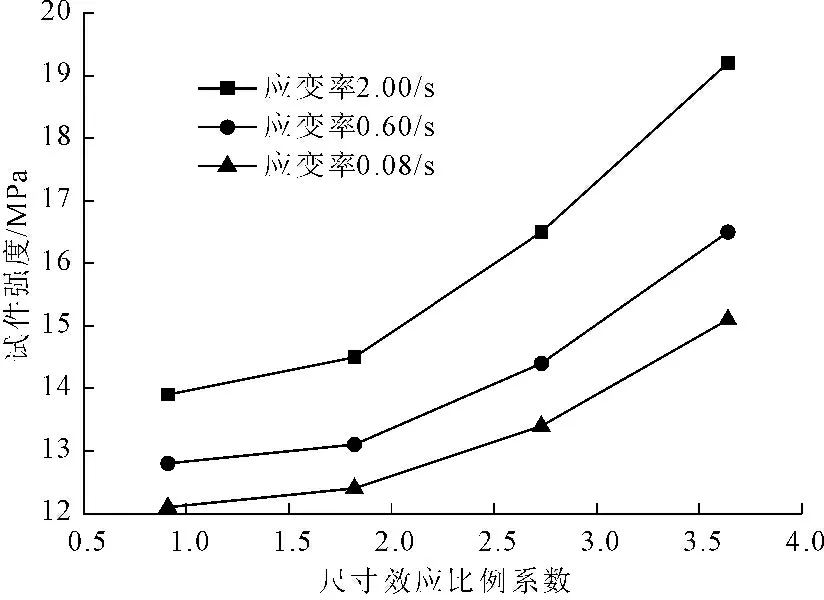
图4 不同应变率下混凝土破坏强度与试件尺寸关系图

从不同应变率下不同尺寸混凝土的破坏位移图5看，在相同的加载速率下，在一定的尺寸范围内，随着试件尺寸的增大，其破坏时的位移也在增加，两者呈线性增长关系。在一定的尺寸范围内，不同的加载速率下，混凝土的破坏位移随着加载速率的提高，也在增大，但是当应变率在一定的范围内时，由于是位移加载，由于计算步长的原因，破坏位移不随应变率变化。

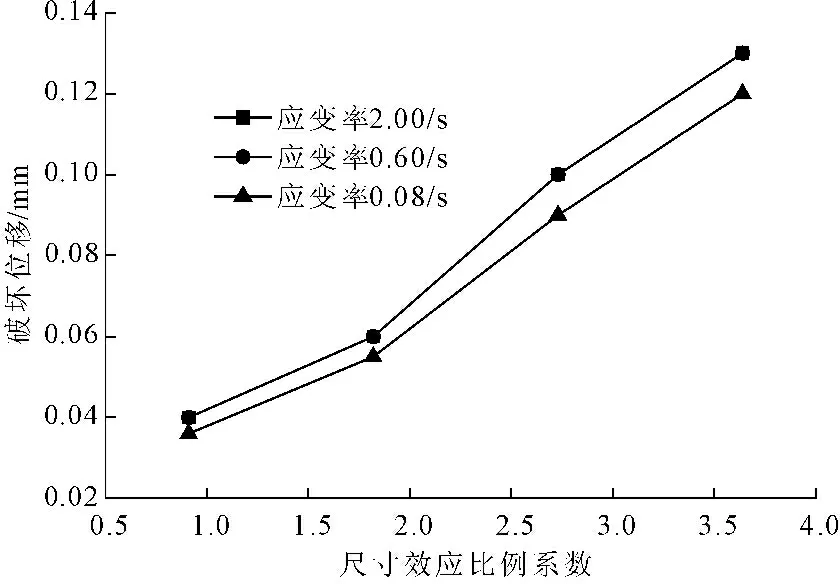
图5 不同应变率下混凝土破坏位移与试件尺寸关系图

3.2 不同试件尺寸对混凝土动力特性的影响

混凝土材料的尺寸大小，对其力学特性有很重要的影响。在静力荷载作用下，混凝土的强度随着试件几何尺寸的增大而减小，当几何尺寸增大到一定尺寸时，试件的强度趋于稳定。这主要是因为在静力荷载作用下，当骨料尺寸不变，试件的尺寸较小时，混凝土试件直径与骨料半径相比较小时，此时，材料的非均匀性明显，材料中的骨料占主导作用，材料的强度就偏大，当试件尺寸变大后，材料的非均匀性降低，材料中的砂浆占主导地位，材料的强度就偏小，随着试件的尺寸不断增大，材料越接近于均质体，所以，材料的强度趋于稳定。同时，作为非均质复合材料，粘结界面是混凝土的薄弱环节，缺陷往往发生在界面处，静力破坏时，损伤常常从界面处开始萌生，发展，最后，沿着界面发生破坏，当试件尺寸较小时，界面含量少，所以，缺陷的概率就低，固不容易发生破坏，所以试件的强度大，当试件的尺寸增大后，界面含量高，所以，缺陷的概率就大，固相对容易发生破坏，试件的强度就小。

而混凝土在动力荷载作用下的尺寸效应不同于静力作用下的尺寸效应，其产生机理和原因极其复杂，目前并没有完全研究清楚，但是可以确定的是，混凝土材料在动、静荷载作用下的尺寸效应变化规律不同，究其原因，主要是由材料的率效应和惯性效应两个方面引起的。动力作用下，混凝土的强度受惯性力作用比较明显，惯性力大，试件强度大，而混凝土的试件尺寸大了，其惯性力也大，所以，在相同的加载速率下，试件大的，其强度提高也大；在试件尺寸相同时，加载速率大的，其惯性效应越明显，所以其破坏强度也大。混凝土试件尺寸对其动强度的影响随着应变率的提高而增强，这是与静载条件下的尺寸效应相反，所以推测可能存在一个临界的应变率，低于该临界应变率时，主要表现为静载的尺寸效应，高于该临界应变率时，则主要表现为动载的尺寸效应。

同时，由于动力作用下，其破坏形态与静力有所区别，静力作用下，破坏绕最薄弱部位发展，所以容易在界面发生，而动力作用下，破坏沿最短路径发展，所以容易穿过骨料，界面的多少对混凝土的动强度影响变小，而大试件的惯性力大于小试件的惯性力，所以，大试件的混凝土比小试件的混凝土强度大，即，一定的试件尺寸范围内，随着混凝土试件尺寸的增大，在相同的加载速率下，随着试件尺寸的增大，材料的强度也在增大。

4 结 论

(1) 本文建立的混凝土随机骨料模型适合于动荷载作用下的尺寸效应研究，为进一步研究细观混凝土的动态力学特性奠定了基础。

(2) 在相同的加载速率下，随着试件尺寸的增大，材料的强度在增大，破坏位移也在增大；混凝土的动强度随应变率的增加而提高，当随着试件尺寸的增大时，其动强度的增大幅度更为明显。

(3) 一定的试件尺寸范围内，混凝土动载作用下的尺寸效应，主要由材料的率效应和惯性效应两个方面引起的。

[1] 杨 钻.混凝土尺寸效应的细观数值分析及试验研究[D].长沙:湖南大学,2009.

[2] 谭 彩，吴 勇，万 里，等.无黏性粗粒土强度的三轴尺寸效应[J].江南大学学报(自然科学版),2015,14(6):810-813.

[3]VisoJRD,CarmonaJR,RuizG.Shapeandsizeeffectsonthecompressivestrengthofhigh-strengthconcrete[J].CementandConcreteResearch, 2008,38(3):386-395.

[4] 苏 捷,方 志，杨 钻.骨料组分和强度等级对混凝土单轴受压性能尺寸效应的影响[J].建筑结构学报,2014,35(5):120-127.

[5] 杜 敏,杜修力，金 浏，等.混凝土拉压强度尺寸效应的细观非均质机理[J].土木建筑与环境工程，2015,37(3):11-18.

[6] 党发宁,梁昕宇,田 威，等.混凝土随机骨料模型尺寸效应的细观数值分析[J].岩土力学，2009,30(S2):518-523.

[7]ElfahalMM,KrauthammerT,OhnoT,etal.Sizeeffectfornormalstrengthconcretecylinderssubjectedtoaxialimpact[J].InternationalJournalofImpactEngineering, 2005,31(4):461-481.

[8] 王 敏，彭 刚，田 为，等.混凝土尺寸效应的动态率相关性试验研究[J].中国农村水利水电，2014(6)：176-179.

[9] 胡伟华，邹荣华，彭 刚，等.不同应变速率下混凝土吸能特性及尺寸效应的研究[J].长江科学院院报，2015,32(5)：132-136.

[10] 雷光宇，韩霁昌，党发宁，等.预静载对细观混凝土动态力学特性的数值试验研究[J].水利与建筑工程学报，2016,14(3):55-58.

[11] 唐欣薇，石建军，郭长青，等.自密实混凝土强度尺寸效应的试验与数值仿真[J].水力发电学报，2011,30(3):145-151.

[12] 屈彦玲，彭一江，杜立峰.碾压混凝土试件抗剪强度尺寸效应的数值模拟[J].水利与建筑工程学报，2007,5(3):22-24.

[13] 王立成，邢立坤，宋玉普.混凝土劈裂抗拉强度和弯曲抗压强度尺寸效应的细观数值分析[J].工程力学，2014,31(10):69-76.

[14] 党发宁，韩文涛，田 威，等.混凝土单轴压缩破坏过程的三维细观数值模拟[J].西安理工大学学报，2006,22(2):113-118.

[15] 雷光宇，党发宁，陈厚群.冲击荷载作用下混凝土破坏强度的确定及CT验证[J].地震工程与工程振动，2013,33(3):162-168.

Size Effect of Meso Concrete Under Dynamic Load

LEI Guangyu1，2, DANG Faning2

(1.ShaanxiLandEngineeringConstructionGroup,Xi'an,Shaanxi710075,China;2.InstituteofGeotechnicalEngineering，Xi'anUniversityofTechnology,Xi'an,Shaanxi710048,China)

Size effect of concrete materials is very complex and very important. In order to study the size effect of concrete under dynamic load, the numerical experiments were adopted in this research. Based on a program developed by the author a random aggregate generation model was developed. Based on the plastic damage constitutive theory the dynamic breaking strength of concrete at different sizes was numerically analyzed. The results show that at the same loading rate, with the increase of sample size the strength of the material in increasing damage displacement also increased. The dynamic strength of concrete increases with the strain rate increase. Its dynamic strength increases significantly with the sample size increases.

hydraulic material; meso concrete; random aggregate model; dynamic load; size effect

10.3969/j.issn.1672-1144.2017.02.018

2016-11-28

2017-01-10

退化及未利用土地整治创新团队项目(2016KCT-23)

雷光宇(1984—)，男，陕西渭南人，博士，工程师，主要从事混凝土力学特性等方面研究。E-mail:leiyugogo@163.com

TU37；TV

A

1672—1144(2017)02—0096—04