导弹系统振动频率自适应估计方法与仿真

张 衡， 芮筱亭， 杨富锋， 陈刚利

(南京理工大学 发射动力学研究所，南京 210094)

导弹系统振动频率自适应估计方法与仿真

张 衡， 芮筱亭， 杨富锋， 陈刚利

(南京理工大学 发射动力学研究所，南京 210094)

为了提高处于导弹高过载、强冲击、大振动复合动态环境中捷联惯组的输出精度，设计了级联型二阶自适应陷波滤波器来估计导弹的弹性振动频率。该滤波器采用带有遗忘因子的递推最小二乘法实时优化每个陷波滤波器的参数,具有计算复杂度低，收敛速度快等特点。仿真和实验结果表明，此方法对于处在复合动态环境中导弹振动信号的频率估计效果较好，且具有较好的抗噪声干扰能力，适合弹上计算机进行实时计算。

自适应陷波滤波器；频率估计；递推最小二乘法

导弹发射与飞行过程中，随着燃料不断消耗，质量和刚度分布将不断变化，引起导弹弹性振动频率随飞行时间的函数不断变化。捷联式惯组的陀螺仪和加速度计直接固联在导弹上，振动将传递到惯组器件上，引起陀螺仪质心偏移和结构变形，使惯性器件产生动态测量误差。当惯组工作频率接近其共振频率时，将造成惯组动态精度大幅下降或者永久性破坏甚至输出完全错误的信息，从而导致导弹完全失控。因此，设计一个适用于弹上非平稳信号的频率的实时估计的算法非常重要。

频谱估计是数字信号处理的主要内容之一，传统的方法是基于快速傅里叶变换(FFT)，但它的估计性能不高，因为FFT的频率分辨率仅与数据序列的长度有关，要提高FFT算法的分辨率只能靠增加采样时间来实现，这在许多场合下尤其对于导弹的飞行过程来说是不允许的。现代谱估计算法中的参量法具有估计精度高和分辨率高的特性，但参量法谱估计的高分辨率和高精度特性只能在高信噪比条件下才能实现[1]。导弹飞行的主动段、自由飞行段以及再入段的某些瞬间的冲击信号或干扰可能会对惯组产生很大的影响，因此如何分析和捕获这些瞬态分量，对其进行有效的分析对于弹用惯组的自适应减振系统的设计、制造和维护具有重要意义。

在许多应用中，正弦信号可能受到非线性的影响，其中可能会产生谐波频率分量。在这样的环境下，我们想要估计信号的基频以及任何谐波频率，采用单个二阶陷波滤波器去估计基频与谐波的频率是不够的，因为它只能容纳一个频率分量。另一方面，应用高阶无限脉冲响应(IIR)滤波器可能效率不高，由于它采用多个自适应滤波器系数[2]。因此，本文采用将二阶自适应陷波滤波器级联的方法进行导弹频率的实时估计，该滤波器采用递推最小二乘法实时优化每个陷波滤波器的参数,具有计算复杂度低，收敛速度快等特点。结果表明，该方法对于处在复合动态环境中导弹振动信号的频率估计效果较好，且具有较好的抗噪声干扰能力。

1 导弹弹性振动模型

导弹主动段飞行是在推力T的作用下做加速运动，此时，导弹受到均匀的分布惯性力。导弹具有较大的长径比，且各个部分的质量分布及刚度分布不同，因此，将导弹看成由n段Euler-Bernoulli梁组成，每段梁都具有均匀的线密度和弯曲刚度。由于受到惯性力的作用，每段梁所受到的轴向力沿轴向呈不均匀分布。采用多体系统传递矩阵法建立导弹动力学模型，如图1所示。梁微段受力分析，如图2所示。

图1 导弹动力学模型Fig.1 The missile dynamic model

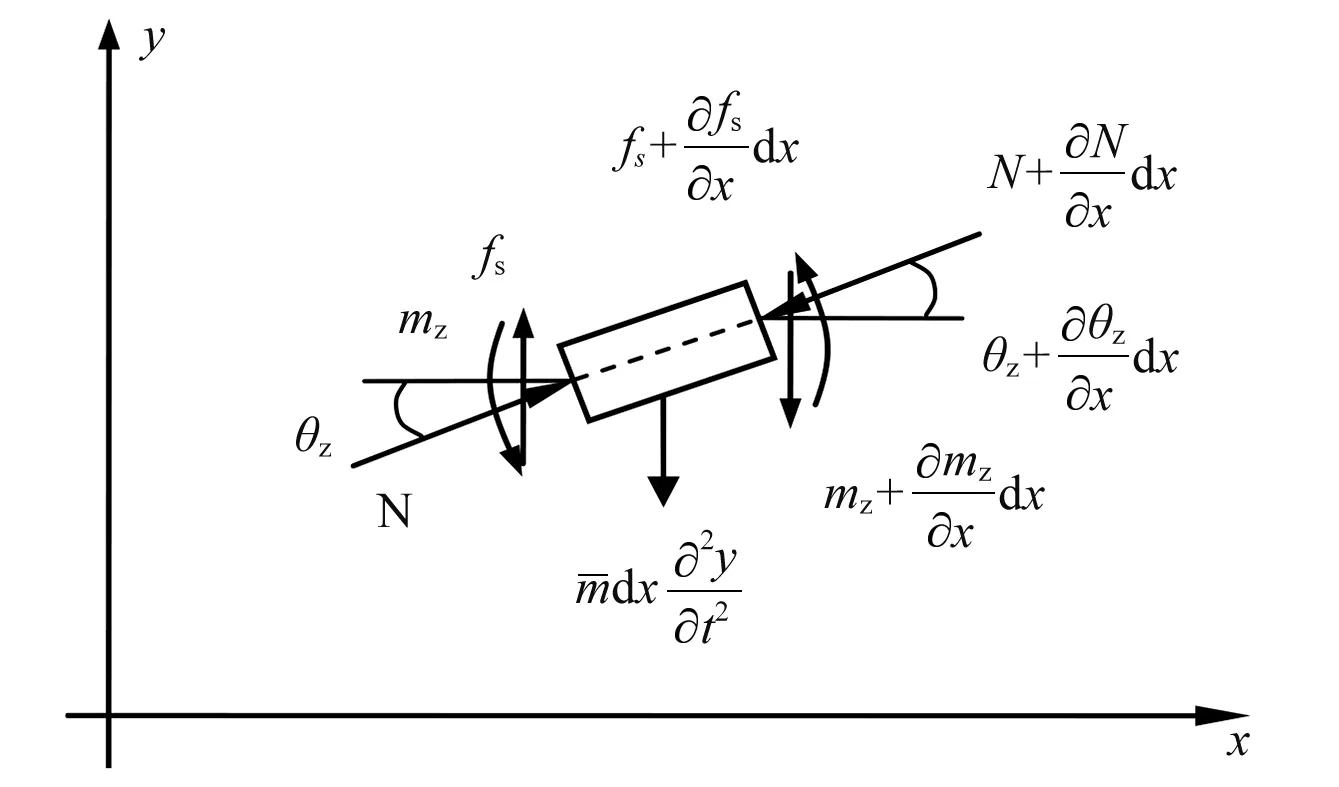
图2 梁微段受力分析Fig.2 The force analysis of the sub-beam

对图2所示的梁微段进行受力分析，梁微段dx沿

横向所受的外力有：剪力fs(x)和-fs(x+dx)，轴向力N(x)和-N(x+dx)在轴上的投影。

根据牛顿第二定律，忽略二阶小量，梁微段横向运动满足

(1)

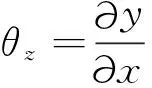
(2)

此方程为一个非线性偏微分方程，这里将梁分为多段，每一段的轴向力视为常力处理，则梁的弯曲自由振动方程为

(3)

这是一个常系数的齐次线性偏微分方程。令y(x,t)=Y(x)eiωt，代入上式得

(4)

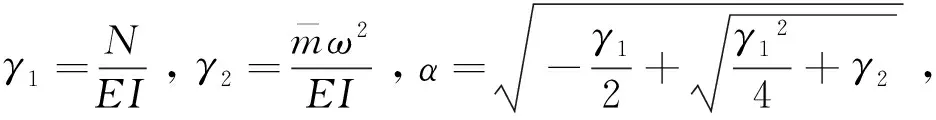
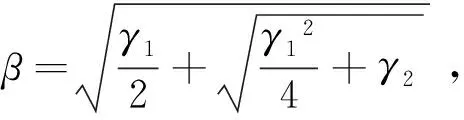
Y(x)=Acoshαx+Bsinhαx+
Ccosβx+Dsinβx

(5)

对Euler-Bernoulli梁，将Θz,Mz,Qy的表达式写成矩阵形式可以得到

Z(x)=B(x)a

(6)

式中，Z(x)=[YΘzMzQy]Tx为状态矢量，a=[A,B,C,D]T

(7)

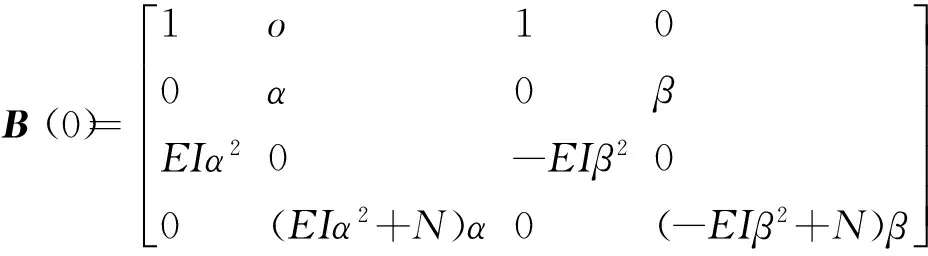
(8)

所以受轴向力Euler-Bernoulli梁的传递矩阵为

(9)

由各段梁的传递方程可以得到系统的总传递方程为

Zn,n+1=UnUn-1…U2U1Z1,0=UallZ1,0

(10)

系统总传递矩阵为

(11)

系统的边界条件为

(12)

代入式可以得到

(13)

删去与零元素有关的行和列可以得到

(14)

式中

上式存在非零解，则

(15)

由上式可求得α和β，也即得到γ1和γ2，由γ2得到对应的ωp(p=1,2,…,n)及其对应的增广特征矢量Vp(p=1,2,…,n)。从而可求解出广义坐标qp(t)(p=1,2,…,n)，以及导弹的动力响应ν。

导弹的广义坐标为

(16)

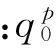
导弹的动力响应为

(17)

2 导弹振动频率估计方法

在传统的信号处理中，分析处理信号最常用的方法是Fourier变换，但是它针对的是周期性平稳信号，依赖信号的全局信息，并不能反映信号的局部特征，故对分析非平稳信号不具有效性[4]。对于导弹的发射与飞行过程，振动信号是非平稳信号，针对其特点，本文采用将二阶自适应陷波滤波器级联的方法来处理。

图3给出了自适应滤波器的一般结构，其中，x(k)表示输入信号。y(k)为输出信号，d(k)表示期望信号，误差信号e(k)=d(k)-y(k)。

由数字滤波器设计的一般原则,陷波器的设计有两个基本要求:

一是其传递函数的零点应在单位圆上，以使陷波的陷阱深度为无穷大。满足这一要求的多项式的系数应具有镜像对称的形式，如下式所示A(z-1)=1+a1z-1+a2z-1+…+anz-1+…+a1z-1+z-2n

(18)

式中，z是复数变量，n为陷波个数，当考虑单个陷波时n=1，上式变为

A(z-1)=1+a1z-1+z-2

(19)

第二个基本要求是其传递函数的极零点必须匹配，这样除了陷波的频率之外，其余的频率完全不受陷波的影响。综合这两个基本要求，若在单位圆上频率ω0处设置一对半径r=1的共扼零点，同时在单位圆内同样频率ω0处设置一对半径为ρ(0≤ρ<1)的共扼极点，将会产生一个幅频特性在ω0处强烈衰减，而在其他频率成分处信号基本不受影响的陷波器。

如图4为级联型的二阶陷波滤波器的计算流程图。

图4 级联型二阶陷波滤波器计算流程图Fig.4 The calculation flow chart of cascade of second-order notch filters

Z域上二阶陷波滤波器形式[5]为

(20)

式(20)中的滤波器结构难以进行自适应陷波滤波计算，为此选用基于Regalia[6]提出的自适应陷波滤波器，形式为

(21)

式(20)与式(21)形式保持一致可得到β0(1+β1)=ρa(1+b)，可化为

β0=ρa(1+b)/(1+ρ2b)

为得到自适应陷波滤波器，参数的数目应保持最小。如果我们假设ρ等于1，

β1=ρ2b≅ρb
β0(1+β1)=ρa(1+b)≅a(1+ρb)

(22)

因此，β0=a成立，Regalia提出的方程可改写为

(23)

一般地，当零点位于单位圆上时，能保证陷波滤波器有更好性能。因此，在式(23)中，参数b等于1，它可以简化为一个下列形式的关于ρ和a的函数：

(24)

其中，ρ位于0.9和0.99之间，如果它接近1，滤波器的带宽变窄。

陷波滤波器的输入信号，记为U(n)。然后每个部分的输出信号可以表示为

(25)

对于级联型陷波滤波器，式(25)被下式取代

yk(n)=xk(n)+xk(n-2)+2akxk(n-1)

(26)

式中，xk(n)表示通过滤波器的分母的信号。为了设计自适应算法，提出优化的损失函数如下

(27)

如式(28)～(30)显示的递推最小二乘[7]法是用来估计未知参数向量θ=[a1…ap]T。时间平均自相关φk(n)和时间平均互相关αk(n)由下式给出[8]

φk(n)=λφk(n-1)+A2(n)

(28)

αk(n)=λαk(n-1)+A(n)·B(n)

(29)

其中A(n)=2xk(n-1),B(n)=xk(n)+xk(n-2)

k阶段的估计参数由下式给出

ak(n)=-φk(n)-1αk(n)

(30)

由于陷波极点位于单位圆内，所以参数ak也在范围ak∈[-1,1]。因此，导弹的振动频率可以使用采样时间ΔT估计为如下[9]

(31)

3 仿真结果及实验验证

3.1 仿真结果

为验证算法的频率估计效果，特以某型导弹为例，对其主动段飞行过程进行仿真，用自适应二阶陷波滤波器级联的方法对多体系统传递矩阵法计算得到的响应数据进行频率的估计。首先，用多体系统传递矩阵法计算得到导弹的振动频率ωp(p=1,2,…,n)及其对应的增广特征矢量Vp(p=1,2,…,n)，从而可求解出广义坐标qp(t)(p=1,2,…,n)以及导弹的动力响应ν，其中，导弹的动力响应的计算如式(17)所示。然后，用本文提出的自适应二阶陷波滤波器级联的方法对多体系统传递矩阵法计算得到的导弹的动力响应进行频率的估计。由于一阶模态对系统动力响应的影响最大，本文仅以识别导弹一阶频率为例，验证此算法的有效性。

通过多体系统传递矩阵法计算得到导弹的动力响应，如图5所示。分别通过多体系统传递矩阵法计算得到的导弹主动段的振动频率变化曲线和通过自适应二阶陷波滤波器级联的方法估计得到的导弹主动段的振动频率变化曲线的对比，如图6所示。

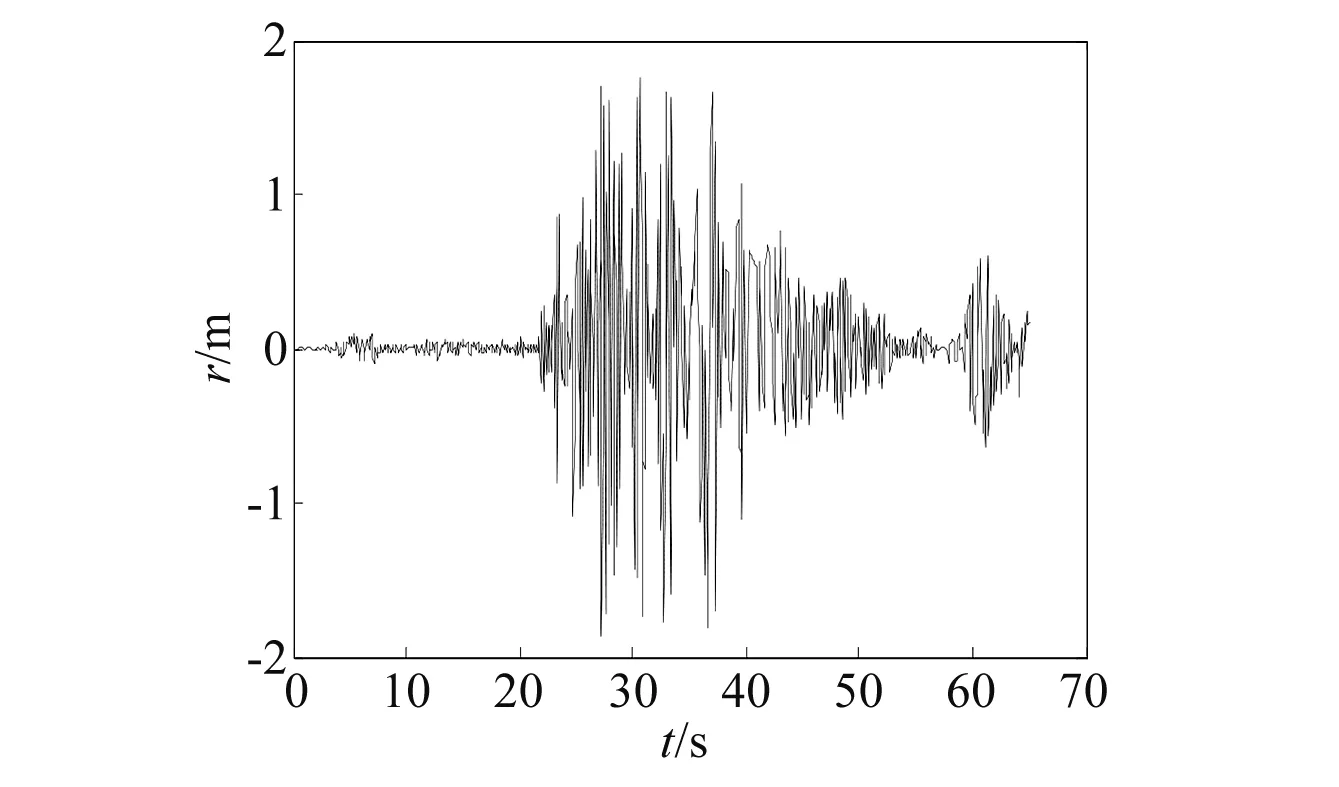
图5 通过多体系统传递矩阵法计算得到的动力响应Fig.5 The dynamic response of the missile calculated by the transfer matrix method of multibody system

图6 分别用多体系统传递矩阵法计算得到的与用自适应二阶陷波滤波器级联的方法估计得到的导弹主动段振动频率曲线的对比Fig.6 The vibration frequency curve of the missile in the boost phase obtained respectively by using the transfer matrix method of multibody system compared with the method of cascade of second-order adaptive notch filters

由图6可清楚的看到，用本文提出的用自适应二阶陷波滤波器级联的方法估计得到的导弹振动频率结果与多体系统传递矩阵法计算得到的导弹振动频率结果非常接近。仿真结果表明，该方法对于导弹的振动频率估计效果较好，符合预期效果。

3.2 实验验证

导弹在主动段、再入段飞行中受到发动机推力、喷气噪声以及紊流边界层压力等综合作用产生的宽频带、大幅值振动激励。测试表明某导弹飞行的振动环境所对应的频率范围为20～2 000 Hz。

为进一步验证该算法的频率估计效果，用振动台模拟导弹振动的环境，做了捷联于它的惯组的振动实验，实验现场如图7所示。图8为振动台扫频幅值时间历程，图9为振动台20～2 000 Hz扫频频率估计曲线。导弹发射、飞行的整个过程，频率范围基本在20～2 000 Hz，因此选定振动台扫频的范围为20～2 000 Hz。从图9可看出来，该扫频实验的频率估计结果与实际情况一致，估计曲线比较平滑。

图7 捷联惯组的振动台实验Fig.7 The shaking table experiment of the SIMU

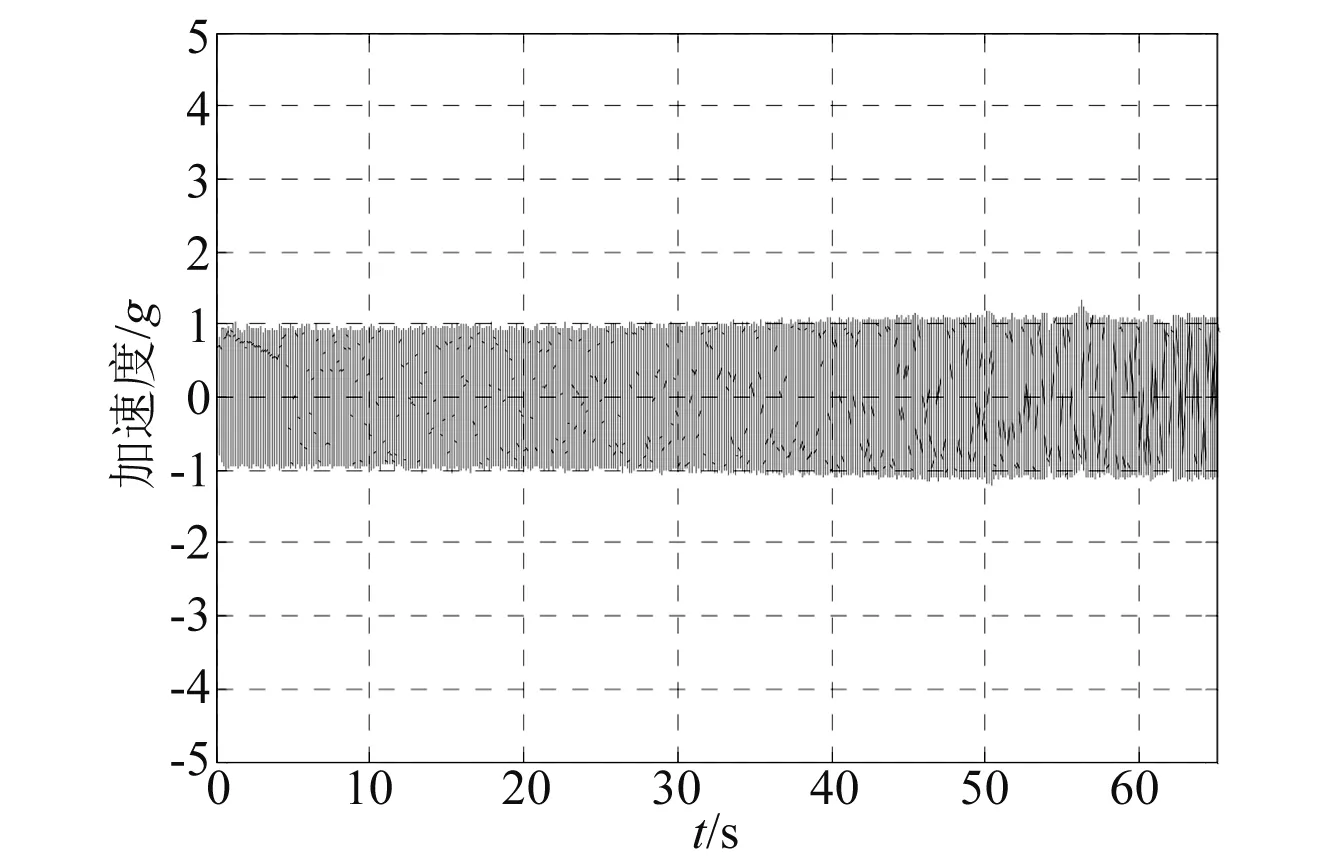
图8 振动台扫频幅值时间历程Fig.8 The time history of the sweep frequency amplitude of the shaking table

4 结 论

基于多体系统传递矩阵法，从系统动力学角度建立了导弹系统的弹性振动模型，并计算出导弹系统的振动频率以及动力响应。

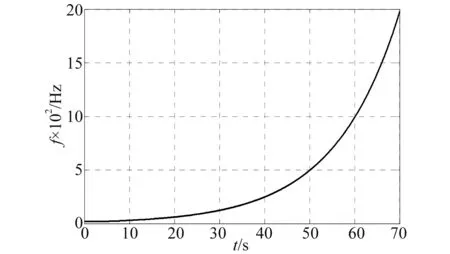
图9 振动台20～2 000 Hz扫频频率估计曲线Fig.9 The estimation curve of sweep frequency of shaking table whose range is 20～2 000 Hz

针对直接固联在导弹上的捷联惯组处于导弹高过载、强冲击、大振动复合动态环境中，输出精度差的问题，设计了将二阶自适应陷波滤波器级联的方法来估计导弹弹性振动频率，仿真和实验结果表明，该方法对于导弹振动信号的频率识别效果较好，为下一步捷联惯组的振动控制提供了依据。本文的研究为提高捷联惯组的使用精度提供了理论和技术参考。

[1] 刘洋.飞机发动机振动信号数字处理与分析技术研究[D].哈尔滨：哈尔滨工业大学，2008.

[2] TAN L, JIANG J. Novel adaptive IIR filter for frequency estimation and tracking[J]. IEEE Signal Processing Magazine,2009(11):186-189.

[3] 芮筱亭，贠来峰，陆毓琪，等.多体系统传递矩阵法及其应用[M].北京：科学出版社，2008.

[4] 张晓菲，刘振兴，陈栋.频率估计综述[J].信息技术,2011(11):58-62.

ZHANG Xiaofei,LIU Zhenxing, CHEN Dong. Summary of Frequency Estimation[J].Information Technology, 2011(11):58-62.

[5] RAO D V, KUNG S Y. Adaptive notch filtering for the retrieval of sinusoids in noise[J].Signal Processing, 1984,32(4): 791-802.

[6] REGALIA P A. An improved lattice-based adaptive IIR notch filter[J].Signal Processing,1991, 39(9):2124-2128.

[7] 单东升,张培强,吴耀武,等.基于递推最小二乘法的炮控系统参数辨识仿真[J].系统仿真学报, 2013,25(8):1726-1729.

SHAN Dongsheng, ZHANG Peiqiang, WU Yaowu, et al. Simulation of parameter identification for gun control system based on RLS [J].Journal of System Simulation, 2013,25(8):1726-1729.

[8] 李湘清,孙秀霞,王栋,等.递推最小二乘法在LQR参数调整中的应用[J].弹箭与制导学报，2007,27(4):99-101.

LI Xiangqing, SUN Xiuxia, WANG Dong, et al. LQR parameter regulate using the recursive least square[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(4):99-101.

[9] CHOI H D, BANG H C. An adaptive control approach to the attitude control of a flexible rocket[J]. Control Engineering Practice, 2000, 8(9):1003-1010.

Adaptive estimation and simulation on the vibration frequency of missile system

ZHANG Heng,RUI Xiaoting,YANG Fufeng,CHEN Gangli

(Institute of Launch Dynamics, Nanjing University of Science & Technology, Nanjing 210094, China)

To improve the output accuracy of inertial measurement unit working in the complex dynamic environment of missiles which is of high acceleration, strong impact and severe vibration, a cascade of second-order adaptive notch filters was designed to estimate the elastic vibration frequency of missiles. The recursive least square method was adopted in the filters and a forgetting factor was introduced to optimize the real-time parameters of each notch filter. The filters possess the characteristics of low computational complexity and fast convergence speed. The results of simulation and experiment show that the method has a good frequency estimation effect on the vibration signals processing of missiles in complex dynamic environment. It has a strong anti-noise ability, and is suitable for the real-time calculation of missile computers.

adaptive notch filter; frequency estimation; recursive least square method

高校博士点基金博导类：复杂多体系统变参数自适应控制方法(20133219110037)

2016-04-01 修改稿收到日期： 2016-09-09

张衡 男，博士，1985年5月生

芮筱亭 男，博士，教授，博士生导师,1956年8月生 E-mail:ruixt@163.net

TJ760.1

A

10.13465/j.cnki.jvs.2017.10.034