基于不同工况下辅助数据集的齿轮箱故障诊断

段礼祥，谢骏遥，王 凯，王金江

(中国石油大学(北京) 机械与储运工程学院， 北京 102249)

基于不同工况下辅助数据集的齿轮箱故障诊断

段礼祥，谢骏遥，王 凯，王金江

(中国石油大学(北京) 机械与储运工程学院， 北京 102249)

针对变工况下齿轮箱监测数据重用性低，受复杂工况影响大和已训练模型经常失效的问题，提出基于不同工况下辅助数据集的迁移成分分析方法用于设备故障诊断。迁移成分分析(Transfer Component Analysis, TCA)通过核函数将训练样本与测试样本映射到潜在空间，进而减小训练样本与测试样本的分布差异性。重点对比分析训练数据中不同工况下辅助数据所占比例对迁移成分分析算法性能的影响，通过仿真分析和实验验证得出，迁移成分分析方法相比传统机器学习算法，明显地减小了训练样本与测试样本的分布差异，具有更高的监测数据重用率与更高的诊断准确率，有效提高了齿轮箱变工况故障诊断的准确率和可靠性。

齿轮箱；不同工况；辅助数据集；故障诊断；迁移成分分析

齿轮箱作为动设备群中最为常见的传动部件，其内部件如轴承、齿轮制造安装精度高，经常在重载高速等复杂工况下连续运转，因此其故障率往往较高[1-3]。近年来，国内外研究学者在齿轮箱信号特征提取与分析、基于人工智能的故障诊断技术，以及故障预测模型等方面做了大量工作。然而，研究多基于实验室受控实验条件，现场工作环境恶劣，工况复杂多变(变转速、变载荷)使得采集数据不平稳、故障特征动态变化，从而导致原有基于稳定工况下的故障诊断方法不再适用。此外，复杂工况下齿轮箱的失效形式和故障类型也存在较大不确定性，进而增大了对其故障诊断的难度。目前，齿轮箱变工况故障诊断逐渐成为故障诊断领域的研究热点，国内外学者对此做了大量工作，如提出了瞬时功率谱和遗传基因算法，阶次跟踪方法，混沌和取样积分技术[4]，小波包分析[5]等，但训练样本和测试样本随工况和时间变化，分布不再满足同一分布。传统机器学习对测试样本和训练样本要求满足同一分布，据此本文提出了基于迁移成分分析的故障诊断方法。

本文讨论了不同工况下辅助数据集下的迁移成分分析方法，该方法通过核变换将训练样本与测试样本映射到潜在空间，减小了测试样本与训练样本的分布差异。最后通过仿真实验和真实实验，验证了迁移成分分析方法较传统机器学习算法(如KPCA、PCA)在不同工况下辅助数据集不同比例的情况下，均保持了更高诊断准确率，可以明显提高历史监测数据的重用率以及齿轮箱故障诊断准确率。

1 迁移成分分析理

如图1所示，迁移学习不再局限于传统机器学习对测试数据与训练数据同一分布的要求，作为一种跨领域、跨任务的学习方法[6-7]，已成功应用于文本处理[8]、图像分类[9]、人脸识别[10]、语音识别[11]、信号处理[12]与建模分析[13-14]等领域。

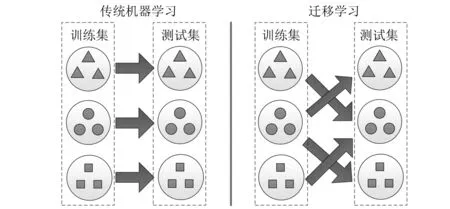
图1 传统机器学习和迁移学习比较Fig.1 Comparison of traditional machine learning and transfer learning

迁移成分分析算法是2010年由Pan等[15-16]提出的一种基于特征的迁移学习方法，通过将训练样本和测试样本映射到低维潜在空间寻找公共迁移成分进行学习，进而减小了两样本的数据分布差异性，可以明显提高跨领域、跨任务的学习能力。其基本原理如下：

假设原始空间为Х，训练样本为DS={(xS1,yS1),...,(xSn1,ySn1)},满足边际概率分布P(XS)，其中输入xSi∈Х，输出标签为ySi∈Y；测试样本为DT={(xT1,yT1),...,(xTn1,yTn1)},满足边际概率分布P(XT)，且输入xTi∈Х，但输出标签未知。一般迁移学习方法，通常假设P≠Q且P(YS|XS)=Q(YS|XS)。但实际应用中，由于噪声和观测数据的动态变化，条件概率分布P(Y|X)会因此发生变化。本文假设P≠Q，且存在函数Ф能够满足P(Ф(XS))≈P(Ф(XT))与P(YS|Ф(XS))≈P(YT|Ф(XT))。

假设Ф是普通核函数映射，分别满足分布P和Q的训练样本与测试样本之间的距离表达式描述为

(1)

依据核函数优势，可以将两个样本数据之间的距离表示为

(2)

其中，K=[Ф(xi)TФ(xj)]；

TCA算法通过统一核函数将两个样本集的特征映射到同一个核空间。首先在潜在空间(核空间)上投影，上述核矩阵K可以

K=(KK-1/2)(K-1/2K)

(3)

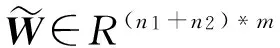
(4)

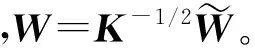
(5)

由式(5)得潜在空间的嵌入数据是WTK，其中第i列嵌入坐标Xi由[WTK]i提供。因此投影样本方差为WTKHKW，中心矩阵H=In1+n2-1/(n1+n2)*11T,1∈Rn1+n2是全为1的列向量，In1+n2∈R(n1+n2)*(n1+n2)是单位矩阵。

综上所述，需要解决的最优化问题见式(6)

minW=tr(WTKLKW)+μtr(WTW)
s.t.WTKHKW=Im

(6)

式中μ>0是权衡系数，Im∈Rm+m是单位矩阵。

上述W优化问题可转化为跟踪优化问题进行求解，在此不再赘述。

另外，本文选用高斯核函数对迁移成分进行讨论，其表达式为

(7)

2 迁移成分分析仿真分析

传统的机器学习方法要求训练样本与测试样本数据满足同一分布，当两样本分布不同时，难以进行有效学习，而TCA算法可以拉近两样本分布。随机生成两组二维数据，如图2(a)所示，三角表示训练样本数据，圆形表示测试样本数据。分别利用高斯核函数下的TCA算法与主成分分析法(Principle Component Analysis, PCA)以及核主成分分析法(Kernel Principle Component Analysis, KPCA)，将二维样本数据均降维至一维，并绘制各自概率密度曲线。如图2(b)～(g)所示，经PCA和KPCA降维后的测试样本与训练样本分布之间差异依然很大，与之相比，TCA算法可以明显地减小测试样本与训练样本的分布差异，使降维后两样本数据分布几乎相同。

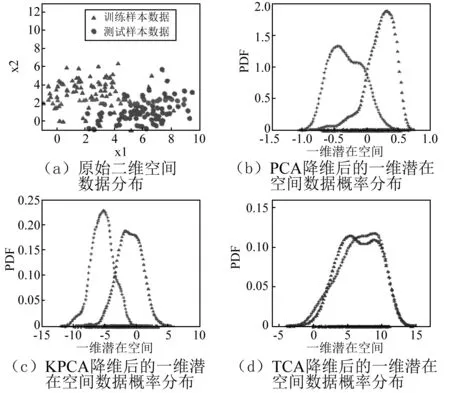
图2 各算法性能比较Fig. 2. Comparison of different algorithms

3 基于不同工况下辅助数据集的齿轮箱故障诊断实验分析

3.1 基于不同工况下辅助数据集与TCA的故障诊断方法

基于迁移成分分析的齿轮箱故障诊断方法如图3所示，大致分为实验台搭建、数据采集、特征提取、特征选择、模式识别等步骤。这里，训练样本和测试样本为不同工况下的数据集，对比讨论训练数据中两种工况数据占用不同比例时不同方法的性能，在特征选择中，应用TCA算法与传统机器学习算法进行对比分析。

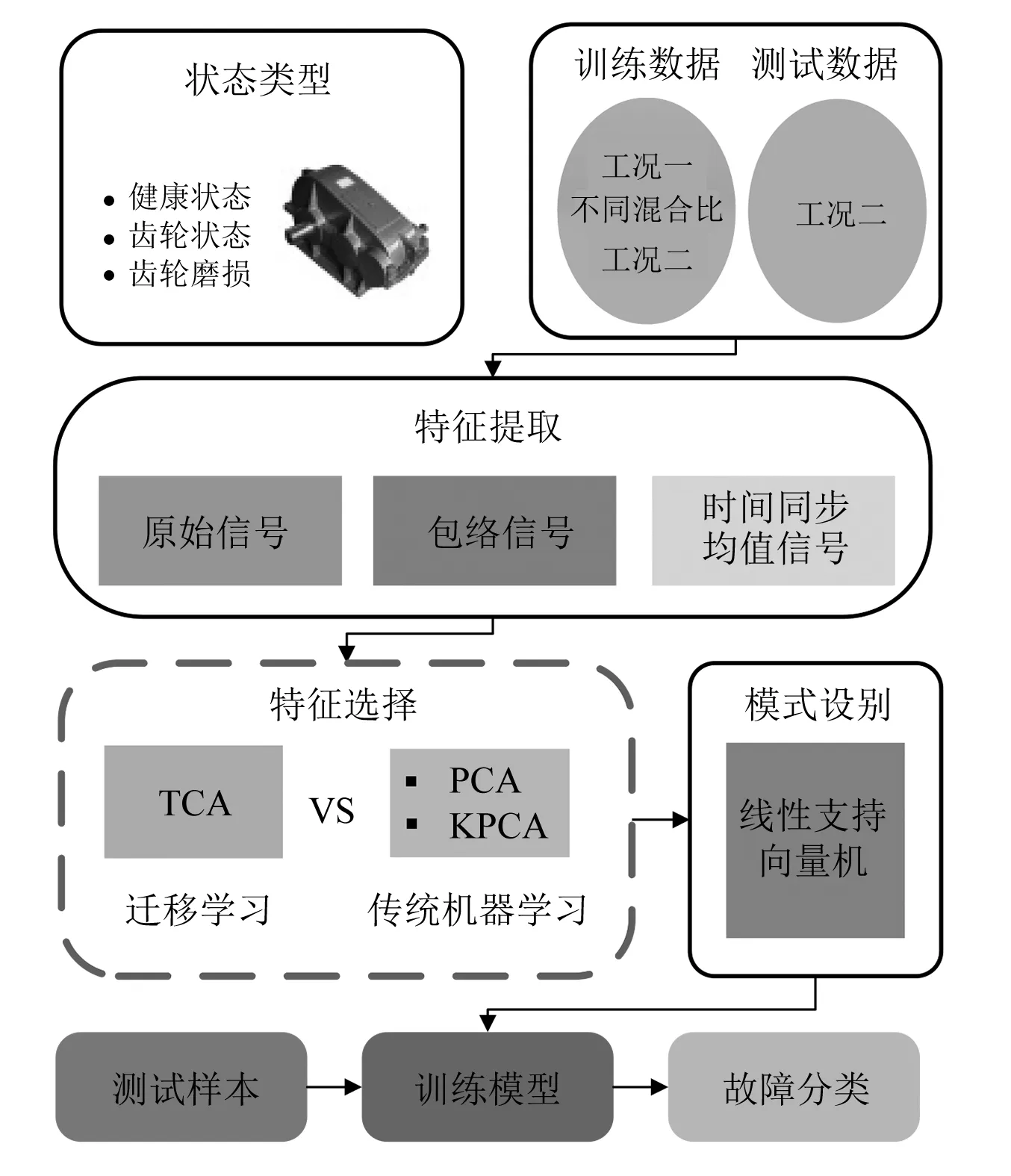
图3 齿轮箱故障诊断流程Fig. 3. Framework for gearbox fault diagnose

3.2 齿轮箱故障模拟实验

齿轮箱故障模拟实验系统由二级齿轮箱、电机、传感器等数据采集系统组成，实验台总图、齿轮箱内部结构以及传感器布置情况如图4所示。其中，对齿轮箱输入端与输出端均布置加速计和转速计，其采样频率均为66 666.67 Hz。

图4 齿轮箱实验台总图[17]Fig.4 Overview of the gearbox apparatus[17]

本次齿轮箱模拟故障形式为齿面剥蚀和齿轮断裂，与正常齿轮的对比如图5所示，(a)～(c)依次为正常、齿面剥蚀和齿轮断裂实物图及对应的时域波形图。

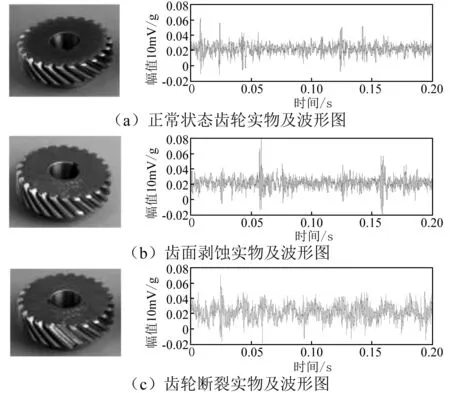
图5 齿轮正常、齿面剥蚀和齿轮断裂实物及波形对比图Fig.5 Comparison of photo and waveform of normal gear, chipped gear and broken gear.

3.3 齿轮箱信号特征提取

通过加速计和转速计采集到的信号信噪比较大，导致采集到的原始信号和齿轮箱故障信号可能存在较大差别。因此，合理的特征提取是提高故障诊断准确率的保证。这里对齿轮箱输入端原始加速度信号进行包络谱分析以及时间同步均值分析，绘制齿轮正常和两种故障模式时的加速度信号时域包络波形图如图6～8所示。

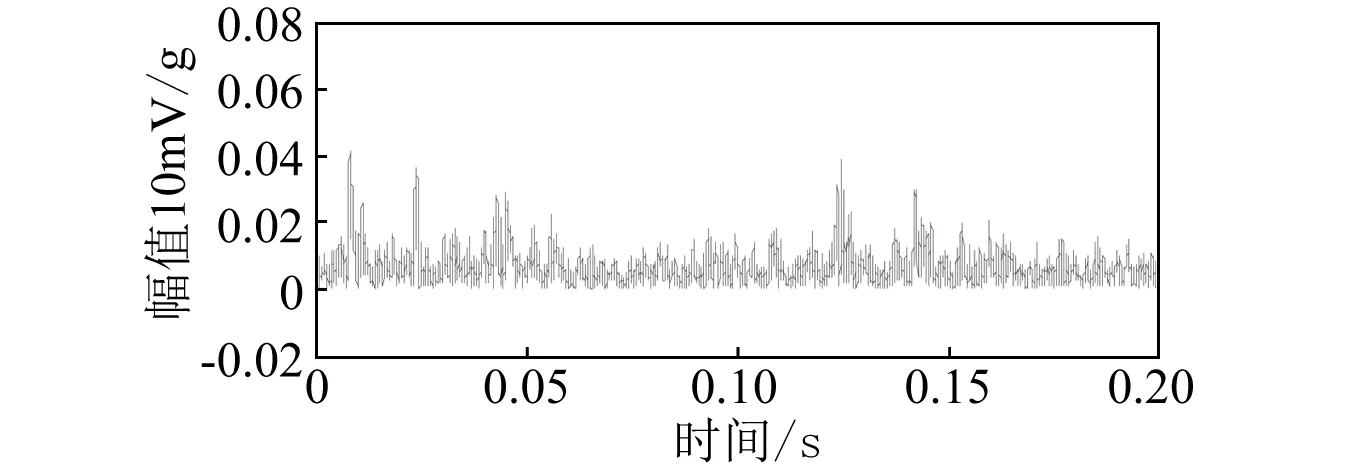
图6 正常状态时域包络波形图Fig.6 Time-domain envelope waveform of normal gear

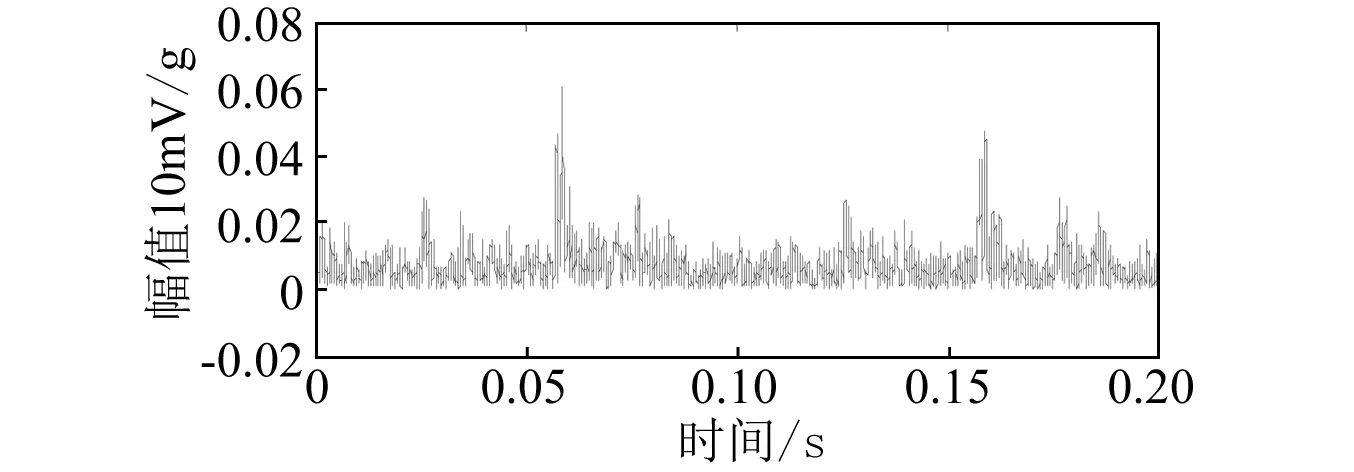
图7 齿面剥蚀时域包络波形图Fig.7 Time-domain envelope waveform of chipped gear

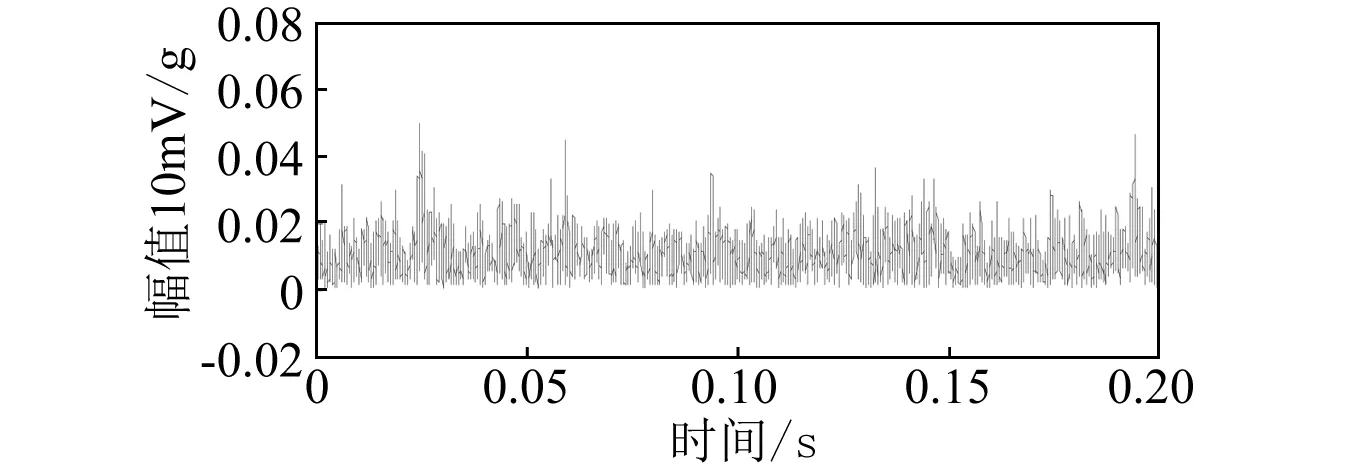
图8 齿轮断裂时域包络波形图Fig.8 Time-domain envelope waveform of broken gear

分别对原始信号、包络信号以及时间同步均值信号选择均方根、峭度值、峰峰值、峰值因子、能量因子等公共特征，由于时间同步均值方法作为齿轮箱信号分析方法可以避免转速带来的差异性[18]，因此对时间同步均值信号额外进行特征提取[19]，如表1所示。

表1 齿轮箱信号特征指标

3.4 基于不同工况下辅助数据集与TCA的齿轮箱故障诊断

将选择的特征通过TCA进行学习，然后通过线性支持向量机(Support Vector Machine, SVM)分类，其中，μ赋值0.1，m分别取值5, 10, 15, 20, 25。利用单一工况齿轮箱三种状态(正常、齿面剥蚀、齿轮断裂)下的数据和另一工况(不同转速、不同载荷)下齿轮箱三种状态(正常、齿面剥蚀、齿轮断裂)的数据在0～100%范围内，跨度为10%的不同百分比数据作为训练数据训练支持向量机模型，将另一工况(不同转速、不同载荷)下齿轮箱三种状态(正常、齿面剥蚀、齿轮断裂)的数据作为测试数据，利用训练好的模型对其进行故障分类，通过正确的分类组数除以测试数据组数得到故障诊断准确率。其中，每组测试数据均为40组数据，实验次数为5，计算诊断准确率平均值即为最终故障诊断准确率。本文齿轮箱跨工况类型主要为不同转速，不同负载，相同转速，不同负载以及不同转速相同负载下一种工况到另一种工况的学习，计算故障诊断准确率。计算结果如图9、10和表2所示，以30H为例说明工况数据集含义：其中30表示，转速操作频率为30 Hz，H/L表示高负载(high load)或低负载(low load)，因此30H表示齿轮箱处在30 Hz高负载工况下；No_Sel表示未使用特征选择算法，直接进行SVM分类；原始数据比例表示训练数据中训练工况数据所占的比例， 0表示用同一种工况下的数据做训练和测试，10%表示训练工况数据占训练数据10%，测试工况数据占90%，测试数据全部为另一种工况下的数据；100%表示用一种工况下的数据做训练，另一种工况下的数据做测试。

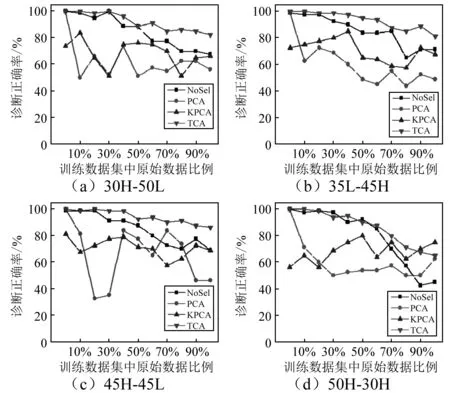
图9 不同原始数据比例下几种算法诊断准确率比较Fig. 9 Comparison of diagnostic accuracy of several algorithms under different raw data proportions

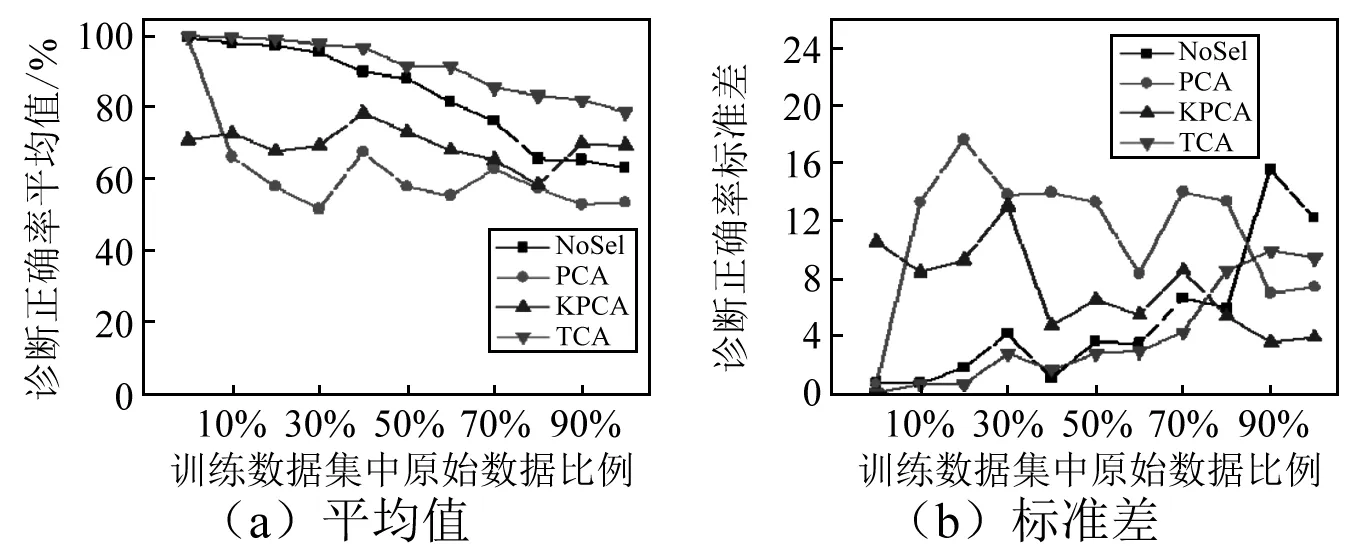
图10 不同原始数据比例下几种算法诊断准确率平均值和标准差比较Fig.10 Comparison of the mean value and standard deviation of the diagnostic accuracy of several algorithms under different raw data proportions

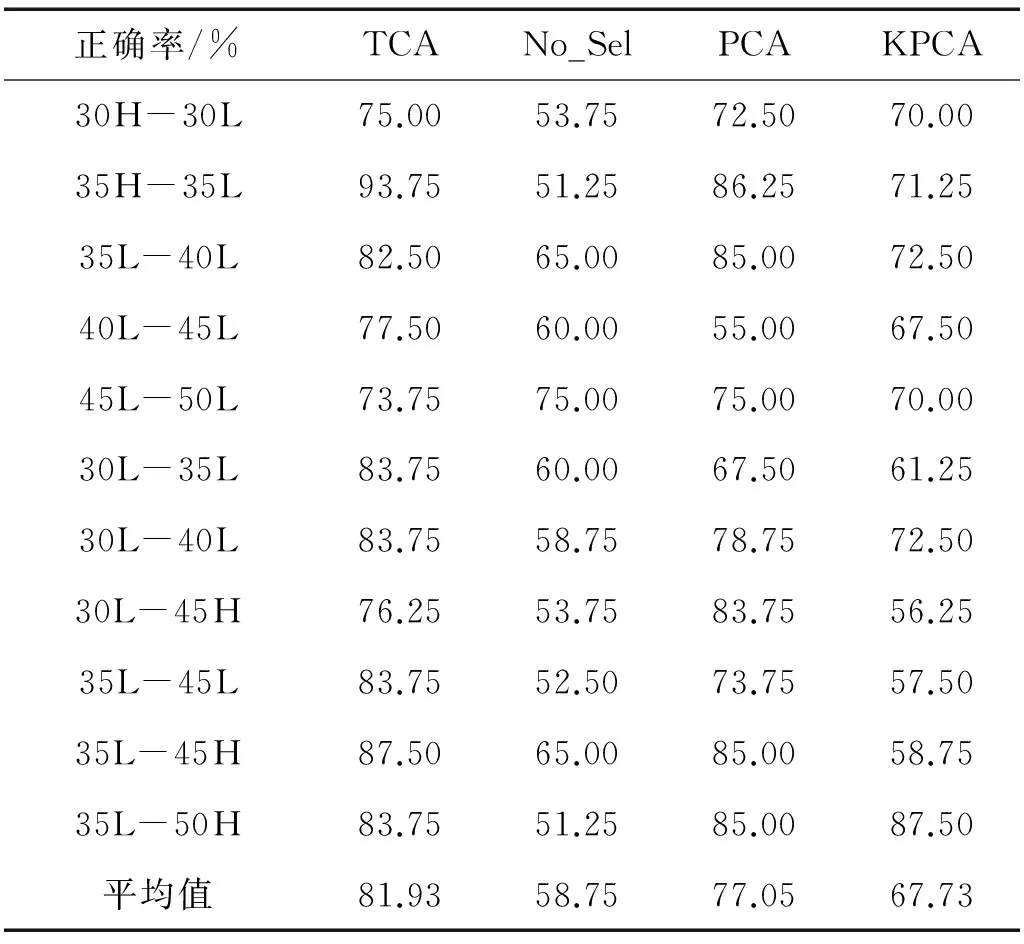
表2 TCA算法和其他算法诊断准确率对比

3.5 TCA与传统特征选择方法的分析比较

由图9和图10可知，不同工况条件下经TCA特征选择后的迁移诊断模型诊断准确率普遍高于经PCA与KPCA传统特征选择处理后的诊断模型，同时也高于未使用特征选择算法的诊断模型。两种工况下，四种方法得到的分类准确率随着原始数据在训练数据中所占比例的增加而降低，其中TCA算法在各原始数据比例下都有较高的优势，平均诊断准确率高于其余三种方法，TCA在训练数据集中原始数据比例较低的时候达到最高诊断准确率，在比例较高时依然有很高的诊断准确率，性能最优。

在没有原始工况辅助数据下，对比TCA算法和其他特征选择方法对齿轮箱故障分类效果，分类器仍为线性SVM。由表2对比四种算法在两种工况下的分类准确率平均值可知，PCA与KPCA算法诊断准确率高于未使用任何特征选择算法下的诊断准确率，同时明显低于TCA诊断准确率5～18个百分点。因此TCA诊断模型可以较好的实现对齿轮箱故障的正确分类，大大提高了变工况齿轮箱故障诊断的正确率和可靠性。

4 结 论

本文提出基于不同工况下辅助数据集的迁移成分分析算法用于齿轮箱故障诊断，研究变工况下齿轮箱迁移诊断机制。通过仿真分析和实验验证，得到以下结论：

(1) TCA算法作为一种跨领域、跨任务的学习方法，通过将训练样本和测试样本映射到低维潜在空间，寻找公共迁移成分进行学习，进而减小了两样本的数据分布差异性，从原理上突破了训练样本和测试样本必须满足数据同分布的限制，在理论上为齿轮箱故障的迁移诊断提供了可能。

(2) TCA算法诊断准确率随着原始数据在训练数据集中所占比例的增加而降低，始终维持在较高水平，在原始数据所占比例较低时性能最优，特别是在所占比例较高时依旧有很高的准确率，可以明显提高齿轮箱在变工况下的故障诊断准确率和可靠性。

(3) 在没有原始工况辅助数据下，与传统机器学习算法相比，迁移成分分析算法平均诊断准确率明显高于其他方法。故障诊断准确率平均提高了5～18个百分点。

[1] 邹今春, 沈玉娣．变工况齿轮箱故障诊断方法综述[J]．机械传动, 2012, 36(8):124-132. ZOU Jinchun, SHEN Yudi. A review of gearbox fault diagnosis methods in variable working conditions [J]. Journal of Mechanical, 2012, 36(8):124-132.

[2] 徐刚, 骆志高, 李明义, 等.变工况运行的机械故障诊断研究[J].机械工程学报, 2001, 37(12):104-107. XU Gang, LUO Zhigao, LI Mingyi, et al. Mechanical fault diagnosis research in variable working conditions[J]. Journal of Mechanical Engineering, 2001, 37(12):104-107.

[3] 程利军，张英堂，李志宁，等．基于时频分析及阶比跟踪的曲轴轴承故障诊断研究[J]．振动与冲击，2012，31(19) :73-78． CHENG Lijun，ZHANG Yingtang，LI Zhining, et al．Fault diagnose of an engine’s main bearing based on time-frequency analysis and order tracing[J]. Journal of Vibration and Shock，2012，31( 19) : 73-78．

[4] 孙自强，陈长征，谷艳玲，等．基于混沌和取样积分技术的大型风电增速箱早期故障诊断[J]．振动与冲击，2013，32(9) : 113- 117． SUN Ziqiang，CHEN Changzheng，GU Yanling et al．Incipient fault diagnosis of large scale wind turbine gearbox based on chaos theory and sampling integral technology[J]．Journal of Vibration and Shock，2013，32(9): 113-117．

[5] 李友荣，曾法力，吕勇，等．小波包分析在齿轮故障诊断中的应用[J]．振动与冲击，2005，24 (5) : 101-103． LI Yourong，ZENG Fali，LÜ Yong，et al．Gear fault diagnosis by using wavelet packet[J]．Journal of Vibration and Shock，2005，24( 5) : 101 - 103．

[6] PAN S J, YANG Q . A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10):1345-1359.

[7] LU J, BEHBOOD V, HAO P, et al. Transfer learning using computational intelligence[J]. Knowledge-based Systems, 2015, 80:14-23.

[8] PEREIRA J C, VASCONCELOS N. Cross-modal domain adaptation for text-based regularization of image semantics in image retrieval systems[J]. Computer Vision and Image Understanding, 2014, 124:123-135.

[9] PATEL V M, GOPALAN R, LI R, et al. Visual domain adaptation: a survey of recent advances[J]. IEEE Signal Processing Magazine, 2015, 32(3):53-69.

[10] REN C X, DAI D Q, HUANG K K, et al. Transfer learning of structured representation for face recognition[J]. IEEE Transactions on Image Processing, 2014, 23(12):5440-5454.

[11] DENG J, ZHANG Z, EYBEN F, et al. Autoencoder-based unsupervised domain adaptation for speech emotion recognition[J]. IEEE Signal Processing Letters, 2014, 21(9):1068-1072.

[12] ZHANG L, ZHANG D. Domain adaptation extreme learning machines for drift compensation in E-Nose systems[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(7): 1790-1801.

[13] 周书恒，杜文莉. 基于迁移学习的裂解炉产率建模[J]. 化工学报，2014, 65(12):492-498. ZHOU Shuheng, DU Wenli. Modeling of ethylene cracking furnace yields based on transfer learning[J]. CIESC Journal, 2014, 65(12):492-498.

[14] HUANG S, LI J, CHEN K, et al. A transfer learning approach for network modeling[J]. IIE Transactions, 2012, 44:915-931.

[15] PAN S J, KWOK J T, YANG Q. Transfer learning via dimensionality reduction[C]∥Proc 23rd AAAI Conf Artif Intell. Chicago, IL, 2008: 677-682.

[16] PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. Neural Networks, IEEE Transactions on, 2011, 22(2): 199-210.

[17] PHM SOCIETY.PHM Data Challenge[DB/OL].https://www.phmsociety.org/competition/PHM/09/#userconsent#, 2009.

[18] 罗德扬. 时域同步平均原理与应用[J].振动、测试与诊断, 1999, 19(3): 202-207. LUO Deyang. Time domain synchronization average principle and application[J]. Journal of Vibration, Measurement & Diagnosis, 1999, 19(3): 202-207.

Gearbox diagnosis based on auxiliary monitoring datasets of different working conditions

DUAN Lixiang，XIE Junyao，WANG Kai，WANG Jinjiang

(School of Mechanical and Transportation Engineering, China University of Petroleum, Beijing 102249, China)

In view of the low reusability of monitoring data, the influence of complex working conditions and the usual failure of trained model, the transfer component analysis (TCA) was introduced for the equipment fault diagnosis in variable working conditions based on auxiliary monitoring data of different working conditions. The TCA method decreases the distribution difference between training sample and test sample, by utilizing a kernel function to map the feature of the two samples to a latent space. Besides, the effect of different proportion of monitoring data under various working condition was compared and analyzed in TCA algorithm performance. According to the simulation analysis and experiment verification, compared with traditional machine learning methods, the TCA performs better in the reduction of distribution difference between the two kinds of samples and improves reusability of monitoring data under different operational conditions and gearbox diagnosis accuracy and reliability.

gearbox; different working condition; auxiliary dataset; fault diagnosis; transfer component analysis (TCA)

国家自然科学基金(51504274；51674277)；国家重点研发计划(2016YFC0802103)；中国石油大学(北京)自然科学基金(2462014YJRC039；2462015YQ0403)

2015-12-22 修改稿收到日期： 2016-03-24

段礼祥 男，博士，副教授，1969年生

王金江 男，博士，副教授，1981年生

TH132.41

A

10.13465/j.cnki.jvs.2017.10.017