基于高阶矩阵函数的广义逆波束形成改进算法

陈 思，张志飞 1，，徐中明 1，，贺岩松 1，，黎 术

(1.重庆大学 机械传动国家重点实验室，重庆 400030； 2.重庆大学 汽车工程学院，重庆 400030)

基于高阶矩阵函数的广义逆波束形成改进算法

陈 思2，张志飞1，2，徐中明1，2，贺岩松1，2，黎 术2

(1.重庆大学 机械传动国家重点实验室，重庆 400030； 2.重庆大学 汽车工程学院，重庆 400030)

广义逆波束形成是一种高效的声源识别定位方法，然而其计算稳健性易受随机噪声影响，阻碍了其声源识别动力学水平进一步提高。为改善广义逆波束形成声源识别方法的稳健性，基于高阶矩阵函数提出一种广义逆波束形成改进算法：定义了基于广义逆波束形成的正则化矩阵；对正则化矩阵与波束形成输出进行迭代运算；利用高阶矩阵函数对迭代求解所得广义逆波束形成输出的互谱进行优化。通过数值仿真详细分析了声源频率对波束形成矩阵函数阶次取值的影响，得到阶次的最优取值区间。最后通过数值模型和实验算例对单极子与相干声源进行定位识别，结果表明:改进算法在准确识别声源基础上能有效抑制旁瓣干扰，且具有更高的声源识别精度。

传声器阵列；声源识别；广义逆波束形成；高阶矩阵函数

基于传声器声阵列测量的波束形成是一种高效的声源识别定位方法。目前已发展出多种波束形成[1,2]算法,包括传统波束形成、自适应波束形成[3]、反卷积[4-5]和广义逆波束形成[6-8]。传统波束形成空间分辨率较低，自适应波束形成无法准确识别声源强度，因此两者应用范围受限。反卷积波束形成虽不存在以上问题，但计算效率很低。广义逆波束形成能通过较少求逆迭代过程有效降低旁瓣级水平、提高声源识别精度，近年来得到广泛运用。然而其迭代求逆过程易受到干扰随机噪声和测量误差影响，需要通过适当的正则化方法[9-11]消除原求解过程存在的不适定性。

Nelson等[12]通过奇异值分解方法对广义逆波束形成传递矩阵的条件数进行研究，并将Tikhonov正则化方法应用于广义逆波束形成； Suzuki[13]在L1范数广义逆波束形成中引入正则化因子经验公式。以上研究结果表明，正则化方法可有效提高广义逆波束形成的声源识别精度和稳健性。实际应用中，传统广义逆波束形成算法很难适应复杂的声学测试环境，仅通过选择正则化参数[14-15]无法保证原算法具有足够的稳健性与识别精度。Padois等[16-17]将重新定义的正则化矩阵应用于波束形成反问题的求解，并以风洞实验加以验证，取得了较好的声源识别效果，表明选择一定形式的正则化矩阵对提升广义逆波束形成算法稳健性是必要的。

Dougherty[18-19]针对传统波束形成提出一种基于高阶矩阵函数的新算法，该方法将高阶矩阵函数与传统互谱波束形成结合，在保证较高计算效率同时大幅提升了声源识别精度。为了进一步提高广义逆波束形成性能，将高阶矩阵函数方法引入广义逆波束形成中，并对正则化矩阵与波束形成输出进行迭代优化，提出了一种广义逆波束形成改进算法。通过数值仿真分析了声源频率和信噪比等因素对阶次选择的影响，得到阶次取值的最优区间；分别以单极子和相干声源为研究对象，通过对比仿真和试验验证了广义逆波束形成改进算法的正确性与实用性。

1 广义逆波束形成原理

传统波束形成根据传声器阵列的各个传声器接收的声音信号的时间差以及传声器的位置来确定声源的方位。其目的为对传声器阵列中各阵元的输出进行延时、加权、求和等运算，以补偿各阵元上的传播延时，将输出信号聚焦到指定声源方位，在声源方向上得到了空间响应的极大值，从而实现声源识别[18-19]。传统波束形成的基本算法如下式所示：

q=Wp

(1)

式中：q为声源所在扫描平面上的N维声压强度向量，即所求波束形成输出结果；p为传声器阵列测得的M维声压强度声向量；W则为包含了由传声器阵列各点到声源扫描平面各点方向信息的N*M维导向矩阵。

与传统波束形成不同，广义逆波束形成以单极子声源为假设得到声源平面到传声器阵列的声学响应传递方程式(2)，该方程的建立基于数学物理反问题思想，可准确描述声场空间信息。

p=Gq

(2)

式中，G为M*N维声学传递函数，其中声学传递函数表征的是声源到传声器阵列的理论声波辐射模型。显然通过求解式(2)即可得到声压强度向量q，然后利用声压强度向量即可重构声源平面声源分布。然而大多数情况下，声学响应传递方程是具有不适定性的，无法通过直接对传递矩阵求逆得出满意的声源面成像结果。为此，需要采用结合了正则化方法的广义逆方法在消除这种不适定性的同时近似求解方程式(2)。该方法首先将声学响应传递方程转化为如下加权的Tikhonov最小化问题：

(3)

式中，L-1为正则化方阵，其取值将在后文3.1节中详细讨论。然后通过广义逆方法迭代求解式(3)，即可以得到实际声压强度向量。

qn+1=L(n)HH(HHH+λIM)-1p

(4)

式中，矩阵H=GL(n)=[h1,…,hs,…,hN]H，其中[·]H为矩阵的共轭转置，[·](n)表征着第n步迭代值。λ为Tikhonov正则化因子，其值参考文献[6]中的经验取值，即为方阵HHH的最大特征值的1%～10%。最终通过求解得到的声压强度向量重构出实际声源平面的声源分布，利用声源分布即可识别主要噪声源方位与声源强度，从而为噪声控制提供可靠依据。

2 广义逆波束形成改进算法

广义逆波束形成由于运用广义逆技术进行迭代求解，使得其相对于传统波束形成具有更高的空间分辨率，能够准确高效地进行声源识别。然而由于其迭代的计算时效与本身动力学性能的限制，对于一些复杂的声源不能准确识别且易受背景噪声干扰的影响。为提高广义逆波束形成的动力学性能，增强声源重构的精度与动态性能，本文参考高阶矩阵函数波束形成方法结合正则化矩阵定义提出一种改进的广义逆波束形成方法。

2.1 基于正则化矩阵的改进

第1节给出了波束形成声学响应传递方程的Tikhonov正则化解表达式。基于经典Tikhonov正则化方法的传统广义逆波束形成，其求解过程仅使用正则化参数λ消除传递方程的不适定性而令正则化矩阵L为单位阵，由于正则化参数无法充分反映实际声源分布，故不能得到满意的正则化效果，从而无法准确识别定位声源。

本文在将高阶矩阵函数与广义逆波束形成结合的基础上，通过在迭代加权过程中引入基于波束形成的正则化矩阵L，对声源识别结果进行加权优化，使得声源识别结果更加精确。所引入的基于广义逆波束形成的正则化矩阵如式(5)所示：

(5)

为便于后续分析与算法改进，首先对声源平面任意聚焦点的波束形成输出声源强度进行归一化处理：定义加权导向向量A(n)=L(n)B，其中B为归一化矩阵，取值为B=[B1,...,BS,...,BN]H，其分量取值如下式所示：

(6)

式中，矩阵α=(HHH+λIM)-1对于声源识别输出结果影响较大，其取值受限于正则化参数λ和矩阵H。其中正则化参数可通过经典的L曲线和广义交叉验证等数值方法来进行精确选取。

式(4)所示波束形成输出进行归一化后可简化为如下形式：

qn+1=L(n)Bp=A(n)p

(7)

对比式(7)与式(1)易见，广义逆波束形成的输出结果与传统波束形成在表达形式上具有一致性，不妨令We=A(n)为等效的导向矩阵。

该优化的正则矩阵中向量元素通过离散平滑范数和无穷范数在保证波束形成输出整体不变的基础上对声源识别结果进行了归一化，使得声压强度向量中具有较高声能量的声源分量在迭代过程中逐渐收敛于实际声源分布，而相对声源分量而言能量较低的非声源分量部分则被抑制而逐渐衰减。基于波束形成问题定义的正则化矩阵不仅加快了算法迭代收敛速度，而且减弱了波束形成输出对正则化参数的依赖，增强了算法稳健性。

2.2 基于高阶矩阵函数的改进

取式(7)所示q(n+1)的互谱得到如下广义逆波束形成的互谱形式：

(8)

式中，C=ppH为声压向量的互谱。由于C是正定矩阵和Hermitian矩阵，可对其进行如下特征分解：

C=UΣUH

(9)

式中，U为特征向量矩阵，Σ为对角特征值矩阵。

首先参考高阶矩阵函数波束形成定义一个基于互谱矩阵的矩阵函数f(C)，如式(10)所示:

f(C)=Udiag(f(δ1),...,f(δM))UH

(10)

式中，δM是Σ的第M个特征值。当矩阵函数f=t1/v时，可以得到互谱矩阵的指数形式：

(11)

将上式中互谱矩阵的指数形式替换广义逆波束形成互谱表达式中互谱矩阵，并将其波束输出结果取v次方后得到如下v阶矩阵函数表达式：

(12)

提取式(12)中波束形成输出Qv的对角元素，开方即得改进后的基于高阶矩阵函数的广义逆波束形成输出。算法流程图如图1所示。

通过对声压互谱进行特征分解可以滤除较小特征值对应的噪声成分。而采用高阶矩阵函数方法对式(8)进行优化可以进一步突出主要声源信息，使波束形成输出以阶次形式急剧收敛于真实值，从而在准确识别声源的基础上有效提高广义逆波束形成的动态性能。

需指出的是，在互谱矩阵的指数形式求解过程中，一般采用阈值截断滤波来滤除较小特征值，以降低干扰噪声的影响。而选择合适的阈值至关重要，较小的阈值将导致降噪不彻底；阈值过大则有可能导致声源面重要信息丢失，从而使得重建之后的声源识别结果与真实值具有较大偏差。理想阈值应保证声源信息能够精确重建，在本广义逆波束形成改进算法中建议将截断阈值取为最大特征值的1%～5%左右即可。

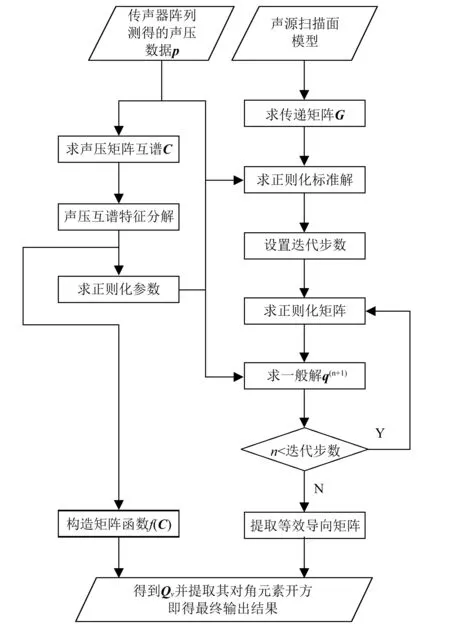
图1 改进算法流程图Fig.1 Flow diagram of modified algorithm

2.3 最优阶次的选取

对于改进后的广义逆波束形成算法，阶次v的选择至关重要。理论上来说阶次v的取值易受测量误差和声源频率等因素的影响，例如由于测量误差的存在导致理论与实际导向向量之间相位不匹配，当阶次v选择不适当时，将导致测量误差无限放大进而造成错误的声源识别定位结果。下面通过数值仿真求解阶次v的最优取值范围。

首先定义一个关于广义逆波束形成性能的函数RES，该函数与声源识别的空间分辨率相关。函数值越小，声源识别精度越高。为简化数据分析，假设真实声源分布于声源平面中心，利用36通道矩形传声器阵列在离声源平面0.5 m处进行声压数据测量。最后将广义逆波束形成算法计算得到的波束形成输出与其最大响应值做比值，然后通过对数函数进行归一化处理。

RES=

(13)

式中，RES亦可表示为声源中心“半径”，其中bmax为波束输出响应峰值点处对应半径，b-15 dB为对应-15 dB点处的声学中心半径，<*>为空间数据的几何平均值。声源中心“半径”RES同时也从侧面反映了波束响应的主瓣张角的大小， RES数值越小，声源能量越集中，声源识别定位越准确，从而表明RES能够充分反映广义逆波束形成声源识别的性能。通过数值仿真绘制出不同声源频率下RES随阶次变化的关系曲线，如图2所示。

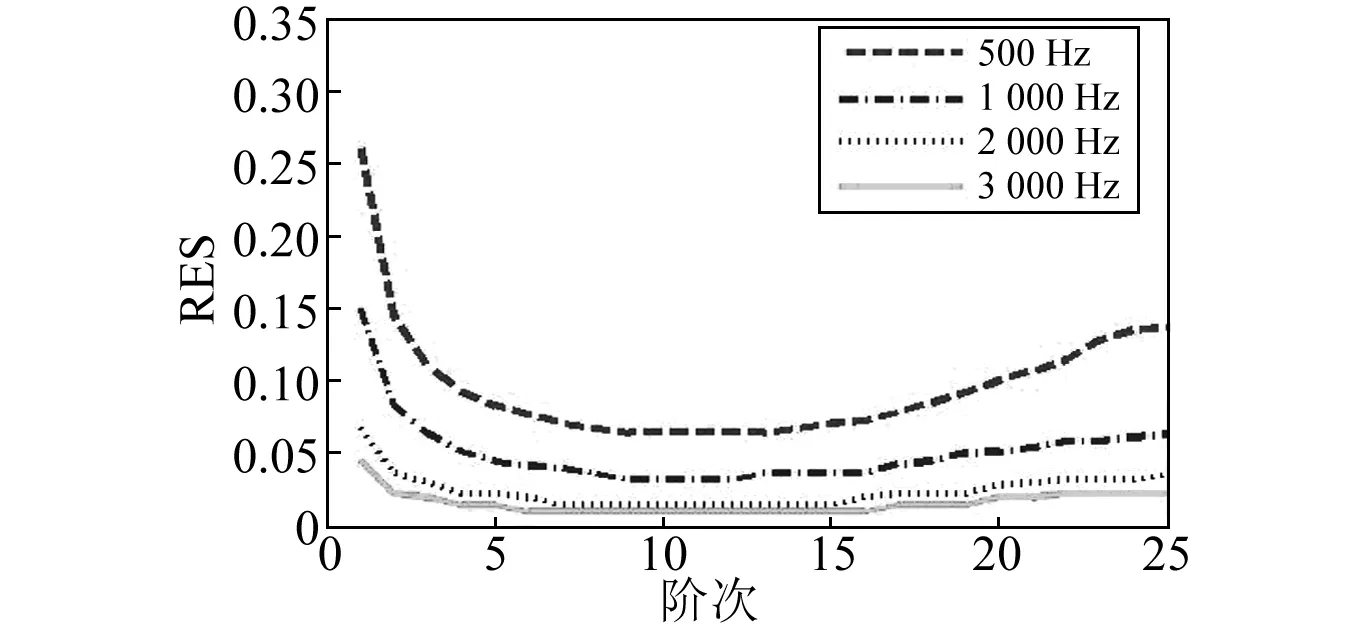
图2 不同声源频率下RES随阶次变化曲线(SNR:15 dB)Fig.2 The simulation result of RES at different frequencies

由图2的数值仿真结果可知，声源频率越高声源中心“半径”RES越小，表示主瓣宽度越低，即声源识别精度更高。在不同声源频率下，随着阶次数增加，声源中心“半径”逐渐减小，识别精度提高；然而当阶次高于某一门限值，继续增加阶次值，RES数值反而随之增加。此时由于阶次取值过大，测量误差被急剧放大，进而降低了声源识别的空间分辨率。极端情况下可能在非声源位置出现“旁瓣鬼影”，严重影响实际应用中对声源方位的判断。

以上数值仿真分析表明，改进算法在选择阶次时要考虑声源频率的影响，在合理范围内采用更高阶次值，波束输出的主瓣张角将趋于减小，声源定位精度将得到提高。根据图2所示不同代表声源频率下阶次与RES的关系，给出最优阶次的建议值为5～15。

3 算法对比研究

3.1 仿真分析

为验证改进算法的声源识别性能，利用MATLAB软件对不同波束形成方法进行对比仿真分析。对不同频率单极子与相干声源进行仿真，虚拟声源面大小为1 m×1 m，其中单极子声源位于平面中心点处，相干声源分布于(0.25,0,0)m和(-0.25,0,0)m点处。在距声源平面0.5 m处设置测量面，虚拟36通道矩形传声器阵列进行数据测量，其中传声器间距为0.1 m。为便于利用计算机进行数据后处理，将声源平面离散为41×41聚焦点的声源计算平面，数据处理过程只计算聚焦点处声源强度值。为便于不同波束形成算法之间进行声源定位性能的对比分析，将测量得到的波束输出结果利用指数函数归一化为0 dB，其动态显示范围设为-15 dB。

分别绘制式(1)所示的传统波束形成、文献[6]提出的广义逆波束形成以及广义逆波束形成改进算法在声源面上输出结果的声压强度分布图。

广义逆波束形成的迭代次数为20次，广义逆波束形成改进算法中迭代次数为5次，阶次数依次为3和10。最终运用自开发软件仿真得到的声源成像结果如图3所示。

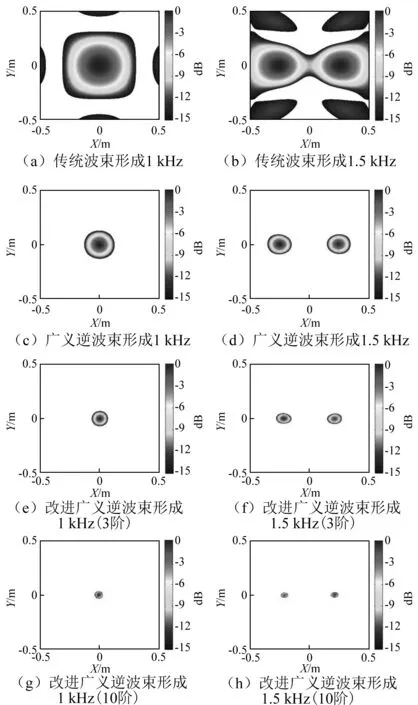
图3 声源仿真结果Fig.3 The simulation result of the sound sources

图3所示三种不同的波束形成方法声源识别成像图中，对于不同类别声源，三种声源识别算法均在目标声源方位识别出0 dB左右的声学中心，表明三者都能识别定位声源。相对于传统波束形成，广义逆波束形成类波束形成在抑制旁瓣基础上缩减了主瓣宽度，提高了声源重构精度。对于改进的广义逆波束形成算法，由图可见其声学中心覆盖范围最小。这主要是由于高阶次指数函数急剧扩大了主瓣与旁瓣之间的相对差异，掩盖了随机噪声等干扰因素，抑制了旁瓣生成，从而使得声源识别结果更加精确。此外，在一定范围内增加阶次数(如图从3阶增加至10阶),目标声源在重构声源面上产生的声学中心也将进一步缩小。而且改进的广义逆波束形成算法由于应用了基于波束形成问题的正则化矩阵，从而降低了正则化参数的影响，提高了声源识别稳健性。同时通过应用高阶矩阵函数减小了迭代循环次数，提高了算法的计算时效，这对实际工程应用意义重大。

3.2 实验验证

本实验采用B&K公司的集成了4958 型传声器的18 通道COMBO声阵列(如图4(a)所示)，并通过18通道LAN-XI数据采集前端进行数据采集。

分别以单极子和单频相干双声源为对象进行实验验证。在声阵列前方0.3 m处设置受稳态信号激励的扬声器(如图4(b)所示)。为便于进行声源成像仿真，将目标声源面重构为1 m ×1 m的声源扫描平面，并将其离散成间距为0.02 m ×0.02 m的聚焦点平面。对于单极子声源，设定其在扫描平面上的坐标为(0, 0)m；对于单频相干双声源，分别设定其坐标为(0.25, 0)m和(-0.25, 0)m。

最后，将实测数据导出，利用自开发的基于不同波束形成算法的后处理软件实现声源识别声学成像，对波束形成输出数据进行归一化处理，最终声学成像云图的动态范围为(-30, 0)dB。

图4 测试设备Fig.4 The test equipment

3.2.1 实验一

实验一分别采用文献[6]提出的广义逆波束形成与本文提出的改进算法对1 500 Hz与2 000 Hz单极子声源进行了识别，其中改进算法的阶次值设定为5。声源成像图如图5所示。

由图5可见，在代表声源频率1 500 Hz和2 000 Hz处，两种算法都能准确定位声源，原广义逆波束形成算法与改进算法都具有比原广义逆算法更高的声源识别精度以及更少的干扰旁瓣。

3.2.2 实验二

实验二仍分别采用文献[6]提出的广义逆波束形成与本文提出的改进算法对1 500 Hz与2 000 Hz相干双声源进行识别，其中改进算法的阶次值设定为5。声源成像图如图6所示。

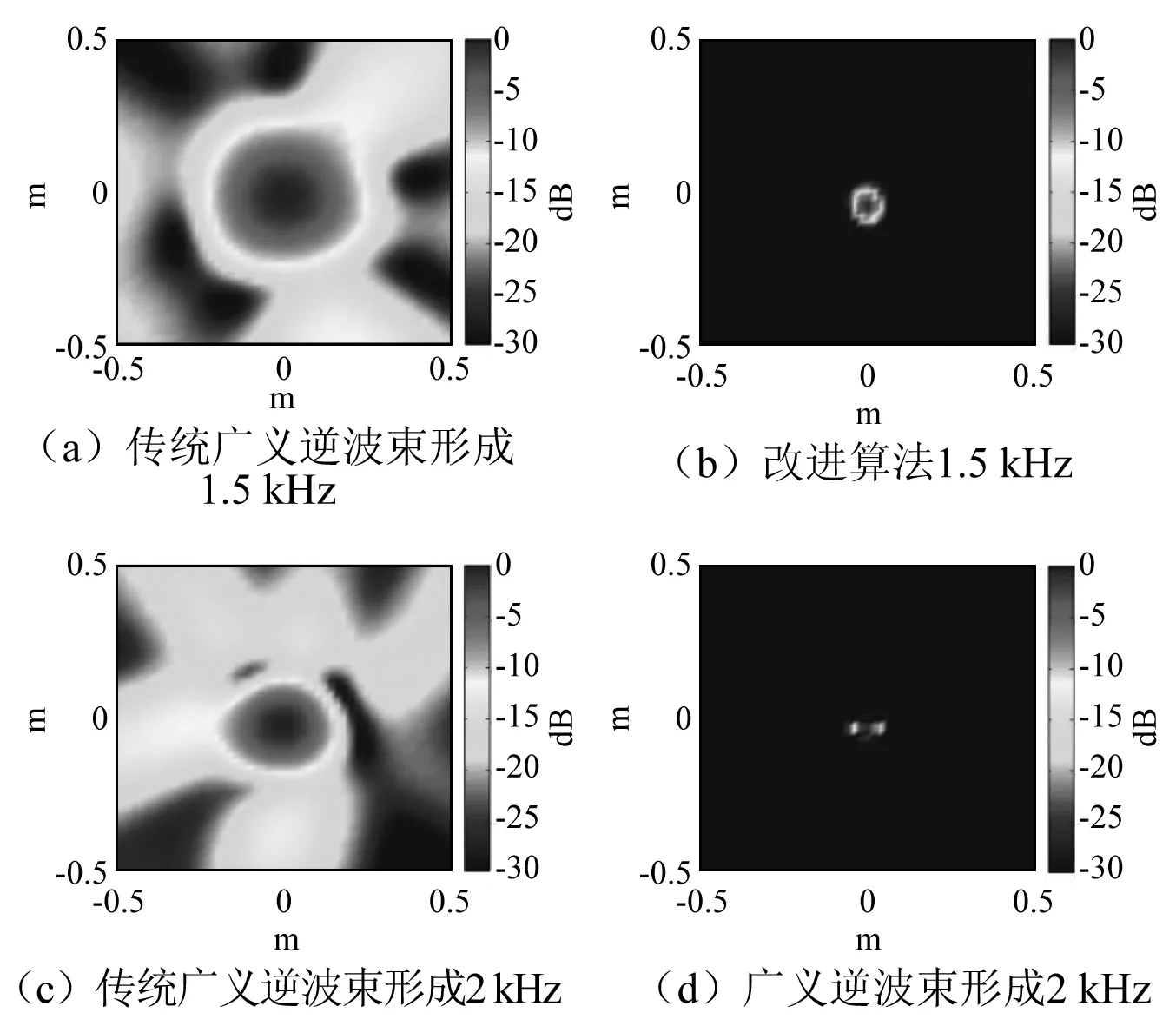
图5 单极子声源成像结果Fig.5 The monopole source beamforming outputs

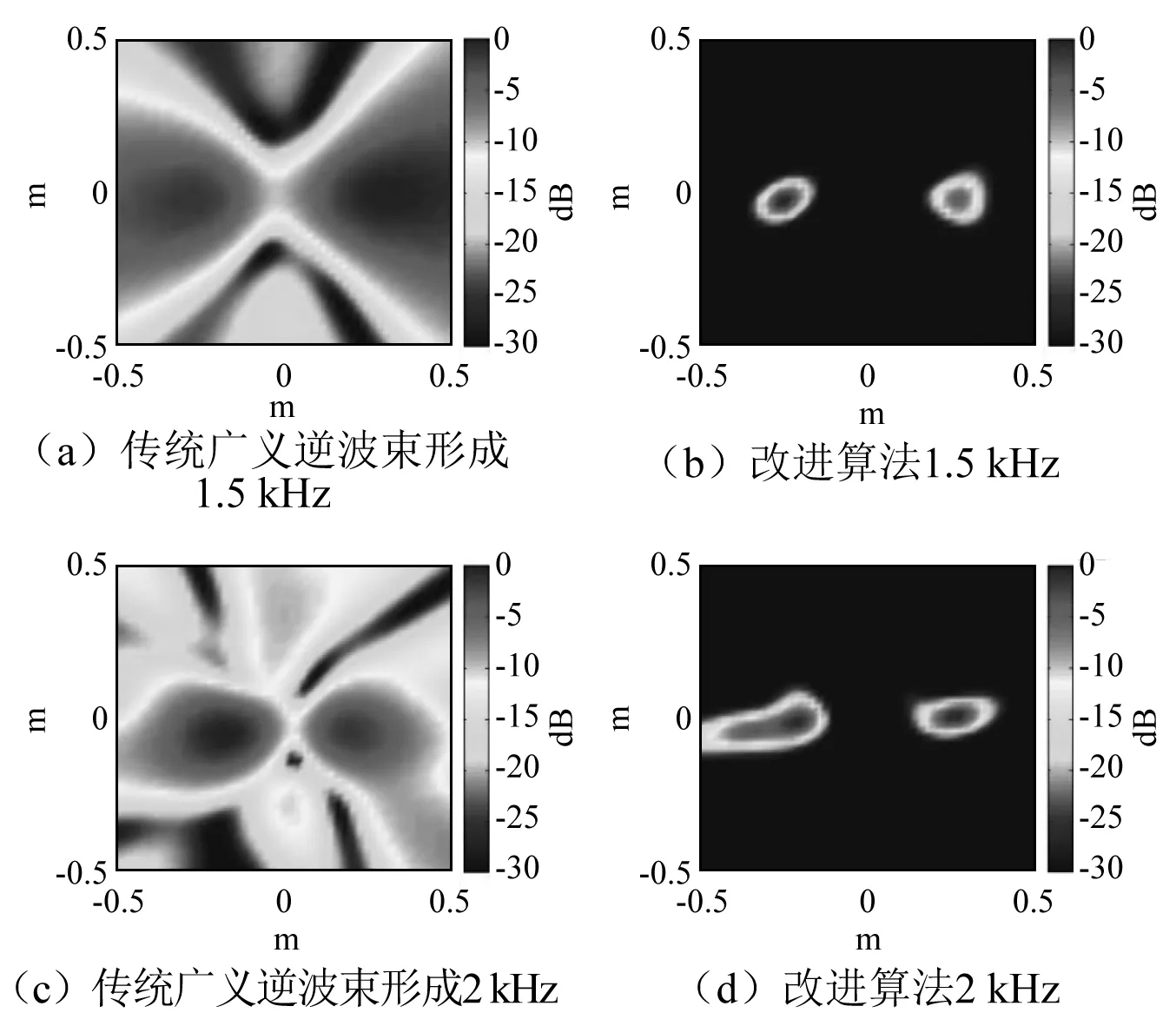
图6 相干双声源成像结果Fig.6 The coherent sources beamforming outputs

由图6可见，在1 500 Hz代表声源频率处，原广义逆算法主瓣过大，且向扫描平面两侧扩散，无法准确定位两个相干声源；改进算法在准确定位相干声源的同时，具有较高的识别精度，且对旁瓣抑制较好。而在2 000 Hz处，两种算法基本能够确定相干声源位置，考虑到图5(c)与图5(d)声学中心在扫描面上偏离实际声源的位置相对一致，原广义逆算法在声源频率提升的情况下识别效果明显改善，但改进算法仍具有更高的识别精度。

实验一与实验二的结果充分表明改进的广义逆波束形成的声源识别方法相比原广义逆波束形成方法，不仅能准确地识别定位单频单声源与相干双声源，而且能更好地抑制旁瓣产生，进而提高其声源识别的分辨率。同时试验结果也与数值仿真结果相一致，进一步验证了该方法的实用性。

4 结 论

本文在传统广义逆波束形成的基础上，充分结合高阶矩阵函数波束形成与正则化矩阵的优势，提出了一种基于高阶矩阵函数的广义逆波束形成改进算法；研究了阶次随声源频率的变化规律，得到了不同情况下最优阶次的取值区间：一般情况下最优阶次取值范围为5～15；数值仿真和实验研究表明，基于高阶矩阵函数的广义逆波束形成改进算法不仅能高效识别定位声源还能显著提高声源识别的动力学性能，与此同时亦验证了该方法的有效性。该方法在保证声源识别结果准确性的基础上进一步提高了声源识别精度。

[1] 李兵，杨殿阁，邵林，等.基于波束形成和双目视觉的行驶汽车噪声源识别[J].汽车工程, 2008, 30(10): 889- 892. LI Bing, YANG Diange, SHAO Lin, et al. Noise sources measurement and identification for moving automobiles [J]. Automotive Engineering, 2008, 30(10):889-892.

[2] CHRISTENSEN J J， HALD J. Beamforming B&K Technical Review 1[M]．2004:1-31.

[3] YONG T C，ROAN A M J. Adaptive near-field beamforming techniques for sound source imaging [J]. J Acoust Soc Am, 2009, 125(2):944-957.

[4] 杨洋，褚志刚，江洪，等.反卷积DAMAS2 波束形成声源识别研究[J].仪器仪表学报, 2013, 34(8): 1779-1786. YANG Yang, CHU Zhigang, JIANG Hong, et al. Research on DAMAS2 beamforming sound source identification[J]. Chinese Journal of Scientific Instrument, 2013, 34(8):1779-1786.

[5] BROOKS T F, HUMPHREYS W M. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays [J]. Journal of Sound and Vibration, 2006, 294(4/5): 856-879.

[6] SUZUKI T. L1 generalized inverse beamforming algorithm resolving coherent/incoherent, distributed and multipole sources [J]. Journal of Sound and Vibration, 2011, 330(24): 5835-5851.

[7] 徐中明，黎术，贺岩松，等. 光滑L0范数广义逆波束形成[J].仪器仪表学报, 2014, 35(6):1276-1281. XU Zhongming, LI Shu, HE Yansong, et al. Smoothed L0 norm generalized inverse beamforming [J]. Chinese Journal of Scientific Instrument, 2014, 35(6): 1276-1281.

[8] PENG J, HAMPTON J, DOOSTAN A. A weighted L1 minimization approach for sparse polynomial chaos expansions[J]. Journal of Computational Physics, 2014, 267(15): 92-111.

[9] EL-ATTAR R A, VIDYASAGAR M, DUTTA S R K. Algorithm for L1-norm minimization with application to nonlinear L1-approximation [J]. Society for Industrial and Applied Mathematics, 1979, 16(1):70-86.

[10] CALVETTIA D, MORIGIB S, REICHELC L, et al. Tikhonov regularization and the L-curve for large discrete ill-posed problems [J]. Journal of Computational and Applied Mathematics, 2000, 123(1): 423-446.

[11] ZOU H, HASTIE T. Regularization and variable selection via the elastic net [J]. Journal of the Royal Statistical Society Series b-Statistical Methodology, 2005, 67(2):301-320.

[12] NELSON P A, YOON S H. Estimation of acoustic source strength by inverse methods: part I, conditioning of the inverse problem [J]. Journal of Sound and Vibration ,2000, 233(4): 643-668.

[13] SUZUKI T. L1 generalized inverse beam-forming algorithm resolving coherent/incoherent, distributed and multipole sources [J]. Journal of Sound and Vibration, 2011, 330 (24): 5835-5851.

[14] 郝燕玲，成怡，孙枫，等. Tikhonov正则化向下延拓算法仿真实验研究[J]. 仪器仪表学报, 2008, 29 (3): 605- 609. HE Yanling, CHENG Yi, SUN Feng, et al. Simulation research on Tikhonov regularation algorithm in downward continuation[J]. Chinese Journal of Scientific Instrument, 2008, 29(3):605-609.

[15] 王薇，韩波，唐锦萍. 地震波形反演的稀疏约束正则化方法[J]. 地球物理学报, 2013, 56(1):289-297. WANG Wei，HAN Bo，TANG Jinping. ReguIarization method with sparsity constraints for seismic waveform inversion[J]. Chinese Journal of Geophysics, 2013, 56 (1):289-297.

[16] PADOIS T, GAUTHIER P A, BERRY A. Inverse problem with beamforming regularization matrix applied to sound source localization in closed wind-tunnel using microphone array [J]. Journal of Sound and Vibration, 2014, 333 (25): 6858-6868.

[17] GAUTHIER P A, CAMIER C, PASCO Y, et al. Beamforming regularization matrix and inverse problems applied to sound field measurement and extrapolation using microphone array[J]. Journal of Sound and Vibration, 2011, 330(24): 5852-5877.

[18] DOUGHERTY R P. Functional beamforming[C]∥ The 5th Berlin Beamforming Conference. Berlin: BeBeC,2014.

[19] DOUGHERTY R P. Functional beamforming for aero-acoustic source distributions[C]∥ The 20th AIAA Aeroacoustics Conference. Georgia, 2014.

Modified algorithm for generalized inverse beamforming based on high-order matrix function

CHEN Si2, ZHANG Zhifei1,2, XU Zhongming1,2, HE Yansong1,2, LI Shu2

(1. State Key Lab of Mechanical Transmissions, Chongqing 400030, China;2.College of Automobile Engineering, Chongqing University, Chongqing 400030, China)

Generalized inverse beamforming is an effective sound source locating method. But its calculation robustness is sensitive to random noises. For the sake of improving the robustness of generalized inverse beamforming, a modified algorithm based on high-order matrix function was proposed. The regularization matrix based on generalized inverse beamforming was defined and used in iteratively resolving the beamforming output. At the same time, the high-order matrix function was incorporated into the cross spectra of beamforming output to optimize the effect of sound source localization. Moreover, to find the optimum range of matrix function order, a numerical simulation was implemented and the influence of sound source frequency on the selection of matrix function order was analyzed correspondingly. The identifications of both monopole and coherent sound sources in some examples were realized numerically and experimentally. The results show that the proposed modified algorithm can identify the source position with higher space resolution and less side-lobe.

microphones array; sound source identification; generalized inverse beamforming; high order matrix function

国家自然科学基金(51275540)；重庆市重大应用开发计划项目(cstc2015yykfC60003)

2015-07-28 修改稿收到日期： 2016-03-17

陈思 男，硕士生，1990年6月生

张志飞 男，博士，副教授，1983年7月生

TB52

A

10.13465/j.cnki.jvs.2017.10.016