双开槽箱梁断面悬索桥的抗风性能及气动措施研究

夏锦林， 曹丰产， 葛耀君

(同济大学 土木工程防灾国家重点实验室，上海 200092)

双开槽箱梁断面悬索桥的抗风性能及气动措施研究

夏锦林， 曹丰产， 葛耀君

(同济大学 土木工程防灾国家重点实验室，上海 200092)

为研究双开槽箱梁断面桥梁的抗风性能，并提出合理的颤振和涡振气动控制措施，本文以拟建的某钢箱梁悬索桥为研究对象，开展了一系列节段模型风洞试验，并结合二维三自由度方法和CFD数值模拟分别分析了不同措施下颤振和涡振机理的改变。研究表明：相比于单箱梁断面，双开槽断面能有效的改善颤振性能；防撞栏杆基座的有无，对该类桥的颤振临界风速影响显著；中央稳定板作为改善颤振稳定性的常用手段，对提高双开槽断面颤振临界风速同样适用，且在一定范围内，临界风速与稳定板高度正相关；二维三自由度分析结果显示，中央稳定板和较优形式的栏杆均能减缓气动阻尼随风速的变化趋势。针对开槽引起涡振的问题，尝试采用各种控制措施，试验证明，均匀间隔的纵向格栅能有效的抑制涡振。结合CFD模拟，其根本原因为纵向格栅明显改变了流场绕流特性，阻碍了大规模涡脱的形成。

双开槽箱梁；颤振；气动措施；风洞试验

随着设计和施工水平的不断提高，现代桥梁的跨径也随之增大，导致结构的刚度下降，其自振频率及扭弯频率比都显著减小，使得抵抗风荷载的稳定性能成为现代桥梁设计的重要关注点，其中最为重要的就是颤振性能。颤振控制的措施一般可以分为两大类，即气动措施和机械措施。气动措施由于其有效性和经济性，在桥梁抗风设计阶段被广泛采用。对于常见的流线型箱梁断面，采用中央开槽的措施，被认为是提高颤振稳定性的可选方案之一。已建成的昂船洲大桥[1]和舟山大陆连岛工程西堠门大桥[2]都采用了箱梁中央开槽的断面形式。在Messina海峡桥方案研究中，理论分析和风洞实验结果都表明，采用中央开槽的主梁断面可得到令人满意的抗风性能[3]。

同时，交通量的日益增加要求桥梁必须具有更宽的桥面和更多的车道，常规设计都采用平行双幅桥思路，如美国的 Fred Hartman大桥和Tacoma大桥,日本的尾道大桥和名港西大桥以及我国广东省佛山市平胜大桥和山东省青岛海湾红岛航道桥等[4]，然而此类设计的桥梁必然导致下部结构成本倍增。而对大跨悬索桥考虑采用双开槽的断面形式，左右对称的开槽正好可以让桥塔塔柱通过，满足了构造上的可行性，也能更好符合对于桥面车道数的需求。

箱梁断面左右对称的双开槽布置，在工程界是首创的结构形式，因此其颤振和涡振性能都有待验证。本文以某跨江悬索桥为背景，进行弹簧悬挂节段模型试验，首先验证两侧开槽对于颤振性能提高的有效性,并对比防撞栏杆基座的有无，从颤振稳定性的角度，给防撞栏杆的设计提出建议。设置不同高度的中央稳定板，研究中央稳定板高度对于此类桥梁的颤振影响。针对试验中发现开槽断面较容易引起桥梁涡振的问题，采用了格栅布置的气动措施，能有效改善涡振性能。最后借助二维三自由度方法分析颤振驱动机理的不同，结合CFD模拟设置格栅前后流场绕流的变化。研究数据结果只针对特定断面尺寸成立，但相关结论为同类型桥梁断面的抗风设计提供系统指导。

1 风洞试验

1.1 试验参数

刚体节段模型的颤振试验在同济大学土木工程防灾国家重点实验室TJ-2号风洞中完成。该风洞试验段的几何尺寸为高2.5 m，宽3.0 m，长15 m，风洞试验风速范围为0～68 m/s。

根据桥梁实际加劲梁断面尺寸，风洞的条件和试验的要求，节段模型设计的几何相似比取为λL=1/100,初始断面模型的截面尺寸见图1。节段模型的材料主要采用金属框架提供刚度，三夹板模拟主梁的气动外形，另外采用ABS塑料模拟防撞栏杆等附属措施，从而保证桥面几何外形的相似性。

图1 初始断面节段模型横截面图(mm)Fig.1 Cross section of prototype deck model(mm)

颤振实验由于其振型间的耦合作用，因此需要严格保证模型的竖弯和扭转频率比相似，对应风速比为λU=5.824，涡振试验可适当放宽频率比的模拟。具体设计参数见表1。

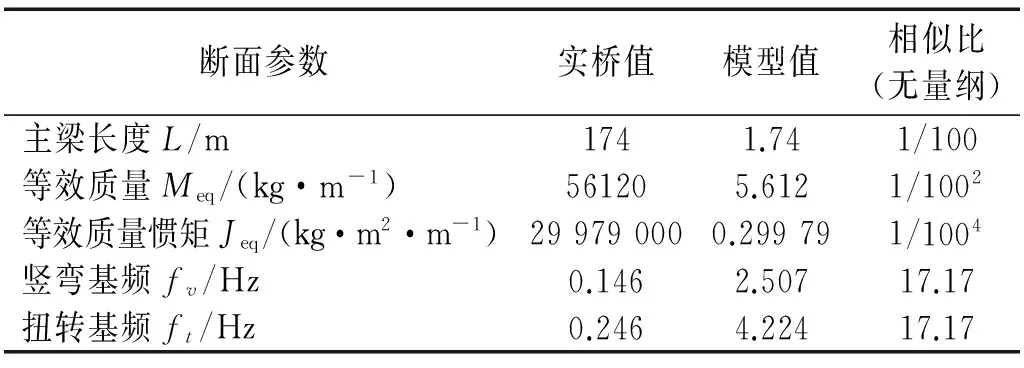
表1 节段模型实验参数

1.2 实验工况

节段模型风洞测振实验在-3°，0°，+3°三个风攻角的均匀流场中进行。

试验阶段首先进行了原始有基座栏杆断面(YJZLG)的颤振实验，并考虑改变防撞栏杆的形式，附加无基座栏杆(WJZLG)和无栏杆工况(WLGSKC)。此外，还设置了五个高度的中央稳定板(ZYWDB)的情况，中央稳定板的高度与梁高的比值在0.55～0.825范围内。由于在颤振较优断面——无基座栏杆(WJZLG)试验中出现了扭转涡激共振现象，考虑采用在开槽处布置均匀间隔的格栅(GS)，主要实验工况见表2。

表2 主要研究内容和工况说明

2 断面颤振性能及影响因素

2.1 双开槽效果说明

为了说明双开槽对于箱梁断面的颤振性能有改善，排除栏杆对颤振性能的影响，研究选取风洞试验主梁断面无栏杆(WLGSKC)情况下三个攻角(+3°，0°，-3°)的颤振临界风速数据，并与采用CFD流固耦合技术模拟得到的理想平板的颤振临界风速，以及用平板颤振导数(三个攻角)做状态空间方法分析得到的临界风速进行比较，得到的结果如表3。

其中，平板0°的颤振导数可根据理论公式计算，其他角度的数据源自CFD模拟。CFD模拟采用二维数值模拟平台“小牛CFD”[6]，该平台基于有限体积方法，在交错网格布置格式、非结构化网格插值算法和动网格大变形算法方面做出了重要创新，并开发了代数多重网格求解器，实现了高数值稳定性、计算精度和计算效率的平衡。计算过程中，综合网格量和计算能力的考虑，空气动粘性系数取实际对应为1.5×10-5m2/s，基于k-ωSST湍流模型进行了二维RANS模拟，并结合Spalding率对壁面网格处的湍粘性进行了修正。流固耦合模拟过程中，等效质量和频率由表1选取，最长模拟时间为1 000 s，当断面振幅超过90°时提前终止模拟。

表3 双开槽无栏杆断面和理想平板颤振临界风速比较

理想平板在0°攻角下的流固耦合模拟对应的扭转位移时程如图2：在来流风速等于16.5 m/s时，结构接近于等幅振动，速度16.6 m/s时运动发散，因此认为颤振临界风速为16.5 m/s。

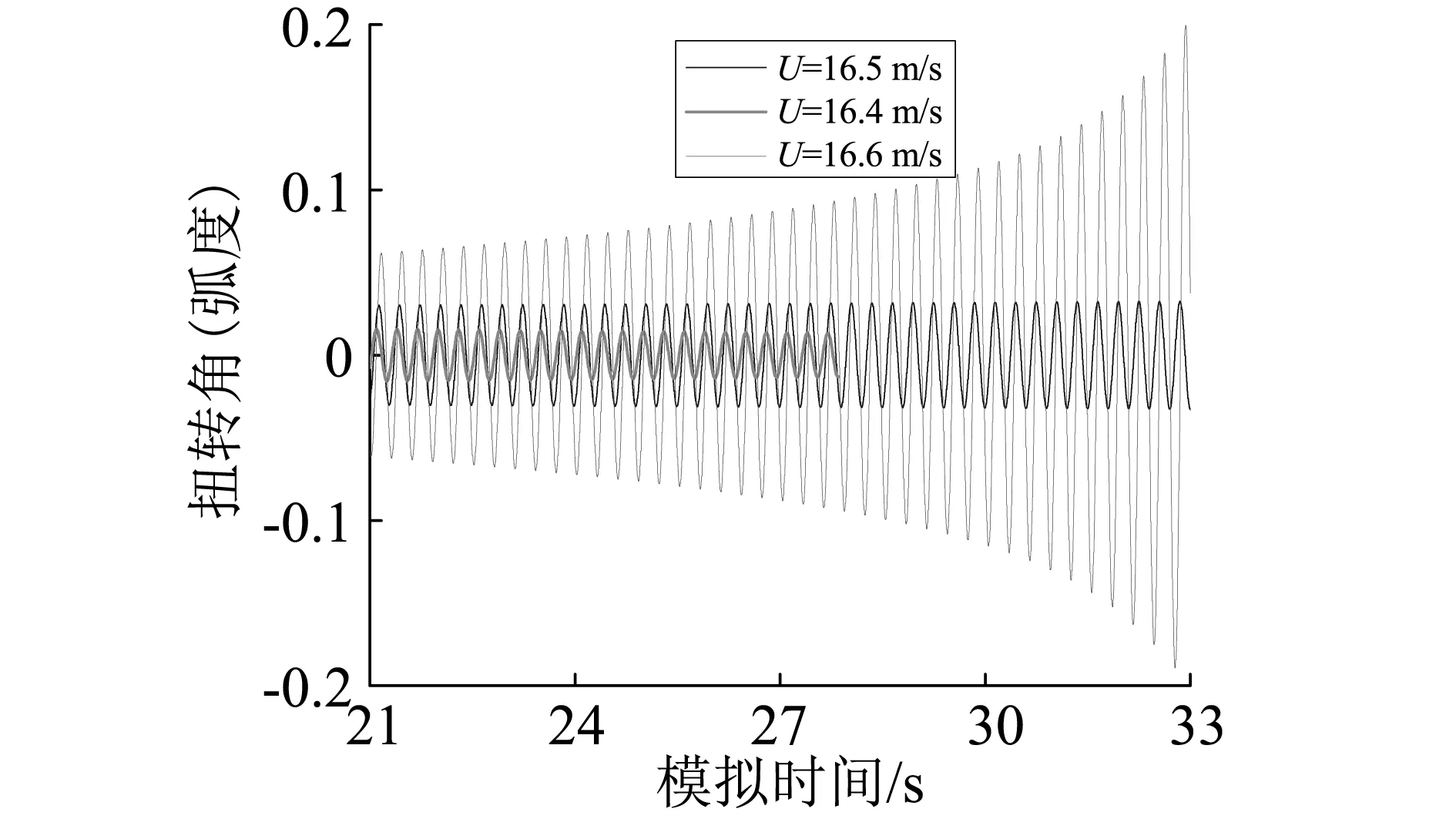
图2 0°攻角下平板流固耦合模拟扭转位移时程Fig.2 Time-history of plate’s torsional displacement (0°)

结合表3中各行数据，流固耦合模拟和状态空间方法计算得到的颤振临界风速吻合的较好，验证了数值模拟方法的正确性及理想平板数据的可靠性。比较无栏杆双开槽断面(WLGSKC)的实验数据和理想平板的数值模拟结果可知，采用双开槽的断面，其三个攻角的颤振临界风速都要明显高于等宽度理想平板的临界风速，而理想平板的颤振临界风速一般视为单箱桥梁断面的上限值。因此，相比于不开槽的情况，采用双开槽的断面能有效改善断面的颤振性能。

2.2 防撞栏杆形式

已有研究发现，不利的基座形式不仅可能激发出涡激共振，而且也会对颤振性能造成负面影响。由于本研究断面形式特殊，因此针对栏杆形式与双开槽断面颤振性能的影响做初步研究。通过风洞试验比较三种工况下的颤振临界风速，得到颤振临界风速结果如表4，比较工况分别为断面采用无基座栏杆(WJZLG)、有基座栏杆(YJZLG)和无栏杆(WLGSKC)的情况(基座的形式如图3)。

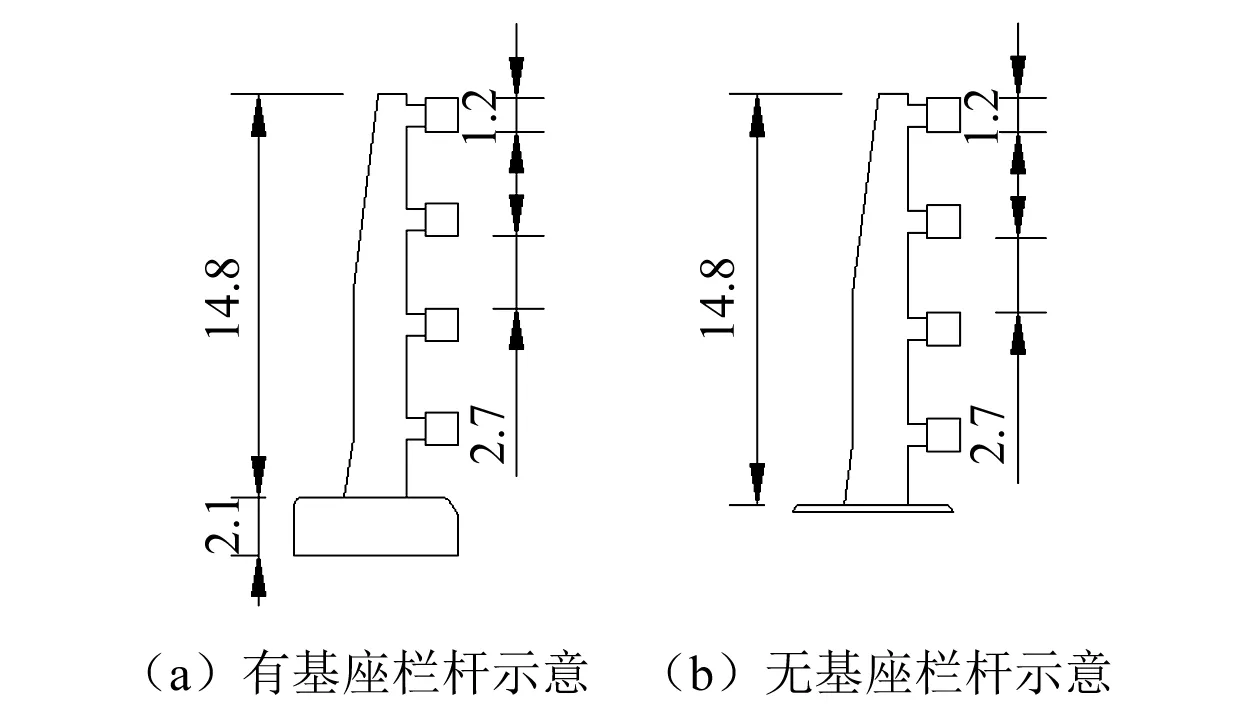
图3 栏杆及基座形式(mm)Fig.3 The shapes of railings and pedestals(mm)

如表4所述，对于双开槽断面的桥梁，颤振性能的最不利工况均出现在+3°攻角。对比WJZLG和YJZLG两种工况，当采用无基座的栏杆时，颤振临界风速大幅度提高，在+3°攻角下，颤振临界风速提高44%。

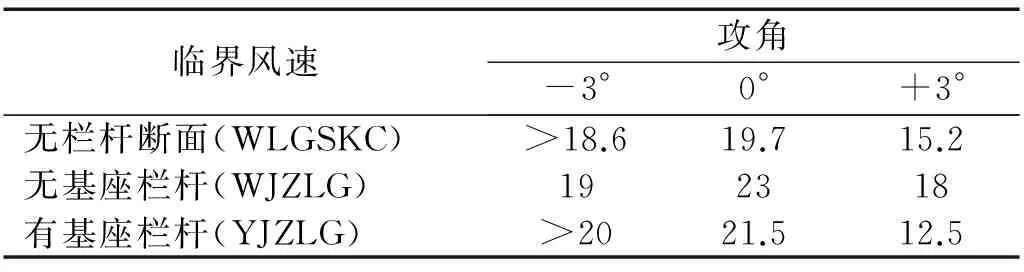
表4 断面不同栏杆形势下颤振临界风速比较

同时，比较WLGSKC和其他两种工况，合适的栏杆形式对断面颤振性能可能起到有利作用。相比于无栏杆的裸桥断面，无基座栏杆(WJZLG)在最不利攻角+3°下，颤振临界风速从15.2 m/s提高到18 m/s，增幅达到18%。

2.3 中央稳定板

在桥梁断面中央设置垂直于桥面的中央稳定板，也是一种有效的颤振控制气动措施，日本的Akashi Kaikyo悬索桥[7]就在桥面下设置了中央稳定板以提高桥梁的颤振临界风速，国内已建成的润扬大桥同样在桥梁上方设置了1.0 m的稳定板。

针对中央稳定板能否对双开槽断面的颤振控制同样有效，以及中央稳定板高度的选取，目前尚无研究。为此，本文比较了原始有基座栏杆断面(YJZLG)设置中央稳定板实桥高度分别为0.55、0.625、0.65、0.75、0.825倍梁高H的情况下最不利攻角+3°颤振临界风速变化规律，如图4。

由图4可知，中央稳定板对于双开槽断面的颤振性能的提高同样有效，且相比于常规的近流线型单箱断面颤振临界风速随着中央稳定板高度增加存在着先增大后减小的规律，双开槽的箱型断面颤振临界风速随着中央稳定板的高度增加而单调增加，试验中没有找到极值点。

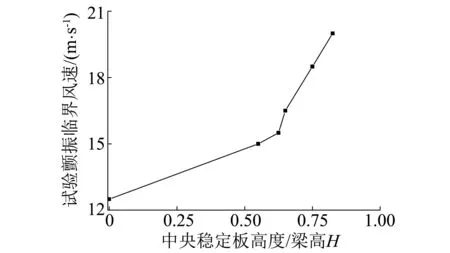
图4 不同中央稳定板高度的颤振临界风速规律(+3°)Fig.4 Critical wind speed for different heights of central stabilizers(+3°)

3 基于二维三自由度的颤振控制机理分析

3.1 二维三自由度方法

根据二维三自由度耦合颤振分析方法(2D-3DOF)[8]的原理，系统扭转运动可以分为两个部分，即扭转自由度的主运动，和基于扭转频率的耦合竖弯运动。其中后者由扭转主运动在竖向自由度上激发而来，它又可以分为两种成分：①扭转运动速度产生的气动升力，对应颤振导数H*2项的气动升力激发的耦合竖向运动；②扭转运动位移产生的气动升力，对应颤振导数H*3项的气动升力激发的耦合竖向运动。两个部分的耦合竖向运动都会进一步形成耦合气动升力矩，(与颤振导数A*1和A*4项对应)，反馈到扭转自由度上与扭转主运动共同影响系统的扭转运动规律。

按照该激励-反馈原理，系统的扭转气动阻尼产生共有5种途径：①扭转运动速度形成的气动升力矩所对应的气动阻尼，为A项；②与“扭转运动速度形成的气动升力，激励得到的竖向运动速度，对应的升力矩”相关的气动阻尼，记为B项；③与“扭转运动速度形成的气动升力，激励得到竖向运动位移，对应的气动升力矩”相关的气动阻尼，记为C项；④与“扭转运动位移形成的气动升力，激励得到的竖向运动速度，对应的气动升力矩”相关的气动阻尼，记为D项；⑤与“扭转运动位移形成的气动升力，激励得到的竖向运动位移，对应的气动升力矩”相关的气动阻尼，记为E项。即：

(1)

式中，Ωαh为无量纲系数。

结合二维三自由度耦合颤振分析结果，对于两种基座形式的栏杆断面及设置中央稳定板的断面，都是系统的扭转运动发散导致的颤振失稳现象，因此深入系统分析扭转运动气动阻尼的发展规律是研究颤振驱动机理的关键。

3.2 栏杆基座对颤振的影响机理

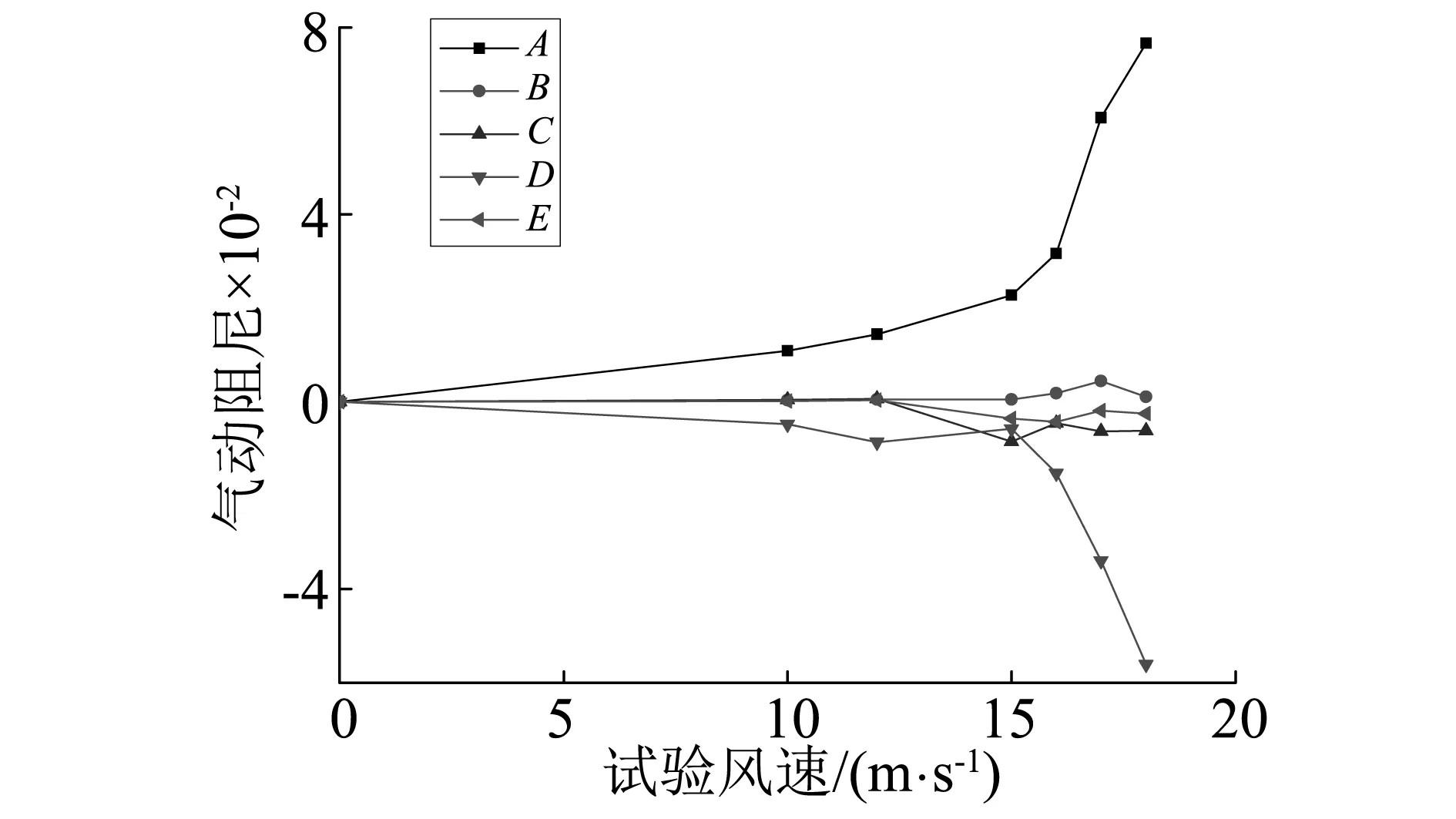
针对无基座栏杆(WJZLG)和有基座栏杆(YJZLG)的+3°攻角(最不利攻角)的试验数据分析其基座形式对于颤振驱动的机理。图5给出了应用二维三自由度耦合颤振分析方法计算得到系统扭转运动气动阻尼各项随风速增加变化规律。由图可知，对两种形式的栏杆，断面都发生了扭转和竖弯自由度耦合效应所产生的气动负阻尼驱动的颤振。其特征是气动阻尼A项(即自身扭转运动项产生的气动阻尼)恒为正值，且随着风速的增大其取值不断增大，对于系统的稳定起着有利作用；而气动阻尼D项为颤振的主要驱动源项，在物理意义上解释为扭转主运动所产生的位移对应的气动升力在竖向激起了耦合竖向运动，该耦合竖向运动的速度对应的气动升力矩反馈到扭转主运动中，形成了激励-反馈的效应，从而导致了系统的颤振发散。

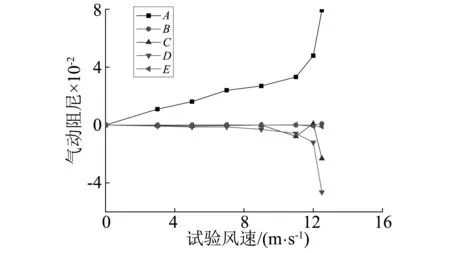
(a) 带基座栏杆(YJZLG)

(b) 无基座栏杆(WJZLG)图5 有无基座栏杆系统扭转气动阻尼变化规律(+3°)Fig.5 Aerodynamic damping of torsion motion for sections with and without railing pedestals(+3°)

在+3°攻角下，比较两种栏杆形式的断面气动阻尼变化规律，YJZLG的变化趋势更为剧烈，如对于A项气动阻尼，在v=12.5 m/s时，YJZLG达到0.079，而WJZLG仅为0.015。同理，不利于稳定的D项气动阻尼，v=12.5 m/s时YJZLG达到-0.046，而WJZLG仅为-0.008。同时，两种断面气动阻尼B和E项均保持着较小值，对于结构颤振发散不起控制作用。颤振稳定的主要控制项A项和主要不利项E项的变化趋势的不同，可以认为是两种形式栏杆下断面颤振临界风速改变的主要原因。

需要指出，对于栏杆带基座(YJZLG)，颤振发散点附近，C项的不利作用增加，即扭转主运动形成的气动升力激励气的耦合竖向运动位移，产生的耦合升力矩对应的气动负阻尼效应突出，当v=12.5 m/s时，该项达到-0.023，而对于无基座栏杆(WJZLG)情况，该部分耦合效应得到有效控制，同等风速下仅为-0.001。可以视为无基座栏杆相对于前者颤振临界风速提高的又一原因。

3.3 中央稳定板对颤振的影响机理

采用二维三自由度方法分析中央稳定板高度为0.55H(ZYWDB-0.55H)和0.625H(ZYWDB-0.625H)时，最不利攻角+3°下的系统扭转运动气动阻尼各项随风速增加变化规律如下图6，对应颤振发散风速分别为15 m/s和15.5 m/s。

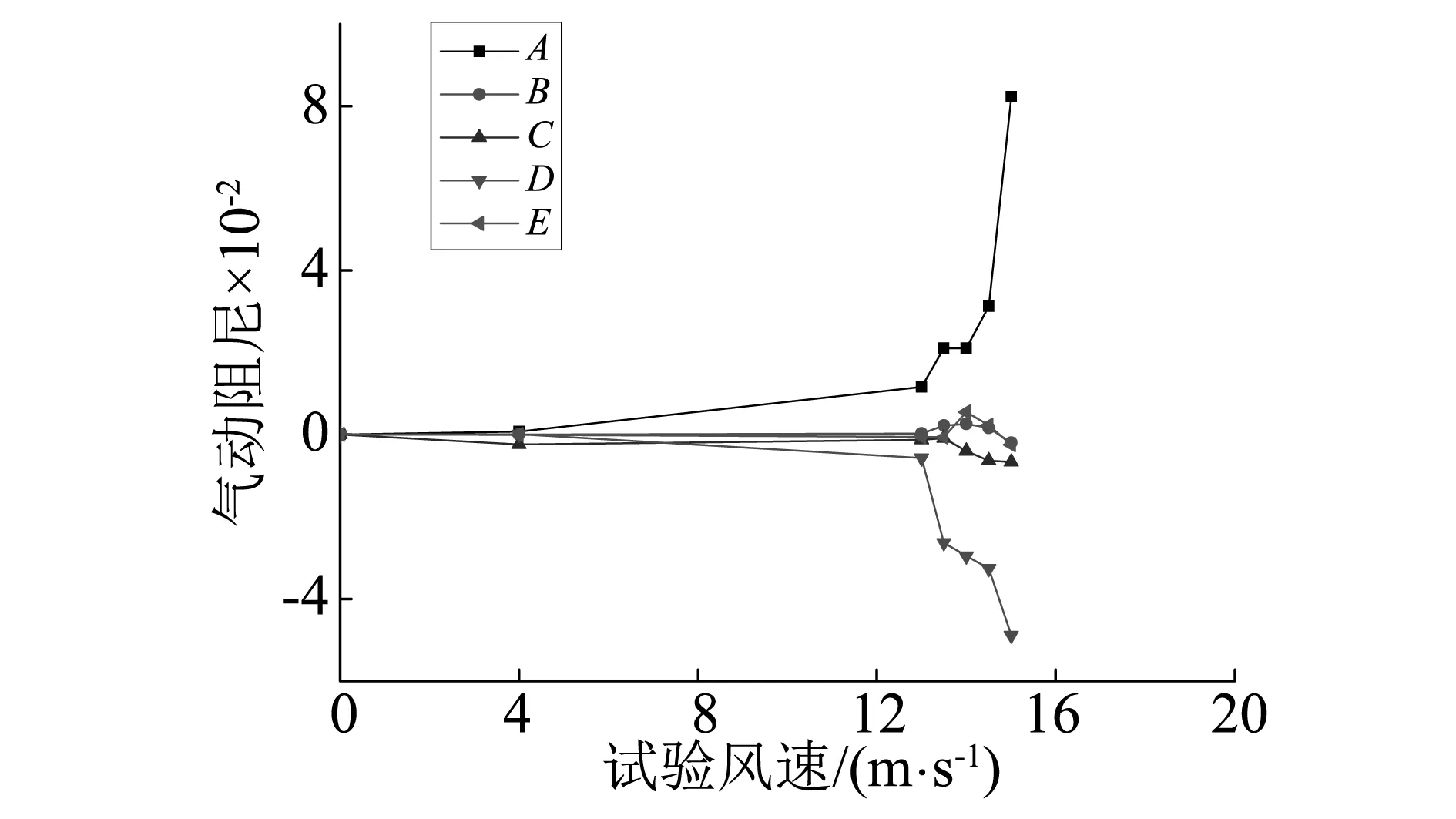
(a) ZYWDB-0.55H气动阻尼(15 m/s发散)

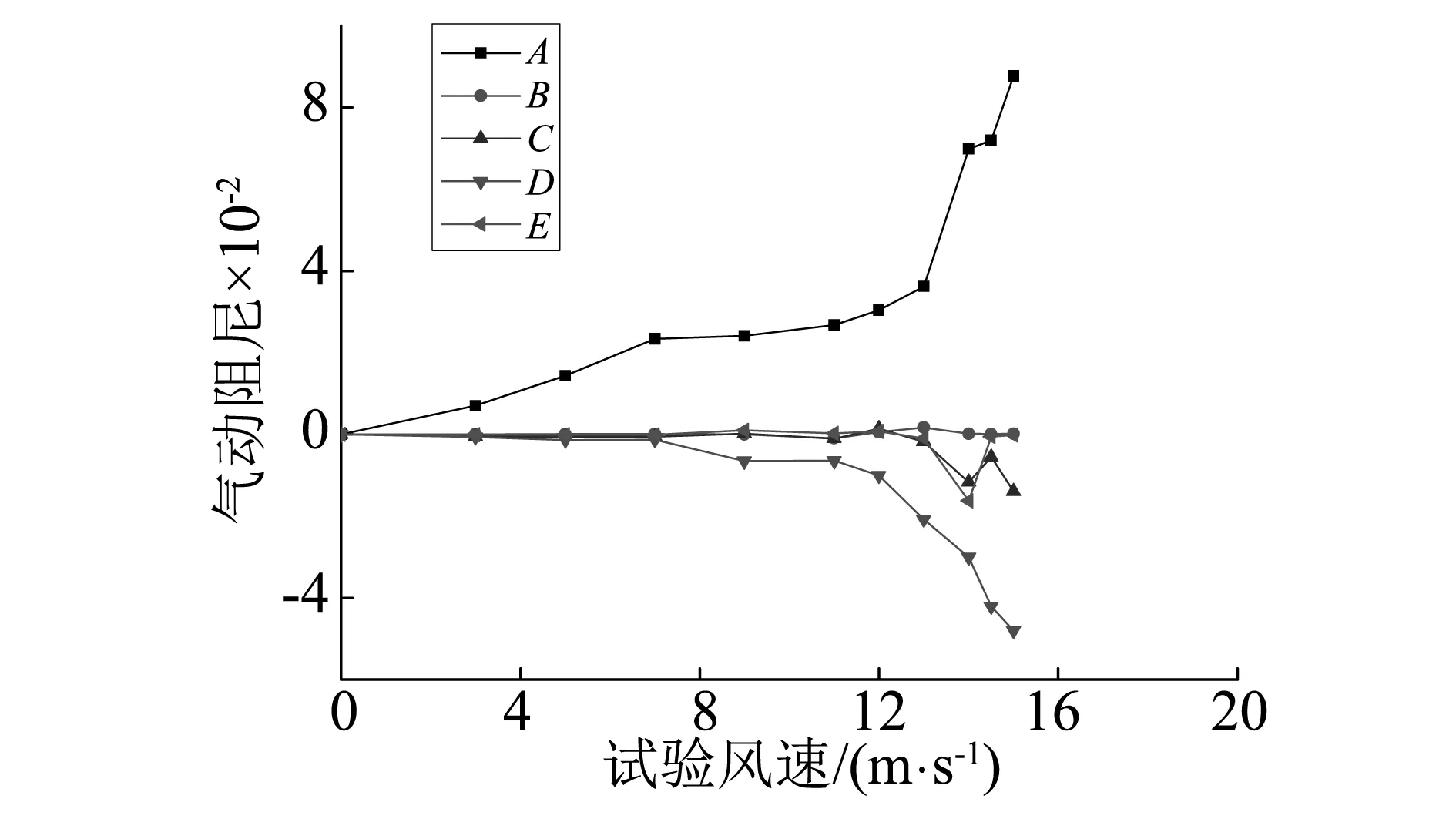
(b) ZYWDB-0.625H气动阻尼(15.5 m/s发散)图6 不同中央稳定板高度的系统扭转气动阻尼变化规律(+3°)Fig.6 Aerodynamic damping for sections with different heights of central stabilizer

通过比较图5(a)和图6，两者的栏杆形式相同(均为原始设计有基座栏杆)，对于设置了较高的中央稳定板，气动阻尼随风速的基本变化趋势类似，即气动阻尼A项始终保持正值，且随着风速的增加而不断增加，气动阻尼D项始终保持着负值，其绝对值随着风速的增大而增大。其余3项，即B、C、E项的参与较小。但相比于原始断面，设置中央稳定板后，气动阻尼的变化速度变慢，如对于YJZLG断面,v=12.5 m/s时A项和D项气动阻尼已经达到0.079和-0.046，而ZYWDB-0.55H分别只有0.011和-0.006。添加中央稳定板后，气动阻尼变化趋势的减缓是断面颤振临界风速提高的基本原因。

对比图6(a)和图6(b)，当中央稳定板高度从0.55H增加到0.625H时，颤振临界风速从15 m/s增加到15.5 m/s。A和D项气动阻尼仍为结构稳定和颤振发散的主要因素，其绝对值随着风速而单调增加，但中央稳定板为0.55H时低风速的气动阻尼取值较小，在颤振临界点附近猛增，而中央稳定板为0.625H时，气动阻尼呈现稳步增长的趋势。如在v=13 m/s时，ZYWDB-0.55H的A和D项气动阻尼为0.012和-0.006，而ZYWDB-0.625H则分别已经达到0.036和-0.021。可以认为ZYWDB -0.55H断面较ZYWDB-0.625H颤振发散更突然。

对于常规的流线型单箱断面，随着中央稳定板高度的增加，颤振临界风速存在着先增大后减小的趋势，同时，在极值点附近，对应着气动阻尼D项由正转负的过程，而本文研究的双开槽断面在试验中未找到极值点，也没有观察到D项的这种变化趋势，且B、C、E项的气动阻尼参与明显小于常规流线型单箱断面，可视为两种断面在颤振驱动机理上的不同之处。

4 断面的涡振控制及机理

4.1 原始断面涡振试验及控制

研究表明，主梁的涡振性能对于附属装置，如栏杆、检修车轨道等位置和形式非常敏感。箱梁断面考虑开槽可以有效提高断面的颤振临界风速，但同时带来了涡激振动的问题，实际西堠门大桥由于开槽后也出现了涡激共振的问题。

在本桥的试验过程中，对于颤振较优栏杆形式——原始断面无基座栏杆(WJZLG)，三个攻角下均出现了涡激共振的现象，类比西堠门桥的结构断面，初步认为是由于开槽引起的该类振动。为了抑制断面的涡激共振现象，考虑了多种控制措施，最终选择在开槽处布置纵向的格栅，宽度为0.12 m，具体位置在横桥向1/4，1/2和3/4槽宽处，见图7。

图7 纵向格栅布置示意图Fig.7 The location of gratings

试验发现，相比于原始断面无基座栏杆(WJZLG)时三个攻角下的扭转涡振，采用如图7所示的格栅(GS)后，对于-3°攻角下，不再有明显的扭转涡振现象，而对于0°和+3°攻角，虽然没有完全消除涡振，但是振幅得到了有效的控制，其具体涡振规律见图8。

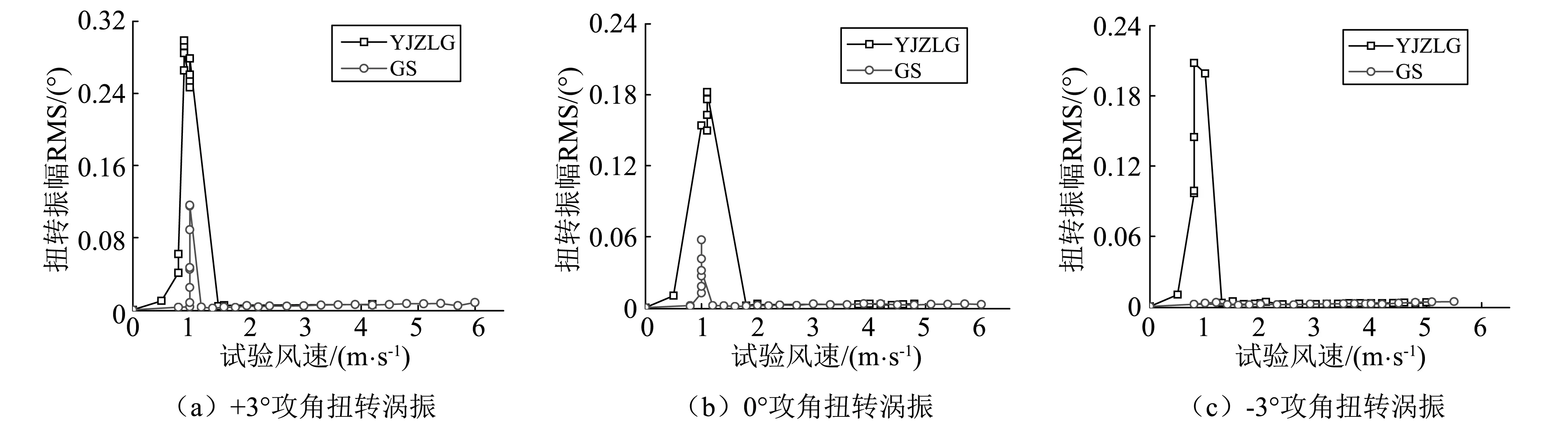
图8 有无格栅时的涡振响应Fig.8 VIV response of bridge decks with or without gratings

由图8可见，对于+3°和0°攻角，原断面涡振锁定区间为0.8～1.4 m/s，通过附加图7所示的格栅，涡振的锁定风速区间明显减小，集中在1.0～1.2 m/s范围内。同时，扭转涡振振幅RMS的最大值减小到原断面(WJZLG)的40%。对于-3°攻角，原始断面扭转涡激振动现象显著，通过附加格栅，能够有效的保证在该攻角下不出现涡振现象。

需要额外指出的是，通过附加格栅的做法，减小了开槽的透风率，对于颤振性能有一定的不利影响，但试验发现，采用上述布置的格栅对颤振临界风速的降低不是特别突出。综合考虑颤振和涡振控制效果，认为在开槽上附加格栅是有效的气动控制措施。

4.2 基于绕流模拟的涡振机理解释

涡振是气流流经钝体结构时产生分离，由此在结构两侧诱导出不对称脱落的旋涡，使结构两侧表面出现交替变化的正负压力而引起的结构横风向有限振幅振动[9]。为研究设置格栅前后断面流场绕流的变化，采用CFD模拟并比较涡振锁定区内流场特性。在CFD计算中，采用LES湍流模型，入口处速度采用Dirichlet边界条件，入口速度控制在1 m/s(锁定区内)，出口速度采用Neumann边界条件；入口和出口的压强边界条件与速度边界条件相反；上下边界采用滑移边界；桥梁壁面以非滑移边界结合Spalding连续型壁面函数实现(近壁面y+≈3)。模拟雷诺数与节段模型试验一致，令结构做扭转强迫振动，振动频率与结构扭频一致，得到稳定状态下不同相位时断面附近流场如图9。

结合试验结果，无基座栏杆断面在该风速下出现了明显的扭转涡振，而在CFD模拟中观察到大规模的单频涡脱。如图9，对比各个相位时无基座栏杆断面的流场特性，该断面的分离点主要三处：迎风侧风嘴处、迎风侧开槽处和背风侧开槽。对于迎风侧风嘴，当相位为0-π/2时，在下侧出现分离泡，漩涡沿着下壁面随风速发展，当相位为π-3π/2时，在风嘴上侧出现分离泡，漩涡沿着上壁面随风速发展。对于迎风侧的开槽，当相位为0-π/2时，在上缘点出现气流的分离；当相位为π-3π/2时，在下缘点出现漩涡并向下发展。对于背风侧开槽，当相位为0-π/2时，下缘处出现较大尺度的漩涡脱落。各处分离效应共同作用，使得上下侧的漩涡交替运动，对应试验中可以观察到结构的扭转涡振。

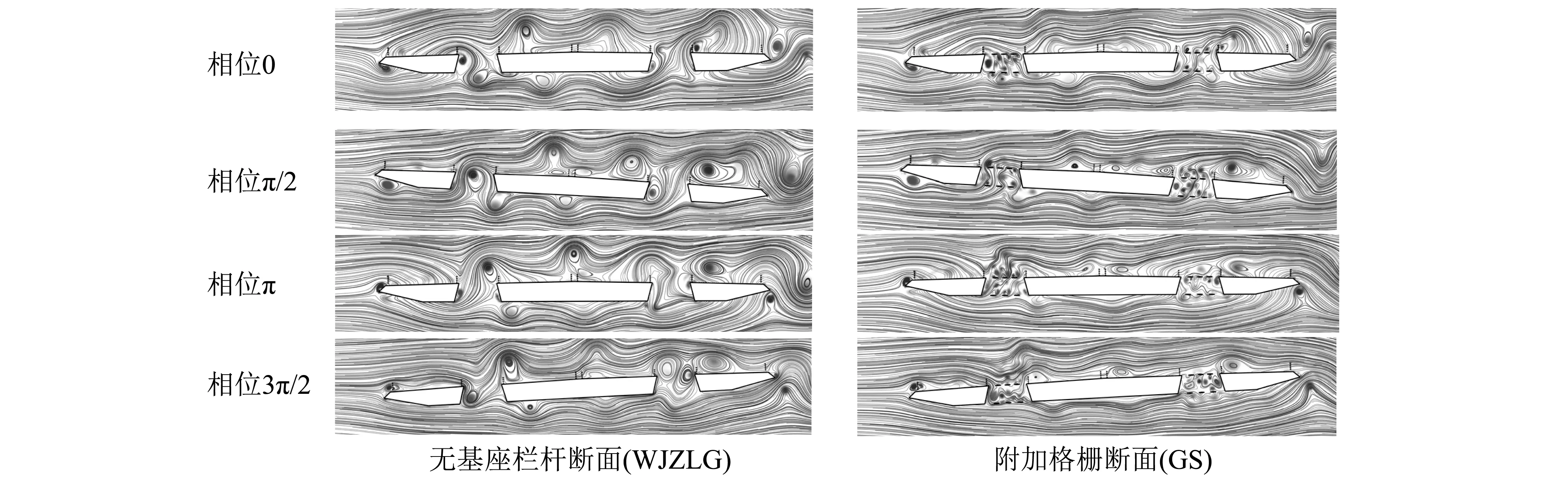
图9 扭转强迫运动断面绕流对比Fig.9 Comparison of flow field with forced torsional vibration

设置等间距格栅后，流场的主要分离点明显减少，只剩迎风侧风嘴。其分离特点与无基座栏杆断面类似，即0-π/2时，下侧出现分离泡，π-3π/2时，上侧出现分离泡。对比加格栅前后，开槽处流场的分离作用明显减弱，未出现大尺度的涡脱。同时，开槽处流场反作用于前侧风嘴处脱落的漩涡，使得该部分漩涡也得不到进一步发展。

需要特别指出，在背风侧开槽下游的栏杆处，也出现了较大尺度的漩涡，其与下游风嘴处形成的漩涡的综合效果，可以推测为图8b中加了纵向格栅后仍有小振幅扭转涡振的原因。

5 结 论

本文针对一双开槽的箱型桥梁断面通过风洞试验结合数值分析，找寻了改善颤振和涡振性能的气动控制措施，并结合二维三自由度方法和CFD模拟，简要总结了颤振及涡振的控制机理。由于对于双开槽断面抗风性能的研究为数不多，因此本文对于实际工程具有很好的借鉴意义。研究得到的主要结论如下：

(1) 双开槽对于箱型断面颤振临界风速的影响类似于单开槽，各攻角下颤振临界风速明显高于同宽度的理想平板。

(2) 以往的研究表明栏杆，检修车轨道等桥梁附属构件对于箱梁断面的涡振性能有直接影响，本文针对双开槽断面发现，栏杆合理形式的选取，也直接关系到颤振性能。采用常规带基座的栏杆，颤振临界风速相比于无栏杆情况有明显的削弱，而采用去除基座的栏杆，颤振性能反而得到大幅度改善。

(3) 提高箱梁断面颤振临界风速的的中央稳定板措施同样适合于双开槽断面。不同的是，常规的单箱断面，中央稳定板存在着最优高度，颤振临界风速随着中央稳定板高度增加先增大后减小。而对于本文研究的双开槽断面，颤振临界风速随着中央稳定板高度单调递增，在中央稳定板为0.825倍梁高时，仍未找到极值点。

(4) 通过二维三自由度研究了栏杆基座、中央稳定板在+3°的颤振发散机理。对于双开槽断面附加上述控制措施，气动正阻尼A项和气动负阻尼D项始终起到控制作用，随着风速的增加，这两项的绝对值也不断增加，合理的气动控制措施体现为减缓增加速度，并在一定程度上减小颤振附近点负阻尼D项的绝对值大小。同时，双开槽断面附加中央稳定板的颤振机理不同于常规单箱断面附加中央稳定板。

(5) 类似于常规单开槽断面，双开槽断面也存在着涡激振动的现象，通过在开槽上布置均匀间隔的纵向格栅，能在不明显降低颤振临界风速的前提下，有效的减小甚至消除涡振，为改善涡振效果的可行手段。结合CFD流场模拟，设置格栅前后断面绕流情况明显改变，格栅阻碍了有规律涡脱的形成。

[1] FALBE-HANSEN K, HAUGE L.Stonecutters bridge—detailed design [C]∥ Proceeding of IABSE Symposium, 2004：112-114.

[2] 葛耀君.西堠门大桥悬索桥抗风性能及风振控制研究[R].上海：同济大学土木工程防灾国家重点实验室，2004.

[3] LARSEN A.Aeroelastic consideration for the Gibraltar bridge feasibility study[M].Bridge Aerodynamics,1998: 165-173.

[4] 于坤，姜美文.青岛海湾大桥红岛航道桥设计和关键技术研究[J] .公路，2009(9)：7-10. YU Kun, JIANG Meiwen. The design and research of key technology of Qingdao Bay Bridge[J]. Highway, 2009(9): 7-10.

[5] 郭增伟，葛耀君.桥梁自激力的状态空间模型的时频特性[J].振动工程学报，2013，26(2)：199-206. GUO Zengwei, GE Yaojun.Time and frequency response characteristics of self-exited force of bridge in state space domain[J]. Journal of Vibration Engineering, 2013,26(2): 199-206.

[6] 刘十一.大跨度桥梁非线性气动力模型和非平稳全过程风致响应[D].上海:同济大学,2014.

[7] 项海帆.现代桥梁抗风理论与实践[M].北京：人民交通出版社，2005：206-226.

[8] 杨詠昕.大跨度桥梁二维颤振机理及其应用研究[D].上海：同济大学,2002.

[9] 罗东伟. 开槽箱梁涡激振动及其控制措施研究[D].上海：同济大学,2013.

Wind resistance performance of a double-slotting suspension bridge andits aerodynamic control measures

XIA Jinlin, CAO Fengchan, GE Yaojun

(State Key Laboratory of Disaster Reduction in Civil Engineering ,Tongji University, Shanghai 200092, China)

To understand the flutter and vortex-induced vibration(VIV) performance of the bridge deck with double-slot and to propose feasible control measures, a sectional wind tunnel test was carried out on a steel-box suspension bridge being planned. An analysis based on a 2 dimension-3DOF (2D-3DOF) model and a CFD simulation were introduced respectively to understand the flutter and VIV mechanisms. The results show that, the double-slotting is an effective method to improve the flutter performance of the steel-box deck.The type of railings, i. e., with or without pedestal, influences the critical wind speed significantly. Besides, the central stabilizer, as a conventional control alternative, also has a positive impact on the bridge’s stability. In a certain range , the height of the stabilizing plate has positive correlation with the stability. As shown by the 2D-3DOF method, both the central stabilizer and optimized railing can slow down the changing tendency of aerodynamic damping with the changing of wind speed. Since the VIV often occurs on a slotting deck, various measures have been taken into account in the test, while the equidistant grating is proved to be more efficacious. By the CFD simulation, it is found, the essential mechanism is that the grating changes the flow field notably so as to avoid the large-scale vortex shedding.

double-slotting; flutter; aerodynamic control; wind tunnel test

土木工程防灾国家重点实验室“973计划”项目(2013CB036301)

2015-12-07 修改稿收到日期： 2016-02-09

夏锦林 男，博士生，1991年6月生

葛耀君 男，博士，教授，1958年6月生

U 441.3;V 211.7

A

10.13465/j.cnki.jvs.2017.10.012