基于正交设计的输电线路覆冰不平衡张力影响因素的研究及应用

龚 磊，郑 炜，郭 恒，秦 榛

（重庆电力设计院，重庆401121）

基于正交设计的输电线路覆冰不平衡张力影响因素的研究及应用

龚 磊，郑 炜，郭 恒，秦 榛

（重庆电力设计院，重庆401121）

摘 要：为研究多因素作用下的输电线路覆冰不平衡张力，利用正交设计法开展了档距、高差、导线安全系数以及绝缘子串长对导线不平衡张力影响的研究。正交实验结果趋势图表明，最大不平衡张力与串长呈负相关关系，与高差、档距、导线安全系数呈正相关关系；极差分析表明，档距对不平衡张力影响的程度最大，其次是高差、导线安全系数，绝缘子串长的影响最弱。最后以实际工程为例，将正交设计法得出的规律用于覆冰线路的优化设计，经优化，线路最大不平衡张力百分数由原来的27．07%降为23．80%，表明本文得出的规律具有工程使用价值。
关键词：输电线路；不均匀覆冰；不平衡张力；正交设计；优化设计
中图分类号：TM752 文献标识码：A 文章编号：1008-8032（2017）02-0038-04

输电线路不均匀覆冰会使得耐张段内各档应力不一致，从而造成直线杆塔两侧出现不平衡张力，使铁塔承受弯矩和扭矩，当不平衡张力值比较大时，杆塔会损坏或倒塌［1］。2008年的冰雪天气引发了大量的断线倒塔，给国家电网造成了巨大损失［2－3］。事后分析表明，不均匀覆冰所产生的纵向不平衡张力是断线倒塔的原因之一［4］。

一直以来，输电线路覆冰不平衡张力获得了广大科技人员的关注。文献［5］以超／特高压交流同塔多回输电线路为依托，建立了“塔－线－串”耦合的有限元模型；文献［6］研究了覆冰加载模式、偏心等因素对特高压直线塔不平衡张力的影响；文献［7］分析了湖南500 kV岗云线175－177号倒塔事故；文献［8］计算了“溪洛渡左岸－浙江金华”±800 kV特高压直流线路中某耐张段的不平衡张力，并根据计算结果给出相关建议；文献［9－11］对不平衡张力数学模型中方程组的解法进行研究，提出了许多新方法；文献［10－13］对影响不平衡张力的因素作了单因素敏感性分析。

进行多因素综合作用下的输电线路覆冰不平衡张力研究，有助于更好地指导覆冰线路优化设计。影响不平衡张力的因素较多，它们均存在一定的变化范围。如进行各因素各水平下的全面实验，实验次数将随因素类数以及因素水平数的增多而急剧增大。正交设计法能够简化各因素的组合，具有实验工作量少、信息量丰富的优点［14］。本文选取档距、高差、导线安全系数以及悬垂绝缘子串长这4类因素，并结合工程实际确定各因素变化范围。然后，利用正交设计法开展全面研究，并对实验结果做趋势图分析和极差分析，以获取不平衡张力与各因素之间的变化规律以及各因素对不平衡张力影响程度的大小。最后，将得出的规律用于工程实例，以指导覆冰线路的优化设计。

1 输电线路覆冰不平衡张力的数学模型

导线不均匀覆冰情况下的不平衡张力模型可概括为3类方程组：第一类为档距变化与导线应力之间的方程；第二类为悬垂绝缘子串偏移与杆塔两侧导线应力之间的方程；第三类为各档档距变化量之间关系的方程［15］。

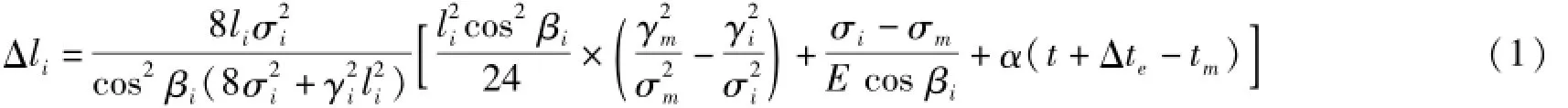
1）第一类方程为式中：li，βi分别为悬垂绝缘子串处于中垂位置时的第i档档距、高差角；Δli，σi，γi分别为第i档的档距变化量、档内应力以及导线比载；tm，γm，σm分别为架线时的气温、导线比载以及架线气温下的导线水平应力；Δte为补偿导线初伸长所采取的等效温度；E，α分别为导线的弹性系数、温度线膨胀系数。

2）第二类方程为式中：Gi，λi分别为第i基直线塔上的绝缘子串荷载及串长；N为子导线根数；A为导线截面积；σi，σi＋1分别为第i，i＋1档的档内应力；γi，γi＋1分别为第i，i＋1档的档内导线比载；δi为第i基直线塔上导线悬挂点沿线路方向的水平偏移距离；li，βi，hi，li＋1，βi＋1，hi＋1这6个参数均为悬垂绝缘子串处于中垂位置时的参数，依次为第i档的档距、高差角，第i基塔的导线悬挂点对第i－1基的高差，第i＋1档的档距、高差角，第i＋1基塔的导线悬挂点对第i基的高差。

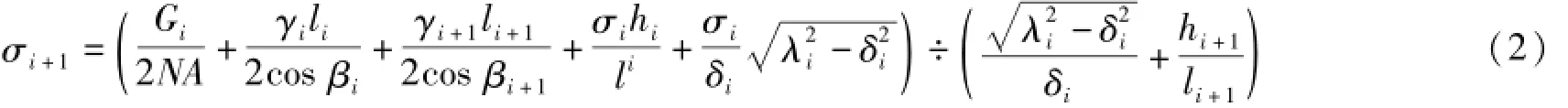
3）第三类方程为

该方程表明对整个耐张段而言，各档档距增量之和为零。

设耐张段共含n档，则第一类方程组由n个方程组成，第二类由n－1个方程组成，第三类含1个方程，共2n个方程。其中，σ，Δl为未知数，共2n个，与方程数一致，故可求解出各未知数。

2 正交实验

2．1 相关参数

不均匀覆冰情况下，不平衡张力计算模型采用文献［6］中的模式2，即等连续档，仅中间1基杆塔与相邻杆塔存在高差。设耐张段含7档，其中前4档覆冰率为100%，后3档按30%设计，仅第4基直线塔高于前后塔。实验对象为220 kV线路，处于20 mm重冰区，导线选用2JLX／G1A－400／50钢芯成型铝绞线。本文选用的影响因素为档距、高差、导线安全系数以及悬垂绝缘子串长。

1）重冰区线路的档距取值不宜过大，取值过小则经济性较差，故将档距的取值范围定为300～450 m，每隔50 m取一个值。

2）处于斜坡上的塔位，当其在某一固定位置左右移动时，不仅会导致与相邻杆塔间的档距发生变化，还会引起彼此间的高差发生变化，故高差的变化量应结合档距变化量进行考虑。上面介绍到档距变化量为50 m，以地形坡角为20°左右进行考虑，高差变化量取为20 m。另将基础高差取为40 m，则高差的变化范围为40～100 m。

3）相关规程规定，导线在最低点的安全系数不低于2．5［16］，取值过大则将引起弧垂过大，故将安全系数的取值范围定为2．5～2．8。

4）相关规程规定，220 kV线路悬垂绝缘子串的绝缘子最少片数为13片［16］。单片绝缘子的结构高度取0．146 m，净重6 kg。本文绝缘子片数取13～16片，对应的串长变化范围为2．353～2．791 m，串重变化范围为105．8～123．8 kg。

2．2 正交表

本文选取的4类因素均含有4种水平，各因素及其水平见表1。

表1 各因素及其水平表

正交表一般用Lm（an）表示。其中：L为正交表代号；m为正交表的行数，同时也代表着实验的总次数；a为因素水平数；n为正交表列数，也表示最多能安排的因素种类数，一般要求n≥a。鉴于本文各因素均含有4种水平，故选用常用正交表L16（45）。其中，第1列为误差列，其余4列分别对应A，B，C，D这4类因素，见表2。如进行全面实验，则实验次数为44＝256次，采用正交设计后实验次数降为16次。

表2 正交表

2．3 实验结果及分析

将表2中16组实验所对应的参数分别代入到第一节所介绍的数学模型中求解，得到不均匀覆冰情况下的各档档内应力，相邻两档档内相对应力差即为不平衡张力百分数。最大不平衡张力百分数能够反映不均匀覆冰对耐张段造成的最坏影响，故将其作为评价指标，实验结果如表3所示。

表3 实验结果

以因素水平为横轴，同一因素各水平下最大不平衡张力百分数的平均值为纵轴，分别绘制各因素与评价指标之间的趋势图，如图1所示。由图1可知，最大不平衡张力百分数随档距、高差以及导线安全系数的增大而增大，随绝缘子串长的增大而减小，该规律为覆冰线路的优化设计提供了依据。由于同一因素各水平下评价指标平均值的极差能够反映出水平变动对实验结果的影响程度，故对正交实验结果做极差分析，以获取各因素对最大不平衡张力影响的大小。极差分析结果如表4所示。由极差R的大小可知，各因素的影响程度从高到低依次是：档距、高差、导线安全系数、绝缘子串长。

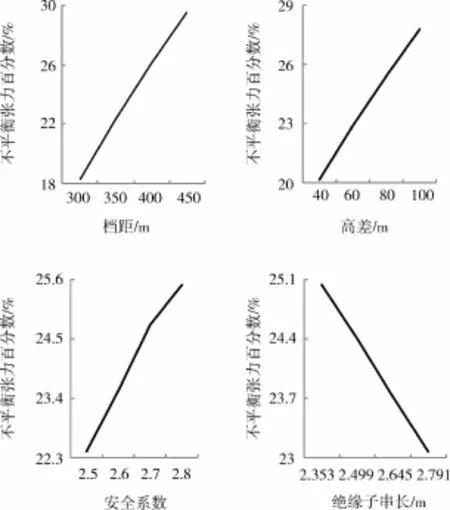
图1 各因素与评价指标的趋势图

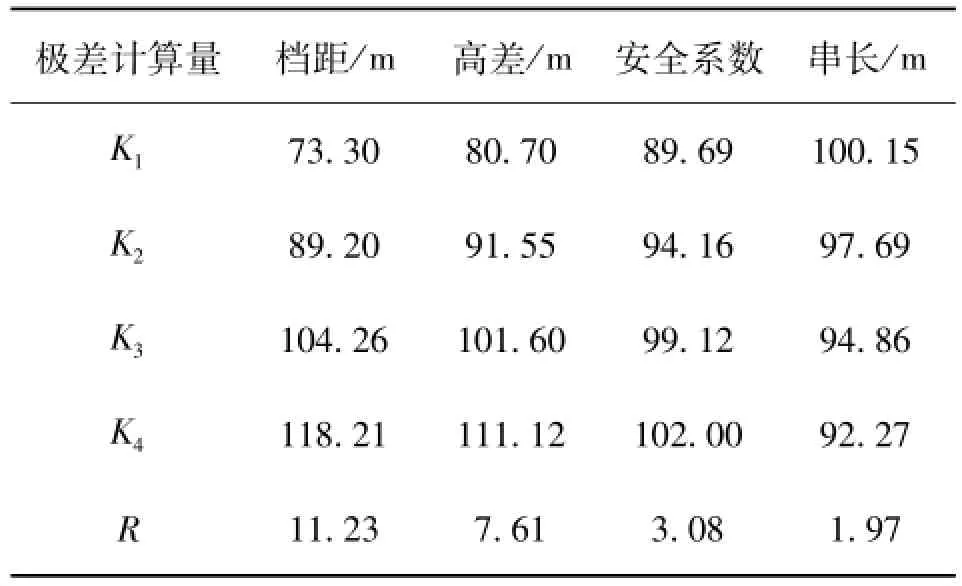
表4 极差分析表

3 工程实例

以西南地区某220 kV工程为例，其中排好塔位的某一耐张段平断面如图2所示，塔位信息见表5。该耐张段气象条件、导线型号与2．1小节一致，悬垂绝缘子片数为13片，导线安全系数为2．7。

图2 优化前平断面图

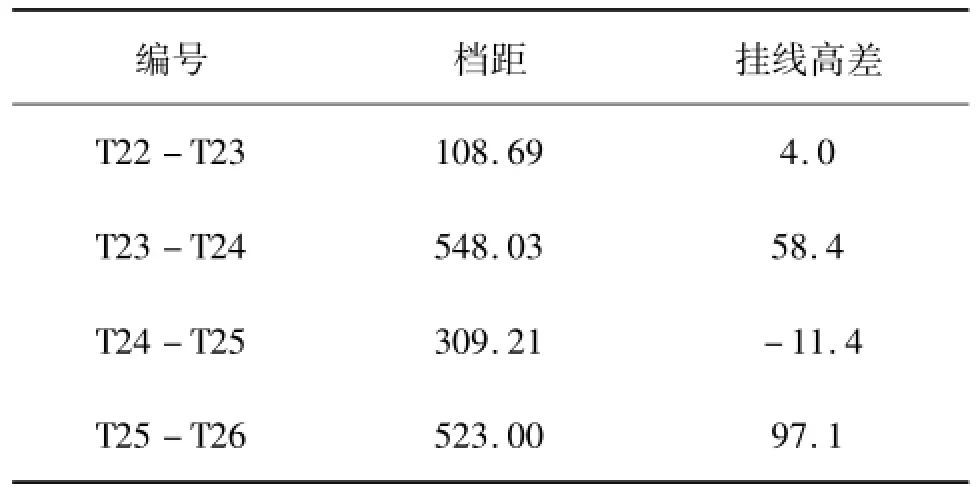
表5 优化前的塔位信息m

仍以一侧100%覆冰，另一侧30%覆冰考虑，逐档校验优化前断面的覆冰不平衡张力。当不均匀覆冰分界点在塔T24时，最大不平衡张力出现在塔T24两侧，达27．07%，大于规范中所规定的取值25%［17］，有必要对该耐张段进行优化。

鉴于实际最大不平衡张力百分值仅比规定值高2．07%，优先考虑较易实现的导线安全系数以及绝缘子串长调整。该耐张段处于20 mm冰区，出于适当放松导线应力角度，本次优化不对导线安全系数进行调整。增加悬垂绝缘子串长可降低不平衡应力，但绝缘子片数增多，可能会导致塔头尺寸变大、横担变长。因此，绝缘子片数不宜过多，本次优化采用15片绝缘子。再进行逐档校验后发现，最大不平衡张力仍高于规定值，为25．26%，有必要对档距或高差进行优化。

档距与高差往往是一起变化的。优化档距时可能会使得高差增大，由于两者变化方向不一致会导致对不平衡张力的作用效果相反，所以有必要明确综合作用下的不平衡张力的变化方向。根据极差分析得出的结论可知，档距对不平衡张力的影响程度要大于高差，故优化时可暂时忽略高差的影响。由前面叙述可知，本次需优化的幅度较小。同时，由图2和表5可知，塔T23与塔T24之间的档距较大，故将塔T24向塔T23方向调整，其他杆塔不做调整。受对地安全距离限制，塔T24的呼高需增大6 m，优化后的平断面如图3所示，塔位信息见表6。

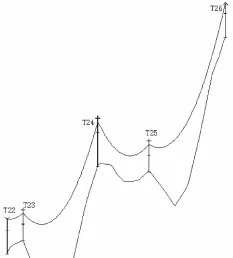
图3 优化后平断面图

表6 优化后的塔位信息m

优化后的最大不平衡张力出现在塔T24两侧，为23．80%，比优化前小3．27%。对比表5与表6可知，优化后的高差有所增大，但最大不平衡张力仍得到降低。这表明在优化过程中，当档距与高差发生矛盾时档距起主导作用。

4 结论

1）可采用减小较大档档距、降低挂线高差、降低导线安全系数以及增加绝缘子片数的方法来降低输电线路纵向不平衡张力。

2）档距对不平衡张力的影响最为显著，其次是高差，导线安全系数和悬垂绝缘子串长的影响相对较弱，优化时可根据实际情况进行针对性调整。

［1］ 张子引，刘学军．架空输电线路连续档不平衡张力计算［J］．电力建设，2009，30（5）：32－34．

［2］ 陆佳政，胡建平，方针，等．雪峰山脉小沙江自然灾害试验场覆冰与融冰实验［J］．高电压技术，2014，40（2）：388－394．

［3］ 陈吉，蒋兴良，郭钢，等．交直流电场对雨凇覆冰特性的影响研究［J］．电网技术，2015，39（3）：867－872．

［4］ 李庆峰，范峥，吴穹，等．全国输电线路覆冰情况调研及事故分析［J］．电网技术，2008，32（9）：33－36．

［5］ 韩军科，杨靖波，李清华，等．超／特高压交流同塔多回输电线路覆冰不平衡张力分析［J］．电网技术，2011，35（12）：33－37．

［6］ 杨风利，杨靖波，张子富．重覆冰区特高压悬垂型杆塔不平衡张力分析［J］．电网技术，2012，36（3）：234－240．

［7］ 刘庆丰．输电线路不平衡张力分析和计算［J］．电力自动化设备，2006，26（1）：93－95．

［8］ 宋刚，张彤．特高压直流输电线路直线塔重覆冰不平衡张力计算［J］．电力自动化设备，2014，34（7）：119－123．

［9］ 李军，彭谦，康东升．改变步长的输电线路不平衡张力计算方法［J］．电力建设，2010，31（12）：26－29．

［10］薛志方，程思勇．置信域算法在输电线路覆冰不平衡张力计算中的应用及不平衡张力的影响因素［J］．电网技术，2012，36（4）：225－228．

［11］杨博，郎需军，杨茂亭，等．重覆冰区线路不均匀脱冰的不平衡张力计算［J］．电力建设，2014，35（10）：52－57．

［12］程思勇，薛志方．覆冰不平衡张力计算分析［J］．电网与清洁能源，2011，27（2）：10－13．

［13］卢本初，程思勇，何民．纵向不平衡张力计算与分析［J］．广西电力，2011，32（6）：89－92．

［14］赵睛川，李建生，渠富元，等．正交试验法在燃煤电站锅炉燃烧优化中的应用［J］．华东电力，2008，36（8）：80－84．

［15］张殿生，倪宗德，张洞明，等．电力工程高压送电线路设计手册［M］．2版．北京：中国电力出版社，2003：202－205．

［16］国家能源局．重覆冰架空输电线路设计技术规程：DL／T 5440—2009［S］．北京：中国电力出版社，2009．

［17］中华人民共和国住房和城乡建设部．110～750 kV架空输电线路设计规范：GB 50545—2010［S］．北京：中国计划出版社，2010．

A Study on the Influencing Factors of Unbalanced Tension of Ice-Covered Transm ission Lines Based on the Orthogonal Design and the Application

GONG Lei，ZHENGWei，GUO Heng，QIN Zhen
（Chongqing Electric Power Design Institute of State Grid Chongqing Electric Power Company，Chongqing 401121，P．R．China）

In order to research the unbalanced tension of ice-covered transmission lines subject to various factors，a study on the influence of the span，the heightbetween towers，the safety coefficientofwires and the length of the insulator chain on the unbalanced tension has been implemented bymeans of the orthogonal designmethod．The tendency chart of the experimental results has shown that the maximum unbalanced tension has a negative correlation with the length of the insulator chain and has a positive correlation with the height between towers，the pan and the safety coefficient of wires．The results of the range analysis have shown that the span influences the unbalanced tension to the greatest degree，the influence of the height between towers and the safety coefficient decreases progressively，and the influence of the length of the insulator chain is theweakest．Taking an actual project for example，the laws derived from the orthogonal design method have been applied in the optimization design of ice-covered transmission lines．The maximum unbalanced tension percentage has been reduced from 27．07%to 23．80%，which proves the engineering practicability of the laws in this study．

transmission lines；nonuniform ice-coating；unbalanced tension；orthogonal design；optimized design

2016－11－03

龚 磊（1988－），工程师，研究方向为输电线路设计及线路防冰。