复合材料层合板装配精度影响因素研究

（航天材料及工艺研究所，北京 100076）

复合材料具有密度低、比强度高、比刚度大等特点，在实际生产中的应用越来越广泛[1]。由于零件、夹具和装配过程总是存在误差，当复合材料零件装配到一起后，最终的装配体不可避免地会存在误差。由于复合材料层合板属于薄板类零件，因此，研究人员首先从薄板类零件装配精度分析入手进行研究。Jin和Shi[2]以及Ding等[3]首先提出了刚性钣金类零件二维装配的状态空间模型来预测装配精度，得到了刚性二维钣金零件的装配精度主要受零件加工误差的影响。Liu等[4]通过将工程结构力学和统计方法结合起来，提出一种“补偿单元法”，分析一维柔性钣金件装配误差的影响因素为零件在加工过程中的变形误差。Liu等[5]通过使用有限元法构建了联系零件加工误差和装配误差的“敏感矩阵”，将模型进一步扩展到可适用于二维或三维自由曲面的柔性钣金类零件，该方法称为“影响系数法”，于是，得到了柔性二维或三维钣金零件变形误差与装配误差之间的关系。Camelio[6]和Hu等[7]借用“误差流”理论[2]，进一步将“影响系数法”的模型扩展到柔性钣金类零件的多工位装配过程，进而分析出了三维钣金零件的装配误差除了受到零件的加工误差影响外，还受到装配过程中的定位误差影响。然而，在Camelio等[6]的模型中，假设所有误差是彼此独立的。然而，这种误差源独立假设并非总是合理的。例如，方形钣金件的4个交点的翘曲误差是彼此相关的。继而，Camelio等[8]介绍了误差源的几何协方差对考虑误差独立性的柔性零件装配误差的影响。最终得到了考虑零件变形误差相关性的柔性钣金零件误差对装配误差的影响，Lin等[9]针对大尺寸的钣金零件，例如航空宇航或船舶中用到的零件，分析了装配误差，最终发现，对于大尺寸钣金零件，除了零件加工变形对装配精度产生重要影响外，零件受重力影响而产生的变形对装配精度的影响也不可忽视。

上述各研究都是针对钣金类零件的装配精度分析，不同于金属零件，复合材料具有各向异性的力学特性，因此，上述研究不适用于复合材料层合板装配精度分析。针对上述问题，Dong等[10]提出了一个基于“响应面法”的方法，建立了一个回归模型，该模型借助于虚拟试验和有限元分析来揭示零件误差和装配误差之间的关系。该方法通过设计大量的零件误差情况，并反复进行有限元分析计算装配误差，最后通过“响应表面法”构建零件误差与装配误差之间的“黑盒子”模型。

导致装配误差的主要因素为零件的加工误差。在实际生产中，由于受限于设备的加工能力或考虑到生产成本等因素，往往无法通过提高加工精度来改善系统的装配精度。于是，可以考虑通过调整装配工艺参数来优化装配精度。本文将分别分析零件的配对组合形式和装配顺序对装配精度的影响，并根据装配精度的仿真计算结果优化装配工艺参数，指导实际装配，以得到最佳的装配精度。

1 复合材料层合板装配过程

1.1 复合材料层合板多工位装配过程

“3-2-1”准则是刚性零件装配的常用定位方式，然而，对于柔性零件需要采用“N-2-1”定位方式[11]来防止过变形。考虑零件边缘的翘曲误差，3块复合材料层合板两工位装配过程可分为如图1所示的11个装配步骤，其中，点划线表示上一装配步骤中结构状态。

1.2 复合材料层合板多工位装配过程有限元仿真分析

采用ANSYS有限元仿真软件进行复合材料层合板多工位装配过程中结构变形的仿真分析。零件的尺寸参数和材料参数分别如表1、2所示。通过MATLAB为每个关键点各生成100组误差源，连接点、夹紧夹具点和测量点的加工误差服从正态分布（μ=1mm，σ=0.3mm，样本容量n=100）。

基于前面针对复合材料层合板多工位装配过程的介绍，以生成的误差源中任选的一组误差值为例，对每个装配步进行相应的有限元仿真分析，在分析中，选择shell181单元，根据每个装配步的定位和装配方式，设定边界条件和施加外载荷，得到的结构变形情况如图2所示。

2 零件配对组合方式对装配精度的影响

零件的加工误差影响了最终产品的装配精度。在不依赖于提高零件加工精度的情况下，考虑通过调整装配工艺参数来改进产品的装配精度，如优化零件的配对组合形式。实际生产中，很多产品并非单件生产。因此，可以将同类零件编号并进行重新配对组合，通过有限元仿真计算不同组合形式下的装配精度。表3中给出了生成的误差源中的任意两组误差值，即为零件1、零件2和零件3分别选择两组误差值。

对上述两组装配体中的零件进行重新配对组合，所有组合方式如表4所示。

采用前述计算装配精度的有限元仿真方法，得到装配后关键点的误差值如表5所示。

对比表5中4种组合方式下的装配体1和装配体2的装配精度，可以发现，对于装配体1中的测量点和采用第1种零件组合方式可以得到最佳的装配精度；对于装配体1中的测量点采用第2种零件组合方式可以得到最佳的装配精度；对于装配体2中的测量点和采用第4种零件组合方式可以得到最佳的装配精度；对于装配体2中的测量点采用第3种零件组合方式可以得到最佳的装配精度。因此，在实际生产中，可以根据产品性能对各测量点精度的依赖程度，设置相应的权重系数，对不同组合方式下产品的装配精度进行综合评定，选择最佳的装配组合方式。

3 零件装配顺序对装配精度的影响

在实际生产中，有些组件的装配顺序是可以调整的。例如，图1中的3个零件既可以按照图1的装配顺序来进行装配，即先装配零件1和零件2组成子装配体，再将该子装配体与零件3进行装配，得到最终的装配体，定义为1-2-3的装配方式；也可以先将零件3和零件1进行装配组成子装配体，再将该子装配体与零件2进行装配，定义为3-1-2的装配方式。由于这类装配需要借助夹具来完成，不同的装配顺序往往需要对零件采用不同的定位方式。对于带有误差的零件来说，采用不同的定位方式会使零件显示出不同的误差。例如，图1中的3个零件采用上述两种不同的装配顺序时，零件1需要采用图3（a）、（b）两种不同的定位方式。根据第1种定位方式下零件的加工误差可以计算出第2种定位方式下零件的加工误差。具体计算方法如下：由于这里不考虑夹具的位置误差，因此，可以过第2种定位方式下的3个定位点建立1个平面xoy，如图4所示，其他各关键点到该平面的距离（带有正负）即为第2种定位方式下各关键点的误差。假设第1种定位方式下各关键点的加工误差如表6所示，那么，当采用第2种定位方式时，各关键点的加工误差见表6 。可见，即使对于同一个零件，当定位方式不同时，零件“表现出”的加工误差也会有所不同。当这样的零件与其他零件装配时，将会引起不同的装配误差。因此，当采用不同的装配顺序进行装配需要调整零件的定位方式时，可能会得到具有不同装配精度的装配体。

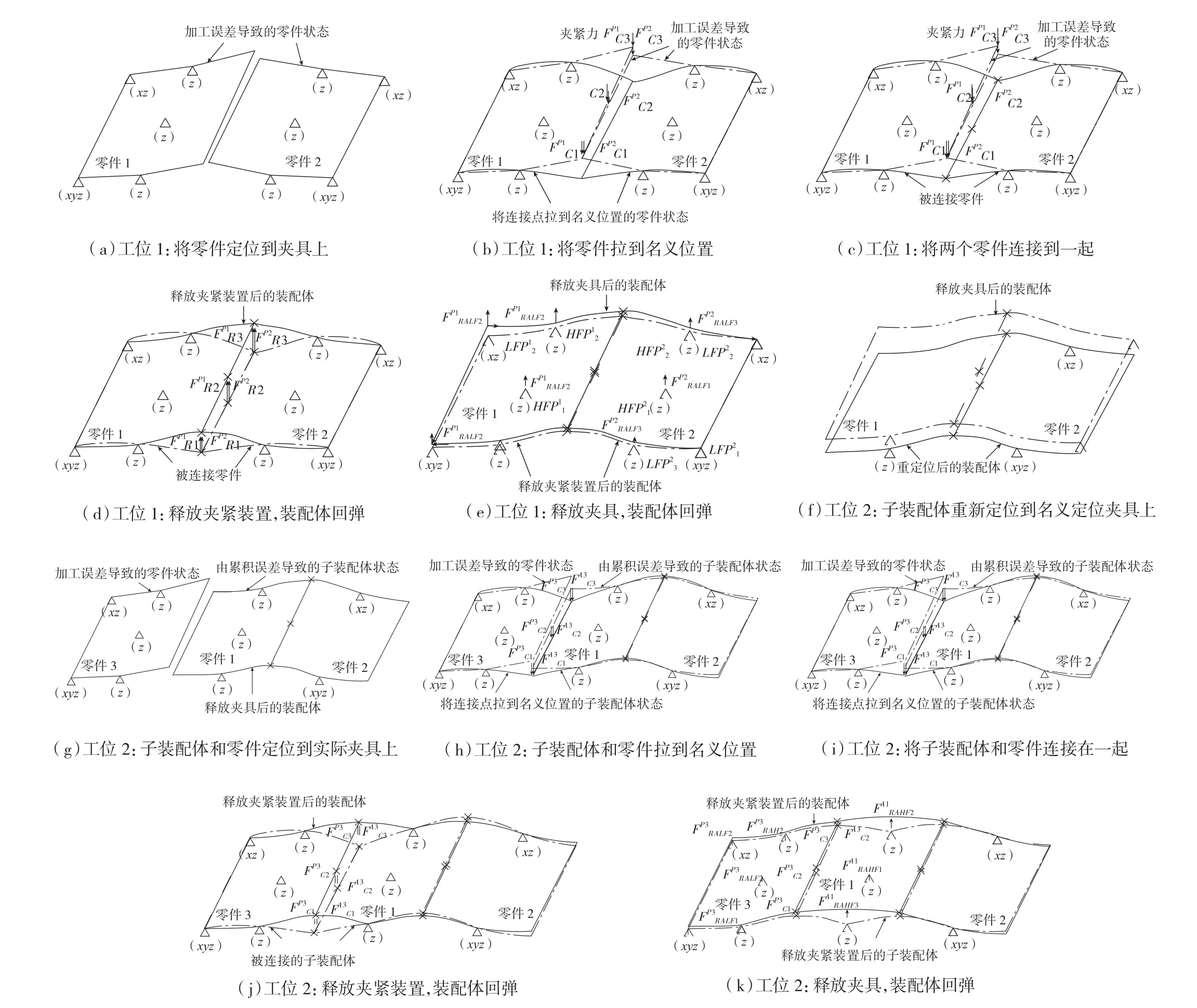
图1 两个装配工位上的3个零件装配过程Fig.1 Assembly process of three parts in two assembly stations

由前文可知，在两种装配方式中，零件1的定位方式有所不同，进而关键点的加工误差也将发生改变。通过前面叙述的方法可以计算得到改变定位方式后的关键点加工误差，进而，采用有限元仿真方法可以预测3-1-2装配方式下的装配体精度。根据表4中4种配对组合方式，采用3-1-2装配方式进行装配得到的测量点装配误差如表7所示。

表5所示为1-2-3装配方式时4种配对组合方式下测量点的装配精度。将表5与表7进行对比，显示在图5～8中，可以发现，对于装配体1来说，无论采用哪种配对组合方式，采用3-1-2装配方式总是比采用1-2-3装配方式时测量点的装配误差大；对于装配体2来说，无论采用哪种配对组合方式，采用3-1-2装配方式总是比采用1-2-3装配方式时测量点的装配误差小。之所以会出现这种现象，原因在于装配体1中的零件1始终采用A号零件，而装配体2中的零件1始终采用B号零件，如表4所示。编号为A的零件1采用1-2-3装配方式时的关键点加工误差和采用3-1-2装配方式对零件1进行重新定位后的关键点加工误差如表8所示。由表8可知，编号为A的零件1在采用3-1-2的装配方式时，关键点的加工误差普遍大于采用1-2-3装配方式下的误差。编号为B的零件1在两种装配方式下的关键点加工误差如表9所示。由表9可知，与编号为A的零件1相反，编号为B的零件1在采用3-1-2装配方式时，关键点的加工误差普遍小于采用1-2-3装配方式下的误差。因此，对于采用编号为A的零件1的装配体1来说，采用1-2-3装配方式，关键点加工误差更小，进而装配精度更高；对于采用编号为B的零件1的装配体2来说 ，采用3-1-2装配方式，关键点加工误差更小，进而装配精度也更高。

表1 有限元仿真材料属性及尺寸

表2 材料属性

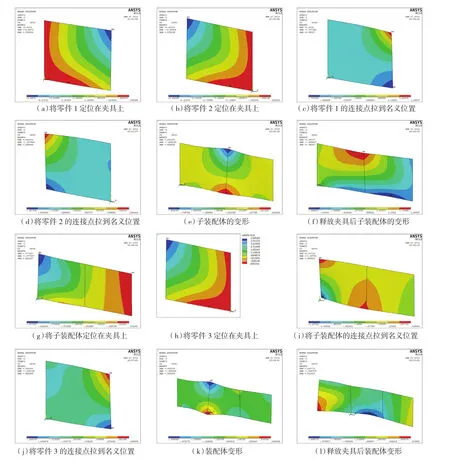
图2 装配体变形误差仿真Fig.2 Simulation of assembly deformation

表3 零件加工误差 mm

表4 零件的配对组合方式

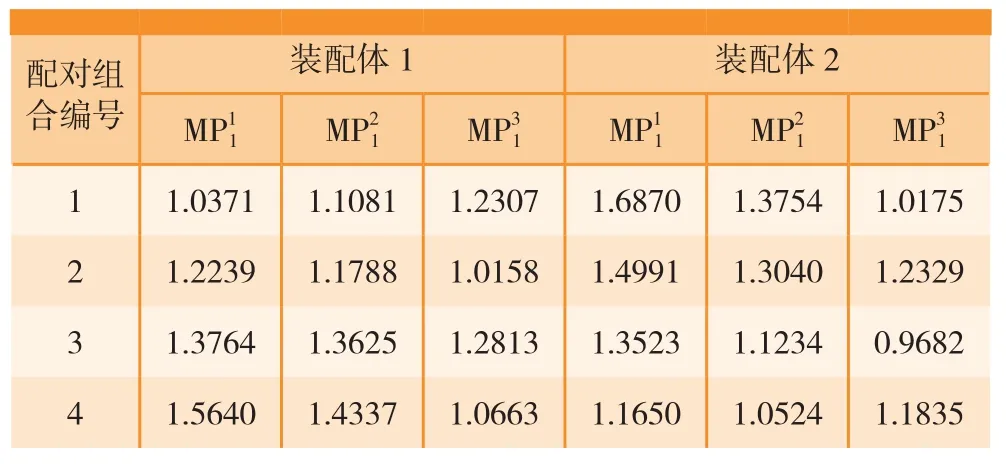
表5 装配精度预测结果 mm

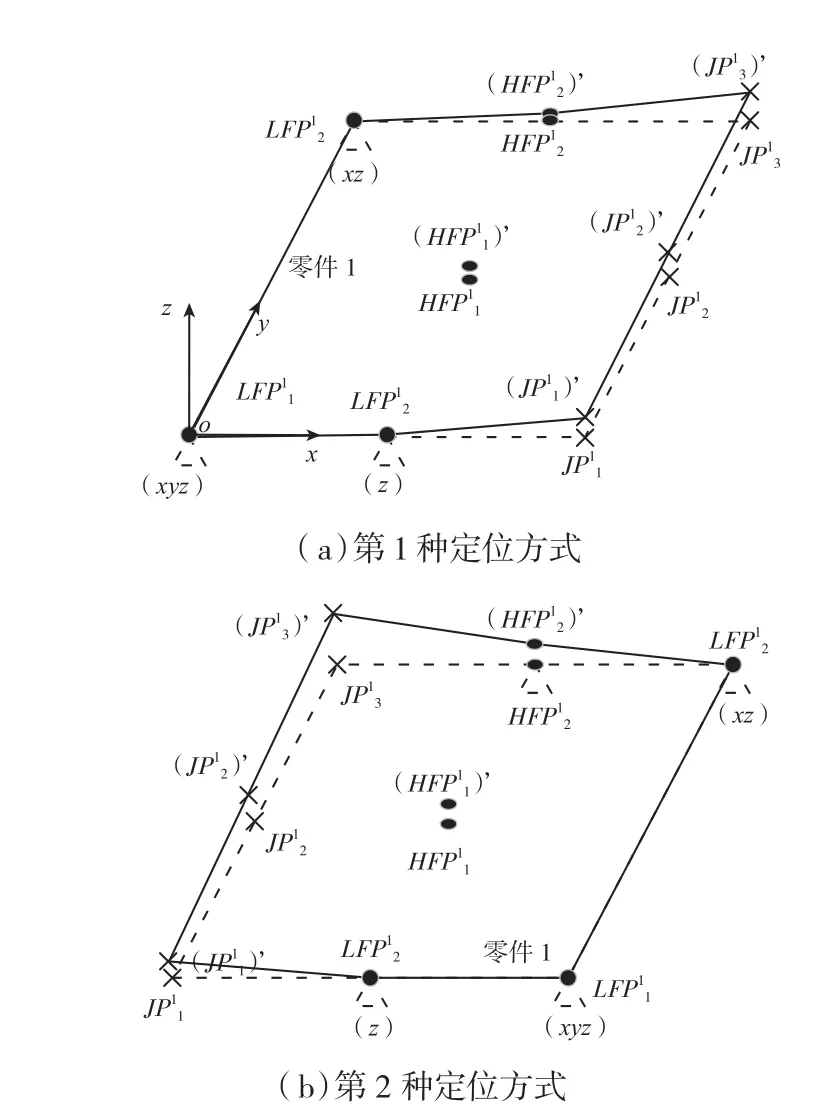
图3 零件1的两种定位方式Fig.3 Two locating methods of part 1

图4 采用第2种定位方式时零件的加工误差Fig.4 Part machining error using the second locating method

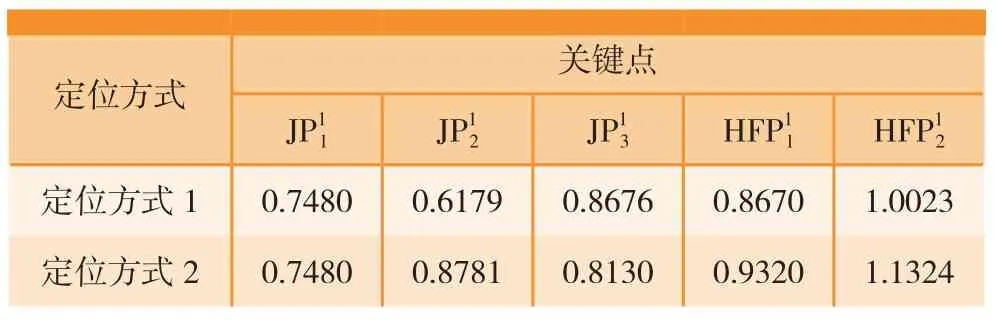
表6 两种定位方式的零件加工误差 mm

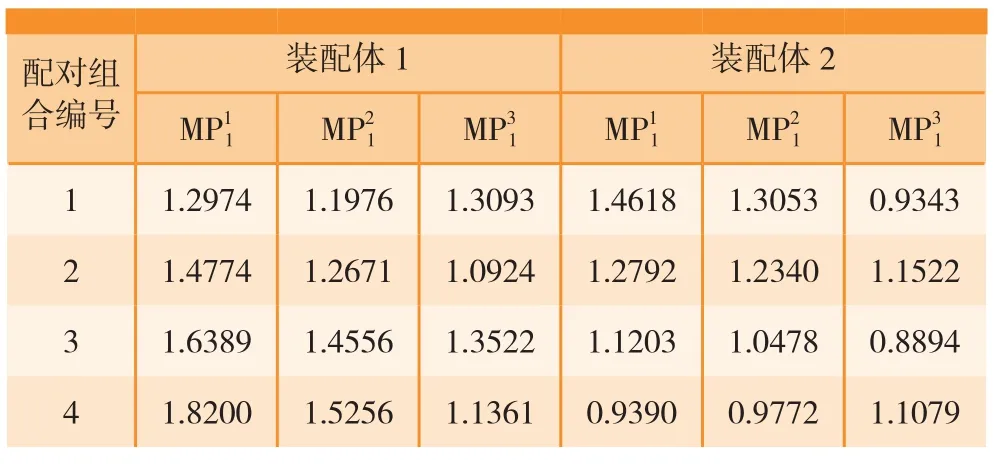
表7 3-1-2装配方式下的装配误差 mm

对于装配顺序可调整的装配体，为了确定最佳装配顺序，可以通过对比改变不同定位方式下的关键点加工误差，来对不同装配顺序下的装配体精度高低进行预判。当然，在有些情况下，可能出现改变定位方式后，部分关键点的加工误差变大，另一部分关键点的加工误差变小，从而无法根据关键点的加工误差进行预判，此时，需要通过有限元仿真方法来预测装配精度。

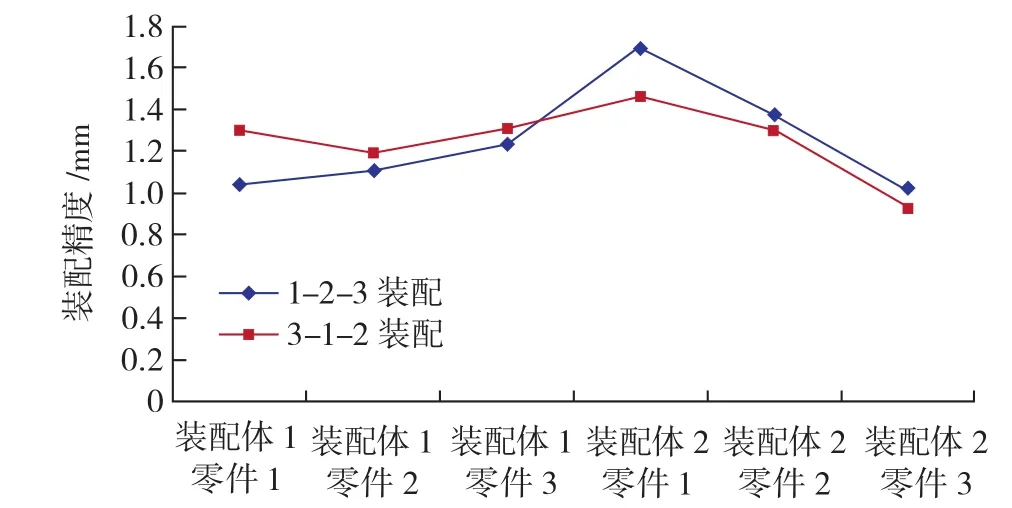
图5 第1种配对组合方式下的两种装配方式得到的装配精度对比Fig.5 Assembly precision comparison in matching mode 1

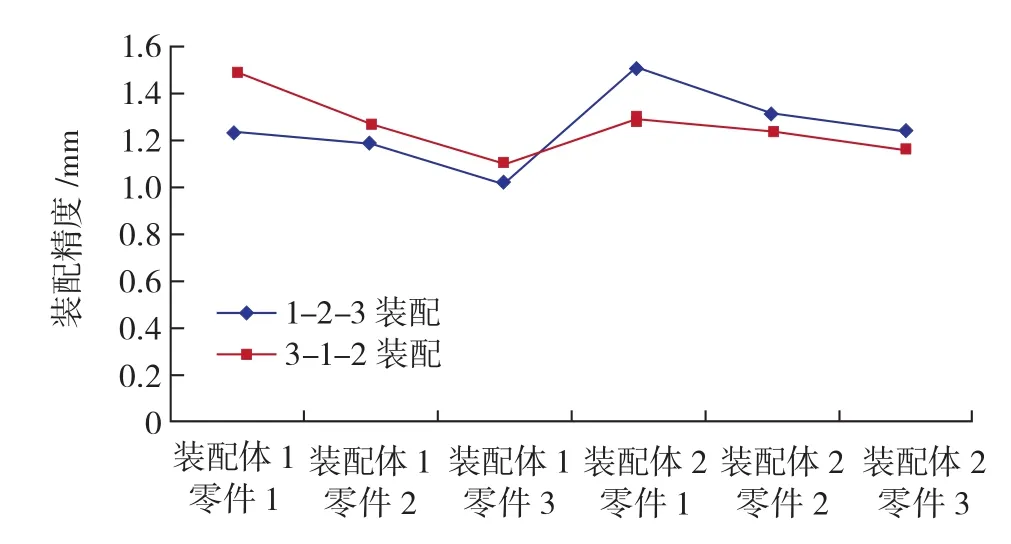
图6 第2种配对组合方式下的两种装配方式得到的装配精度对比Fig.6 Assembly precision comparison in matching mode 2

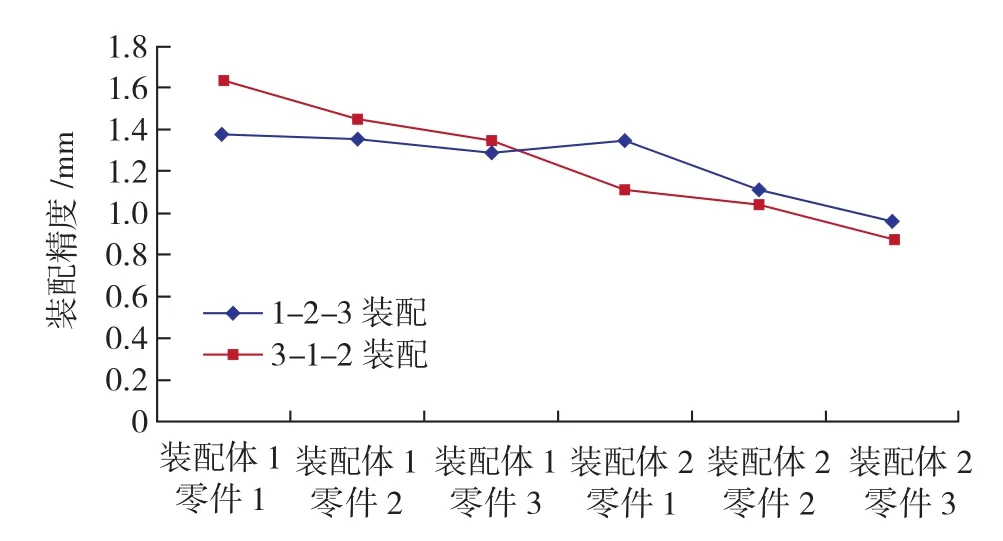
图7 第3种配对组合方式下的两种装配方式得到的装配精度对比Fig.7 Assembly precision comparison in matching mode 3

图8 第4种配对组合方式下的两种装配方式得到的装配精度对比Fig.8 Assembly precision comparison in matching mode 4

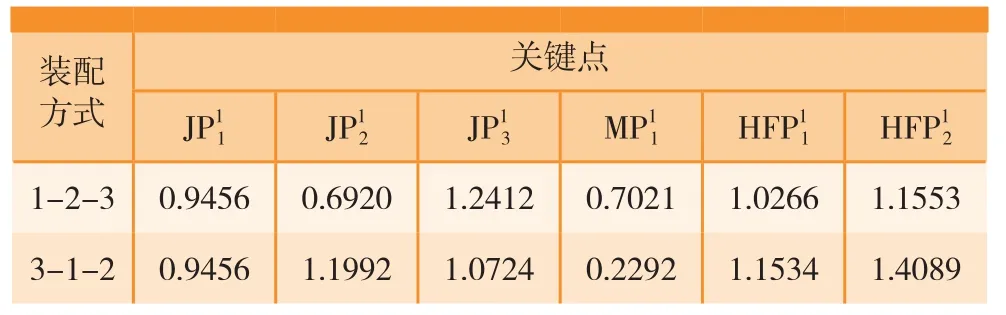
表8 编号为A的零件1关键点加工误差 mm

表9 编号为B的零件1关键点加工误差 mm

4 结论

（1） 针对零件的加工误差特性，优化零件的配对组合形式，将起到误差补偿的作用，从而使装配精度达到最佳。

（2） 对于同样一组零件，调整零件的装配顺序，将对装配精度有所改善。为了适应零件的不同装配顺序，需要改变零件的定位方式，而不同的定位方式影响了零件的误差。

（3） 在复合材料装配的工程实际中，建议先进行零件配对组合方式和装配顺序对装配精度影响的预判，选择最佳的配对组合方式和装配顺序，进而获得最佳装配精度。

参 考 文 献

[1]MALLICK P K. Fiber-reinforced composites: materials,manufacturing, and design[M]. New York: CRC Press Taylor and Frands Group, 2007.

[2]JIN J, SHI J. State Space modeling of sheet metal assembly for dimensional control[J]. Journal of Manufacturing Science & Engineering,1999, 121(4): 756-762.

[3]DING Y, CEGLAREK D, SHI J. Modeling and diagnosis of multistage manufacturing processes: Part I state space model[C]// Japan-USA Symposium of Flexible Automation, Japan, 2000.

[4]LIU S C, HU S J. An offset finite element model and its applications in predicting sheet metal assembly variation[J]. International Journal of Machine Tools & Manufacture, 1995, 35(11): 1545-1557.

[5]LIU S C, HU S J. Variation simulation for deformable sheet metal assemblies using finite element methods[J]. Plos One, 2005, 7(8): e43387.

[6]CAMELIO J, HU S J, CEGLAREK D. Modeling variation propagation of multistation assembly system with compliant parts[J]. Journal of Mechanical Design, 2003, 125: 673-681.

[7]HU J, CAMELIO J. Modeling and control of compliant assembly systems [J]. CIRP Annals-Manufacturing Technology, 2006, 55(1): 19-22.

[8]CAMELIO J A, HU S J, MARIN S P. Compliant assembly variation analysis using component geometric covariance[J]. Journal of Manufacturing Science & Engineering, 2004, 126(2): 355-360.

[9]LIN J, JIN S, ZHENG C, et al. Compliant assembly variation analysis of aeronautical panels using unified substructures with consideration of identical parts[J]. Computer-Aided Design, 2014, 57(57):29-40.

[10]DONG C, KANG L. Deformation and stress of a composite–metal assembly[J]. The International Journal of Advanced Manufacturing Technology, 2012, 61(9): 1035-1042.

[11]CAI W, HU S J, YUAN J X. Deformable sheet metal fixturing:principles, algorithms, and simulations[J]. Journal of Manufacturing Science& Engineering, 1996, 118(3): 318-324.