形状记忆合金驱动器动态驱动性能研究*
(南京航空航天大学机械结构力学与控制国家重点实验室, 南京 210016)
形状记忆合金是一种具有形状记忆效应(Shape Memory Effect,SME)的金属材料,所谓的形状记忆效应是指形状记忆合金(Shape Memory Alloy,SMA)在高温定形后,冷却到低温施加变形,并使它存在残余变形,然后对其加热,当温度超过某个温度后,残余变形即可消失,材料回复到高温时的固有形状,就如同记住了高温下的状态。SMA在相变回复过程中会产生很大的回复应力,因而可将其作为驱动器使用,而且还具有高驱动力、大位移行程、高能量密度和良好的环境适应性等特性,其作为一种智能材料驱动器在实际中特别是航空智能领域得到了广泛的应用(图1)[1]。
针对SMA材料的相变机理,国内外的很多学者开展了广泛的研究。Ko等[2]从分子动力学角度解释了温度和应力诱导马氏体相变的机理。Prasad等[3]通过向Ni49Ti36Hf15合金中加入Ta元素,改善了马氏体的脆弱性和不连续性,提高了形状记忆合金在高温下的工作能力。Yazdandoost等[4]研究了晶格层错能对奥氏体相力学参数的影响,为研究在具有晶格缺陷状况下SMA的属性提供了指导。
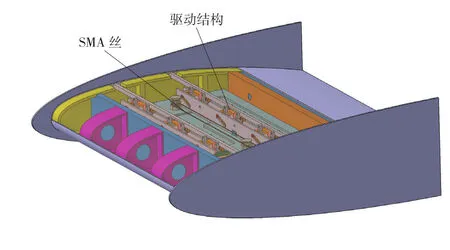
图1 一种基于SMA的变厚度机翼模型Fig.1 A morphing wing with variable sectional thickness actuated by SMA
在SMA相变机理研究的基础上,对其力学本构模型的研究从20世纪80年代初就开始了,Tanaka[5]和Liang[6]根据自由能原理与热力学平衡方程建立了SMA的本构模型;Brinson[7]在Tanaka和Liang模型基础上进行改进,得到了较为成熟的力学本构模型;Kang等[8]提出了在循环载荷作用下,SMA本构模型具有“棘轮效应(Ratchetting)”的现象;Yu等[9]针对“棘轮效应”现象改良了本构模型。Mehrabi等[10]研究了不同加载路径和加载历史下SMA力学性能变化,建立并改良了三维本构模型。
作为驱动器使用的SMA材料,其驱动力、驱动位移等参数与材料的温度、应力、应变、马氏体体积分数等参数具有复杂的非线性关系,这是由于在不同状态下的加热将导致一个复杂的热力学过程,变化的温度、应力等参数在诱发相变时会互相干涉[11]。Zheng等[12]对固定应变状态下回复应力的研究,揭示了不同预拉伸应变下SMA回复应力的区别。Sittner[13]研究了固定应变状态下多次加热冷却循环回复应力和温度的关系,提出了RLOOP算法程序,可以较好地计算固定应变下的回复应力。这些研究阐述了固定应变状态下SMA的热力学属性,并从微观上解释了回复应力产生的机理,但试验过程中加热速度非常缓慢,未考虑到加热速率改变对回复力(驱动力)的影响。
SMA作为驱动器中的驱动元件,经常面临动态加热的工况。本文将通过试验的方法,研究SMA驱动器在实际应用中不同加热速度时的回复力(驱动力)特性,并提出SMA驱动动态性能的数值计算方法,为SMA驱动器驱动力和位移的精确控制提供参考和依据。
SMA静力学本构模型
Tanaka[5]根据自由能原理与热力学平衡方程建立了SMA的本构模型,通过本构方程有效地描述相变过程中SMA的形状记忆效应和伪弹性。能量平衡方程和Clausius-Duhem不等式可表达为:
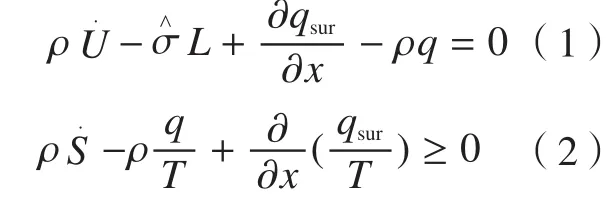
式中,为内能密度;为Cauchy应力;L为速率梯度;qsur为热流;q为热源密度;为嫡密度;ρ为当前构型密度;T为温度;x为材料坐标。
Tanaka通过应变ε、马氏体体积分数ξ和温度T3个状态变量来描述形状记忆合金的状态,即:

根据连续介质力学的热动力学理论,其增量式的本构方程为:
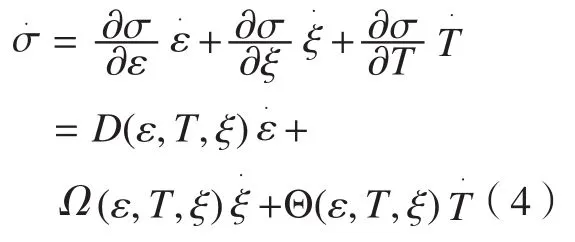
式中,D为形状记忆合金的弹性模量;Ω为相变张量;Θ为形状记忆合金热膨胀系数。
在Tanaka模型研究的基础上,Liang[6]以余弦函数表示马氏体体积分数,根据动力学模型进行了修正,对公式(4)进行积分,得到全量型的本构方程:

式中,σ0、ε0、ξ0、T0为施力前的初始状态。
Tanaka模型与Liang模型虽然形状简单,但在实际应用中存在缺陷。Brinson[7]在Tanaka和Liang模型基础上,提出马氏体体积分数既可以通过应力诱发也可以通过温度诱发,即:

式中,ξT、ξs分别为温度和应力诱发的马氏体体积分数。
Brinson还考虑了弹性模量与马氏体体积分数之间的关系,认为材料的弹性模量与马氏体体积分数为近似线性关系。通常情况下,SMA的弹性模量为材料马氏体体积百分数的函数,于是可将材料的杨氏模量简化为马氏体百分数的线性函数:

式中,DA、DM分别为形状记忆合金完全奥氏体和完全马氏体状态时的弹性模量。
此外,Brinson还引入了形状记忆合金的最大残余应变的概念,并认为材料的相变模量与马氏体体积分数呈线性关系,即:

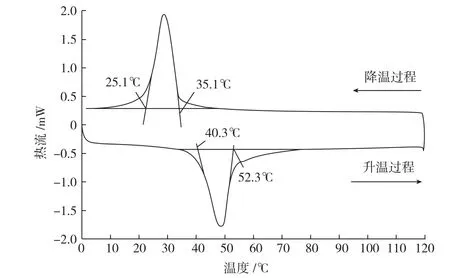
图2 利用DSC测量相变温度Fig.2 Measurements of phase transformation temperature by DSC method
式中,εL为形状记忆合金的最大残余应变。
因此将式(7)和式(8)带入到式(5)中得到修改后的本构方程为:

Tanaka-Liang-Brinson模型的发展经历了一个从一维模型到三维模型,从增量式的表达方式到全量式的表达方式。Brinson 模型的特点是将马氏体体积分数分为温度诱发和应力诱发两部分,有效描述了马氏体的重定向过程,本文以该力学模型作为主要计算依据。
以上模型适用于准静态加热状态下SMA力学特性的计算,考虑到相变过程的复杂性以及非线性特性,SMA加热速率的变化会对其力学性能产生非常大的影响。
SMA力学本构模型的试验测试和分析
基于前述力学本构模型,对直径为1mm的形状记忆合金丝本构模型的各项参数进行了试验测试。首先,利用示差扫描热量计(Differential Scanning Calorimeter,DSC)测试SMA的相变点温度(图2),从图2中可以得到其各个相变温度分别为:奥氏体到马氏体转变起始温度Ms=35.1℃,转变结束温度Mf=25.1℃;马氏体到奥氏体转换起始温度As=40.3℃,转变结束温度Af=52.3℃。
SMA模型其他参数的测定是在图3所示的试验平台上完成的,其中S型力传感器(QL-TSC)右侧通过环氧树脂的绝缘块固定在铝合金型材底座,左侧固定SMA丝试件的一端;SMA丝的另一端固定于滑台上的绝缘块,滑台在步进电机和丝杠的带动下可以精确的左右移动,实现对SMA丝长度的精确控制。
试验中SMA丝初始长度为500mm,采用电流加热的方式使其升温,温度选用了K型热电偶传感器进行测试;PXI数据采集系统完成温度和拉力数据的采集和处理,试验过程中采样频率均设定为100Hz。
考虑到SMA丝刚出厂时的力学性能不稳定,试样在试验前首先通过训练消除其生产过程中的内应力,具体过程为:第1步,将丝加热,使其温度保持在Af以上,然后进行拉伸,拉伸应变为4%,拉伸后保持10s以上,卸载并冷却至Mf温度以下;第2步,在未受力的自由状态下将SMA丝加热到Af以上使其产生相变,然后将其冷却至Mf以下,测试其残余应变;第3步,重复以上步骤,直到残余应变不再变化为止。

图3 SMA性能测试试验平台Fig.3 SMA performance experiment platform
在试验平台上测得SMA本构模型中各参数如表1所示。
为了对SMA的力学特性进行研究,采用表1中试验得到的本构模型的各项参数,对SMA相变过程中温度和回复应力之间的关系进行试验测试和数值计算分析。首先对SMA试件进行预拉伸,拉伸量为6.3%;然后对其缓慢加热至相变结束(80℃),加热温度从40℃开始每次增加2℃,加热速率2℃/min,停留一段时间(至少1min),直到SMA的温度到80℃,测得每次的温度和回复应力数据。
本构模型数值计算中考虑到SMA力学特性受加载历史的影响,采用Kang[8]提出的“棘轮效应”,Brison模型的迭代公式为:

式中,Ti、σi和ζi表示形状记忆合金的当前温度、应力和马氏体体积分数,前一时刻σi-1、Ti-1和ζi-1为计算ζi和σi的初始条件。
试验测试结果和理论计算结果如图4所示, 可以看出SMA的力学本构模型在加热速度很慢(准静态)的情况下,试验测试结果与理论计算结果吻合较好,最大相对误差10.8%,可以根据当前的温度值较好地预测SMA丝的回复应力。
SMA动态力学特性试验和分析
SMA丝试验件保持相同的预拉伸量以及其他试验条件(外部环境温度等)不变的情况下,改变加热速度,加热速率依次取:1.8℃ /s、2.3℃ /s和3.3℃/s,并在每次试验中保持加热速度不变。试验结果如图5所示,相同温度下试件的回复应力差别很大,随着加热速度的提高,相同温度下的回复应力也随之增加。
为进一步研究加热速度对回复应力的影响,在试验过程中改变加热速度。在一次连续加热过程中,以恒定速率将试件加热到50℃(相变进行中),然后切换为另一个加热速度,对回复应力进行测试,共进行了4组试验:第1组,初始加热速率为1.8℃/s,50℃后加热速率切换为2.3℃/s;第2组,初始加热速率为2.3℃/s,50℃后加热速率切换为3.3℃/s;第3组,初始加热速率为3.3℃/s,50℃后加热速率切换为1.8℃/s;第4组,初始加热速率为3.3℃/s,50℃后加热速率切换为2.3℃/s。转变温度设置在50℃是考虑到此时温度在As和Af之间,试样在之前已发生相变并且之后能继续相变。
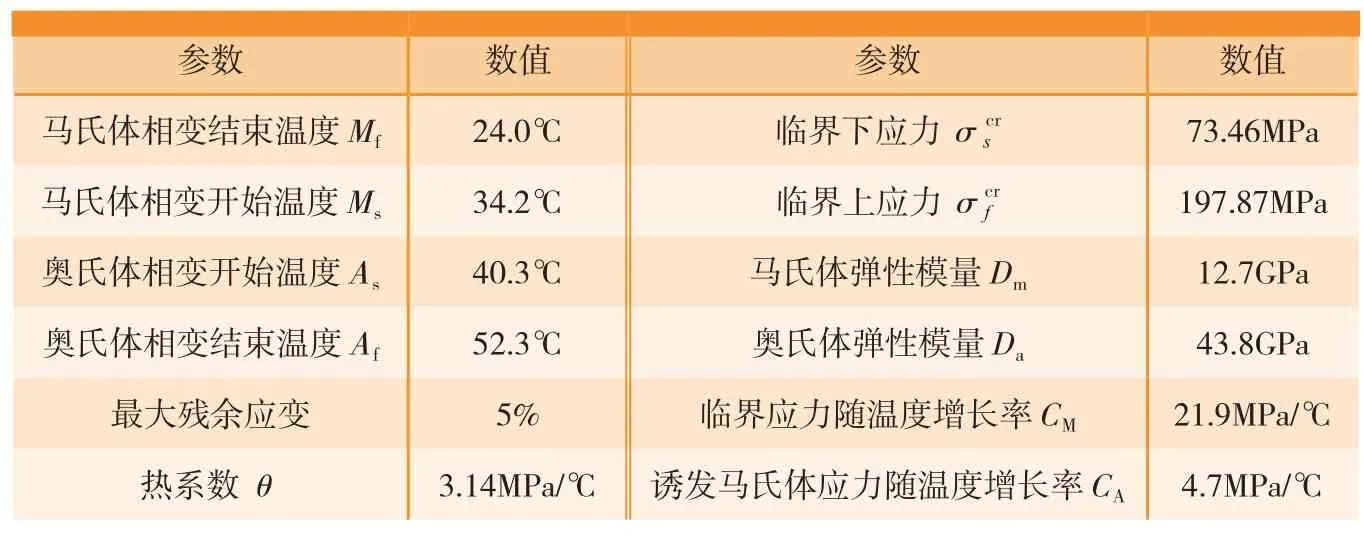
表1 试样属性参数列表
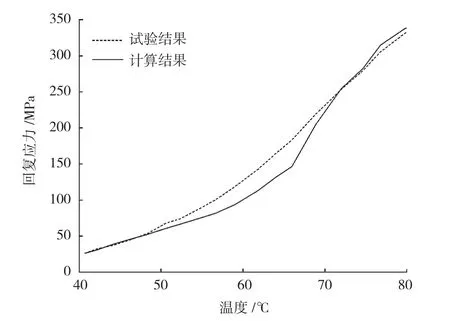
图4 准静态加热实际回复应力和计算数据对比Fig.4 Recovery stress by calculation and experiment in static heating condition

图5 不同加热速率下回复应力温度曲线Fig.5 Recovery stress-temperature curve in different heating conditions
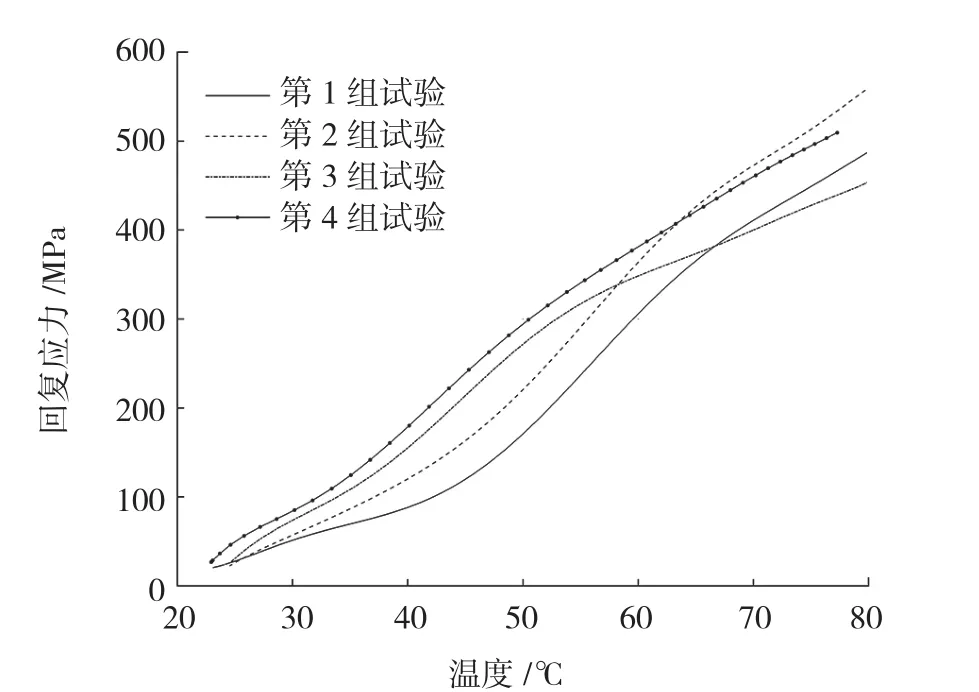
图6 变加热速率下回复应力温度曲线Fig.6 Recovery stress-temperature curve in dynamic heating condition
从图6中可以看出,改变加热速度,SMA丝的回复应力有显著的变化,与本构模型的计算值差别很大,利用已有的本构模型预测其回复应力显然已不可能。
SMA丝作为驱动器时,其驱动力的大小是驱动器的关键参数,从上述的试验结果可知:驱动力(回复应力)的大小与加热速度和温度有关。为了对SMA驱动力进行实时控制和预测,本文提出了一种平均速率插值计算方法,用于解决加热速率变化时SMA回复应力(驱动器的驱动力)的预测问题,即SMA的动态力学性能模型。
以试验测定的不同加热速度下的温度-回复应力曲线为基础,假设加热速率在相邻两条参考线之间切换时,回复应力的增量与平均加热速率的增量成正比。用S(t)表示某时刻的加热速率,表示一段时间内的平均加热速率,平均加热速率为:

用S0、S1分别表示初始加热速率和调整后加热速率;σ0、σ1表示对应参考曲线上的回复应力,则有:

因此:
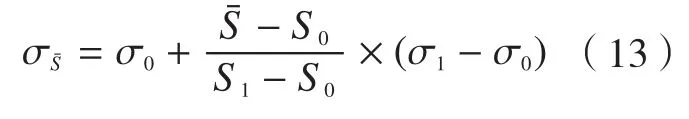
利用上述平均速率插值的计算方法,可以较好地预测加热速率增大或减小情况下的回复应力变化情况,如图7所示。
图7中4组试验计算结果与试验结果的误差如表2所示,其中:平均误差是指误差的平均值;最大相对误差er是指误差的最大值与量程之比;误差的标准差S表示误差的稳定程度。
从试验测试和理论计算的结果可以看出,本文提出的SMA动态力学特性计算和分析方法能够较好预测SMA在不同加热速度和温度下的回复应力,平均预测误差小于13%,最大相对误差小于10%。考虑到SMA本身力学特性具有很强的非线性特性,而且与自身金属成分的含量、制造工艺、热处理方法等都有很大关系,通过试验测试数据,并结合理论模型对其力学特性进行预测和分析是目前较为可行的一种方法,对提高SMA智能驱动器的控制精度有一定的帮助。
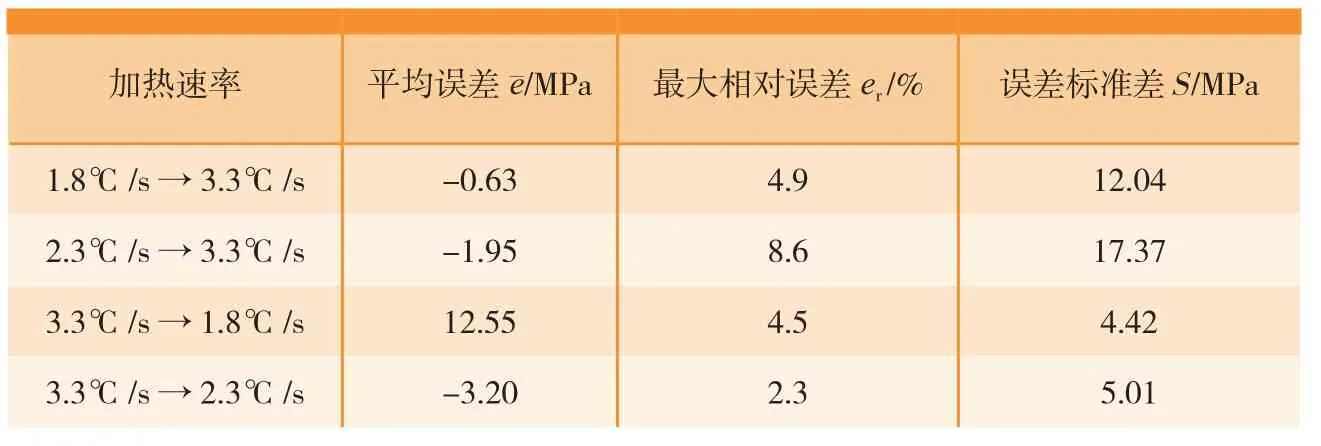
表2 计算数值和试验数据的误差
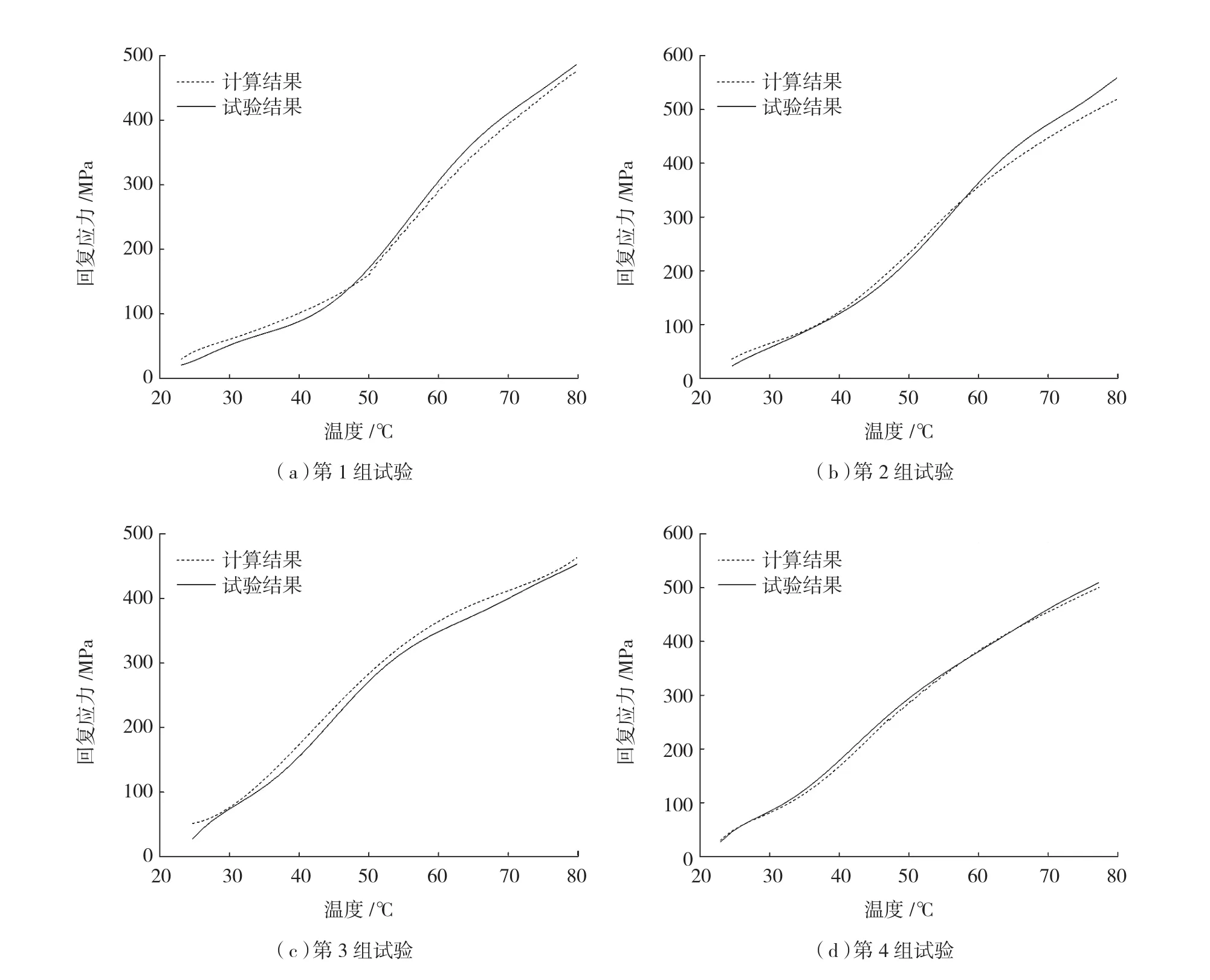
图7 变加热速率下计算回复应力与实际结果比较Fig.7 Recovery stress by calculation and experiment in dynamic heating condition
结论
本文对SMA丝驱动器在不同加热速率下的驱动性能进行了理论和试验分析,提出了不同加热速率下SMA丝驱动力的预测方法,研究表明:
(1)加热速率很慢的准静态加热条件下,基于迭代形式的Brison本构模型可以较好反映SMA材料的力学性能;
(2)恒定加热速率(一定范围内)条件下,随着加热速率的提高,同样温度下SMA丝的回复应力越大;
(3)改变加热速率条件下,利用平均速率插值法可以较好预测加热过程中SMA的回复应力,误差小于10%。
参 考 文 献
[1]王奇, 徐志伟. 形状记忆合金丝驱动器冷却方法理论分析及实验研究[J]. 中国机械工程, 2015, 26(15): 2075-2080 WANG Qi, XU Zhiwei. Theoretical and experimental study of cooling method for SMA wire actuator[J]. China Mechanical Engineering,2015, 26(15): 2075-2080
[2]KO W S, MAISEL S B, GRABOWSKI B, et al. Atomic scale processes of phase transformations in nanocrystalline NiTi shapememory alloys[J]. Acta Materialia, 2017, 123: 90-101.
[3]PRASAD R V S, CHAN H P, KIM S W, et al. Microstructure and phase transformation behavior of a new high temperature NiTiHf-Ta shape memory alloy with excellent formability[J].Journal of Alloys & Compounds, 2016, 697: 55-61.
[4]YAZDANDOOST F, MIRZAEIFAR R.Generalized stacking fault energy and dislocation properties in NiTi shape memory alloys[J]. Journal of Alloys & Compounds, 2017, 709: 72-81.
[5]TANAKA K. A phenomenological description on thermomechanical behavior of shape memory alloys[J]. Pressure Vessel Technology, 1990, 112(2): 158-163.
[6]LIANG C. The constitutive modeling of shape memory alloys[D]. Virginia: Virginia Polytechnic Institute and State University,1990.
[7]BRINSON L C. One-dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with non-constant material functions and redefined martensite internal variable[J]. Intelligent Material Systems and Structures, 1993, 4(4): 229-242.
[8]KANG G Z, KAN Q H, QIAN L M.Ratchetting deformation of super-elastic and shape-memory NiTi alloys[J]. Mechanics of Materials, 2009, 41: 139-153.
[9]YU C, KANG G Z, KAN Q H. A physical mechanism based constitutive model for temperature-dependent transformation ratchetting of NiTi shape memory alloy: One-dimensional model[J]. Mechanics of Materials, 2014, 78: 1-10.
[10]MEHRABI R, SHIRANI M,KADKHODAEI M. Constitutive modeling of cyclic behavior in shape memory alloys[J].International Journal of Mechanical Science,2015, 103: 181-188.
[11]LEONARDO L, ANTONIO C. Shape memory alloy engineering[M]. Waltham: Elsevier Ltd, 2015: 33-76.
[12]ZHENG Y J, SCHROOTEN J.Thermal response of glass fibre/epoxy composites with embedded TiNiCu alloy wires[J]. Materials Science and Engineering, 2002, 335: 157-163.
[13]SITTNER P. Recovery stress generation in shape memory Ti50Ni45Cu5 thin wires[J]. Materials Science and Engineering,2000, 286: 298-311.

