某铜矿露天转地下采矿方法的AHP-FCE法优选

李 斌，王大国，何治良，徐 兵

(西南科技大学环境与资源学院，四川 绵阳 621010)

某铜矿露天转地下采矿方法的AHP-FCE法优选

李 斌，王大国，何治良，徐 兵

(西南科技大学环境与资源学院，四川 绵阳 621010)

采矿方法的优选作为一种典型的多目标决策问题，其结果直接影响到地下采矿作业及相关工程建设，甚至是矿山的最终经济效益。针对某铜矿山即将由露天转向地下的开采现状，为保证其安全高效地可持续发展，从系统工程的角度对初选出的3种采矿方法进行综合评价。应用层次分析法综合考虑6种主要技术经济指标，并采用3标度法较科学合理地确定各指标权重，建立指标权重矩阵。同时，应用模糊综合评价法确定出采矿方法与各指标之间的模糊关系，并建立模糊关系矩阵。最后，将指标权重矩阵与模糊关系矩阵相结合，得到采矿方法关于各指标的综合隶属度。根据综合隶属度的大小，即可对采矿方法的优劣进行排序。排序结果表明，双上山房柱法为最适用于该铜矿山地下开采的采矿方法。

采矿方法；层次分析；3标度法；模糊综合评价

在矿山地下开采活动过程中，采矿方法直接决定着矿山的生产能力、采矿安全、采矿作业及相关工程建设。因此，采矿方法的优选是地下矿山开采设计的一项重点研究内容，其结果的优劣直接影响到矿山能否高效、可持续发展，甚至是关系到矿山企业的最终经济效益[1-2]。尤其是在目前国内矿业经济形势持续疲软[3]的情况下，确定出最优的采矿方法对矿山企业的发展就显得更为重要。

经验类比法作为一种选择采矿方法的传统手段，具有一定的工程指导意义[4-5]。但是，该方法主要依靠工程经验进行决策，存在较大的主观随意性，缺乏足够的科学合理性。鉴于此，近年来国内外大量学者引入了灰色关联分析、层次分析法、神经网络、密切值法等[6-10]]诸多系统工程分析方法应用于采矿方法的决策，并取得了一定的效果。一般而言，采矿方法的优劣通常由矿块生产能力、采切工程量、炸药单耗等多项技术经济指标来进行衡量。因此，从系统工程的角度而言，采矿方法的优选就是一个典型的多目标决策问题。层次分析(AHP)-模糊综合评价(FCE)法作为一种定性和定量分析相结合的方法[11]，能较科学合理地解决系统多目标决策问题。

针对目前四川省凉山彝族自治州某铜矿山即将由露天转向地下的开采现状，为保证其安全高效的可持续发展，本文将应用AHP-FCE法对初选出的几种采矿方法进行优选研究，确定出最适合该矿山的采矿方法，为地下开采设计的相关科学决策提供一定的参考。

1 工程背景

1.1 地质概况

近年来，随着矿产资源的不断开发，目前四川省凉山彝族自治州某铜矿山的露天开采部分已至底部台阶，预计在未来3～5年内该矿山即将转入地下开采。由于井下一系列的采矿作业及相关工程建设都与选择的采矿方法紧密相关，因此为了保证该矿山安全高效地进行地下采矿，必须要解决的一个关键问题就是决策出最优的采矿方法。

根据相关地质资料，该矿山地下开采的主要对象为Ⅲ#矿体，为一缓倾斜至倾斜中厚矿体。该矿体地质特征大体上呈现出走向为NNE-SSW30°左右，倾向为235～270°，倾角为30～50°左右，平均厚度为8.5 m左右，矿岩稳固性在中等稳固以上。

1.2 采矿方法与评价指标确定

根据矿山地质条件及相关开采技术条件，初选出3种可供选择的适用采矿方法：分段法、单上山房柱法和双上山房柱法。

一般而言，评价采矿方法的优劣通常是综合考虑多项技术经济指标来进行衡量。本文根据矿山实际需求及国内外学者在采矿方法优选中常用的评价指标情况，选取矿块生产能力、采矿工效、矿石损失率、矿石贫化率、采切比和炸药单耗这6个指标对上述3种采矿方案进行优选。参照国内外矿山实例，这3种采矿方法的指标值如表1所示。对矿山生产而言，指标C1和C2的数值要求越大越好，而指标C3、C4、C5和C6的数值则要求越小越好。

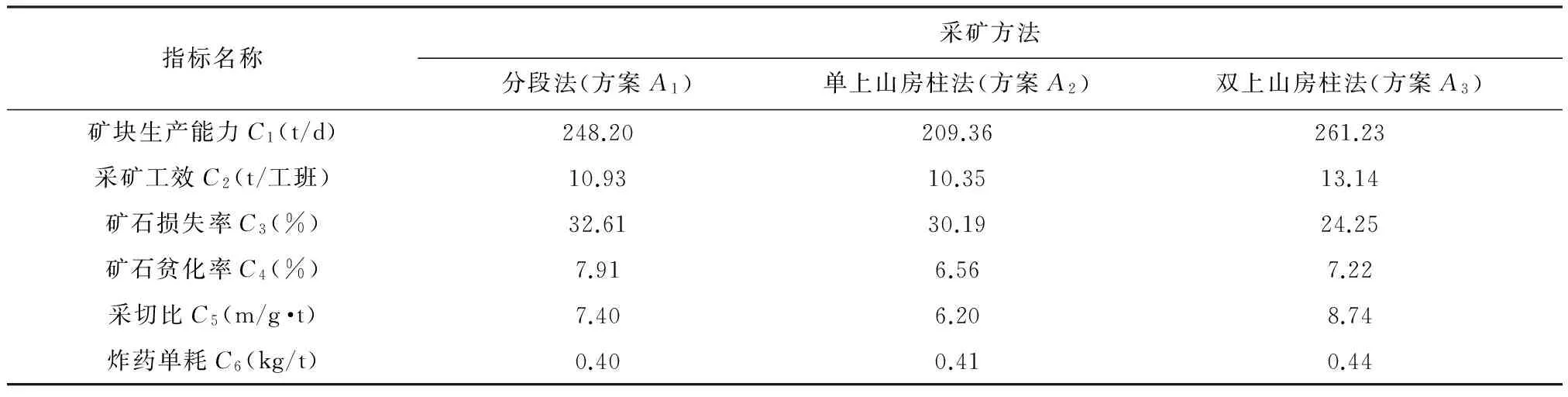
表1 3种采矿方法主要技术经济指标值

2 AHP法确定指标权重

采矿方法中各技术经济指标对矿山生产的重要性一般不同，在进行方案评价之前，首先需要对各指标进行权重评定。层次分析法(AHP)作为一种定量分析与定性分析相结合的系统分析方法[12]，可以在多目标决策问题中较准确地确定出各评价指标的权重，具体的计算步骤主要为：①对指标的重要性进行两两比较，并根据比较结果建立判断矩阵；②计算判断矩阵的特征向量和最大特征根；③判断矩阵的一致性检验，即检验计算出的指标权重是否合理。

下面将采用AHP法对表1中6个评价指标的权重进行确定。

2.1 构造判断矩阵

AHP法确定指标权重的关键在于构造判断矩阵，常用的9标度法在进行指标重要性的两两比较时，通常会由于标准跨度较大而出现不合理的判断，从而导致无法满足一致性检验，需要对判断矩阵进行调整。鉴于此，相关学者通过减小标准跨度，提出了3标度法来进行指标重要性的两两比较，具体方法为：当两个指标Ci、Cj进行比较时，若Ci比Cj重要，以“2”表示；若Ci和Cj同等重要，则用“1”表示；若Ci没有Cj重要，则用“0”表示[13-14]。该方法相对9标度法更易于比较判断，而且建立的判断矩阵能满足一致性检验，计算量少。因此，3标度法在构造判断矩阵中得来越来越广泛的认可和应用[15-18]。

根据矿山的实际情况及相关专家意见，可以对表1中的6个评价指标有一个比较明确的定性认识，即最重要的评价指标是C1，其次是C2、C4和C6同等重要，再其次是C5，最后是C3，而难以定量判断指标间的重要性相差跨度。因此，采用3标度法能较快速方便地构造判断矩阵。通过采用3标度法对这6个评价指标进行两两比较，得到6阶评价矩阵C=(cij)6×6，见式(1)。

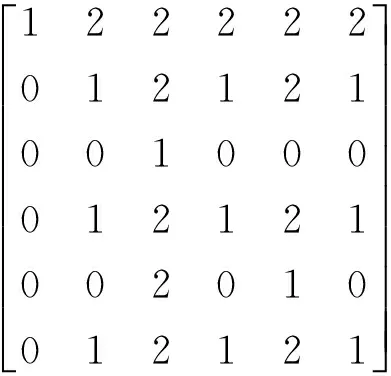
(1)

定义式(2)。

(2)

评价矩阵C按照式(2)计算可得：p1=11，p2=7，p3=1，p4=7，p5=3，p6=7。

可以构造初始判断矩阵B=(bij)6×6，该矩阵中各元素可由式(3)求出。

(3)

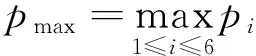
一般情况下，该初始判断矩阵B不具有判断一致性。因此，可以通过式(4)～(6)对矩阵B进行改进，从而使其具有判断一致性。

aij=lgbij(i,j=1,2,…,6)

(4)

(5)

(6)

初始判断矩阵B=(bij)6×6通过式(4)～(6)即可得到最终的判断矩阵B*=(bij*)6×6，且该矩阵具有判断一致性。通过相关计算，得到判断矩阵B*的具体表达式，见式(7)。

(7)

2.2 特征向量和最大特征根计算

根据判断矩阵B*，采用乘积方根法求解其最大特征根λmax和特征向量W。同时，对W做归一化处理，即可得到6个评价指标的权重大小。计算过程主要有以下4个步骤。

1)计算判断矩阵B*中每一行元素的乘积mi，见式(8)。

(8)

2)计算mi的6次方根wi，见式(9)。

(9)

3)将特征向量W=(w1,w2,…,w6)T做归一化处理，见式(10)。

(10)

W*=(w1*,w2*,…,w6*)T即为判断矩阵B*的最大特征根所对应的归一化特征向量。

4)计算判断矩阵B*的最大特征根λmax，见式(11)。

(11)

判断矩阵B*通过按照式(8)～(11)求解得到：W*=(0.504，0.145，0.022，0.145，0.039，0.145)，λmax=6。

2.3 一致性检验

为了分析以上计算得到的特征向量值是否合理，需要对判断矩阵B*进行一致性检验，具体的检验指标为随机一致性比率CR，其数学表达式见式(12)。

(12)

式中，CI为判断矩阵的一致性指标，在本文中针对判断矩阵B*的CIB*=(λmax-6)/(6-1)，由于λmax=6，因此CIB*=0；RI为同阶平均一致性指标，其值由判断矩阵的阶数决定，在本文中判断矩阵B*为6阶矩阵，查询文献[12]相关表可知RIB*=1.249 4。

判断矩阵一致性的准则为CR<1.0，即当CR<1.0时，判断矩阵有可以接受的不一致性；否则，判断矩阵就不合理，需要进行修正，直到通过一致性检验。很明显，针对判断矩阵B*的CR=CIB*/RIB*=0<1.0，说明判断矩阵B*能满足一致性检验，即计算得到的6个指标的权重矩阵(归一化特征向量W*)是合理。同时，也验证了通过3标度法构造的判断矩阵能满足一致性检验这一优点。

因此，矿块生产能力C1、采矿工效C2、矿石损失率C3、矿石贫化率C4、采切比C5和炸药单耗C6的指标权重分别为0.504、0.145、0.022、0.145、0.039和0.145。

3 模糊综合评价

模糊综合评价(FCE)是通过采用模糊关系合成的方式，对受多个因素(评价指标)影响的对象进行较全面的评价。模糊综合评价的过程主要为确定评价集和指标集、确定各评价指标的权重、构造模糊关系矩阵和综合评价。下面通过应用模糊综合评价对初选出的3种采矿方法的优劣进行分析。

3.1 确定评价集和指标集

本文主要是对分段法A1、单上山房柱法A2和双上山房柱法A3这3种采矿方法的优劣进行评判，因此评价集A=[A1,A2,A3]。影响采矿方法的指标为矿块生产能力C1、采矿工效C2、矿石损失率C3、矿石贫化率C4、采切比C5和炸药单耗C6，因此指标集C*=[C1C2C3C4C5C6]。

3.2 构造模糊关系矩阵

根据模糊数学理论，评价集和指标集的模糊关系R(A·C*)可以在直积空间A×C*中表示为式(13)。

(13)

根据表1中3种采矿方法相应的评价指标数值，得到具体的模糊关系矩阵R，见式(14)。

(14)

通过观察表1不难发现，6个评价指标的单位并不相同，而且指标C1和指标C2的数值要求越大越好，而指标C3、指标C4、指标C5和指标C6的数值则要求越小越好。鉴于此，为了使各指标具备可比性，有必要对模糊关系矩阵R进行标准化，具体过程如下所述[12]。

1)针对数值要求越大越好的指标(如指标C1和指标C2)，标准化处理公式见式(15)。

(15)

2)针对数值要求越小越好的指标(如指标C3、指标C4、指标C5和指标C6)，标准化处理公式见式(16)。

(16)

模糊关系矩阵R通过式(15)和式(16)即可得到标准化后的模糊关系矩阵R*，见式(17)。

(17)

3.3 综合评价结果

根据之前得到的6个评价指标的权重矩阵W*和标准化后的模糊关系矩阵R*，采用模糊变换得到模糊决策向量S，即：S=W*R*=(s1，s2，s3)=(0.915，0.862，0.963)。

si表示了方案Ai的综合隶属度，其数值越大则对应的方案就越优。因此，可以按照综合隶属度数值的大小对各方案的优劣进行排序。根据之前计算的模糊决策向量S可知s3>s1>s2，则初选出的3种采矿方法的优劣排序为：方案A3>方案A1>方案A2，即最优方案为双上山房柱法。因此，通过AHP-FCE法分析得出最适用于该铜矿山地下开采的采矿方法为双上山房柱法。

4 结 论

本文通过采用AHP-FCE法，对适用于某铜矿山由露天开采转向地下开采的采矿方法进行了优选研究，并得到以下结论。

1)采用AHP法对评价指标进行权重分配时，采用3标度法构造的判断矩阵能满足一致性检验，计算量小，而且能够保证计算出的指标权重的合理性。因此，建议在应用AHP法分析系统工程问题时采用3标度法取代9标度法。

2)在初选出的3种采矿方案中，最适用于该铜矿山地下开采的采矿方法为双上山房柱法，其次是分段法，单上山房柱法的适用性最差。

3)采矿方法的优选作为一种系统工程问题，采用AHP-FCE法可以有效地解决这类多目标决策问题，可以为方案的最终决策提供一定的参考。鉴于AHP-FCE法的易操作性、实用性和科学性，可以将其推广应用于指导其它矿山工程建设方案(如开拓方法、通风方案、爆破方案等)的优选。

[1] 赵树果, 宋焕虎, 宋卫东. 基于粗糙模糊集理论的采矿方法优化研究[J]. 金属矿山, 2015(5): 48-51.

[2] 姚囡, 叶义成, 王其虎, 等. 基于统计模糊权重和模糊区间评价的采矿方法优选模型[J]. 中国矿业, 2014, 23(9): 112-117.

[3] 姚华军, 刘伯恩, 陈俊楠, 等. 当前矿业经济形式及未来展望[J]. 中国国土资源经济, 2014(1): 4-7.

[4] 王新民, 秦健春, 张钦礼, 等. 基于AHP-TOPSIS评价模型的姑山驻留矿采矿方法优选[J]. 中南大学学报: 自然科学版, 2013, 44(3): 1131-1137.

[5] 丁福龙, 丁德馨, 叶勇军. 某铀矿山独立矿区Ⅲ#矿体采矿方法选择[J]. 南华大学学报: 自然科学版, 2010, 24(2): 19-23.

[6] 陈东, 周传波, 李超人, 等. 基于灰关联与层次分析的地下开采采矿方法优选[J]. 黄金, 2015, 36(8): 28-31.

[7] ATAEI M, SHAHSAVANY H, MIKAEIL R. Monte Carlo Analytic Hierarchy Process (MAHP) approach to selecting of optimum mining method [J]. International Journal of Mining Science and Technology, 2013, 23(4): 573-578.

[8] KARIMNIA H, BAGLOO H. Optimum mining method selecting using fuzzy analytical hierarchy process-Qapiliq salt mine, Iran [J]. International Journal of Mining Science and Technology, 2015, 25(2): 225-230.

[9] 陈建宏, 刘浪, 周智勇, 等. 基于主成分分析与神经网络的采矿方法优选[J]. 中南大学学报: 自然科学版, 2010, 41(5): 1967-1972.

[10] 李明, 郑怀昌, 赵勇, 等. 多目标决策密切值法在侯庄矿采矿方法优选中的应用[J]. 矿冶工程, 2010, 30(1): 5-8.

[11] 张丽, 柏萍, 汪忠雨, 等. 基于层次分析与模糊综合评价的事故应急预案评估[J]. 中国安全生产科学技术, 2015, 11(9): 126-131.

[12] 叶义成, 柯丽华, 黄德育. 系统综合评价技术及其应用[M]. 北京: 冶金工业出版社, 2006.

[13] 郭秀英. 预测决策的理论与方法[M]. 北京: 化学工业出版社, 2010.

[14] 左军. 层次分析法中判断矩阵的间接给出法[J]. 系统工程, 1988, 10(6): 56-63.

[15] ZHOU W, XU Z. Asymmetric hesitant fuzzy sigmoid preference relations in the analytic hierarchy process [J]. Information Sciences, 2016, 358-359: 191-207.

[16] WANG Q, WANG H, QI Z. An application of nonlinear fuzzy analytic hierarchy process in safety evaluation of coal mine [J]. Safety Science, 2016, 86: 78-87.

[17] 王硕, 徐凌, 杜静, 等. 3标度层次分析法下盘锦人口预测方法的优选[J]. 数学的实践和认识, 2012, 42(16): 158-167.

[18] 丁丽宏. 基于改进的灰关联分析和层次分析法的边坡稳定性研究[J]. 岩土力学, 2011, 32(11): 3437-3441.

Optimization of mining methods in a certain copper mine based on the AHP-FCE method

LI Bin, WANG Daguo, HE Zhiliang, XU Bing

(School of Environment and Resource, Southwest University of Science and Technology, Mianyang 621010, China)

The optimization of mining methods is a kind of typical multi-objective decision problems. Its results directly effect mining operations and related engineering construction, even the economic benefits. In order to guarantee the sustainable development of a certain copper mine, transferring from open pit into underground mining, a comprehensive evaluation of three primary selected mining methods was carried out from the view of system engineering. Six indicators were overall considered by analytic hierarchy process, and their weight were defined scientifically and reasonably to establish index weight matrix. Simultaneously, a fuzzy relation matrix, indicating the fuzzy relationship between mining methods and indicators, was also established by applying fuzzy comprehensive evaluation method. Finally, comprehensive feudatory degrees of the three mining methods could be obtained by combine the index weight matrix and fuzzy relation matrix. Then, the mining methods can be ranked according to the value of comprehensive feudatory degrees. The ranking results show that double room and pillar method is the most suitable for underground mining of the copper mine.

mining method; analytic hierarchy process (AHP); three sign degree; fuzzy comprehensive evaluation (FCE)

2016-12-28

四川省教育厅科研项目资助(编辑：16CZ0013、15ZB0124)；绵阳市科技计划项目资助(编号：14S-02-6)；西南科技大学博士研究基金项目资助(编号：15zx7134)

李斌(1988-)，男，湖北钟祥人，讲师，博士，主要从事岩石力学及采矿方法与工艺方面的研究，E-mail:li19880506@126.com。

TD862.1

A

1004-4051(2017)05-0117-05