不均匀胶层对CFRP板加固梁的界面应力影响*

杜运兴，侯春旭，周芬

(湖南大学 土木工程学院,湖南 长沙 410082)



不均匀胶层对CFRP板加固梁的界面应力影响*

杜运兴†，侯春旭，周芬

(湖南大学 土木工程学院,湖南 长沙 410082)

采用数值试验研究了CFRP板加固钢筋混凝土梁中不均匀胶层的应力及加固界面应力．被加固梁界面上设置缺口改变胶层的局部厚度，根据缺口的深度、宽度、位置建立6种分析工况.研究表明，缺口距离CFRP板端部较近时，界面峰值应力会高于无缺口工况，缺口远离CFRP板端部位置时，峰值界面应力几乎不受影响；缺口距离CFRP板端部为CFRP板长的0.83%和1.25%时，峰值界面剪应力和正应力分别达到最大值；当缺口的长度或深度增大时，峰值界面剪应力和界面正应力均增大，界面应力对于缺口深度更敏感；在远离CFRP板端部区域，胶层中的应力沿其厚度方向均匀分布；当缺口出现在CFRP板端部附近时，CFRP板端部胶层中的应力沿厚度方向变化更大且应力在缺口区域内分布更加不均匀.

CFRP；缺口；有限元分析；界面应力；应力分布

近年来，FRP加固技术在土木工程领域得到了广泛的应用和发展.该技术的主要优势是结构自重增加小、施工简单.研究表明[1-2]，剥离破坏是FRP加固混凝土梁的一种重要的破坏模式.这种破坏往往发生在混凝土和胶层的界面或混凝土梁底部保护层内[3]，由于被加固构件的界面存在较大的界面应力，致使界面或界面附近混凝土首先出现破坏，此时FRP材料的抗拉强度并未得到充分发挥，大大降低了FRP的加固效果.因此，这一破坏引起了国内外学者的广泛重视.

在界面应力的研究中通常忽略胶层的厚度.例如：T. Stratford等[4]采用差分法获得了黏板加固梁的界面应力，该方法虽可以考虑黏结缺陷对于加固效果的敏感程度，但仍未考虑胶层的厚度.Lu等[5]、尚守平等[6]分别采用有限元法对剥离破坏和界面黏结性能进行研究，采用界面单元模拟胶层，采用界面单元的失效模拟剥离破坏，但是界面单元同样没有厚度.Teng等[7]及张术宽[8]在研究FRP端部剥离破坏的界面应力及相应参数时考虑了模型胶层的厚度，研究获得了稳定应力值应采用的单元尺寸及胶层中应力的分布规律．Teng等[7]和张术宽[8]的有限元模型只模拟了均匀胶层的情况，因此这类方法并不能研究胶层几何尺寸对于界面应力的影响.根据Smith[9]，Tounsi[10]，Rabinovich[11]和Shen[12]等的理论分析及参数研究，胶层厚度是影响界面应力的一个重要因素.因而，在研究界面应力时不可忽视胶层的厚度，对胶层独立建模是研究界面应力的关键.

FRP加固钢筋混凝土梁时，要求梁的加固面平整.实际工程中在粘贴FRP前需要对加固面进行处理，一方面需要去除梁的粉刷层，另一方面需要凿毛加固面.这2种情况均会造成加固面的不平整.为了达到黏结表面平整度的要求，实际工程中通常采用胶层进行找平，这就导致了胶层厚度沿梁长度方向不均匀.

本文采用数值仿真的方法研究不均匀胶层对界面应力、胶层应力的影响.在梁的加固面设置缺口，缺口内填筑胶体，通过改变缺口的位置、深度、长度模拟不均匀胶层的变化.将缺口内的胶体和黏结层的胶体均进行有限单元划分，从而研究该位置界面应力和胶层应力.

1 有限元模型

1.1 整体有限元模型的建立

采用有限元软件MSC.MARC建立CFRP板加固的简支梁计算模型.简支梁计算跨度为3 000 mm，CFRP板的长度为2 400 mm，简支梁承受均布荷载为50 kN/m，简支梁、胶层和CFRP板的几何特征和材料参数见表1.将计算模型简化为平面应力问题.梁、胶层和CFRP板均采用四节点四边形平面应力单元，并选用缩减积分单元，以便更好地模拟剪切变形及弯曲变形，计算模型如图1所示.

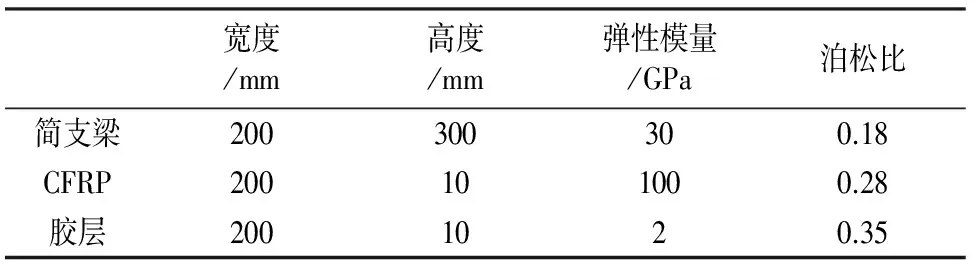
表1 加固梁各组成部分几何特征和材料特征Tab.1 Geometry and material properties of different segments of CFRP plate strengthened beam

图1 CFRP加固简支梁整体有限元模型Fig.1 Global finite element model of simply supported beam strengthened by CFRP plate

1.2 局部有限元模型的建立

为了对CFRP板端部的界面应力进行更准确的分析，同时兼顾计算效率，本文采用MSC.MARC中的global-local的功能[11]，先将整体模型进行运算，然后从整体模型中分离出CFRP板端部的局部有限元模型，对局部模型的网格进行加密处理，缩小其单元尺寸.利用整体模型的计算结果文件，将整体模型中相应位置的应力和位移等已知量作为局部模型中的边界条件，施加在局部模型相对应的位置，然后对局部模型进行运算.局部模型如图2所示.

图2 CFRP板加固简支梁局部有限元模型Fig.2 Local finite element model of simply supported beam strengthened by CFRP plate

1.3 梁底部缺口的布置

建立梁底部有一个凹型缺口的计算模型，缺口内部采用胶层进行找平，该位置胶的材料参数与胶层的参数相同.通过改变缺口的长度、深度和缺口距离CFRP板端部的位置这三个因素研究界面应力和胶层中应力分布的影响.具体的工况设置见表2，表2中的相对缺口长度为缺口长度与CFRP板长度的比值，相对缺口深度为缺口深度与梁高度的比值，缺口到CFRP板端部的相对距离为缺口到CFRP板端部的距离与CFRP板长度的比值.

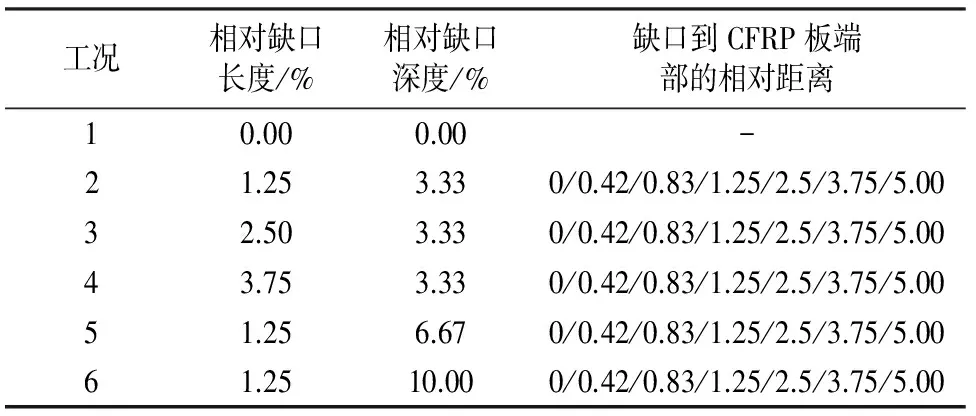
表2 有限元分析工况设置Tab.2 Load cases of finite element analysis

2 计算结果及分析讨论

2.1 缺口位置对界面应力的影响

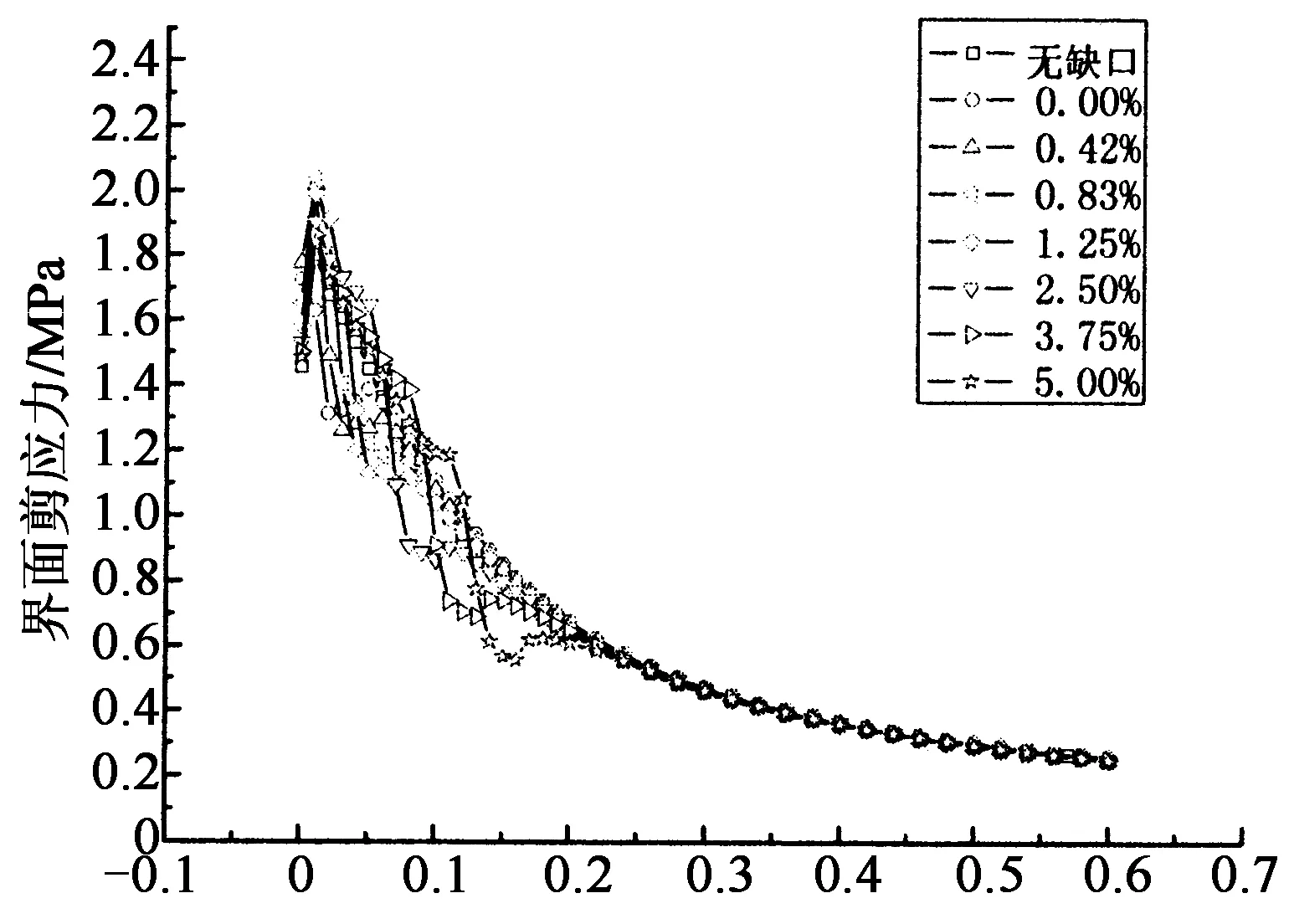
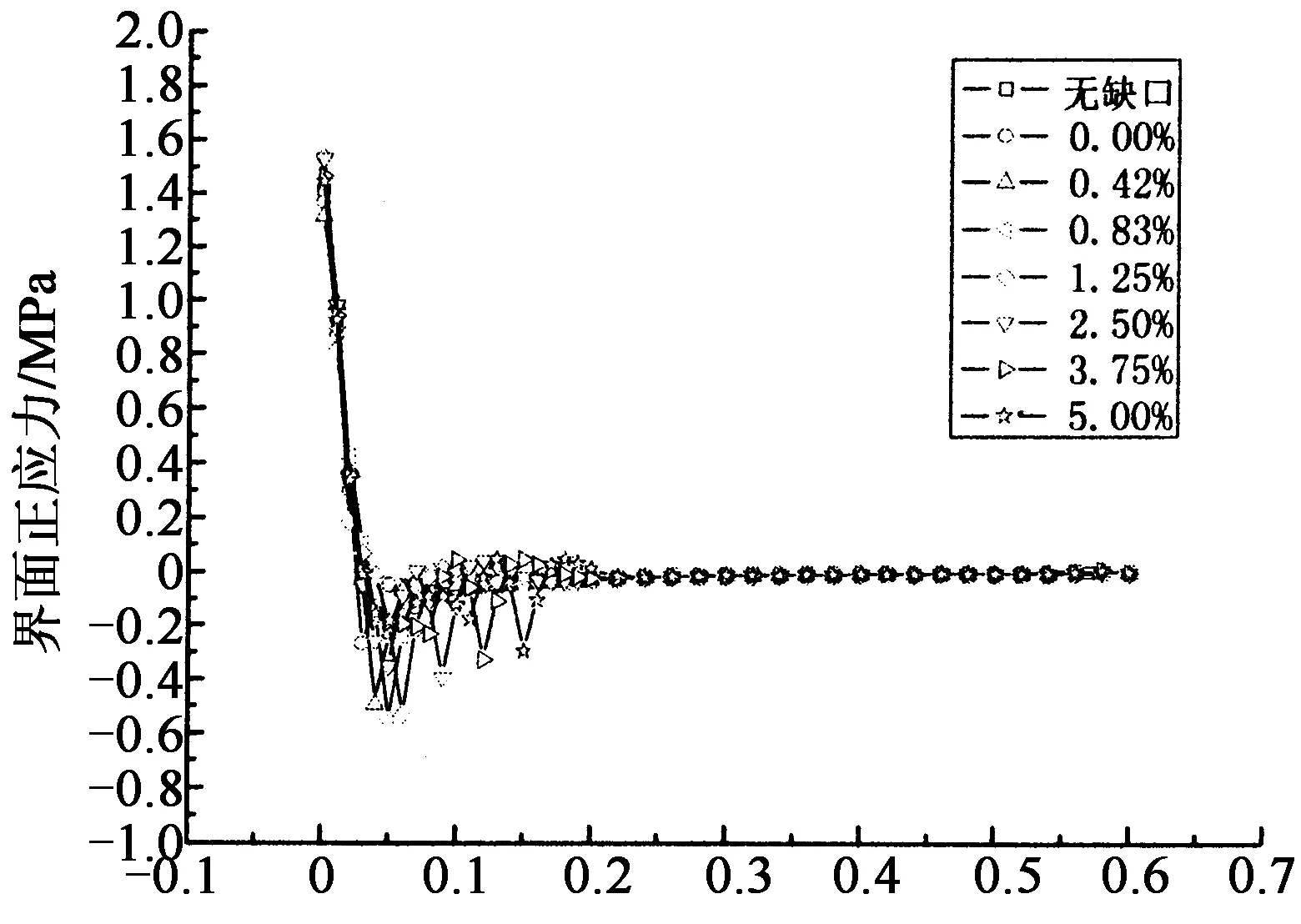
根据工况2的计算结果，缺口的位置对于界面应力的影响如图3(a)(b)所示.由图3(a)可知，界面剪应力曲线开始较低，在到CFRP板端部的距离为CFRP板长的0.42%处达到了最大值；由图3(b)可知，界面正应力曲线在CFRP板端部达到最大值.当缺口位于CFRP板端部时，峰值界面剪应力和界面正应力均比无缺口的工况有一定程度的降低.当缺口不在CFRP板端部位置时，峰值界面应力相比无缺口工况的界面应力均有不同程度的提高.其中峰值界面剪应力在缺口位于CFRP板长的0.83%处时达到了最大值，峰值界面正应力在缺口位于CFRP板长的1.25%处时达到了最大值.峰值界面应力随着距CFRP板端部的距离增大而降低，当缺口位于CFRP板长的5.00%时，峰值界面应力相比无缺口工况的峰值界面应力提高幅度很小.造成这一现象的原因是在缺口位置胶层厚度突变，在缺口附近出现应力改变，而应力改变只对缺口周围区域的应力分布有影响，所以缺口出现的位置离CFRP板端部越远，其对于峰值界面应力的影响越小.

由图3(a)(b)的界面应力曲线可以看出，相比于无缺口情况的界面应力曲线，在缺口周围，界面应力曲线会出现明显的波动，而在远离缺口的区域，两者基本吻合.对于其他工况，缺口出现的位置对于界面应力曲线的影响可得到相似结论.

到CFRP端部的距离/m (a) 界面剪应力

到CFRP端部的距离/m (b) 界面正应力图3 缺口在不同位置处的界面应力曲线Fig.3 Interfacial stress curves with notches in different locations

2.2 缺口长度和高度对界面应力的影响

由2.1节可知，峰值界面剪应力和正应力分别在缺口位于CFRP板长的0.83%和1.25%处达到了最大值.综合比较0.83%和1.25%时的界面剪应力和正应力值，选取当缺口位于CFRP板长的1.25%处的情况计算各个工况的峰值界面应力，结果汇总于表3.

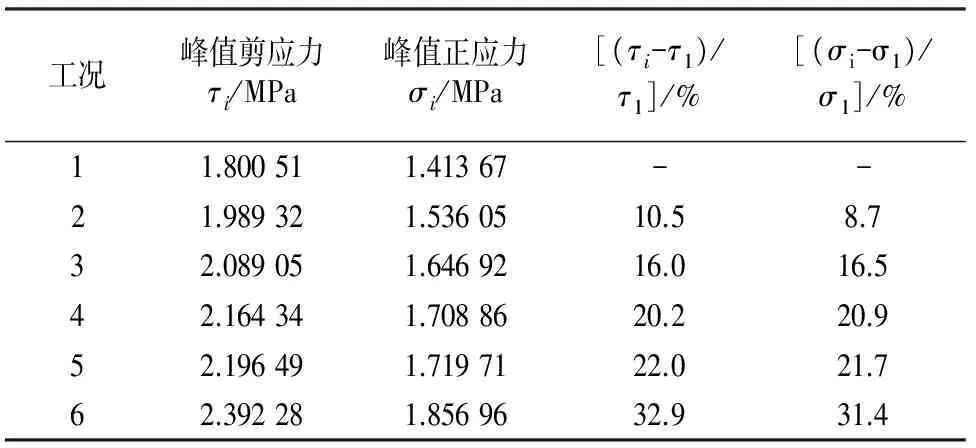
表3 各个工况峰值界面应力的最大值Tab.3 Maximum values of peak interfacial stresses of different load cases

注：表中i为各工况的编号．

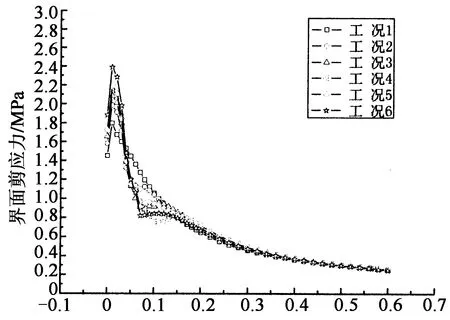
图4(a)(b)分别综合反映了缺口长度和高度对界面剪应力、正应力的影响.分析表明，峰值界面剪应力、正应力均随着缺口长度的增加而增加，其相应的提高程度见表3.由图4(a)可知，界面剪应力的曲线在CFRP板端部附近迅速达到了最大值，然后出现了下降段.在缺口周围的区域，有缺口情况的界面剪应力的下降段斜率更大，应力降低速度更快.在远离缺口周围的区域，两者的下降段斜率基本一致.不同缺口长度的界面剪应力曲线下降段斜率基本相同，说明缺口长度变化对于下降段的斜率没有影响.由图4(b)可知，界面正应力在CFRP板端部达到最大值，然后开始下降，最终趋近于零.无论是否有缺口的存在，界面正应力曲线的下降段斜率基本相同.缺口长度的变化只影响界面应力的数值大小，并不改变界面应力分布.

对于不同缺口深度，峰值界面剪应力、正应力均随着缺口深度的增加而增加，其相应的提高程度见表3.不同高度时的界面应力曲线与不同缺口长度情况相似，界面剪应力曲线在CFRP板端部附近迅速达到最大值，然后就出现了一个下降段；界面正应力在CFRP板端部达到最大值，然后开始下降，最终趋近于零.缺口深度同样对界面应力曲线下降段斜率没有影响.缺口深度的变化同样只影响界面应力的数值大小并不改变界面应力分布.

由表3可知，相比于无缺口情况的界面应力，有缺口情况峰值界面剪应力的提高幅度分别为:32.9%(工况6)>22.0%(工况5)>20.2%(工况4)>16.0%(工况3)>10.5%(工况2).可以看出，界面应力对于缺口深度的变化比对缺口长度的变化更加敏感.缺口深度对于界面应力的影响明显大于缺口长度的影响.缺口周围的应力集中情况也与缺口的形状有关，当缺口面积相同时，缺口深度与长度的比值越接近1(工况6)，界面应力集中程度越高，峰值界面应力越大.

到CFRP层端部的距离/m (a)界面剪应力

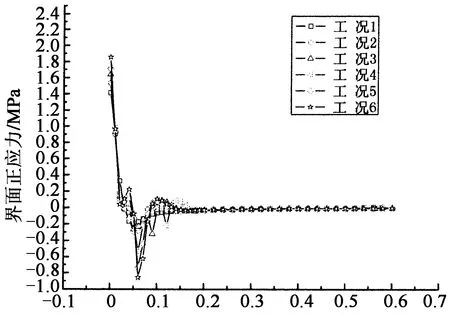
到CFRP层端部的距离/m (b) 界面正应力图4 不同工况的界面应力对比Fig.4 Comparison of interfacial stresses under different load cases

由2.1节可知，当缺口存在时，界面应力曲线会在缺口周围出现一个明显的波动，当缺口位于CFRP板长的1.25%处时，各个工况界面应力波动数值见表4.由表4可以看出，随着缺口长度的增加，界面剪应力波动幅度增大，正应力波动幅度减小；随着缺口深度的增加，界面剪应力和正应力波动幅度均增大.综合剪应力和正应力的情况，缺口深度对缺口周围应力集中程度和界面应力分布的影响更大.

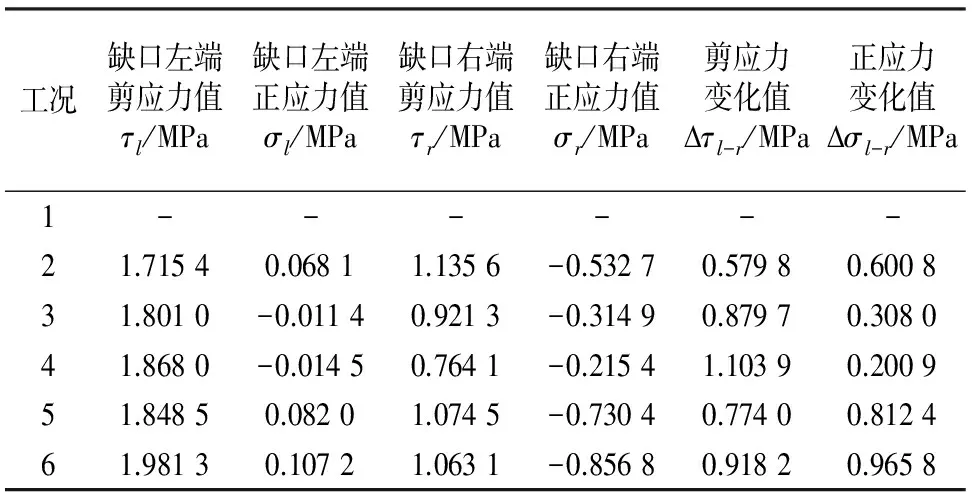
表4 各个工况缺口处界面应力的波动值Tab.4 Fluctuation values of interfacial stresses for different load cases around notch

2.3 胶层中的应力分布

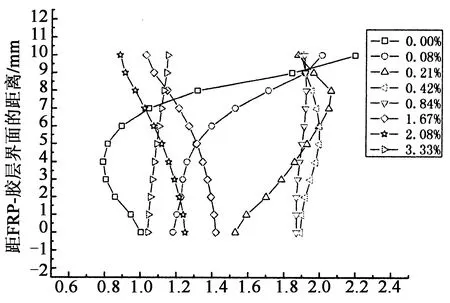
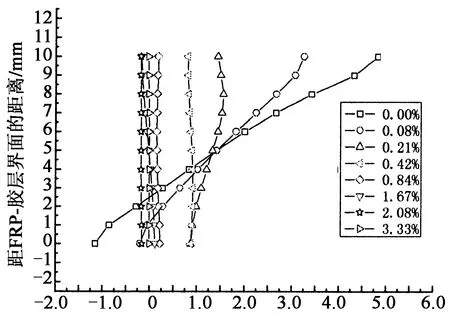
在本小节中，对CFRP板端附近胶层中的应力分布进行了研究.结果如图5—图7所示，其中纵坐标为距离CFRP板-胶层界面的竖直距离，横坐标为相应的应力值，各条曲线表示距离CFRP板端部不同位置处的应力分布，分别为0 mm(0%)，2 mm(0.08%)，5 mm(0.21%)，10 mm (0.42%)，20 mm(0.84%)，30 mm(1.25%)，40 mm (1.67%)，50 mm(2.08%)，60 mm(2.50%)或80 mm(3.33%).其中，括号里的值为各个位置到CFRP板端部的距离与CFRP板长度的比值.

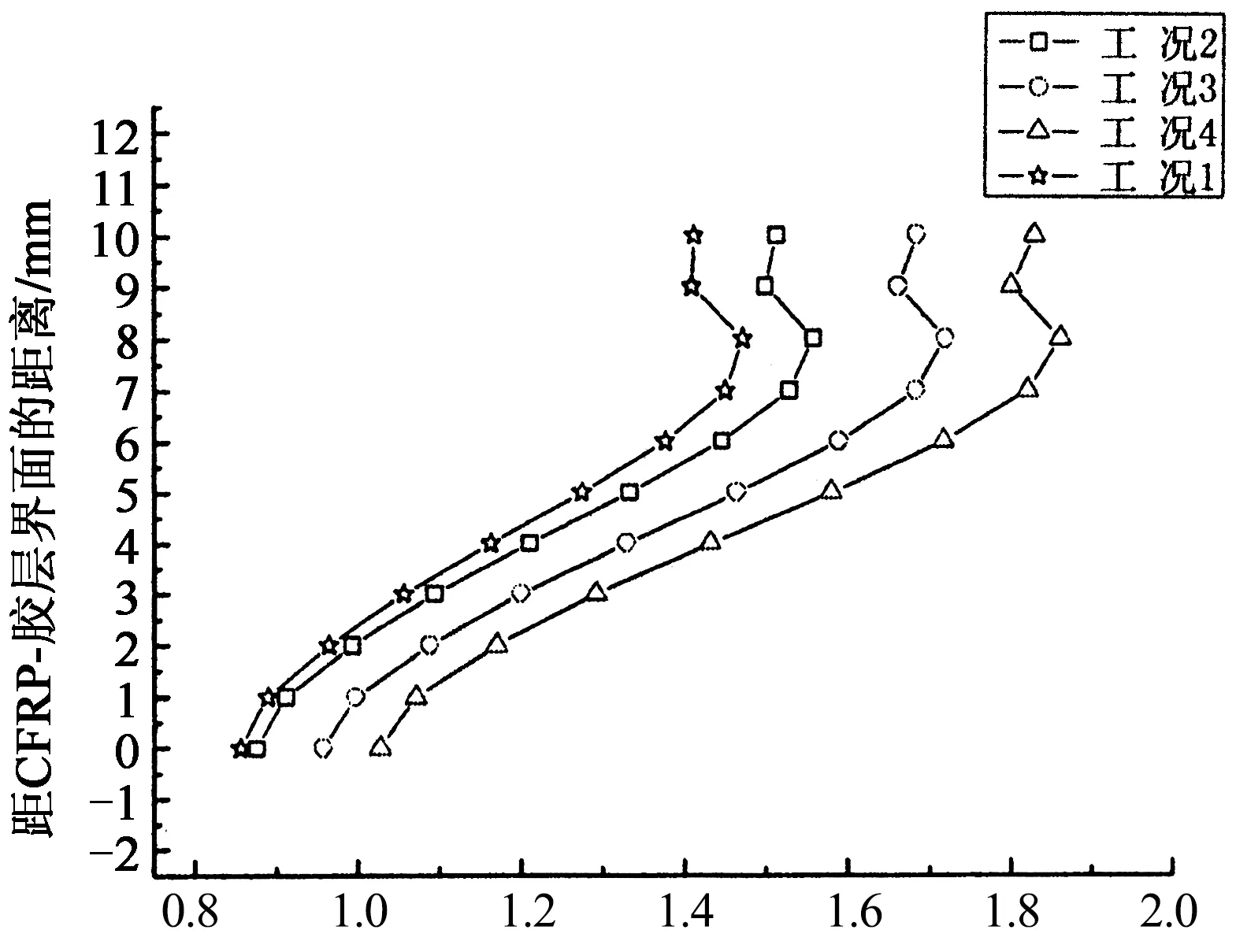
当界面无缺口时，胶层内剪应力和正应力分布如图5(a)(b)所示.可以看出，剪应力分布在端部附近的区域呈现比较明显的非线性，应力值沿厚度方向发生了较大的变化；当到CFRP板端部的距离大于CFRP板长的0.42%(10 mm)时，胶层中剪应力分布已基本呈线性，且随着距离进一步增大，应力沿胶层厚度方向的分布更接近于均匀分布.在CFRP板端部附近区域，正应力分布近似呈线性，简支梁-胶层界面的正应力为拉应力而胶层-CFRP板的界面正应力为压应力，这一结论与Rabinovich等[11]的计算结果一致.随着距离的增大，正应力呈均匀分布.CFRP板端部(x=0)是自由边界，所以端部胶层中应力值较小，趋近于零.加固梁在CFRP板端部(x=0)截面尺寸突变，所以端部胶层中的应力沿厚度方向变化比较剧烈，在远离CFRP板端部区域，胶层中应力较大且其沿厚度方向分布比较均匀.由本文获得界面剪应力和界面正应力的分布情况可知，除了在CFRP板端部附近区域之外，界面应力沿厚度方向为均匀分布.

对于缺口存在的情况，本文选取工况2中缺口位于CFRP板长的1.25%处的情况进行研究，其界面应力分布如图6(a)(b)所示.可以看出，胶层中的剪应力在CFRP板端部附近沿厚度方向呈非线性分布；正应力在CFRP板端部附近沿厚度方向基本呈线性分布.当到CFRP板端部的距离大于CFRP板长的0.42%(10 mm)时，剪应力和正应力沿厚度方向呈近似均匀分布.

在CFRP板端部附近存在缺口时，应力在简支梁与胶层界面和胶层与CFRP板界面的值更大，其应力沿厚度方向分布更加不均匀，变化更剧烈.这是因为CFRP板端部梁截面突变，当缺口位于CFRP板端部附近时，其所导致的应力变化对端部应力分布影响程度最大，当缺口距离CFRP板端部较远时，其对端部应力分布影响较小.在缺口附近，胶层内剪应力和正应力比无缺口情况下相同位置的对应值要小，胶层中的剪应力分布曲线斜率小于无缺口情况下相同位置处的斜率，说明缺口位置处，胶层中的剪应力沿其厚度方向分布更加不均匀.这是因为缺口的存在产生了应力变化现象，使缺口周围的应力分布出现了变化.

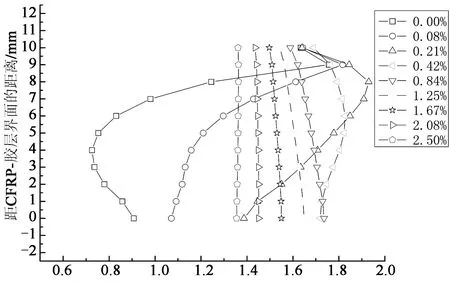
剪应力/MPa (a)胶层剪应力

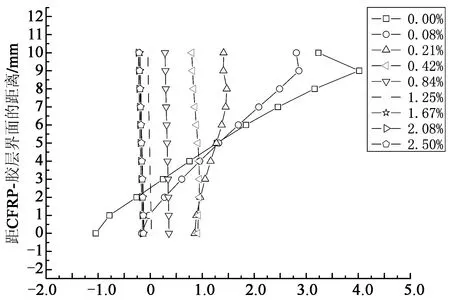
正应力/MPa (b)胶层正应力图5 无缺口情况的胶层应力分布Fig.5 Stress distribution of adhesive layer without notch

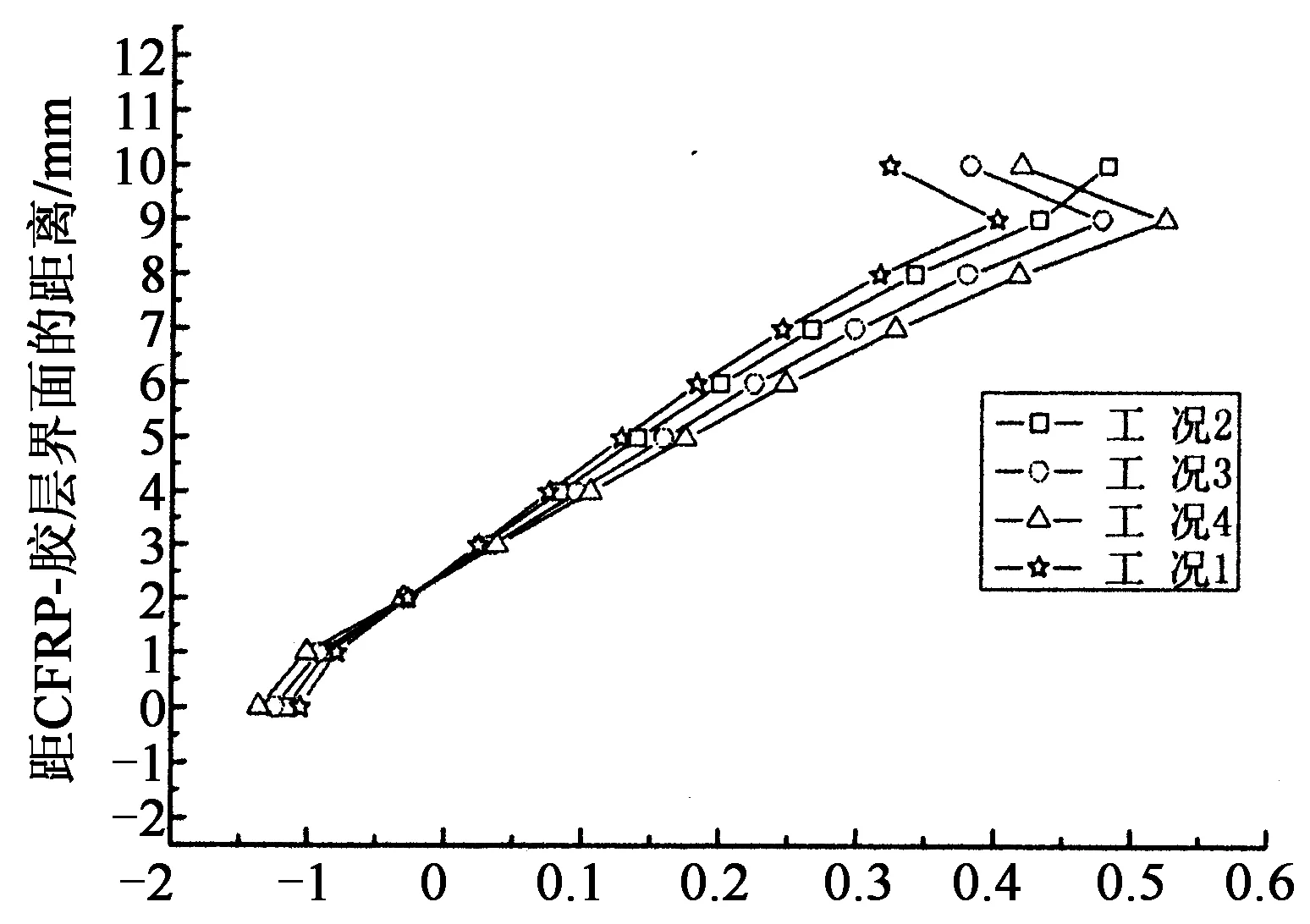
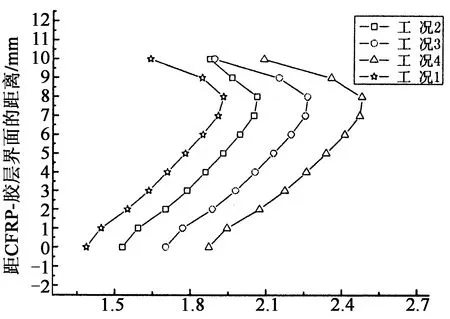
根据2.2节的研究，选取当缺口位于CFRP板长1.25%处研究了缺口深度和宽度对界面应力的影响，发现界面剪应力和界面正应力对缺口深度更加敏感，所以本节选取当缺口位于CFRP板长1.25%处时，研究缺口深度对于胶层中应力分布的影响.图7所示为CFRP板端部和距离CFRP板端部5 mm(0.21%)处的胶层应力分布.分析可知，在CFRP板端部附近剪应力分布呈现明显的曲线分布形态，不同缺口深度的胶层中应力分布曲线的形态相似，随着缺口深度的增大，胶层中剪应力也增大.对于胶层中正应力，其在CFRP板端部(x=0 mm)呈近似线性分布，缺口深度越深，其正应力分布曲线的斜率越小.在距离CFRP板端部5 mm(0.21%)处，不同缺口深度的胶层中应力分布曲线的形态相似.随着缺口深度的增大，胶层中正应力也增大.说明缺口深度只改变应力值大小并不改变胶层中的应力分布特征.

剪应力/MPa (a)胶层剪应力

正应力/MPa (b)胶层正应力图6 有缺口情况的胶层应力分布Fig.6 Stress distribution of adhesive layer with notch

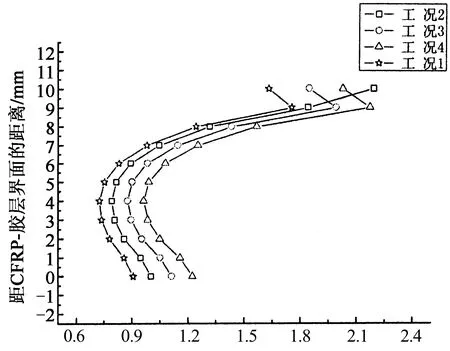
剪应力/MPa (a) CFRP端部(x=0 mm)胶层剪应力

正应力/MPa (b)CFRP端部(x=0 mm)胶层正应力

剪应力/MPa (c)距CFRP端部5 mm(x=5 mm)胶层剪应力

正应力/MPa (d)距CFRP端部5 mm(x=5 mm)胶层正应力图7 不同缺口高度的胶层应力分布Fig.7 Stress distributions of adhesive layer with different notch height

3 结 论

通过对不均匀胶层进行精细化建模分析，研究了CFRP加固钢筋混凝土梁界面不均匀胶层对界面应力及胶层应力的影响.研究得到如下结论：

1)由于梁底部内凹缺口引起的胶层局部变厚导致峰值界面应力和界面应力分布的改变，界面剪应力和正应力的峰值往往出现在距离CFRP板端部较近位置处.当缺口位于CFRP板端部时，峰值界面剪应力和峰值界面正应力均比无缺口情况有所降低.当缺口分别位于CFRP板长0.83%和1.25%处时，峰值界面剪应力和峰值界面正应力分别达到最大值且均高于无缺口情况.缺口距离CFRP板端部越远，峰值界面应力越接近于无缺口情况.缺口导致了界面应力分布曲线在缺口位置处出现波动，波动的幅度和范围与缺口的几何尺寸有关，随着缺口长度的增加，界面剪应力波动幅度增大，正应力波动幅度减小.随着缺口深度的增加，界面剪应力和正应力波动幅度均增大.

2)缺口的几何尺寸对于界面应力有较大的影响.缺口的长度越长或高度越高，峰值界面剪应力和正应力越大.缺口深度对于峰值界面应力的影响大于缺口长度的影响，所以在工程中更应该关注梁底部缺口深度问题.在界面应力达到峰值后，界面应力曲线会经历一个下降段,不同的缺口深度或者长度的界面应力曲线下降段斜率基本相同,在远离缺口的区域界面应力曲线基本吻合,说明缺口几何尺寸并不影响界面应力的分布特征.

3)胶层中的剪应力在CFRP板长0.42%范围内沿其厚度方向呈明显的非线性分布，距离CFRP板端部越远，剪应力越呈均匀分布；胶层中的正应力在CFRP板长0.42%范围内沿其厚度方向呈近似线性的分布，在远离CFRP板端部的位置，正应力呈均匀分布.当有缺口存在时，在CFRP板端部和缺口位置处，其应力沿厚度方向分布得更加不均匀.缺口深度越大，胶层中的应力值越大，但不同高度的缺口其应力分布曲线的形态基本相同，说明缺口深度只改变应力值大小并不改变应力分布特征.

[1] 贺学军. FRP 加固负载混凝土梁的抗弯性能及剥离行为研究 [D]. 长沙: 中南大学土木工程学院, 2007:6-12.

HE Xuejun. Studies on flexural behavior and debonding mechanism of RC beams FRP-strengthened at different preloaded state[D]. Changsha: College of Civil Engineering, Central South University, 2007:6-12. (In Chinese)

[2] 郑文忠, 谭军, 曾凡峰. CFRP 布加固无黏结预应力连续梁受力性能试验研究[J]. 湖南大学学报: 自然科学版, 2008, 35(6): 11-17.

ZHENG Wenzhong, TAN Jun, ZENG Fanfeng. Experimental research on the mechanical property of unbonded prestressed continuous beams reinforced with CFRP sheet[J]. Journal of Hunan University: Natural Sciences,2008,35(6):11-17.(In Chinese)

[3] 滕锦光，陈建飞.FRP 加固混凝土结构[M]. 北京：中国建筑工业出版社, 2005：35-45.

TENG Jinguang, CHEN Jianfei. FRP strengthened RC structures[M]. Beijing: China Architecture & Building Press, 2005：35-45.(In Chinese)

[4] STRATFORD T, CADEI J. Elastic analysis of adhesion stresses for the design of a strengthening plate bonded to a beam[J]. Construction and Building Materials, 2006, 20(1): 34-45.

[5] LU X Z, TENG J G, YE L P,etal. Intermediate crack debonding in FRP-strengthened RC beams: FE analysis and strength model[J]. Journal of Composites for Construction, 2007, 11(2): 161-174.

[6] 尚守平, 李知兵, 彭晖. 碳纤维板-混凝土界面黏结性能的试验研究与有限元分析[J]. 湖南大学学报: 自然科学版, 2014,41(6): 43-51.

SHANG Shouping, LI Zhibing, PENG Hui. Experimental research and finite element analysis of the interfacial bonding behavior of CFRP-concrete interface[J]. Journal of Hunan University: Natural Sciences, 2014,41(6):43-51.(In Chinese)

[7] TENG J G, ZHANG J W, SMITH S T. Interfacial stresses in reinforced concrete beams bonded with a soffit plate: a finite element study[J]. Construction and Building Materials, 2002, 16(1): 1-14.

[8] 张术宽. FRP 加固含缺陷钢结构的破坏力学分析[D]. 广州：华南理工大学土木与交通学院, 2013:15-44.

ZHANG Shukuan. Failure mechanical analyses of cracked steel structures strengthened with FRP[D]. Guangzhou: School of Civil Engineering and Transportation, South China University of Technology, 2013:15-44.(In Chinese)

[9] SMITH S T, TENG J G. Interfacial stresses in plated beams[J]. Engineering Structures, 2001, 23(7): 857-871.

[10]TOUNSI A, DAOUADJI T H, BENYOUCEF S. Interfacial stresses in FRP-plated RC beams: effect of adhered shear deformations[J]. International Journal of Adhesion and Adhesives, 2009, 29(4): 343-351.

[11]RABINOVICH O, FROSTIG Y. Closed-form high-order analysis of RC beams strengthened with FRP strips[J]. Journal of Composites for Construction, 2000, 4(2): 65-74.

[12]SHEN H S, TENG J G, YANG J. Interfacial stresses in beams and slabs bonded with thin plate[J]. Journal of Engineering Mechanics, 2001, 127(4): 399-406.

of Beams Strengthened with CFRP Plate

DU Yunxing†, HOU Chunxu, ZHOU Fen

(College of Civil Engineering, Hunan University, Changsha 410082, China)

Numerical modeling method was adopted to investigate the stress of uneven adhesive layer and the interfacial stresses of the beam strengthened by CFRP plate. The notch was set on the interface of strengthened beam to change the local thickness of adhesive layer. Six cases were set up according to the depth, width and location of the notch. The analysis results indicate that the peak interfacial stresses are much greater than beam without the notch when the notch is located at a short distance from the plate end. When the notch is far from the plate end, the peak interfacial stresses are barely been influenced. The peak interfacial shear and normal stresses reach the maximum values when the notch is located at around 0.83% and 1.25% of the FRP length from the plate end, respectively. With the increase of the length or depth of the notch, interfacial shear and normal stresses increase simultaneously. Both interfacial shear and normal stresses are more sensitive to the change of depth than change of length. The stress distribution of adhesive layer along the thickness-wise direction is uniform except the CFRP plate-end area. When the notch is located at the plate-end area, the notch leads to a stronger variation of stresses of adhesive layer at the plate-end area and also a more non-uniform stress distribution within the notch-area along the thickness-wise direction.

CFRP；notches；finite element analysis；interfacial stress；stress distribution

2016-03-21

国家自然科学基金资助项目(51378199，51108174), National Natural Science Foundation of China(51378199，51108174)

杜运兴(1971-)，男，河南平顶山人，湖南大学副教授, 博士 †通讯联系人，E-mail:duyunxing@hnu.edu.cn

1674-2974(2017)03-0061-07

10．16339/j．cnki．hdxbzkb．2017．03．008

TU312

AEffect of Uneven Adhesive Layer on Interfacial Stress