考虑扰动影响的地基非线性沉降分层总和分析方法*

曹文贵，张超，徐赞,2

(1. 湖南大学 岩土工程研究所，湖南 长沙 410082；2. 湖南城市学院 土木工程学院，湖南 益阳 413000)



考虑扰动影响的地基非线性沉降分层总和分析方法*

曹文贵1†，张超1，徐赞1,2

(1. 湖南大学 岩土工程研究所，湖南 长沙 410082；2. 湖南城市学院 土木工程学院，湖南 益阳 413000)

为预测工程地基土体沉降，针对受到施工扰动影响的地基土，基于扰动状态概念分别以抗剪强度和相对密实度为扰动参量建立扰动因子函数，从而提出能够考虑扰动影响的地基土修正Duncan-Chang模型.首先，考虑地基土实际应力状态，将地基土沉降变形视为由附加静水压力和附加偏应力引起的两部分变形之和，建立地基土沉降变形分析模型；其次，考虑地基土的应力历史并采用分级加载分析方法，给出了不同埋深地基土初始变形模量的确定方法；然后，基于虎克定律和修正Duncan-Chang模型并采用分级加载分析方法分别建立由附加静水压力和附加偏应力作用下的地基沉降变形计算模型，给出了考虑附加应力影响的地基土变形模量的确定方法；最后，将本文方法应用于工程实例并进行了沉降变形分析.研究结果表明：本文方法在反映地基土扰动程度、应力状态和应力历史等方面具有一定的优越性和可行性，其计算结果符合沉降预测规律.

地基沉降；分级加载；扰动；应力状态；应力历史

目前普遍采用传统分层总和法[1]对地基沉降进行分析计算，但是如何准确反映工程地基实际沉降的问题一直未得到很好的解决.因为在施工过程中地基土体不可避免地会受到扰动，使得土体的变形和强度特性发生改变，若采用基于传统分层总和法即通过室内试验获取的土体物理力学参数来预测施工过程中及其后土体变形和强度等特性，则势必造成较大误差，因此，有必要对地基沉降分析即分层总和法作进一步研究.

传统分层总和法基于重塑土固结试验所获得的e-p曲线对土体沉降进行分析计算，然而固结试验所用土样在应力状态、应力历史和扰动程度等方面与实际土体存在较大差异，沉降的最终分析结果需用经验系数加以修正，而经验系数的准确性与个人经验密切相关，因而分析结果难免较为粗糙.为此，基于静载试验的地基沉降分析方法[2-3]应运而生，通过荷载位移p-s曲线获取地基土体的变形模量分析沉降变形，虽然该方法能够反映工程地基土体实际受力变形的特点，但对于缺乏静载试验资料的一般工程就不具有可操作性.由此，众多学者发展了基于土体本构模型[4-9]的地基沉降分析方法，该类方法的关键在于本构模型的合理性以及模型参数的准确性，其中，Duncan-Chang模型[10]能够反映地基土体应力应变的非线性特征，其模型参数少且物理意义明确，不同类别的土体在模型参数取值方面也积累了很多经验，因此，Duncan-Chang模型成为普遍应用的土体本构模型之一．很多学者[7-9]基于该模型对土体沉降变形进行了研究：何昌荣等[7]采用有限元方法测试Duncan-Chang模型各个参数对土坝应力应变的影响程度；何春保等[8]基于荷载位移p-s曲线采用解析方法对土体Duncan-Chang模型参数进行反演分析；曹文贵等[9]根据地基土体非线性变形特征提出了基于Duncan-Chang模型的地基沉降变形分析方法.然而，与大多数土体本构模型一样，传统Duncan-Chang模型无法考虑土体的物理性质，仅能够反映土体的力学状态，故土体一旦受到外界扰动，将会使基于Duncan-Chang模型的地基沉降变形分析结果与实际值相差较大.因此，本文基于扰动状态概念分别以抗剪强度和相对密实度作为扰动参量，对传统Duncan-Chang模型加以修正，以考虑扰动对土体变形力学特性的影响，进而分析地基土体的沉降变形.

由于地基土体的变形力学特性不仅受到外界扰动的影响，还与三向应力及应力历史等因素有关，为此，本文将基于扰动、应力状态和应力历史等方面考虑地基土体的实际应力状态，采用修正Duncan-Chang模型对土体沉降变形进行分析，以期完善地基土体非线性沉降变形分层总和分析方法.

1 修正Duncan-Chang模型

传统Duncan-Chang模型是基于Kondner三轴试验应力应变关系曲线[11]建立的，即

(1)

式中：a=1/Ei；

(2)

b=1/(σ1-σ3)ult.

(3)

由此可看出，a和b分别为初始切线模量Ei和双曲线渐近线所对应极限偏差应力(σ1-σ3)ult的倒数.于是，由式(1)(2)(3)可得:

(4)

研究表明[12-15]地基土体都具有结构性，一旦受到扰动其结构性必然受到影响，相应的物理力学指标都会发生改变，可见，其宏观变形力学特性与结构性密不可分.然而，传统Duncan-Chang模型是基于重塑土三轴应力应变试验曲线建立的，完全打破了土体结构性，使地基土处于完全扰动状态，从而无法反映结构性对土体变形力学特性的影响，与此同时，地基土体又无法避免扰动.由于传统Duncan-Chang模型是能够反映重塑土体变形力学特性的本构模型之一，假如对传统Duncan-Chang模型加以修正使其能够考虑扰动对土体结构性的影响，将会使修正Duncan-Chang模型在地基沉降变形分析方面更具有实际应用价值.由式(4)可知，b(σ1-σ3)为偏应力与极限偏差应力的比率，反映地基土体实际所处应力水平的高低，在地基土体处于相同偏应力水平下，竖向应变会随着极限偏差应力降低(即比率增大)而升高，而极限偏差应力与地基土体结构性所受扰动程度有着显著的关联性，即极限偏差应力会随着扰动程度的增大而发生显著的变化，因此，本文基于扰动状态概念引入扰动因子函数Df对土体极限偏差应力加以修正以考虑扰动程度对极限偏差应力的影响，从而建立修正Duncan-Chang模型，即

(5)

由式(5)可知，能否建立考虑扰动影响的修正Duncan-Chang模型，关键在于建立扰动因子函数的确定方法，但是，扰动对地基土体变形力学特性的影响会因不同类别的土体(黏性土和无黏性土)而有所不同.

对于黏性土，尤其是软土，扰动意味着土体结构性遭到一定程度的破坏，致使土体强度降低以及压缩性增大，这与传统意义上的损伤变量的含义相似，起到弱化土体变形力学性能的作用，属于不利扰动.为此，本文基于土体灵敏度的概念以抗剪强度为扰动参量建立扰动因子函数Df的关系式，即

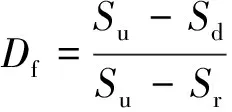
(6)

式中：Su，Sr和Sd分别为原状土、重塑土和受到一定程度扰动的黏性土抗剪强度，可基于十字板剪切试验获得.因Su≥Sd≥Sr，故由式(6)可知黏性土扰动因子函数的取值范围为[0,1]，当扰动因子函数值为1时，修正Duncan-Chang模型即为传统Duncan-Chang模型.

对于无黏性土，尤其是砂土，扰动可以使土体产生微裂隙的损伤(如密砂)，致使土体变形力学性能受到弱化，与黏性土受到扰动影响情况类似，属于不利扰动，扰动因子函数为正值.值得注意的是，扰动也可以使土体得到密实(如松砂)，使土体变形力学性能得到强化，显然此时属于有利扰动，扰动因子函数则为负值.由此可见，扰动对砂土的变形力学特性有正反两方面的作用．砂土三轴试验结果[14-15]表明，相对密实度Dr对砂土峰值强度和应力应变曲线的斜率影响很大，因此，基于扰动状态概念以Dr为扰动参量建立扰动因子函数Df的关系式，即

(7)

式中：Dr0，Drmin和Drmax分别为初始状态、最松散状态和最密实状态的无黏性土相对密实度.将式(6)的函数关系绘制成图，如图1所示．可见，无黏性土扰动因子函数的取值范围为[-1,1]，能够反映无黏性土从初始状态向松散状态(不利扰动)或密实状态(有利扰动)变化的全过程.

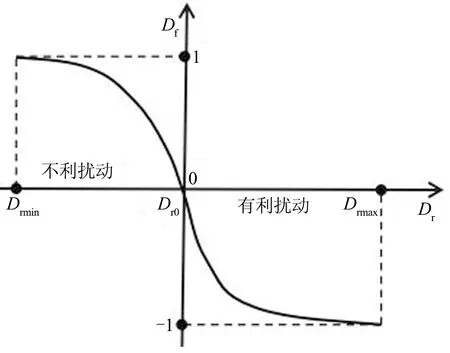
图1 扰动因子与相对密实度关系曲线Fig.1 The relationship curve between disturbance factor and relative density

于是，将不同类别土体的扰动因子函数代入式(5)即得考虑扰动影响的修正Duncan-Chang模型，并在此基础上，考虑地基土体应力状态以及应力历史对土体变形力学特性的影响，建立地基土体沉降变形分析模型.

2 地基沉降变形分析模型

为了能够准确地分析地基土体的沉降变形，必须考虑土体的实际应力状态.由于埋深不同，不同深度的地基土体存在着初始地应力，受到荷载作用又产生附加应力.同时，地基土体存在着强烈的非线性变形即土体变形力学参数会随土体变形而变化，故为了便于分析，在地基基础中心线下取一土体单元(如图2所示)进行应力分析.

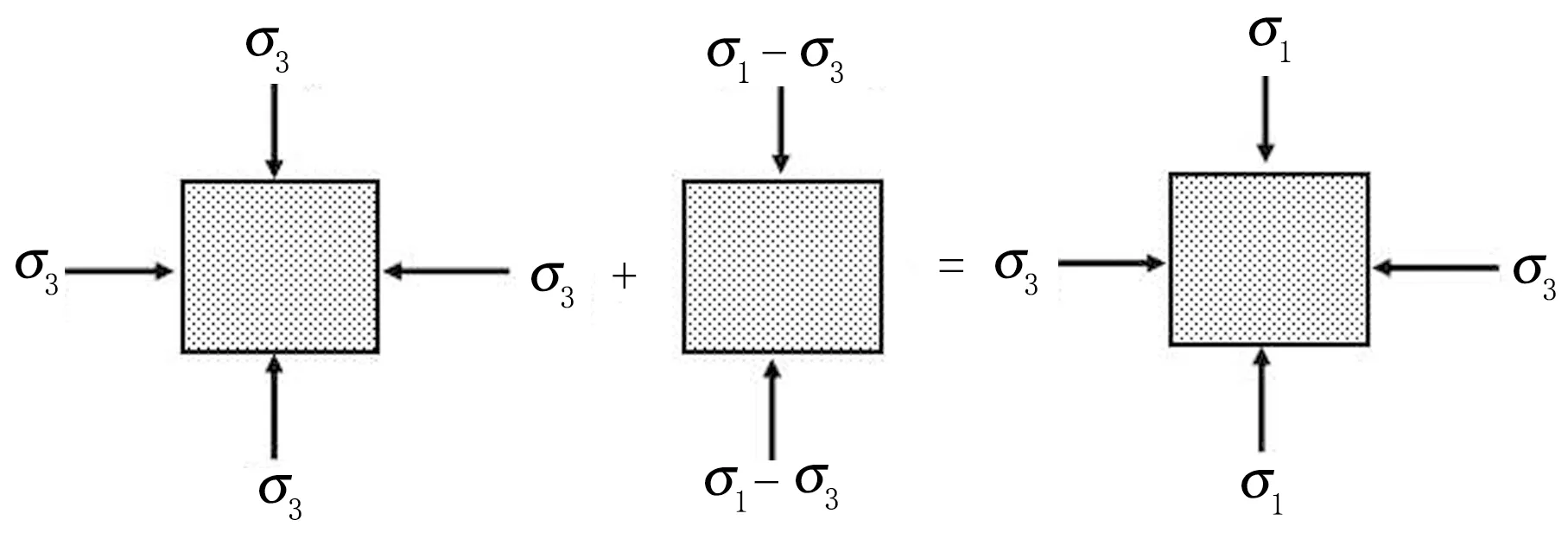
图2 土体单元的应力分析Fig.2 Stress analysis of soil unit

地基土体单元显然处于三向应力状态，基于应力叠加原理，可将土体单元的实际应力状态视为静水压力状态和偏应力状态的叠加.值得注意的是，偏应力状态是基于静水压力状态对土体单元施加的，于是，土体单元在静水压力状态和偏应力状态产生的变形可分别根据广义虎克定律和修正Duncan-Chang模型进行计算.由于地基土体沉降变形是由附加应力作用产生的，基于应变叠加原理，将沉降变形视为土体单元分别处于附加静水压力状态和附加偏应力状态产生的变形之和.于是，各压缩分层土体单元的沉降变形可表示为

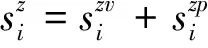
(8)

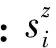
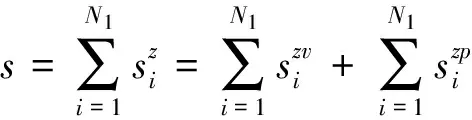
(9)

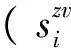
3 地基土体初始变形力学参数

地基土体变形力学参数主要包括变形模量和泊松比，在理论上这2个参数对变形均有影响，但研究表明[7]，泊松比在较小范围变化时对变形计算结果的影响程度很有限，因此本文假定泊松比为常数.由于不同深度的各压缩分层土体在不同初始地应力作用下完成了相应的固结变形，从而使不同埋深的土体具有不同的初始变形模量，因此，基于地基土体单元应力分析可知，初始地应力状态可视为初始静水压力状态和初始偏应力状态的叠加，初始地应力状态引起的固结变形可视为由初始静水压力状态和初始偏应力状态引起的变形累加，而且，土体的固结变形也是一种非线性变形，故本文基于分级加载分析方法对初始变形模量的确定方法分析如下.

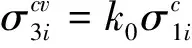
(10)

式中：

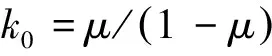
(11)

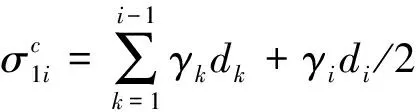
(12)

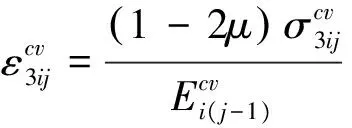
(13)

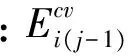
(14)

于是，将式(13)代入式(14)可得到第i层土体在相邻两级初始静水压力作用下的变形模量关系表达式为：

(15)

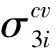
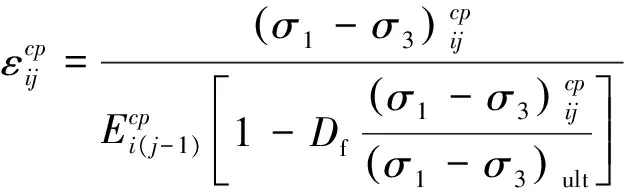
(16)

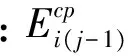
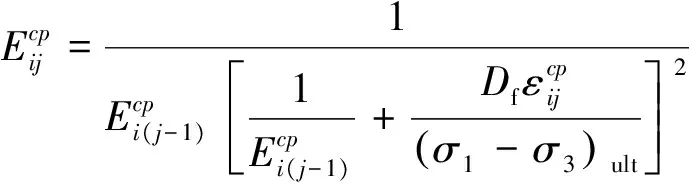
(17)

于是，将式(16)代入式(17)可得第i层土体在相邻2级初始偏应力作用下的变形模量关系表达式为：

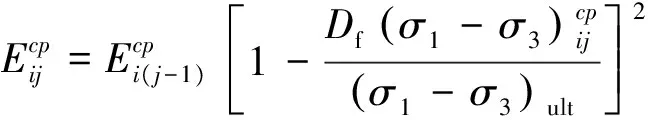
(18)

4 地基土体沉降计算

地基土体在附加应力作用下不断被压密，其变形力学参数不断发生变化，导致地基土体沉降变形具有强烈的非线性特征，采用全量分析法将对土体沉降变形计算带来较大的误差，因此，本文同样基于分级加载分析方法对地基土体在附加应力作用下的沉降变形进行分析计算.由地基土体沉降变形分析模型式(9)可知，需确定地基土体分别在附加静水压力和附加偏应力作用下的沉降变形计算模型.

(19)

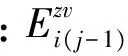
(20)

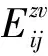
(21)

于是，第i层土体在第j级附加静水压力作用下产生的竖向变形为

(22)

因此，地基土体在附加静水压力作用下的沉降变形计算模型为：

(23)

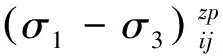
(24)

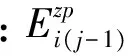
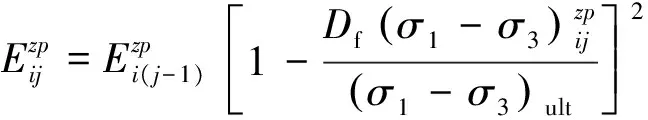
(25)

于是，第i层土体在第j级附加偏应力作用下产生的竖向变形为

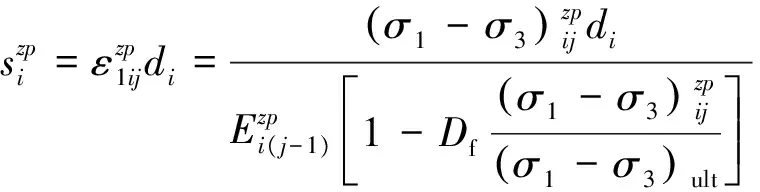
(26)

因此，地基土体在附加偏应力作用下的沉降变形计算模型为：

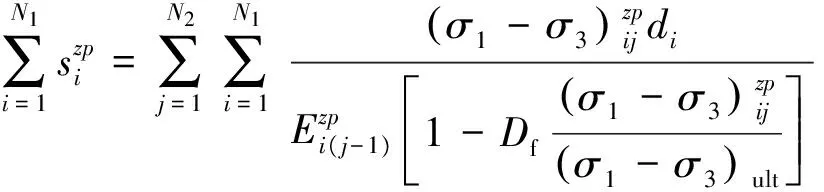
(27)

最后，通过地基土体分别在附加静水压力和附加偏应力作用下的沉降变形计算模型即式(23)和式(27)求得相应的沉降变形，并代入式(9)可得地基土体的总沉降变形.

5 工程实例

为了验证本文方法的合理性与可行性，引用文献[18-19]工程资料进行分析，其分析步骤如下.

1)根据工程资料确定地基土体的扰动因子，按第1节方法进行；

2)确定考虑应力历史影响的各压缩分层地基土体的初始变形模量，按第3节方法进行；

3)根据沉降变形计算模型确定在附加应力作用下各压缩分层地基土体的沉降变形，并得到地基土体的总沉降变形，按第4节方法进行；

4)将本文地基土体沉降变形计算结果与实测结果进行比较分析，以验证本文方法的合理性与可行性.

5.1 工程实例1

某软土地基上填筑路堤[18]，堤身分别由1.5 m厚、平均重度为17.23 kN/m3的淤泥质土和2.5 m厚、平均重度为19.86 kN/m3的花岗岩风化土组成; 软土地基由2 m厚的浅层土和10 m厚的深层土组成，其物理力学指标见表1.堤身填土为分级加载，据观测，地基中心点沉降为100 cm.

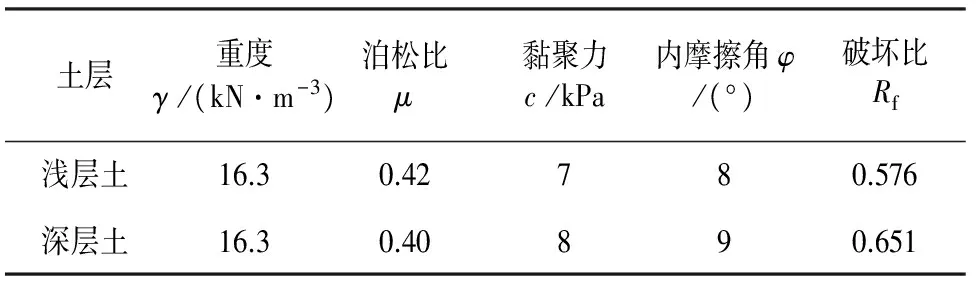
表1 土体的物理力学参数Tab.1 Physical and mechanical parameters of soils

1)由于文献[18]缺乏实测地基土体扰动资料，且文献[20]研究表明，扰动对地基土体的影响程度随深度增大而减小，因此本文为了便于比较分析，假定扰动因子按深度加权后分别为0.5,0.7,0.9,1.0等4种工况，然后，采用修正Duncan-Chang模型对土体变形分别进行分析计算.

2)根据分层总和法对计算深度和分层厚度的要求，确定计算深度为12 m，每层厚度为1.0 m，即压缩层数N1=12.

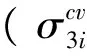
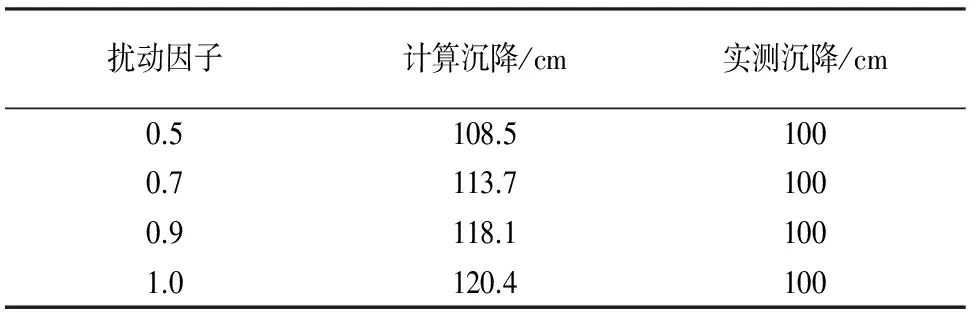
表2 实测值与不同扰动因子下沉降计算值比较(不利扰动)Tab.2 Comparison between measured values and calculated values under different disturbance factors(adverse disturbance)

5.2 工程实例2

某试验场地位于A&M大学国家岩土试验站[20]，该场地地基土层为均质中等密实含泥细砂，地下水位埋深4.9 m，砂土重度为19.5 kN/m3，泊松比为0.25，内摩擦角为32°，压缩模量为30.0 MPa．在该砂土地基上进行3 m×3 m浅基础现场原位试验，经测试可知，当荷载为1.0×104kN时基础中心点沉降变形量为120 mm.

从安全角度考虑，破坏比在本文中取1.0.由于试验资料同样缺乏地基土体扰动资料，因此本文为了便于分析，假定平均扰动因子分别取-0.5,-0.7,-0.9等3种工况对地基土体变形进行分析计算.同时，原始资料只给出压缩模量和泊松比，因此，本文只能采用变形模量与压缩模量之间的关系进行换算得到砂土的变形模量，其余计算过程与工程实例一类似，其结果如表3所示.

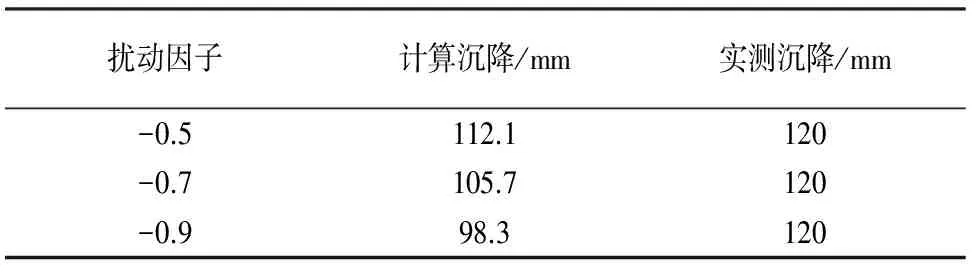
表3 实测值与不同扰动因子下沉降计算值比较(有利扰动)Tab.3 Comparison between measured values and calculated values under different disturbance factors(favorable disturbance)

由上述2个工程实例分析可见，对于受到正扰动(不利扰动)的软土地基，由于结构性遭到了破坏，压缩性变大，因此软土地基沉降变形随着不利扰动程度增大而增大；对于受到负扰动(有利扰动)的砂土地基，由于扰动使砂土变得更加密实，土体变形减小，故砂土地基沉降变形随着有利扰动程度增大而减小.由此可见，2个工程实例计算结果符合地基土体沉降预测规律.

6 结 论

本文从地基沉降变形机理研究入手，考虑扰动程度、应力状态和应力历史对地基土体非线性变形的影响，基于叠加原理将地基沉降变形视为附加静水压力和附加偏应力引起的2部分变形之和，采用分级加载分析方法通过虎克定律和修正Duncan-Chang模型对地基土体的变形力学参数和沉降变形进行了深入探讨，得到如下结论：

1)本文基于扰动状态概念以抗剪强度和相对密实度为扰动参量建立扰动因子函数表达式，从而建立了能反映土体物理力学状态即能考虑扰动影响的修正Duncan-Chang模型.

2)通过分析地基土体的应力状态和应力历史，建立地基土体沉降变形分析模型并给出了考虑初始地应力和附加应力影响的变形模量确定方法.

3)采用分级加载分析方法建立基于虎克定律和修正Duncan-Chang模型的地基土体沉降变形计算模型，弥补了室内固结e-p试验曲线和地基静载p-s试验曲线的不足.

4)工程实例分析表明，本文沉降变形计算分析方法具有一定的合理性与可行性.

[1] 赵明华，俞晓，王贻荪. 土力学与基础工程[M]. 武汉: 武汉理工大学出版社, 2003：63-66.

ZHAO Minghua, YU Xiao, WANG Yisun. Soil mechanics and foundation engineering[M]. Wuhan: Wuhan University of Technology Press, 2003：63-66. (In Chinese)

[2] 杨光华. 地基非线性沉降计算的原状土切线模量法[J]. 岩土工程学报, 2006, 28(11): 1927-1931.

YANG Guanghua. Nonlinear settlement computation of the soil foundation with the undisturbed soil tangent modulus method[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1927-1931. (In Chinese)

[3] 李仁平. 用双曲线切线模量方程计算地基非线性沉降[J].岩土力学, 2008, 29(7): 1987-1992.

LI Renping. Nonlinear ground settlement calculated by hyperbolic curve tangent modulus equation[J]. Rock and Soil Mechanics, 2008, 29(7): 1987-1992. (In Chinese)

[4] 曹文贵，田小娟，刘海涛，等. 条形基础下地基非线性沉降的改进计算方法[J].岩石力学与工程学报，2009,28(11):2262-2272.

CAO Wengui, TIAN Xiaojuan, LIU Haitao,etal. Improved method for calculating nonlinear settlements of strip foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(11):2262-2272. (In Chinese)

[5] 何思明. 基于弹塑性理论的修正分层总和法[J].岩土力学，2003, 24(1):88-92.

HE Siming. Modified layer-summation based on elastoplastic theory[J]. Rock and Soil Mechanics, 2003, 24(1):88-92. (In Chinese)

[6] 曹文贵，唐旖旎，王江营. 基于孔隙介质模型的散体材料桩复合地基沉降分层总和分析方法[J].湖南大学学报:自然科学版，2014，41(11):87-95.

CAO Wengui, TANG Yini, WANG Jiangying. A layer-wise summation analysis method for the settlement of composite ground with friable material piles based on porous medium model[J]. Journal of Hunan University: Natural Sciences, 2014,41(11):87-95. (In Chinese)

[7] 何昌荣，杨桂芳. 邓肯-张模型参数变化对计算结果的影响[J]. 岩土工程学报, 2002, 24(2): 170-174.

HE Changrong, YANG Guifang. Effects of parameters of Duncan-Chang model on calculated results[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 170-174. (In Chinese)

[8] 何春保，沈建华，蔡健，等. Duncan-Chang非线性地基模型的反演分析[J]. 岩土工程学报, 2009, 31(4): 634-638.

HE Chunbao, SHEN Jianhua, CAI Jian,etal. Back analysis of Duncan-Chang nonlinear foundation model[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 634-638. (In Chinese)

[9] 曹文贵，邓湘君，张超. 基于Duncan-Chang模型的地基沉降分层总和分析方法探讨[J].岩土工程学报，2013,35(4):643-649.

CAO Wengui, DENG Xiangjun, ZHANG Chao. Layerwise summation method for ground foundation settlement based on Duncan-Chang constitutive model[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(4):643-649. (In Chinese)

[10]DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1970, 96(SM5): 1629-1653.

[11]KONDNER R L. Hyperbolic stress-strain response cohesive soils [J]. Journal of the Soil Mechanics and Foundation, ASCE, 1963, 89(SM1): 115-143.

[12]沈珠江. 结构性黏土的弹塑性损伤模型[J]. 岩土工程学报，1993,15(3):21-28.

SHEN Zhujiang. An elasto-plastic damage model for cemented clays[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3):21-28. (In Chinese)

[13]陈铁林，陈生水，周成. 黏土结构性参数测定研究[J].岩土工程学报，2008，30(8):1146-1151.

CHEN Tielin, CHEN Shengshui, ZHOU Cheng. Study on parameter determination of structured clays [J]. Chinese Journal of Geotechnical Engineering, 2008，30(8):1146-1151. (In Chinese)

[14]朱剑锋. 考虑扰动影响的土体性状研究[D]. 杭州：浙江大学建筑工程学院，2011:13-23.

ZHU Jianfeng. Study on properties of soil considering disturbance[D]. Hangzhou: College of Civil Engineering and Architecture, Zhejiang University, 2011:13-23. (In Chinese)

[15]朱剑锋，徐日庆，王兴陈，等. 考虑扰动影响的砂土弹塑性模型[J]. 岩石力学与工程学报，2011, 30(1):193-201.

ZHU Jianfeng, XU Riqing, WANG Xingchen,etal. An elastoplastic model for sand considering disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1):193-201. (In Chinese)

[16]陈昌富，曹虹，王纯子，等.下卧倾斜硬层对非均布荷载下地基沉降的影响[J].湖南大学学报:自然科学版，2014,41(6):77-84.

CHEN Changfu, CAO Hong, WANG Chunzi,etal. Influence of inclined bedrock on subgrade settlements under non-uniformly distributed load[J]. Journal of Hunan University: Natural Sciences, 2014,41(11):77-84.(In Chinese)

[17]曹文贵, 刘海涛, 张永杰. 散体材料桩复合地基沉降计算的分层总和法探讨[J]. 水利学报, 2010, 41(8): 984-990.

CAO Wengui, LIU Haitao, ZHANG Yongjie. Study on layer-wise summation method of settlement computation for composite foundation with friable material piles[J]. Journal of Hydraulic Engineering, 2010, 41(8): 984-990. (In Chinese)

[18]彭长学，杨光华.软土e-p曲线确定的简化方法及在非线性沉降计算中的应用[J]. 岩土力学, 2008, 29(6): 1706-1710.

PENG Changxue, YANG Guanghua. A simplified method for determininge-pcurve of soft soil and its application to analyzing nonlinear settlement of foundation[J]. Rock and Soil Mechanics, 2008, 29(6): 1706-1710. (In Chinese)

[19]BRIAUD J L, GIBBENS R. Behavior of five large spread footings in sand [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(9):787-796.

[20]施建勇，赵维炳，顾吉，等.考虑损伤的软土地基分析[J]. 岩土工程学报, 1998, 20(2): 2-5.

SHI Jianyong, ZHAO Weibing, GU Ji,etal. Analysis of deformation of soft ground considering damage[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 2-5. (In Chinese)

of Ground Foundation Considering Disturbance Effect

CAO Wengui1†，ZHANG Chao1，XU Zan1, 2

(1.Geotechnical Engineering Institute, Hunan University, Changsha 410082, China;2. College of Civil Engineering, Hunan City University, Yiyang 413000, China)

For the ground foundation influenced by the construction disturbance, the disturbance factor functions taking the shear strength and relative density as the disturbed parameters, respectively, were proposed based on the disturbed state concept. By using this function, a modified Duncan-Chang model considering the influence of disturbance was developed to provide a reference for the settlements prediction of ground foundation. Firstly, considering the stress state of ground soil, the analytical model for ground soil was established by idealizing the ground settlement to be the summation of one part caused by additional hydrostatic pressure and the other part by additional deviatory stress. Secondly, considering the stress history of ground soil, the determination method for initial deformation modulus of ground soil at different depths was provided by using the step-loading analysis method. Based on the Hooke’s law and modified Duncan-Chang model, the models to evaluate the settlement of ground foundation caused by additional hydrostatic pressure and of that by additional deviatory stress were then developed, respectively, by using the step-loading analysis method. The determination method for deformation modulus of ground soil was also given considering the additional stress effect. Finally, the proposed method was applied to a practical project case, and the corresponding settlement analysis was carried out. The results show that the proposed method has superiority and feasibility in the aspects of reflecting disturbance degree, stress state and stress history. The calculated results agree well with the prediction rule of settlement.

foundation settlement; step-loading; disturbance; stress state; stress history effects

2016-02-27

国家自然科学基金资助项目(51378198)，National Natural Science Foundation of China(51378198)；高等学校博士学科点专项科研基金资助项目(20130161110017), Research Fund for the Doctoral Program of Higher Education of China(20130161110017)

曹文贵(1963-)，男，湖南南县人，湖南大学教授，博士生导师 †通讯联系人，E-mail: cwglyp@21cn.com

1674-2974(2017)03-0113-07

10．16339/j．cnki．hdxbzkb．2017．03．014

TU44

ALayer-wise Summation Method for Nonlinear Settlements