悬索桥钢桁梁断面质量惯性矩简化计算方法*

华旭刚，杨坤，温青，陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)



悬索桥钢桁梁断面质量惯性矩简化计算方法*

华旭刚†，杨坤，温青，陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)

鱼骨单主梁模型是分析大跨度钢桁梁悬索桥抗风性能的常用简化模型.针对由于悬索桥钢桁梁断面杆件众多造成的其扭转质量惯性矩计算繁琐、精度低的问题，提出一种基于均匀附加扭转质量惯性矩前后结构扭转频率的变化计算钢桁梁扭转质量惯性矩的方法，并给出了该方法的理论说明、适用条件等.以一钢桁梁悬臂结构为例进行了数值仿真，结果表明：附加扭转质量惯性矩施加在全截面或上、下弦杆节点，且钢桁梁的长细比L/D≥20时，该方法计算的扭转质量惯性矩有较高的精度.采用该方法计算了多座钢桁梁悬索桥的主梁扭转质量惯性矩，比较了全桁架模型和单主梁模型扭转振动频率，验证了方法的有效性.

钢桁梁；悬索桥；扭转质量惯性矩；抗风设计

钢桁梁具有刚度大、用钢量省、适应双层桥面、抗风性能良好等优点，在国内外大跨度悬索桥中得到广泛应用，如香港青马大桥[1]、美国的金门大桥[2]、日本的明石海峡大桥[3]等.在钢桁架为主梁的悬索桥的主梁节段模型试验中，通常采用节段模型测力法获得钢桁梁断面的静三分力或颤振导数.为与节段模型测力法相适应，需要建立钢桁梁的等效单主梁模型.钢桁梁断面的扭转质量惯性矩是建立等效单主梁模型的一个重要参数，其计算的精确与否将直接影响等效单主梁模型的扭转频率、振型等参数，因此，如何快捷、有效地计算钢桁梁的扭转质量惯性矩显得尤为重要.

钢桁梁通常由数量众多的薄壁工字型或箱型截面构件构成，由上下弦杆、腹杆、平纵联及横联等组成.沿桥跨方向，由于不同位置处的横断面的差异性，造成其质心沿桥跨方向也在不断变化，故很难精确计算钢桁梁的扭转质量惯性矩.常规方法是找到节点处横断面的质心位置，并假定沿桥跨方向各横断面质心位置不变，然后计算钢桁梁的扭转质量惯性矩，并以此作为单主梁模型扭转质量惯性矩的初值，不断调整单主梁模型中此参数，来使全桁架模型与单主梁模型中的扭转频率一致[4].这种方法缺乏理论基础，主观性大，且计算繁琐.于永帅[5]提出一种简化算法：通过在钢桁梁上沿桥跨方向均匀附加扭转质量惯性矩，利用附加质量惯性矩前后2次动力特性的变化反算钢桁梁自身扭转质量惯性矩.这种方法思路清晰，计算便捷，但其对此方法的理论证明、适用条件、附加扭转质量惯性矩的施加位置等未作详细研究.

基于此，本文对该方法作进一步研究.首先，阐述了悬索桥风振分析所用有限元模型的特征，说明了计算扭转质量惯性矩的重要性和必要性；然后，详细地讨论了本文提出的钢桁梁断面扭转质量惯性矩的计算方法，并给出了该方法的理论说明和适用条件；接着，通过数值仿真，分析了钢桁梁的长细比、附加扭转质量惯性矩的施加位置对计算结果的影响；最后，应用该方法计算了多座钢桁梁悬索桥的主梁等效扭转质量矩，并验证了结果的可靠性.

1 悬索桥动力分析模型

随着现代大跨桥梁的日渐轻柔化，悬索桥及斜拉桥的抗风抗震性能越来越受到人们的关注，这方面的研究必须借助三维有限元分析方法[6].我们可以采用由多种单元(包括梁单元、板单元、壳单元等)组合的有限元方法对悬索桥进行分析，但这种方法必会涉及大量的运算，当采用时域法进行随机动力分析时，为了得到大量样本的统计结果，这个问题显得尤为突出，且往往是行不通的[7].为此，必须将结构的刚度、质量、边界条件等根据一定的等效原则对结构进行一定的抽象和简化，建立实用的动力分析模型.目前常用的简化模型有单主梁、双主梁、三主梁模型以及实体块或板壳单元模型[7-9].

单主梁模型把桥面系的刚度(竖向、横向挠曲刚度、扭转刚度)和质量(平动质量和转动惯量)都集中在中间节点上，节点和吊杆之间采用刚臂连接或处理为主从关系.单主梁模型适用于自由扭转刚度较大的闭口截面主梁.这种模型的优点是主梁的刚度和质量模拟较为准确，且计算量小；缺点是横梁的刚度和主梁的翘曲刚度未能得到充分考虑.

双主梁模型将主梁的竖向刚度平均分配给2根边主梁以保证竖向刚度的等效，可近似地考虑主梁约束扭转的贡献，适合于开口或半闭口截面的主梁，缺点是对侧向刚度和约束扭转刚度的模拟不准确.

三主梁模型是目前较完善的一种桥面系模型，它通过适当的刚度和质量分配来满足等效原则，可以克服上述2种模型的缺点，但使用三主梁模型会使结构离散的单元数大大增加，这对于抗风计算的时域分析的求解效率是十分不利的.

实体块或板壳单元模型中，主梁采用体板单元模拟，能较准确地计算结构整体和局部的变形和内力.其缺点是计算量相当大，对计算机硬件的要求比较高[10].

钢桁梁具有较大的扭转刚度，且考虑到后续风振响应分析、气弹模型的设计，需要采用单主梁计算模式模拟钢桁架结构.

2 扭转质量惯性矩

2.1 扭转质量惯性矩的定义

扭转质量惯性矩，简称质量惯性矩或质量矩，又叫转动惯量，是刚体动力学中的一个重要概念，它表征物体转动惯性的大小.为叙述方便，下文均采用质量矩.

质量矩为空间中质量关于距离的二次矩.对于离散体系，它对空间任意一条直线z的质量矩定义为：

(1)

式中：mi表示第i个质量块的质量；ri表示第i个质量块到直线z的距离.

对于连续体，则可用积分表示为：

Im=∫r2dm.

(2)

式中：r表示质量微元dm到z轴的距离.

以矩形闭口薄板(如图1所示)为例，可以通过面积分得到其计算公式为

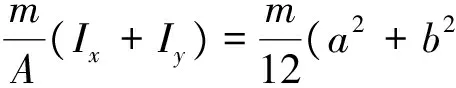
(3)

式中：ρ表示矩形薄板的面密度；m表示矩形薄板的质量；A表示矩形薄板的面积；Ix和Iy分别表示矩形薄板关于x轴、y轴的惯性矩；a，b分别表示矩形薄板的长和宽.然而，桁架断面由于质量沿空间分布不均匀，故不能用公式(3)计算.

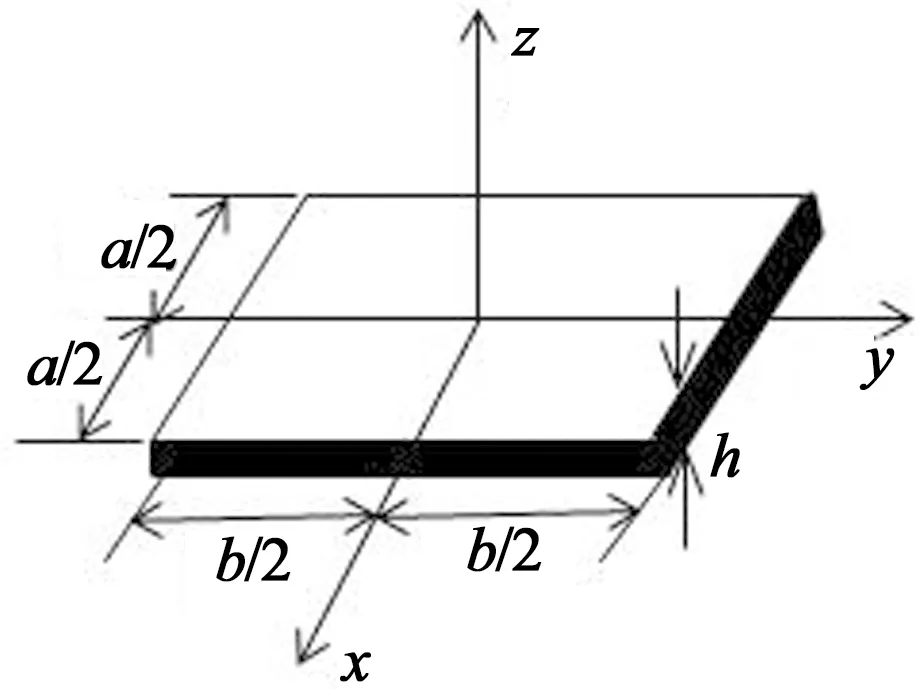
图1 矩形薄板Fig.1 Thin rectangular plate

2.2 简化算法

2.2.1 计算原理

本文提出的是一种基于均匀附加质量矩前后结构动力特性的变化计算钢桁梁质量矩的方法.该方法采用质量矩均匀分布的悬臂梁模型，通过在钢桁梁上沿桥跨方向均匀附加质量矩，然后根据附加质量矩前后悬臂梁扭转频率的变化反算钢桁梁自身的质量矩，下面对该理论进行详细说明.

2.2.2 理论证明

为下文证明方便，限制悬臂梁模型的平动自由度，并将其离散化为只有扭转自由度的N自由度体系，如图2所示.

图2 只有扭转自由度的悬臂梁的离散化Fig.2 The discretization of the cantilever girder with only torsional degree of freedom

该悬臂梁模型的运动方程为

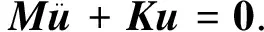
(4)

令u=Ucosωt，并代入式(4)，得

(K-ω2M)U=0.

(5)

式中：K为N阶刚度方阵，质量矩阵M为N阶对角阵，考虑到U不全为零，故式(5)是一个特征值问题.对式(5)进行特征值求解，得ωr与φr，(r=1，2,…，N)分别为特征值和其对应的特征向量.

因为悬臂梁质量矩均匀分布，故

M=ImE.

(6)

式中:Im为每个节段的质量矩; E为N阶单位阵.

在每个节段上均附加大小为ΔIm的质量矩，令

α=ΔIm/Im,

(7)

则此时质量矩阵M*为

M*=M+ΔImE=(Im+ΔIm)E=(1+α)M，

(8)

此时，系统动力方程为

[K-(1+α)ω2M]U=0.

(9)

由式(5)(9)知，特征值矩阵即弹性矩阵 K未发生变化，且质量矩阵M为N阶对角阵，因此特征向量不变，即附加质量矩前后，结构的扭转振型不变.

由瑞利法可知，未附加质量矩时，结构的扭转基频ω1为：

(10)

式中:φ1为第一阶扭转振型; K为N阶刚度方阵; M为N阶质量方阵; k1和m1分别是第一阶模态刚度和模态质量.由于模态振型φr为任意尺度的无量纲特征向量，不同的模态振型尺度，模态质量mr和模态刚度k1不同，因此通常需要对振型进行规格化，常用的振型规格化方法有2种[11]：1)按质量归一化的振型规格化，即结构的模态质量为mr=1；2)特定自由度幅值取1的振型规格化，即某个自由度的幅值取1，并以这个指定的值为基准确定其他自由度幅值，如指定最大自由度幅值为1.本文采用指定最大自由度幅值为1的方法对振型进行规格化.

在每个节段上均附加大小为ΔIm的质量矩，前面已经证明了质量矩均匀分布的悬臂梁模型附加质量矩前后，结构的扭转振型不变，因此扭转基频变为ω1*，

(11)

比较式(10)和式(11)，并将式(6)(7)(8)代入，可得：

整理上式得：

(12)

式中：Im表示钢桁梁各节段质量矩大小；ΔIm表示钢桁梁各节段附加的质量矩大小；ω1，ω1*分别表示质量矩附加前后的悬臂钢桁梁的一阶扭转圆频率；f1，f1*分别表示质量矩附加前后的悬臂钢桁梁的一阶扭转频率.

公式(12)就是计算质量矩的依据.为方便使用，现将该方法计算步骤概括如下：

1)建立适当长度的钢桁梁有限元模型，使其处于悬臂状态，计算一阶扭转频率f1；

2)沿梁跨方向在钢桁梁模型上各节段处附加质量矩大小均为ΔIm的扭转质量单元，并计算一阶扭转频率f1*；

3)利用公式(12)计算钢桁梁各节段的扭转质量惯性矩Im.

2.2.3 适用条件

由证明过程知，结构的质量矩需要满足其沿梁跨均匀分布，且沿梁跨方向在各节段施加的附加质量矩大小相同.

3 数值仿真分析

为了验证简化算法的可行性和计算结果的精确性，通过ANSYS对影响钢桁梁质量矩计算结果的因素进行分析.

3.1 有限元模型

主梁采用板桁结合型钢桁加劲梁，主桁架为带竖腹杆的华伦式结构，由上弦杆、下弦杆、竖腹杆和斜腹杆组成.主桁桁高9m，桁宽35.4m，节间长度8.4m.在主桁架每个节点处设置一道主横桁架，下平联采用K形体系，节点处横断面如图3所示.

建立有限元模型时，上下弦杆、腹杆、平纵联、横梁等采用beam188单元，桥面板采用shell63单元.为验证该方法所计算结果的正确性，两者的密度均取为0，两者的扭转质量惯性矩通过mass21单元施加，各节段(节段长度为8.4m)质量矩Im均取为4.028×107kg·m2，具体到各节点的质量矩大小见表1(考虑到桥面板的影响，故顶层节点的质量矩较大).建立加劲梁有限元模型如图4所示，后处理时质量矩阵采用集中质量矩阵.

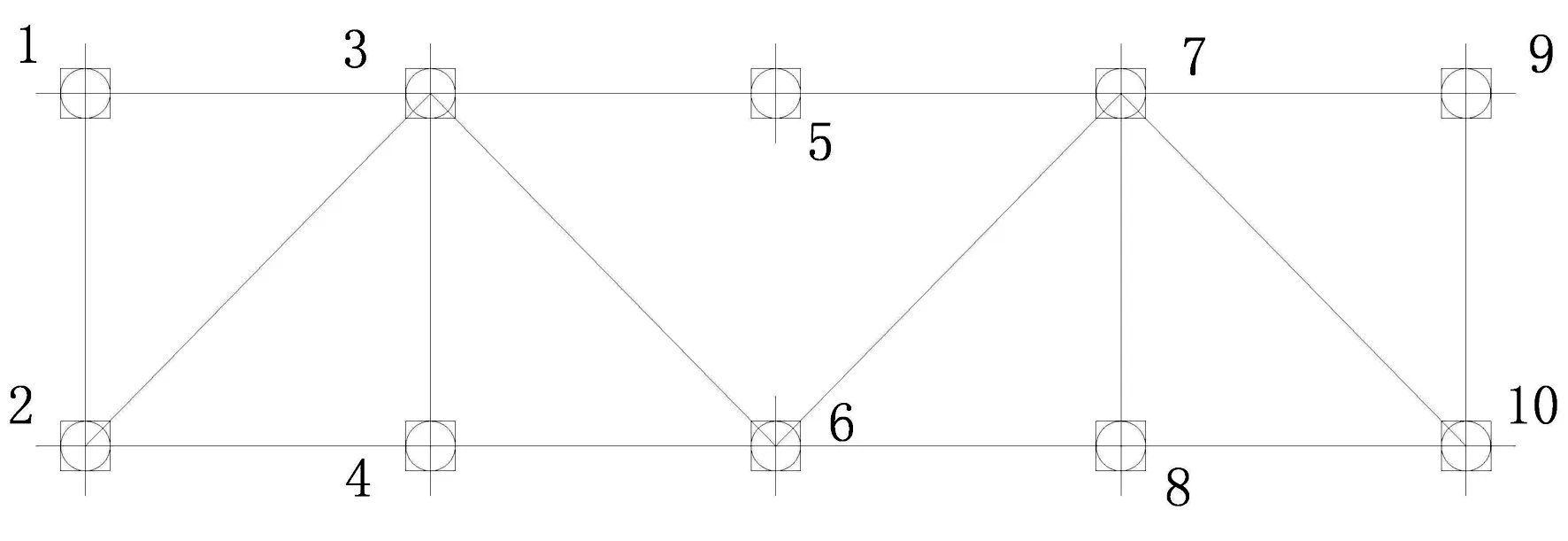
图3 钢桁梁节点处横断面Fig.3 Node cross section of the stiffening truss girder表1 各节点质量矩大小Tab.1 Mass moment of inertia of each node

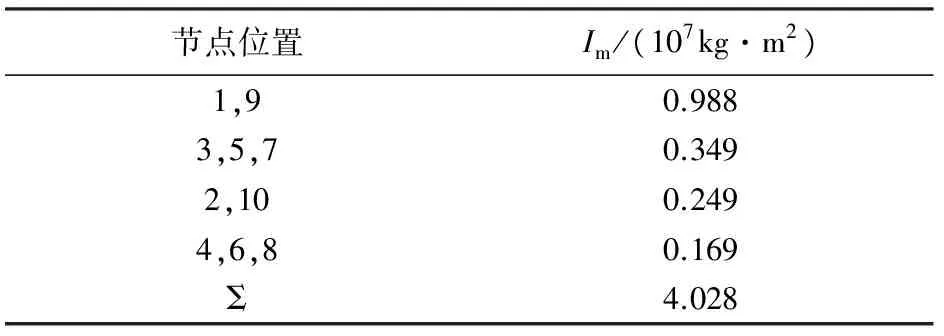
节点位置Im/(107kg·m2)1，90．9883，5，70．3492，100．2494，6，80．169Σ4．028

图4 钢桁梁有限元模型Fig.4 Finite element model of the stiffening truss girder

3.2 影响因素

钢桁梁质量矩计算结果的主要影响因素有2个，一是钢桁梁的长细比L/D(L表示钢桁梁的长度，D表示钢桁梁宽度和高度的较大值)，二是附加质量矩的施加位置.

1)钢桁梁的长细比: 钢桁梁为组合结构，从单一杆件分析，各杆件受力以轴力为主，可近似看成二力杆；但从整体来看，主桁上、下弦杆以及平、纵联在适当间距内提供了桁架承受较大弯矩的能力；横梁和上下平联连接2片主桁能够提供整体抗扭刚度.当钢桁梁长度远大于梁宽度和梁高度时，桁架结构成为一个具有明显梁特性的单梁[4].

为研究钢桁梁的长细比对质量矩计算结果的影响，选取长细比分别为L/D≈10(L=352.8 m)，20(L=740 m)和55(L=1 933.6 m)的3个钢桁梁进行计算.

2)附加质量矩施加位置：桁架横断面有多个节点，在不同节点处附加质量矩对计算结果可能会产生影响.原桁架横断面左右对称，故附加质量矩应左右对称施加，在不同位置处附加质量矩时的工况见表2.

表2 附加质量矩施加位置Tab.2 Position of additional mass moment of inertia

3.3 计算结果

利用简化算法可以得到钢桁梁的质量矩(称为计算值)，将计算值与真实值(见表1)作比较，得到计算误差，如图5—图7所示.钢桁梁取不同长细比时，用简化算法计算其质量矩过程相似，所以仅给出了L/D=10时工况一的计算步骤，见表3.这里，ΔIm表示钢桁梁各节段的附加质量矩大小，fi表示悬臂钢桁梁的一阶扭转频率，Im表示钢桁梁各节段的质量矩大小.为保证计算结果的稳定性，计算时选取了不同大小的附加质量矩.

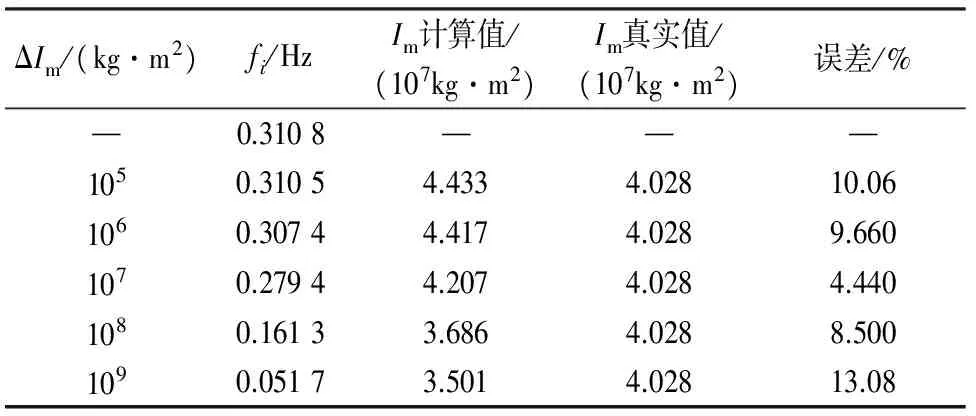
表3 L/D=10时质量矩计算表Tab.3 L/D=10, calculation processof mass moment of inertia

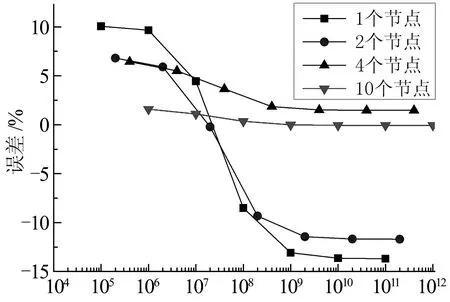
附加质量矩/(kg·m2)图5 L/D=10时质量矩计算误差Fig.5 L/D=10, mass momentof inertia calculation error

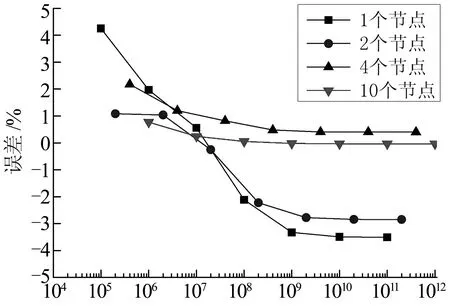
附加质量矩/(kg·m2)图6 L/D=20时质量矩计算误差Fig.6 L/D=20, mass momentof inertia calculation error

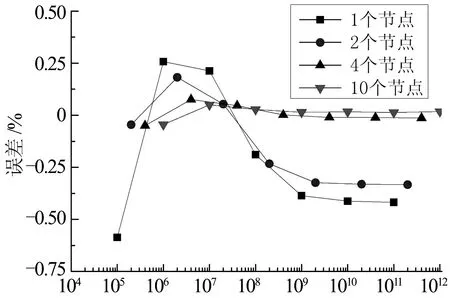
附加质量矩/(kg·m2)图7 L/D=55时质量矩计算误差Fig.7 L/D=55, mass momentof inertia calculation error

由图5-图7可知：

1)就钢桁梁的长细比L/D而言，随着长细比的增加，质量矩计算误差减小.当L/D=20，附加质量矩采用4节点或10节点加载时，质量矩计算误差在3%以内；当L/D=55，附加质量矩采用4节点或10节点加载时，质量矩计算误差在0.1%以内.

2)就附加质量矩施加位置而言，4节点、10节点加载与1节点、2节点加载相比，质量矩计算误差更小，即上下弦杆加载或全截面加载时，质量矩计算误差更小.

下面从力学角度对以上2种因素进行简要分析.在简化算法的推导过程中，得到一个结论：质量矩均匀分布的悬臂梁模型在附加质量矩前后，结构的一阶扭转振型不变.然而对于钢桁梁悬臂结构，这个结论很难严格成立.

当悬臂钢桁梁长细比较小时(L/D=10)，无论附加质量矩在何处加载，质量矩计算误差均较大.原因是悬臂钢桁梁的长细比较小，其在扭转时会发生翘曲，造成同一横截面各节点扭转角有明显差异，平截面假定不再满足，故附加质量矩前后，很难保证它的一阶扭转振型严格不变.

未附加质量矩时，悬臂钢桁梁的刚度、质量分布较合理，其一阶扭转振型为桁架断面整体的扭转变形，不会发生局部变形.附加质量矩后，结构刚度不变，质量分布发生变化.对于工况一和工况二，附加质量矩施加的位置处刚度比较小，可能导致结构一阶扭转时发生局部变形，从而造成较大的计算误差.对于工况三，附加质量矩施加的位置处刚度比较大，结构一阶扭转振型没有局部变形.对于工况四，横断面各节点均附加质量矩，同一断面内质量分布均匀变化，结构的一阶扭转振型没有局部变形.

3.4 一阶扭转频率对比

理论上，若悬臂钢桁梁与悬臂单主梁满足刚度、质量(矩)、边界条件等效，则两者的频率等动力特性参数应该基本相同.

这里，钢桁梁长细比取L/D=55，附加质量矩采用全截面加载.建立悬臂单主梁模型时，各节段(节段长度为8.4 m)质量矩大小仍取为4.028×107kg·m2，计算得到钢桁梁竖向、侧向的惯性矩分别为11.8 m4和230 m4，扭转惯性矩为11.1 m4，计算不同的附加质量矩下悬臂钢桁梁和悬臂单主梁的一阶扭转频率，计算结果见表4.这里，ΔIm表示钢桁梁各节段的附加质量矩大小，f桁表示悬臂钢桁梁的一阶扭转频率，f单表示悬臂单主梁的一阶扭转频率.

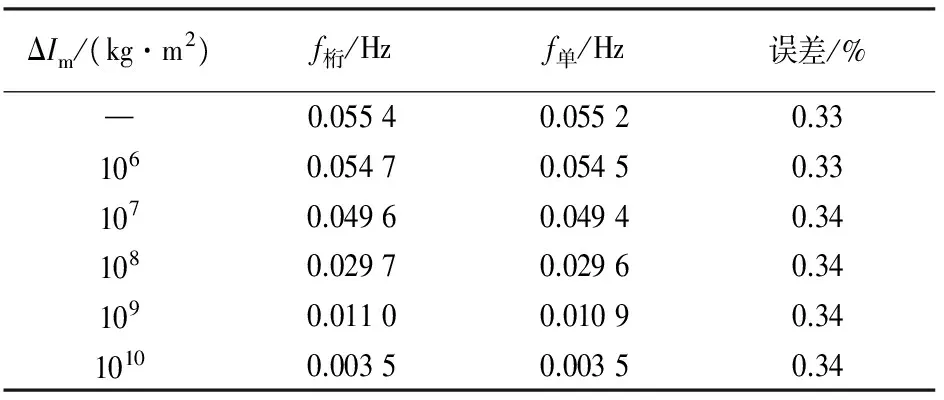
表4 悬臂钢桁梁与悬臂单主梁一阶扭转频率对比Tab.4 Comparison of 1st torsion frequency between the cantilever of stiffening truss and the cantilever of single girder

需要说明的是，第一，质量矩只影响扭转有关频率及振型，因此实际建模时，不需要沿梁长限制各节段的竖向和侧向自由度，只需找到悬臂梁的一阶扭转频率.第二，附加质量矩不可太小或太大，若太小，附加质量矩前后结构频率变化甚微，则公式(12)可能会造成较大的计算误差；若太大，则可能导致质量矩阵出现畸变，从而难以求解特征值．

4 工程应用实例

常见的大跨度悬索桥的钢桁梁，各杆件截面沿梁跨变化不大，其质量分布沿梁长可近似看作均匀分布，满足该方法的适用条件.本文以洞庭湖二桥和矮寨大桥为例，来验证该方法的有效性.

洞庭湖二桥为主跨为1 480 m的双塔双跨钢桁架悬索桥，桥跨布置为(1 480+453.6) m，主梁全长为1 933.6 m.主桥主缆的孔径布置为(460+ 1480+491) m，主缆垂垮比F/L=1/10，主索中心距为35.4 m，采用平面索布置.主梁是钢桁梁，其有关信息与上面数值仿真分析中的钢桁梁相同；主塔为门式框架桥塔，两岸锚碇为重力式锚碇.矮寨大桥为主跨为1 176 m的单跨钢桁架悬索桥，有关该桥的详细信息可参见文献[12]，这里不再详述.

计算钢桁梁质量矩时，为减小计算误差，采用全截面加载，悬臂梁跨度取原桥主梁全长，所使用单元类型与上文数值仿真分析中相同.所不同的是钢桁架各杆件及桥面板的质量矩不再采用mass21单元施加，而是按实际密度加以考虑，计算结果见表5.这里，ΔIm表示节间长度的桁梁所附加质量矩大小(洞庭湖二桥主梁、矮寨大桥主梁的节间长度分别为8.4 m，7.25 m)，fi表示悬臂钢桁梁的一阶扭转频率，Im表示节间长度的钢桁梁质量矩大小.需要说明的是，这里已验证了附加质量矩前后，悬臂钢桁梁的一阶扭转振型未发生改变.这里给出了洞庭湖二桥加劲梁的悬臂梁模型在附加质量矩前后的一阶扭转振型图(图8).

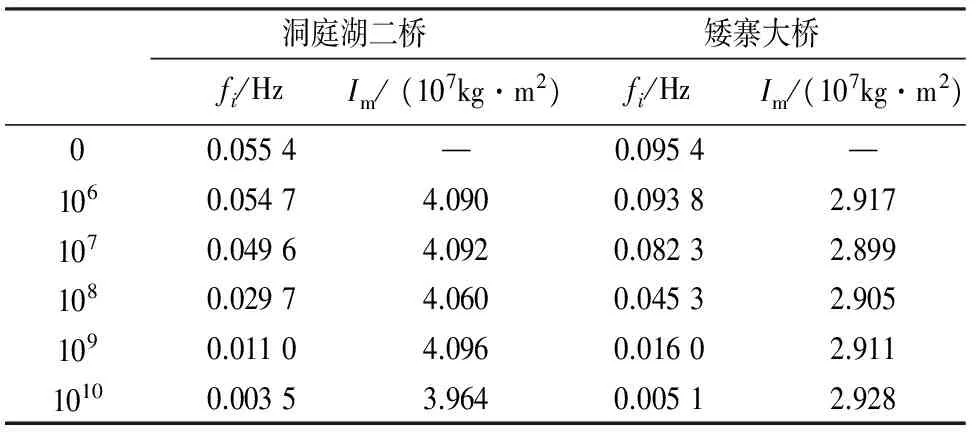
表5 不同附加质量矩所计算的质量矩大小Tab.5 Mass moment of inertia calculation results with different additional mass moment of inertia

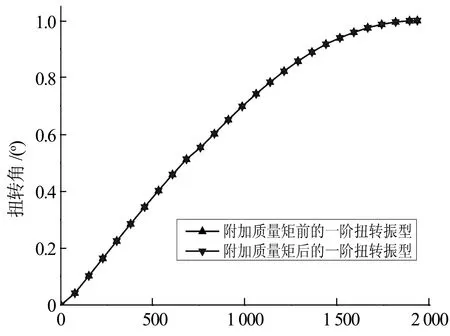
跨度/m图8 附加质量矩前后结构的一阶扭转振型Fig.8 Comparison of the 1st torsional mode shape whether with additional mass moment of inertia or not

理论上，悬索桥的全桁架模型和单主梁模型两者计算的结构动力特性基本上是一样的.为验证该方法计算得到的质量矩的正确性，单主梁模型中的质量矩参数采用该方法计算得到的数值，计算扭转相关频率，并与全桁架模型的计算结果对比，见表6.由表6知，本文方法计算得到的质量矩准确度高.

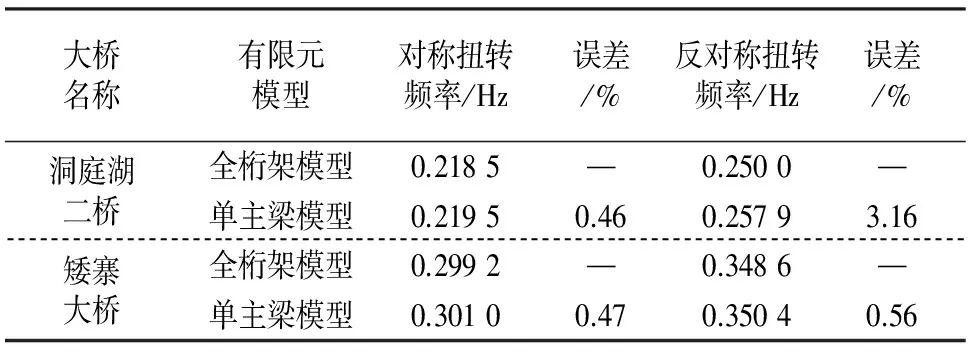
表6 全桁架模型和单主梁模型扭转有关频率对比Tab.6 Comparison of torsion related frequency between full truss model and single spine girder model

5 结 论

本文讨论了一种基于附加质量矩前后结构动力特性的变化计算钢桁梁质量矩的方法.

数值仿真结果表明：1)钢桁梁的长细比L/D对质量矩的计算有较显著的影响，L/D≥20时，该方法计算的质量矩有较高的精度.对于钢桁梁简支梁，其长细比L/D一般小于20，故此方法对计算钢桁梁简支梁的质量矩有局限性.2)附加质量矩的施加位置对质量矩的计算结果有较显著影响，当附加质量矩均匀附加在全截面或上、下弦杆时计算精度更高.此外，附加质量矩时，沿梁跨方向，要保证在钢桁梁各节段处均匀附加扭转质量单元；沿横断面方向，要保证附加扭转质量单元左右对称分布.

采用该方法分别得到了洞庭湖二桥和矮寨大桥加劲梁的质量矩，并将该参数应用到单主梁模型中，计算了洞庭湖二桥的动力特性，并与全桁架模型的计算结果进行了对比.结果表明，两者扭转相关频率基本相等，验证了该方法的有效性.

[1] 刘正光.香港青马大桥的设计[J].土木工程学报，1992,25(5):77-80.

LIU Zhengguang. The design of Qingma Bridges in HongKong[J]. China Civil Engineering Journal, 1992,25(5):77-80.(In Chinese)

[2] TANAKA H , DAVENPORT A G. Wind-induced response of Golden Gate Bridge[J]. Journal of Engineering Mechanics, 1983,109(1): 296-312.

[3] KITAGAWA M. Technology of the Akashi Strait Bridge [J]. Structural Control and Health Monitoring, 2004,11(2)：75-90.

[4] 胡峰强.山区风特性参数及钢桁架悬索桥颤振稳定性研究[D].上海：同济大学土木工程学院,2006:68-90.

HU Fengqiang. The research of wind characteristic parameters and flutter instability of suspension bridges with a steel truss stiffened girder in mountainous regions[D]. Shanghai: College of Civil Engineering, Tongji University, 2006:68-90. (In Chinese)

[5] 于永帅.钢桁架悬索桥抖振响应及其影响参数分析[D].长沙：湖南大学土木工程学院,2011:14-20.

YU Yongshuai. Buffeting response of steel truss girder suspension bridge and influence parameters investigation[D]. Changsha: College of Civil Engineering, Hunan University, 2011:14-20. (In Chinese)

[6] NAMINI A, ALBRECHT P, BOSCH H. Finite element-based flutter analysis of cable-suspended bridges[J]. Journal of Structural Engineering, 1992, 118(6):1509-1525.

[7] 苏成.大跨度斜拉桥三维有限元动力模型的建立[J].华南理工大学学报，1999,27(11):51-56.

SU Cheng. The established 3-D element finite dynamic models for long-span cable-stayed bridges[J]. Journal of South China University of Technology, 1999,27(11):51-56.(In Chinese)

[8] 刘志文,洪涵,梁立农,等. 广东江顺大桥的抗风性能试验研究[J]. 湖南大学学报：自然科学版,2015，42(3): 112-119.

LIU Zhiwen, HONG Han, LIANG Linong,etal. Experimental investigation of wind-resistant performance of Jiangshun Bridge in Guangdong [J]. Journal of Hunan University: Natural Sciences, 2015, 42(3): 112-119.(In Chinese)

[9] 范立础.桥梁抗震[M].上海:同济大学出版社，1997:118-121.

FAN Lichu. Aseismic of bridges[M]. Shanghai: Tongji University Press, 1997:118-121. (In Chinese)

[10]王浩,李爱群,郭彤，等.带中央扣的超大跨度悬索桥多尺度有限元模拟方法[J].中国公路学报,2009,22(6):60-66.

WANG Hao, LI Aiqun, GUO Tong,etal. Multi-scale finite element modeling method on super-long-span suspension bridges with central bucle[J]. China Journal of Highway and Transport, 2009, 22(6): 60-66.(In Chinese)

[11]R W 克拉夫.结构动力学[M].北京:高等教育出版社，1997:160-171.

CLOUGH R W.Structural dynamics[M].Beijing: Higher Education Press，1997:160-171. (In Chinese)

[12]HU Jianhua, CUI Jianfeng. Innovative techniques of design of Aizhai Bridge in West Hunan[J]. Bridge Construction, 2011,31(6):54-61.

of Inertia of Stiffening Truss in Suspension Bridges

HUA Xugang†, YANG Kun, WEN Qing, CHEN Zhengqing

(Key Laboratory for Wind and Bridge Engineering of Hunan Province, Hunan University, Changsha 410082, China)

The simplified “fish-bone” model is commonly employed for the analysis of wind-induced responses of truss-stiffened suspension bridges, and one key step in establishing such a model is the calculation of the mass moment of inertia for the stiffening truss. Due to numerous members in a stiffening truss section, the calculation process of the moment of inertia is usually complicated and imprecise. Therefore, a new method is proposed based on the change in torsional frequencies of a cantilever truss girder caused by attaching the additional mass moment of inertia on the truss nodes, where the theoretical background is given, and the applicable conditions are also investigated. By taking a cantilever truss girder as an example, numerical simulation results show that the proposed method provides the best accuracy when the known mass moment of inertia is uniformly applied to all section nodes or to the nodes of chord joints, and the slenderness ratio of truss girder exceeds 20. Finally, the mass moments of inertia of stiffening truss are obtained by the proposed method, and are then used to establish the simplified “fish-bone” models for several selected suspension bridges. The torsional frequencies obtained by the simplified “fish-bone” models agree well with those predicted by their detailed models, which validates the effectiveness of this simplified method.

stiffening truss; suspension bridges; mass moment of inertia; wind-resistant design

2016-03-02

国家自然科学基金资助项目(51278189),National Natural Science Foundation of China(51278189)；国家优秀青年基金资助项目(51422806)，National Outstanding Youth Science Foundation(51422806);交通运输部建设科技项目(2013318798320)，Construction Science and Techndogy Project by MOT(2013318798320)

华旭刚(1978-)，男，浙江义乌人，湖南大学教授，博士生导师 †通讯联系人，E-mail:cexghua@hotmail.com

1674-2974(2017)03-0001-07

10．16339/j．cnki．hdxbzkb．2017．03．001

U448.25

AA Simplified Method for Calculating Mass Moment