在活动化生本课堂中生成数学活动经验
【摘要】“活动化”教学强调让学生充分经历知识生成、发展的过程,课堂必须利于学生基本数学活动经验积累,强调在“以学生发展为根本”的生本教育理念引导下,发挥学生课堂学习的主观能动性,让学生最大限度发挥潜能、施展才华、主动汲取。教师可以从数学工具的形成过程、知识前后的链接过程、策略的建构过程这三方面入手设计数学活动。
【关键词】活动化;生本课堂;策略
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2017)17-0072-02
【作者简介】潘剑,江苏省镇江市丹徒区辛丰中心小学(江苏镇江,212100)教师,一级教师。
《义务教育数学课程标准(2011年版)》将数学活动经验提到了一个前所未有的高度,其在课程目标中被进一步明确,地位进一步得到凸显。如何认识数学活动经验,如何在教学中落实使学生获得数学活动经验这一目标,成为我们必须面对的新课题。
一、活动化生本课堂的基本理念
“活动化”教学强调让学生充分经历知识生成、发展的过程,课堂教学必须有利于学生基本数学活动经验积累,强调在“以学生发展为根本”的生本教育理念引导下,发挥学生课堂学习的主观能动性,让学生最大限度发挥潜能、施展才华、主动汲取。要求教师能针对各类知识的特点,在尊重知识生长规律和学生学习特点基础上,精心设计和开展数学活动,使知识能真正进入学生的视界,激起学生主动介入的欲望,使他们乐于在活动中接受、探究和感悟知识。
学习是一个意义建构的过程,经验是构建学习的基本元素,基础知识、基本技能需要通过经验的转化才能升华成学生的素养,经验的积淀和发展是课程与教学追求的目标之一。活动经验的生成和积累离不开数学活动,学生只有经历了观察、比较、实验、猜想、操作、验证等活动,才能累积起丰富的经验。
二、活动化生本课堂活动经验生成策略
“数学应根据具体的教学内容,注意使学生在获得间接经验的同时,也能够有机会获得直接经验。”教师要精心设计数学活动,引导学生主动参与其中,让学生在经历“玩”数学的活动之余理性思考,将个人“经历”升华成宝贵“经验”。可以从以下三方面入手设计活动化教学,促进学生活动经验的生成。
1.经历数学工具的形成过程。
精心设计活动教学,模拟工具产生需求的情境,让学生经历工具的生成过程,体验工具的构造原理及操作特点,这样的设计更利于学生接受、理解知识,并积累丰富的学习经验。
在教学苏教版二上《认识厘米》时,笔者设计了体验直尺工具形成的活动,教学实录如下:
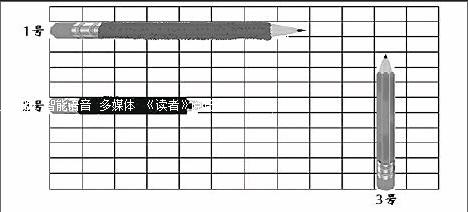
师:(如图)说一说每支铅笔的长度各占几格?
生:1号铅笔长8格,2号铅笔长5格,3号铅笔长8格。
师:1号铅笔和2号铅笔比,谁长一些?你是怎么想的?
生:1号铅笔长8格,2号铅笔长5格,1号铅笔比2号长。
师:1号铅笔和3号铅笔比,谁长?
生:1号铅笔长。
师:1号铅笔长8格,3号铅笔也长8格,为什么1号却比3号长呢?
生:因为每格长度不一样长。
师:我们用同样的格子长度来度量,便于比较物体的长短。如果没有这样的格子图可以怎样比较?
学生讨论后汇报:用统一的小段去度量。
师:为了度量方便,人们还将这些相等的小段拼接在一起,后来人们又把这种固定长度刻在笔直的木条上就逐渐形成了尺。
接着认识1厘米和几厘米,学会用厘米测量物体的长度。在教学活动中,学生经历了直尺的产生过程,清楚了直尺的测量原理,积累了数学活动经验,为后续《认识毫米》积蓄了认知基础和实践经验。
2.经历知识前后的链接过程。
数学知识学习是一个循序渐进、螺旋上升的过程,通过对简单的直观活动经验进行提升,以形成新的活动经验,促使学生的经验从一个水平上升到更高的水平。
以平面图形的面积教学为例,长方形、正方形的面积探究经验最早来自于长度测量的经验,看看一条线段中有几个固定长度单位,它的长度就是几。在学习苏教版三下《长方形和正方形的面积》时,也是沿用此法,只不过要考虑两个维度里能容纳的单位面积正方形,从而计算出一共能容纳的单位面积正方形的个数,得出它的面积,进而获得长方形面积计算公式。积累长方形面积计算经验,学生的活动经验得到第一次生长。随后学习“平行四边形的面积”时,学生通过图形的转化,在长方形和平行四边形之间架起了桥梁,主动将长方形面积计算经验迁移到平行四边形的面积计算中来。学生的认知活动经验得以升华,不但巩固了平行四边形面积计算的直接经验,还将“转化”的数学思想植根心中。同样,在后来学习三角形、梯形时学生不断调用这些活动经验和思想方法。
3.经历策略的建构过程。
数学来源于生活,许多解决问题的策略都是从实际生活的经验中提取凝炼而成,因此在数学策略教学中,我们应以生活的經验为起点,充分调用学生的经验,精心设计数学活动,将学生的生活经验转化为数学经验,积累探究、操作、建立数学模型的经验。解决问题活动的价值不局限于获得具体问题的结论和答案,它的意义更在于使学生学会解决问题,体会自己对问题的理解,在实践和创新的过程中获得最具数学本质和价值的数学活动经验。
例如在教学《解决问题的策略》时,可以设计生活中的换购情境。
师:小军的妈妈买了10支铅笔,小军想把它们换成圆珠笔,你能帮帮他吗?他需要到商场了解哪些信息?
生1:要了解铅笔和圆珠笔的单价。
生2:找到铅笔和圆珠笔单价之间的关系。
师:如果圆珠笔的单价是铅笔的2倍,可以怎样换?
生:用2支铅笔可以换回1支圆珠笔,10支铅笔一共可以换回5支圆珠笔。
师:如果圆珠笔的单价比铅笔贵0.5元,可以怎样换?
生:用1支铅笔换回1支圆珠笔要补交0.5元,10支铅笔全部换成圆珠笔一共要补交5元。
师:第一种情况下为什么要用2支铅笔才能换回1支圆珠笔,第二种情况下为什么用1支铅笔换回1支圆珠笔还要补交0.5元?
生:第一种是因为2支铅笔的价钱等于1支圆珠笔的钱,第二种是因为1支铅笔价格+0.5元=1支圆珠笔价格。
师:这种方法叫等价交换,今天我们就要用这种方法来解决问题。
教学要从经验出发,通过换购经历,让学生初步感受替换的数学思想,然后应用换购经验解决问题,让学生经历替换操作的全过程,并将经验提升为解决此类问题的通用方法和策略。
总之,数学活动化教学是将学生的数学经历转化成数学经验的有效途径,教学时要重视引导学生经历数学知识方法获得的过程,教师要注重学生经历数学活动后的反思过程,通过反思不断提升数学活动的经验。

