基于复杂网络的社交网络用户影响力研究

徐杰，王菊韵，张海云

(1.中国传媒大学 理学院，北京100024；2.北京化工大学 信息科学与技术学院，北京100029)

基于复杂网络的社交网络用户影响力研究

徐杰1，2，王菊韵1，张海云1

(1.中国传媒大学 理学院，北京100024；2.北京化工大学 信息科学与技术学院，北京100029)

基于复杂网络理论对社交网络用户影响力进行分析，可以为社会营销、舆情监测、信息检索等众多领域的研究提供支持。传统的网页排序算法虽然可以对有向社交网络的用户影响力进行分析，但仍存在缺陷且复杂度较高。本文提出了一种对无向社交网络进行用户影响力评价的方法，弱化了将有向网络视为无向网络研究而带来的误差，并可以高效地得到重要节点，适用范围更广。首先，本文采用网络节点的度中心性、介数中心性、接近中心性、聚类系数作为节点重要度评价指标，通过对计算数据归一化处理并取均值得到用户影响力排序的基准。其次，采用k-核分解法粗粒化地将重要度相似的节点进行归类，来检验排序的合理性。最后，通过仿真实验以及k-核分解、与HITS算法比较验证了此方法的科学性和正确性。

社交网络；用户影响力；网络节点重要度；k-核分解

1 引言

复杂网络的相关研究已经成为多个学科共同关注的前沿热点。随着各种在线社交网络不断涌现，大量具有研究价值的网络数据应运而生。对社交网络用户影响力进行分析，可以为社会营销、舆情监测、信息检索等众多领域的研究提供支持。此研究已成为一个新兴且热门的研究课题。

针对不同类型的网络和不同的研究问题，节点的重要性判断标准也不同，在线社会网络用户的重要性刻画方法也多种多样。其中最为常用的方法为Kleinberg提出的HITS算法[1]、Page和Brin提出的PageRank算法[2]两种网页排序算法以及对其进行改进的算法。HITS和PageRank算法在20世纪90年代后期几乎同时提出，后成为搜索引擎领域中的网页重要度排序的经典算法。任晓龙等人的《网络重要节点排序方法综述》[3]与兆云等人的《社交网络影响力研究综述》[4]对两种算法进行了详细的介绍与分析。后来通过各种各样的方法将社交网络数据抽象成有向网络模型，网页排序算法开始被用于社交网络的研究。代表性的研究工作有Song等人[5]考虑博文新颖度提出的InfluenceRank算法。Haveliwala等人[6]考虑了用户之间的链接与主题内容，运用PageRank思想对用户影响力进行了研究。Zhongwu Zhai 等人[7]基于正向有权网络假设，发现了一种基于兴趣的PageRank算法来识别重要用户。Meeyoung Cha[8]通过研究用户行为与影响力之间的关系，以及与斯皮尔曼等级相关系数比较来得出用户影响力排名。Shaozhi Ye[9]通过分析Twitter的用户行为与粉丝数量、推文的响应数，提出了一种将用户主页内容作为重要度排序指标的方法。但网页排序算法仍存在缺陷且复杂度高。算法的收敛性和有效性不能同时保证，并且通常只适用于特定类型的社交网络。针对这些问题，本文提出了一种直接对无向社交网络进行用户影响力评价的方法，弱化了将有向网络视为无向网络研究而带来的误差，并且可以高效地得到重要用户节点，适用范围更广。

2 四指标综合用户影响力评价方法

20世纪90年代，HITS首次用不同指标(权威值和枢纽值)同时对网络中的节点进行排序，本研究综合了网络节点的度中心性、介数中心性、接近中心性、聚类系数等四个指标对无向网络节点重要度进行评价的方法。该方法如图1所示，首先按照一定规则建立社交网络模型，并对网络节点的四个指标进行计算。其次，对四个指标的计算结果分别进行归一化处理，消除指标之间的量纲影响。然后，对归一化后的四个指标取均值，均值即为用户影响力排序的基准，根据均值的大小比较得到最终用户影响力排序。最后，运用k-核分解法对排序结果进行检验。

图1 四指标综合用户影响力评价方法示意图

3 仿真实验与结果分析

3.1 数据来源及模型构建

本文使用的数据来源于http：//lovro.lpt.fri.uni-lj.si/，此主页为卢布尔雅那学者lovrosubelj对网络科学方面研究内容的共享的开发数据。所使用的建模及计算工具为大型复杂网络分析软件Pajek。

对于大型复杂网络的研究通常先需要对大型网络分解成社区或团体等规模相对较小的网络，以便进行研究。本文选用Facebook用户slavko的好友圈数据，根据slavko的好友圈中用户之间的好友关系建立无向网络。无向网络模型中共包含334个用户节点，2218条边。为了方便表示，将用户节点分别标记为v1，v2，……，v334。建立的无向网络模型如图2所示。

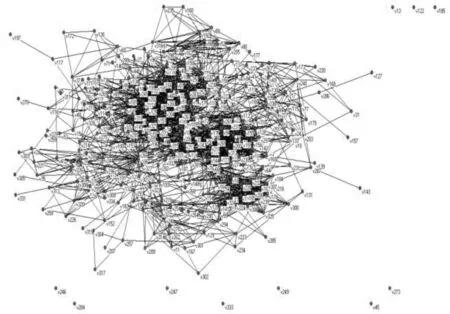
图2 slavko的好友关系网络

该网络模型能够直观地描述网络的1阶度分布信息，即网络中不同度的节点各自所占的比例。但是，具有相同度分布的两个网络可能具有非常不同的其他性质或行为，还需要考虑包含更多结构信息的高阶拓扑特性来刻画网络，如网络的度相关性及同配性(2阶度分布特性)。大量的实证研究表明，不同的在线社会网络可以呈现不同的同配、异配或接近中性的特征。根据Ugander J等人的研究，含有7亿多个节点的Facebook网络呈现出同配性，r=0.226[11]。经计算，本文所建网络模型的同配系数r=0.2473，大于0，也呈现出同配性。因此，此网络模型能够较好地刻画该团体网络用户之间的好友关系。

3.2 用户影响力分析

3.2.1 度中心性研究

在社会关系网络中，位置越中心的节点其价值越大，最直接的度量就是度中心性，一个包含N个节点的网络中，度为的节点的度中心性值定义为：

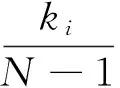
(1)

基于Pajek计算得到各用户节点(UserID)的度中性值(DegreeCentrality)，如图3所示。

图3 各节点的度中心性值

表1给出了网络中度中心性排名前10的用户节点及其对应的度中心性值和数据归一化处理后的取值。表中数据采用min-max归一化(后面各指标的计算也均采用此方法)，转换函数如下：

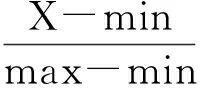
(2)

其中max为样本数据的最大值，min为样本数据的最小值。

整个网络中度中心性最大值为0.174174，最小值为0。

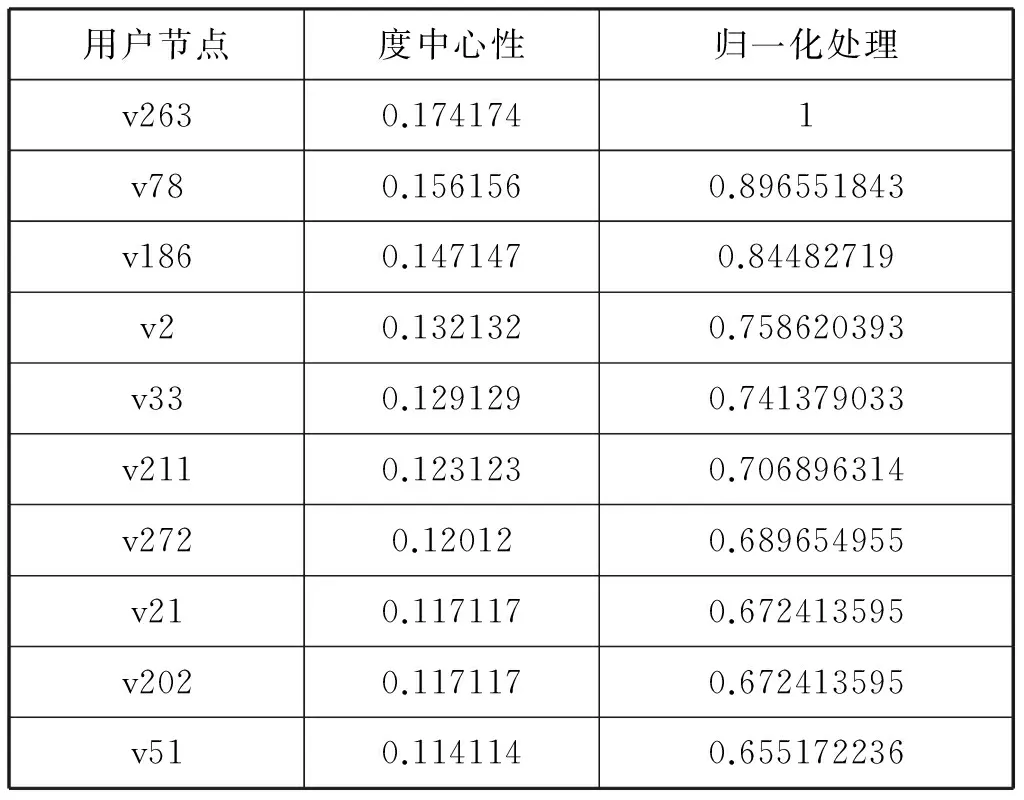
表1 度中心性值排名前10的节点

3.2.2 介数中心性研究

度中心性虽然能直观的描述节点的重要度，但很容易忽视网络中一些在控制信息传输上起着重要作用的节点。例如，一个连接2个较大子网的节点，其本身的度值虽然不高，但在两个子网的信息传输上却却承受了较大的信息流量。节点i的介数定义为：

(3)

基于Pajek计算得到各用户节点(User ID)的介数(Betweenness centrality)，如图4所示。

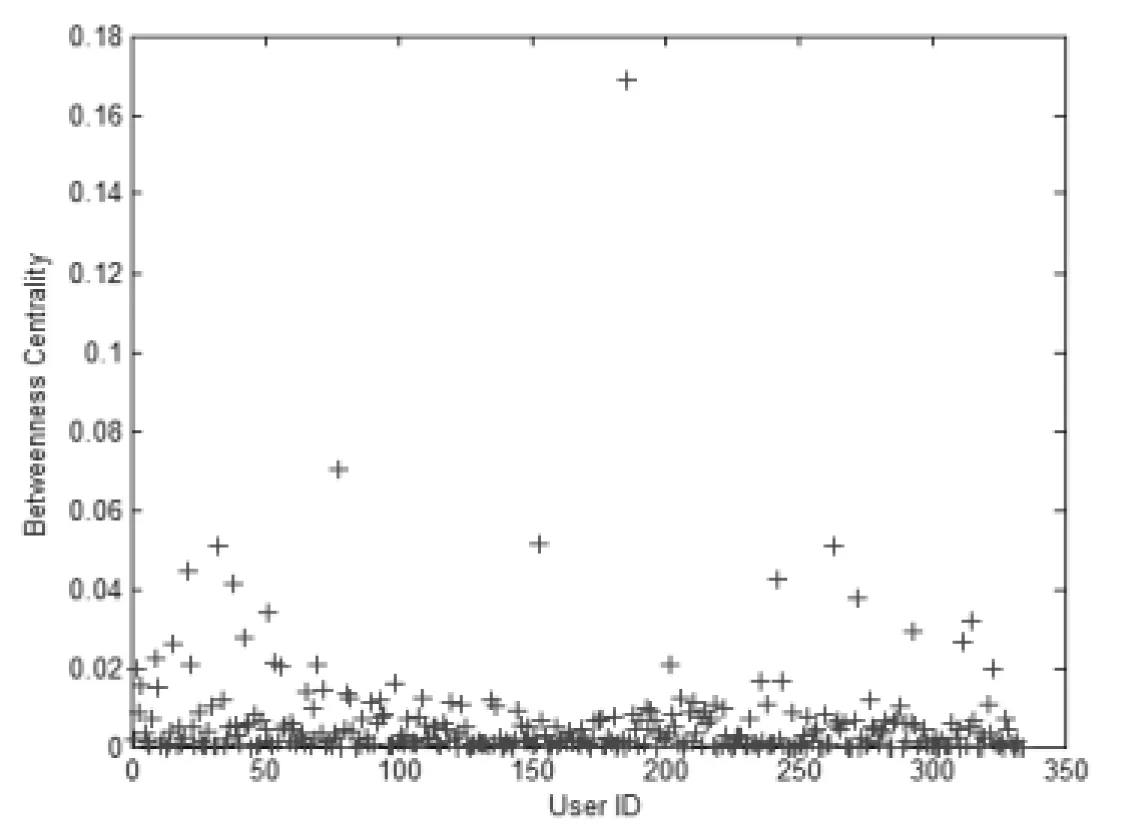
图4 各节点的介数中心性值

表2给出了网络中介数中心性排名前10的用户节点及其对应的介数取值和数据归一化处理后的取值。整个网络中，介数最大值为0.16854，最小值为0。介数越大的用户节点，在整个网络的最短路径中所占数目越多。

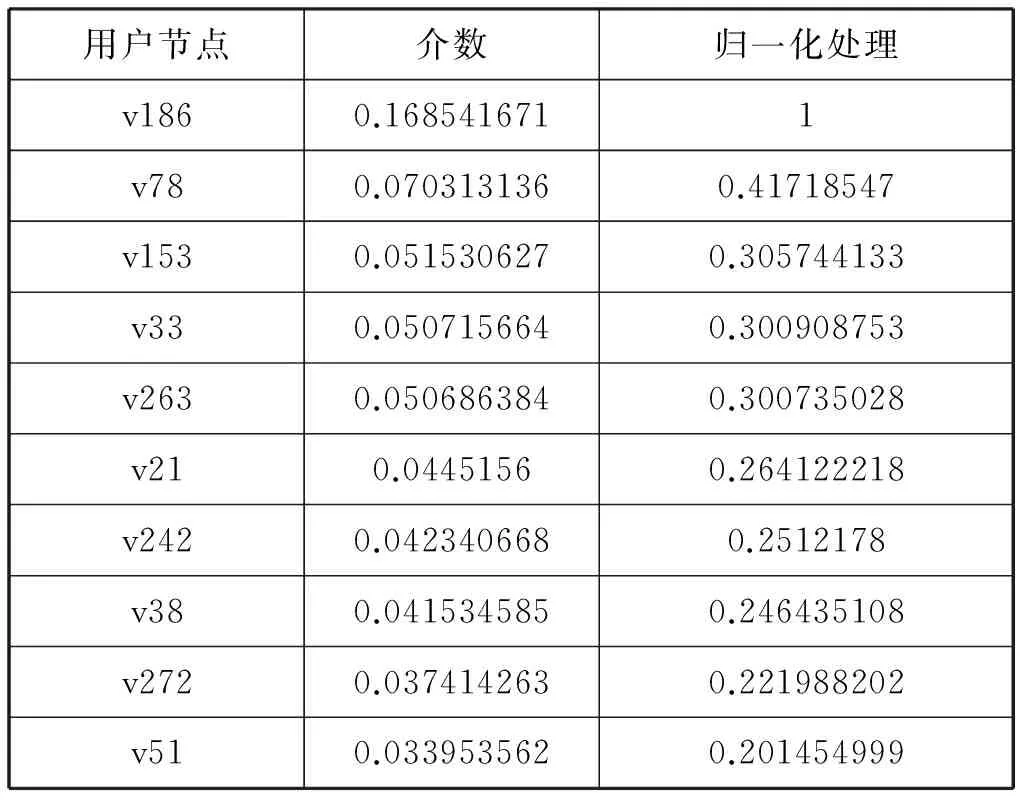
表2 介数排名前10的节点

3.2.3 接近中心性研究

无权网络中，最短路径上节点数目的多少对网络中信息的传输效率是有影响的，一个含有N个节点的网络中的节点i的接近数定义为

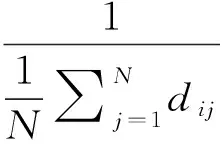
(4)

其中，dij是节点i到节点j的距离。

接近数与介数一样，都考虑到了整个网络中任意两个节点之间的最短路径，但是，接近数最大的节点表示信息的流动具有最佳的观察视野。一般而言，介数最大的节点并不一定就是接近数最大的节点。就社交网络而言，一个用户节点的接近数越大，其在整个网络中信息能够传播的视野范围也就越大，影响力也就越大，反之，影响力越小。

基于Pajek计算得到各用户节点(UserID)的接近数(Closenesscentrality)，如图5所示。

图5 各节点的接近中心值

表3给出了网络中接近中心性排名前10的用户节点及其对应的接近数取值和数据归一化处理后的取值。整个网络中接近数的最大值为0.447613，最小值为0。

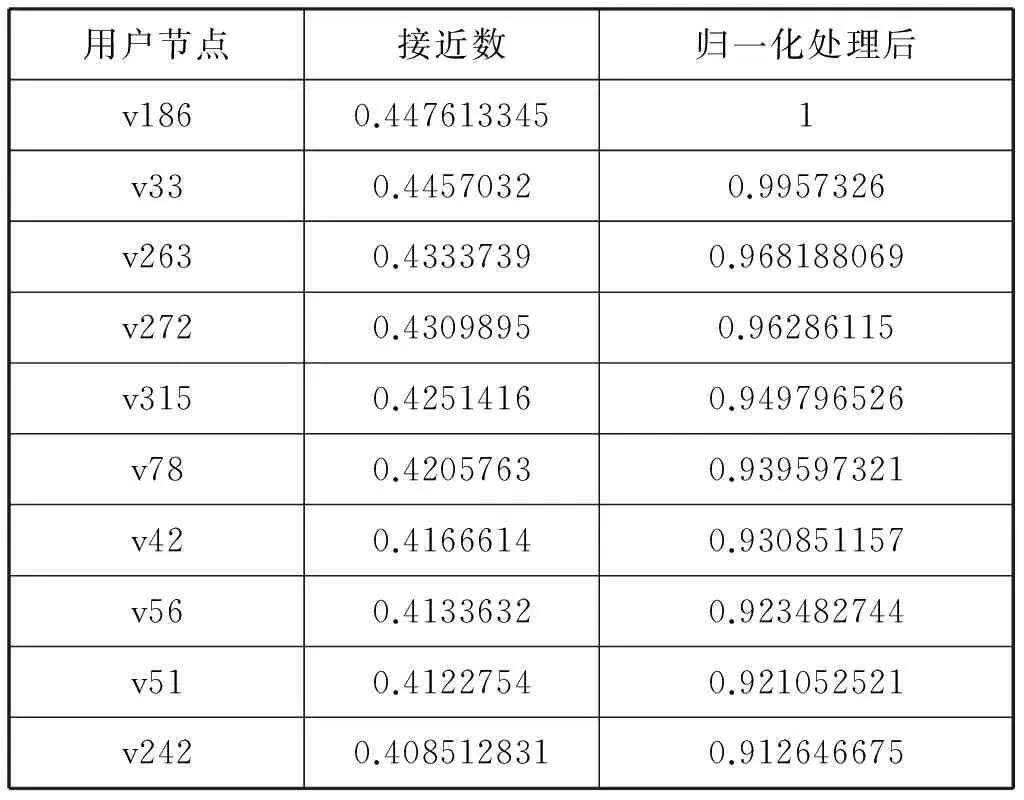
表3 接近数排名前30的节点

3.2.4 聚类系数研究

聚类系数可以定量刻画社交网络中一个人的任意两个朋友之间也互为朋友的概率。这种可能性的大小反映了这个人的朋友圈的紧密程度。网络中一个度为ki的节点i的聚类系数定义为

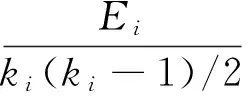
(5)

其中，Ei是节点i的Ei个邻节点之间实际存在的边数。在现实的网络中，尤其是在特定的网络中，由于相对高密度连接点的关系，节点总是趋向于建立一组严密的组织关系。这种相互关系可以利用聚类系数进行量化表示。聚类系数越大，其所在局部网络的凝聚力越大，影响力也相对较大，反之，影响力越小。而这些节点通常并非是度值、介数、接近数较高的节点。

基于pajek计算得到各用户节点(UserID)的聚类系数值(Clusteringcoefficient)，如图6所示。表4给出了网络中聚类系数排名前30的用户节点及其对应的聚类系数值和数据归一化处理后的取值。整个网络中聚类系数的最大值为1，最小值为0。在一定时间内，用户之间的关系是可能发生变化的，可以随时取消或添加好友，而聚类系数较大的节点，在一定时间内，周围节点对其取消关注的概率相对较小，周围节点对其添加关注的概率相对较大。

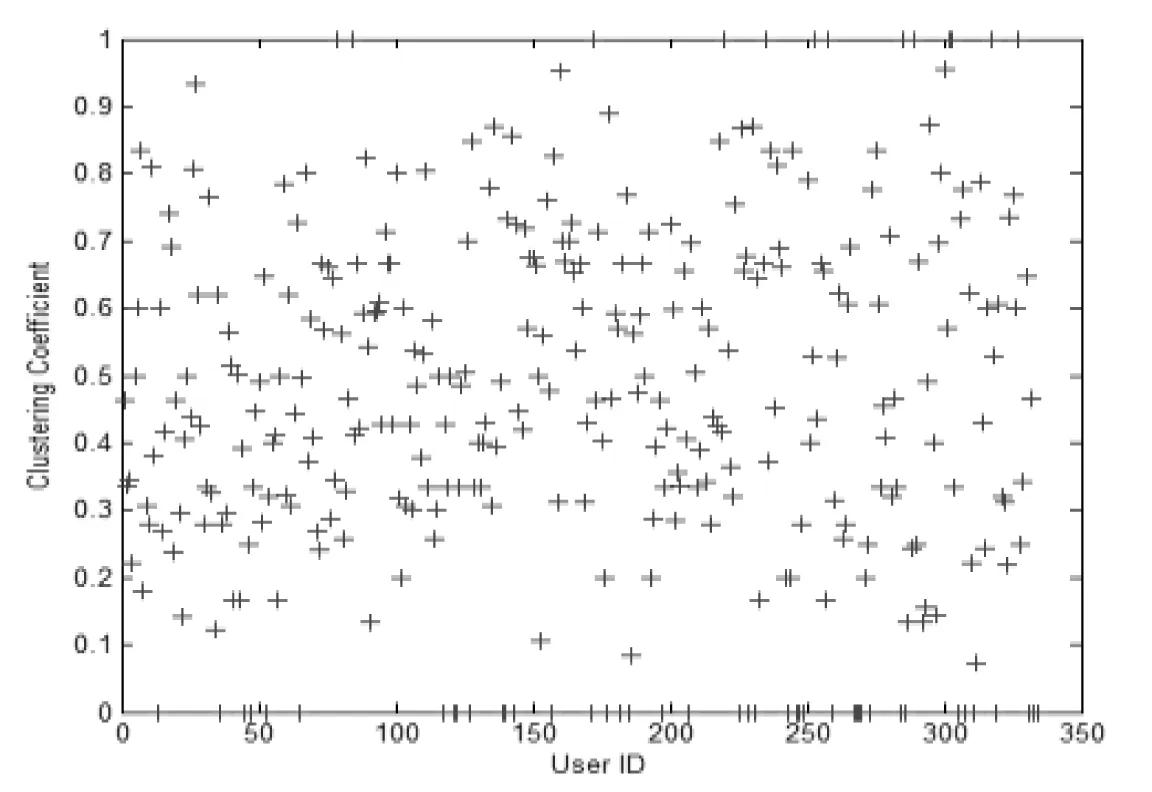
图6 各节点的聚类系数值

表4 聚类系数排名前30的节点

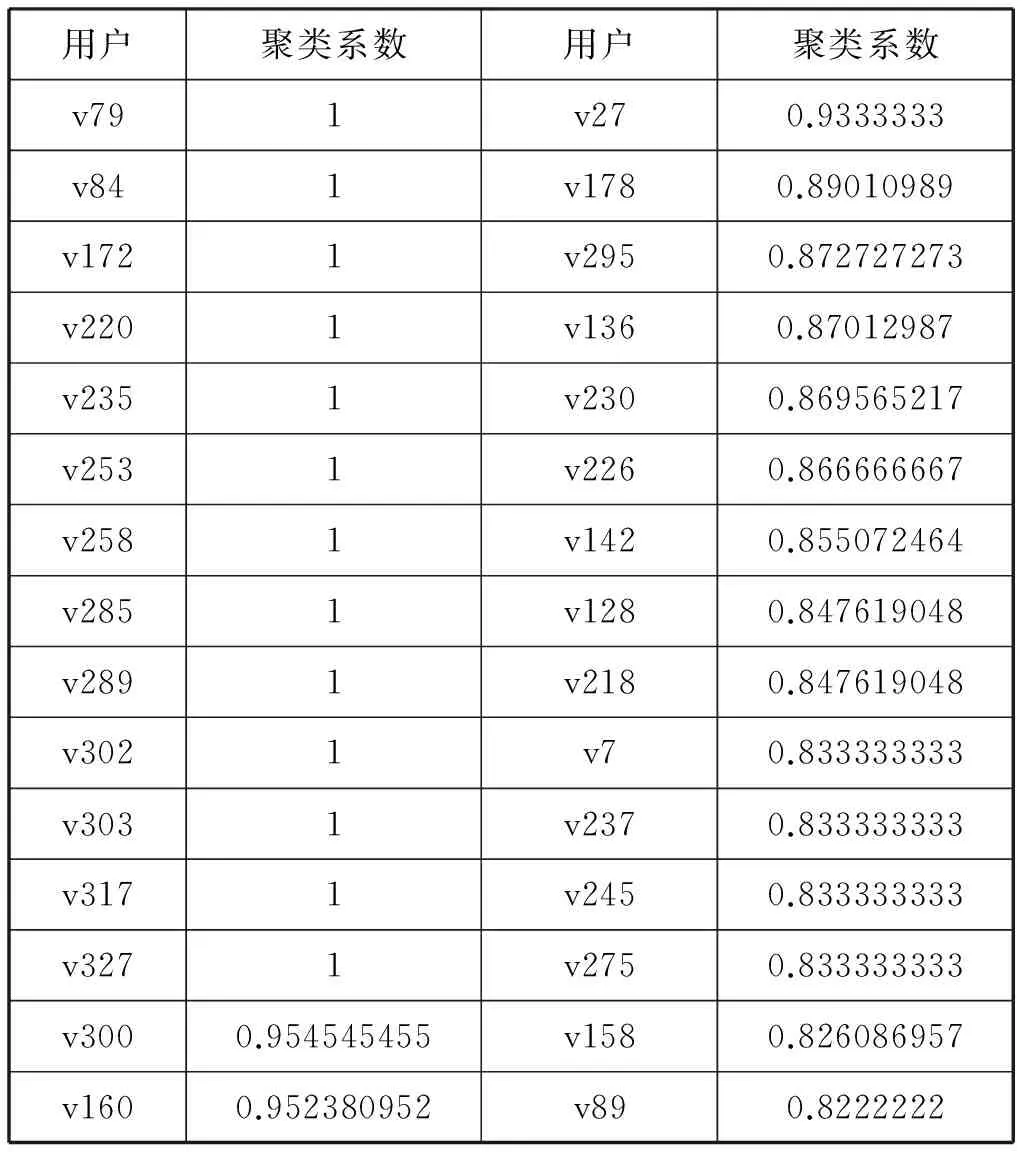
用户聚类系数用户聚类系数v791v270.9333333v841v1780.89010989v1721v2950.872727273v2201v1360.87012987v2351v2300.869565217v2531v2260.866666667v2581v1420.855072464v2851v1280.847619048v2891v2180.847619048v3021v70.833333333v3031v2370.833333333v3171v2450.833333333v3271v2750.833333333v3000.954545455v1580.826086957v1600.952380952v890.8222222

3.2.5 用户影响力排序

用户影响力指标为四个指标归一化后所取均值，均值大小即代表影响力大小，记为Ai，计算公式为

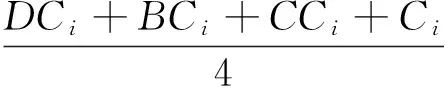
(6)

其中，DCi，BCi，CCi，Ci分别为度中心性值、介数、接近数、聚类系数归一化后的取值。图7给出了所有用户节点(UserID)及其对应的均值(AverageValue)。结果显示，v186，v78，v263，v33，v42，v21等用户节点在整个网络中的影响力是比较大的。

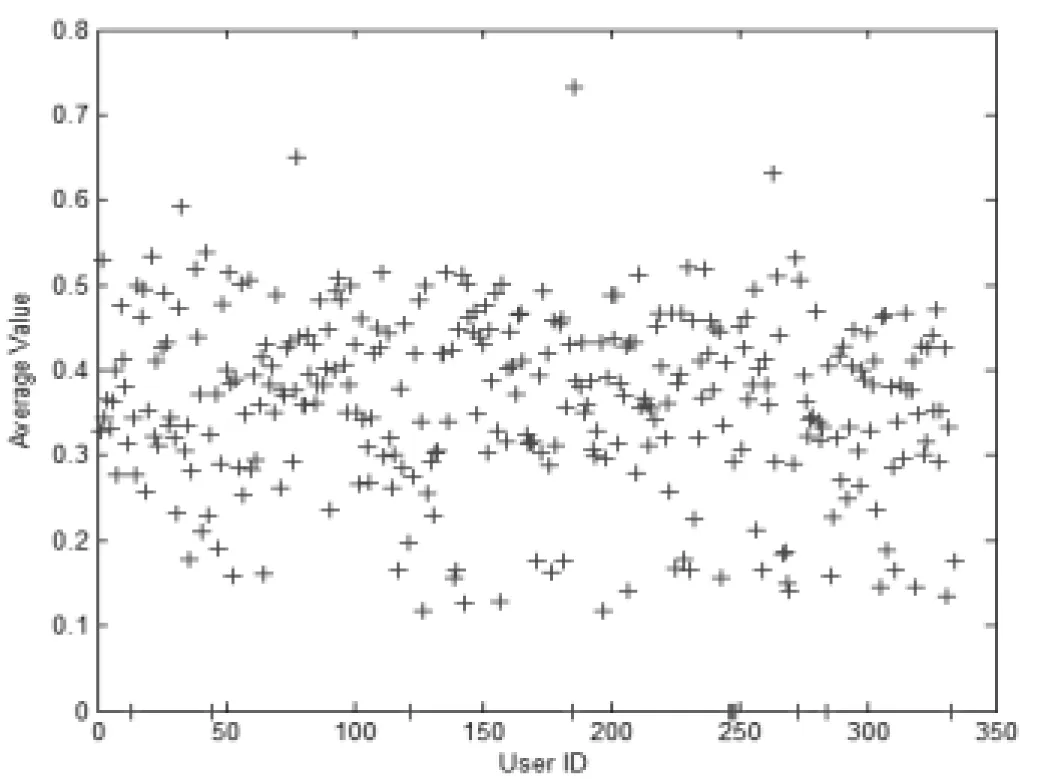
图7 各用户节点的均值

目前，很多节点重要度排序方法并不能有效的将每个节点的重要度清楚的划分，很多特征相似的节点是无法做到精细的排名的。图8给出了所有用户影响力排序(Rank)与其对应均值(AverageValue)之间的关系图。可以看出，除去孤立点外(均值全部为零)，这种重要度划分方法是接近线性关系的，能够将某些相似节点的重要度区分出来。

图8 总排序中各节点的均值

3.3 K-核分解法检验

本文将slavko好友圈的facebook关系网络进行分解，通过比较相同k-壳值节点的排序，来判断排序是否合理。K值的大小需要研究者根据数据自行决定，通常以3、5或10为间隔取k-壳值。为了更细致的说明各个节点的归类情况，现取1为间隔，最终可得到k-壳值分别为0，1，2……，18的分解网络。如图11所示的18-核分解。由于所取间隔较小，存在k-壳值不同的节点的排序交叉集中的现象。

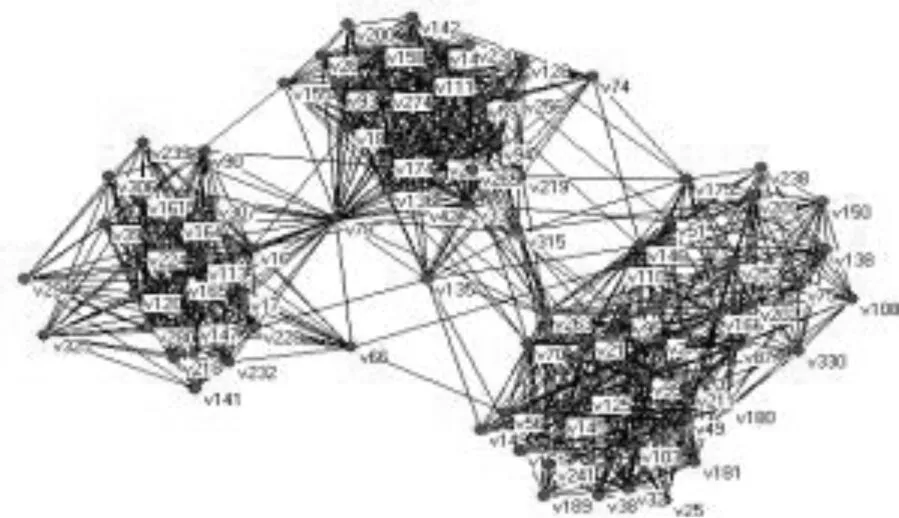
图9 14-核分解

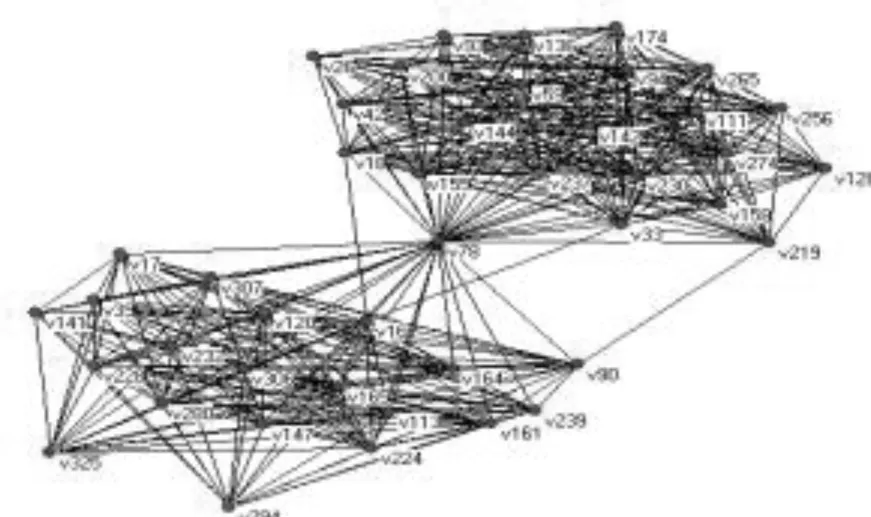
图10 15-核分解

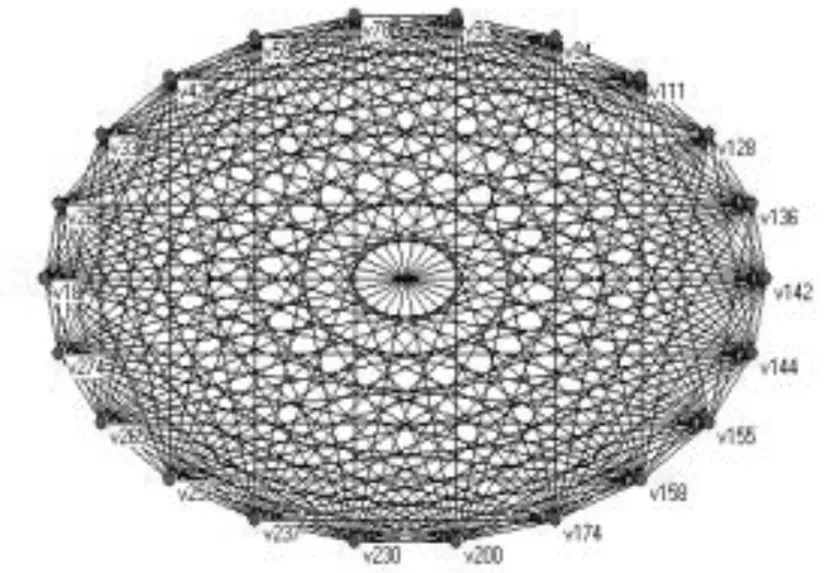
图11 18-核分解

选取部分数据来进行分析。表5给出了间隔分别为1，2，5时的节点排序集中范围的三组数据。选定k壳值间隔，通过比较在此间隔内的节点数目及其对应的排序集中范围和落在此范围内的节点所占比例，可以看出，k-壳值相同的节点的重要性排序是相对集中的，具有相似的影响力，且k-壳值大的节点影响力排名也相对靠前。

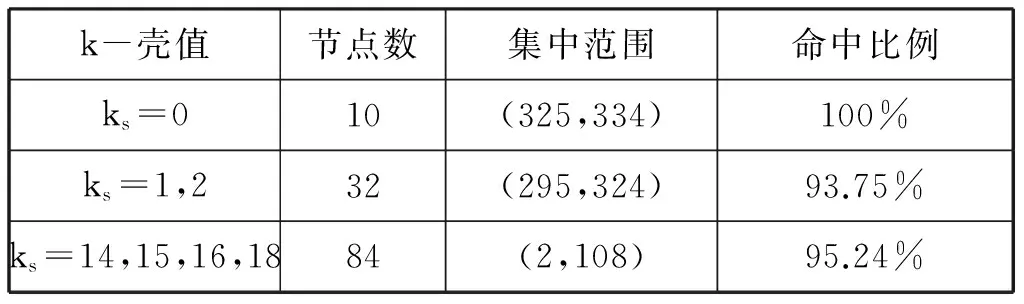
表5 间隔分别为1，2，5的节点排序集中范围

整个网络中各节点的k-壳值与排序分布如图12所示，大部分相同k-壳值节点能够收敛在特定的排序范围内。

图12 各节点的k-壳值与排序分布图

据此，我们可以看出本文所用的社交网络用户影响力评价体系是具有一定科学性的，排序结果也相对准确。

4 与HITS算法的比较与分析

HITS算法是一个经典的网页排序算法，它通过每个节点的权威值与枢纽值相互校正迭代来确定每个节点的影响力值，记为hub值。

建立slavko用户好友圈的有向网络并运用HITS算法计算出各节点的hub值。将本文方法与HITS算法进行结果比较，若取两种方法的影响力排名前30的节点(如表6与表7所示)，则含有17个共同节点，重合率56.67%；若取两种方法的影响力排名前40的节点，则含有32个共同节点，重合率80%；若取两种方法的影响力排名前50名，则含有46个共同节点，重合率92%。可以看出，本文所用排序算法与HITS算法能够在很大程度上吻合。

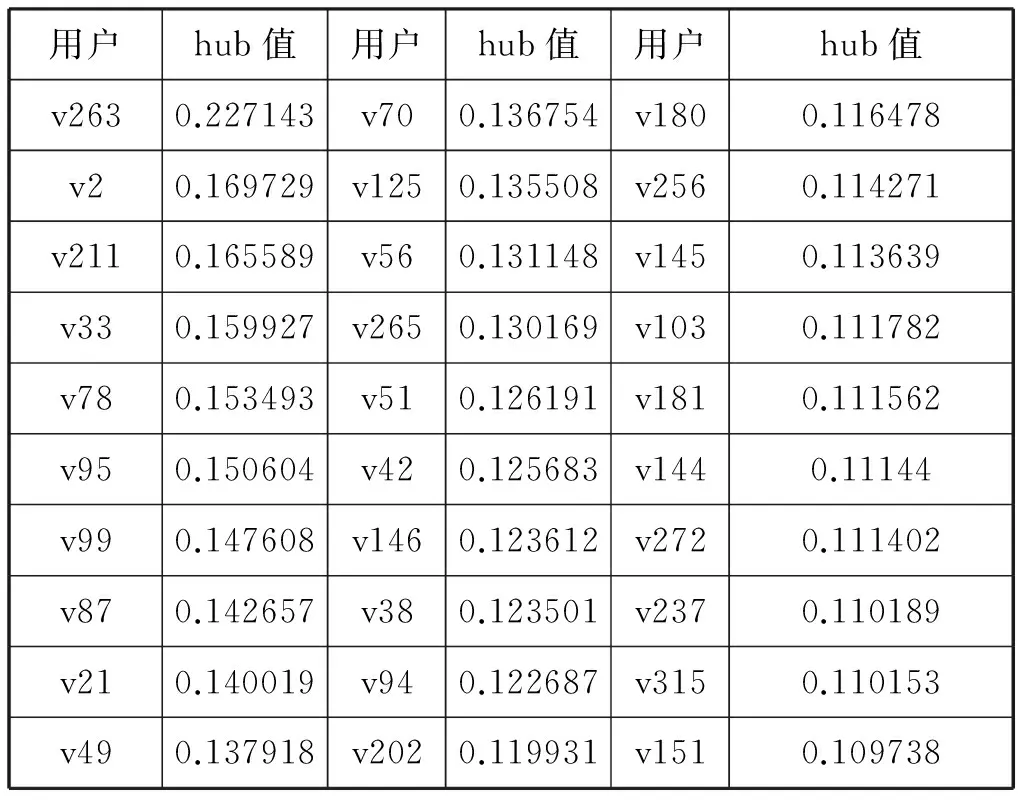
表6 HITS算法排序在1-30名的用户节点的hub值

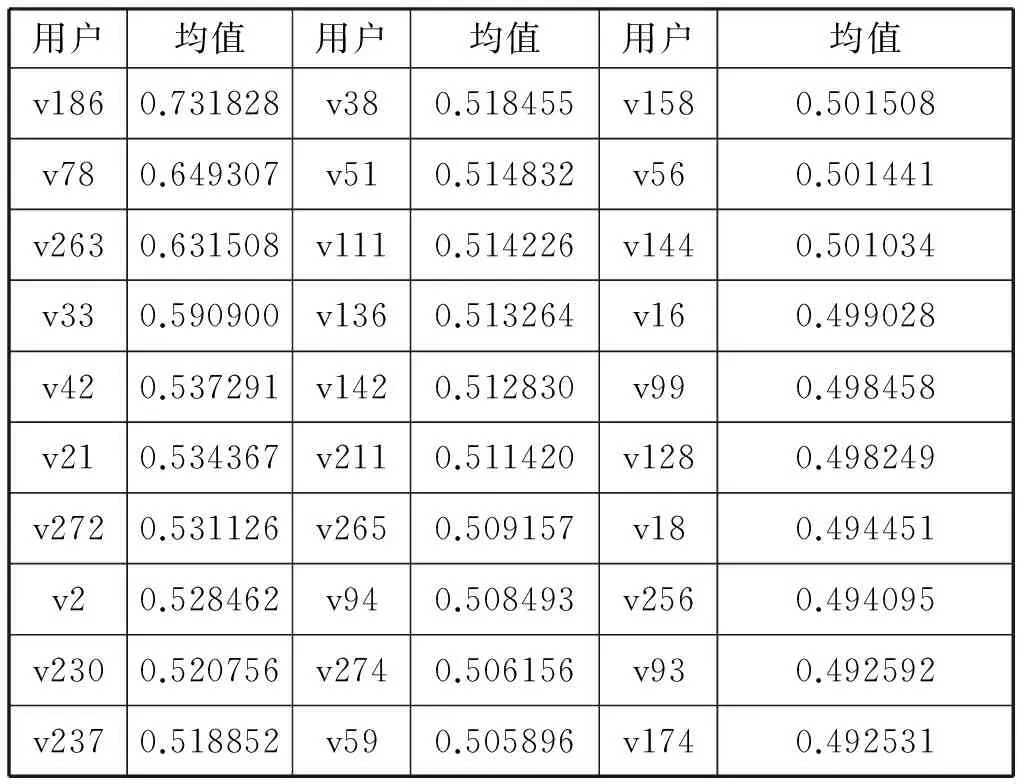
表7 本文所用算法排序在1-30名的用户节点

对于大型的网络，不同的排序算法得到的结果也必然存在差异，这是因为对衡量节点重要度所选取的角度不同，但都具有一定参考意义。通常HITS算法是作用在一定范围的，很容易忽略一些末梢节点，并且易受垃圾连接的影响或发生主题漂移，结果的有效性稍差，而本文方法能够找到HITS算法中一些容易被忽视的重要节点。传统的网页排序算法需要考虑到收敛性和有效性的问题，本文所用方法就无需考虑此问题，对于规模相对小的网络而言，能体现出明显的优势。在适用范围上，网页排序算法通常只适用于特定类型的社交网络，本文方法则可以根据不同规则运用不同类型的社交网络数据建立模型，适用范围更广。

5 总结和展望

本文提出了一种度中心性、介数中心性、接近中心性、聚类系数四指标综合用户影响力评价方法，通过对计算数据归一化处理并取均值得到用户影响力排序。通过仿真实验以及k-核分解、与HITS算法比较验证了此方法的科学性和正确性。这种方法弱化了将有向网络视为无向网络研究而带来的误差，并可以高效地得到重要节点，适用范围更广。

[1]Kleinberg J.Authoritative sources in a hyperlinked environment [J].IBM Research Report，1997，no RJ10076；Journal of the ACM，1999，46(5)：604-632.

[2]Page，Brin S，Motwami R，Winograd T.The PageRank citation ranking：Bring order to the Web [J].Tech Report，Stanford Digital Library Technology Project，1998.

[3]任晓龙，吕琳媛.网络重要节点排序方法综述[J].科学通报，2014，59(13)：1175-1197.

[4]丁兆云，贾焰，周斌，唐府.社交网络影响力研究综述[J].计算机科学，2014，41(1).

[5]Song X，Yun C，Hino K.Identifyirig opinion leaders in the blngosphere[C].the 16th ACM International Conference on Information and Knowledge Management(CIKM’07)，Lisboa，Portugal，2007，971-974.

[6]T H Haveliwala.Topic-sensitive PageRank：a context-sensitive ranking algorithm for Web search[J].IEEE Transactions on Knowledge and Data Engineering，2003，15(4)：784-796.

[7]Zhongwu Zhai，Hua Xu，Peifa Jia.Identifying Opinion Leaders in BBS[J].2008 IEEEWICACM International Conference on Web Intelligence and Intelligent Agent Technology WIIAT 08，2008.

[8]Cha M，Haddadi H，Benevenuto F.Measuring User Influence in Twitter：The Million Follower Fallacy[J].ICWSM，2010，10，10-17.

[9]Ye S，Wu S F.Measuring message propagation and social influence on Twitter.com[M].Berlin ：Springer Berlin Heidelberg，2010，216-231.

[10]Kitsak M，Gallos L K，Havlin S.Indentification of influential spreaders incomplex networks [J].Nature Physics，2010，6(11)：888-893.

[11]Ugander J，Karrer B，Backstrom L.The anatomy of the Facebook social graph[J].2010，aXiv：1111 4503v1.

[12]汪小帆，李翔，陈关荣.网络科学导论[M].北京：高等教育出版社，2012.

(责任编辑：宋金宝)

Research on the Influence of Social Network Users Based on Complex Network

XU Jie1，2，WANG Ju-yun1，ZHANG Hai-yun1

(1.Science School，Communication University of China，Beijing 100024，China；2.School of Information Science and Technology，Beijing University of Chemical Technology，Beijing 100029，China)

Based on complex network theory，analysis of social network users influence can provide support for the study of social marketing，public opinion monitoring，information retrieval，and many other fields.Although it is possible for users to analyze the influence of social networks users based on the traditional PageRank algorithm，but there is still insufficient and high complexity.This article puts forward a kind of evaluation system that evaluate the influence to social network usersbased on undirected network，weakening the error caused by regarding directed network as undirected network，and can quickly get the important nodes，applies more broadly.First of all，using node's degree centrality，betweenness centrality，closeness centrality，clustering coefficient as a network node importance index，calculated by the data normalization and take the mean final evaluation，as a baseline for evaluation of important network node.Secondly，the k-core decomposition method was used to test sorting through coarse-graining to classify the nodes that have similar important degree.Finally，this paper takes an example，and verifies this method of the scientific and correct through the k-core decomposition and comparingwith HITS.

social networks；the influence of users；network node important degree；the k-core decomposition

2016-10-10

徐杰(1993-)，男(汉族)，河北保定人，北京化工大学硕士研究生，E-mail：1207394505@qq.com.

TP

A

1673-4793(2017)02-0067-07