基于改进粒子群算法的横动伺服控制系统辨识*
曹 薇, 罗业才
(1. 广东水利电力职业技术学院 自动化工程系,广东 广州 510925; 2. 华南理工大学 机械与汽车工程学院,广东 广州 510640)
基于改进粒子群算法的横动伺服控制系统辨识*
曹 薇1, 罗业才2
(1. 广东水利电力职业技术学院 自动化工程系,广东 广州 510925; 2. 华南理工大学 机械与汽车工程学院,广东 广州 510640)
针对横动伺服控制系统的黑箱模型,提出了一种基于改进粒子群算法的辨识方法。首先,建立了系统的五阶传递函数模型,其次,在粒子群算法的基础上,引入非线性凹函数作为惯性权重的调整策略,从而避免了算法在寻优过程中陷入局部最优,实现了系统模型的优化。最后,为了验证辨识模型的正确性,进行仿真与实测对比试验。试验结果表明:该算法辨识出的模型准确度较高,具有较好的控制品质,对于同一速度输入信号,仿真与实测的输出曲线跟随性好,误差在-0.5~0.2 rad范围内,误差小。
横动伺服控制系统;粒子群算法;黑箱模型;辨识
0 引 言
横动伺服控制系统是包覆纱机的核心组成部分[1],主要由横动伺服电机、驱动器、嵌入式控制器及PC端组成,通过横动伺服电机驱动钢丝轮正反转带动导纱器来回摆动,实现纱线高速精密卷绕。横动伺服控制系统模型的精确性决定了系统的稳定性和可靠性[2-3],也直接关系到包覆纱机工作效率及工作质量。系统辨识是常用的系统建模方法,通过把系统模型当作未知的黑箱模型,对黑箱模型输入已知信号,测出其输出信号,再利用系统参数估计算法来辨识出系统结构和参数[4-5]。常用的系统参数估计算法可以分为两类:传统算法和智能算法。传统算法主要有最小二乘法[6]等,传统算法是早期的参数估计方法,原理较简单,但不适用于比较复杂的系统。智能算法主要有遗传算法[7]、粒子群算法[8]及神经网络算法[9]等,这些算法一方面很好地弥补了传统算法的不足,另一方面还能够实现全局优化,特别是粒子群算法相对于其他算法来说,由于其粒子搜索趋同性使得其搜索能力更强,收敛速度更快。但是,也容易出现“早熟”,陷入局部最优[10-12]。
为此,本文为了辨识某纺纱机的横动伺服控制系统,提出一种改进粒子群算法来进行系统结构和参数估计,并通过仿真与实测对比试验来验证模型辨识的正确性。
1 横动伺服控制系统数学建模
横动伺服控制系统主要由伺服电机、钢丝轮、钢丝绳、导丝轮、导纱器和卷筒等组成,通过控制伺服电机正反转带动钢丝轮正反转,通过钢丝绳传力带动导纱器来回摆动。横动伺服控制系统模型如图1所示。
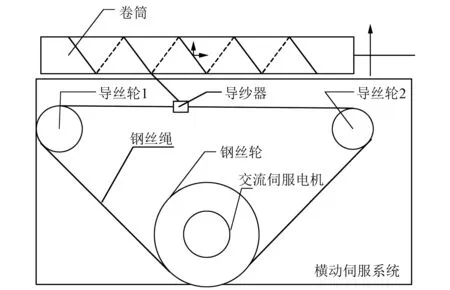
图1 横动伺服控制系统
横动伺服控制系统以PID控制为基础,系统输入为电机角速度,输出为电机角位移,通过三闭环反馈实现高速、高精度控制,如图2所示,从外到内分别为位置环、速度环及电流环。最外环位置环由输入位置信号和反馈位置信号形成闭环控制,位置控制器PD将位置环差分信号作为速度环的输入;中间环速度环由输入速度信号和反馈电机轴转速信号形成闭环控制,速度控制器PI将速度环差分信号作为电流环的输入;最内环电流环由输入电流信号和反馈电机定子电流信号形成闭环控制。

图2 横动伺服控制系统控制系统框图
图2所示系统模型,其传递函数通式为
(1)
式中:a0,a1,a2,b0,b1,b2,b3,b4——横动伺服控制系统待求取参数。
2 改进粒子群算法
横动伺服控制系统辨识就是求取系统传递函数a0,a1,a2,b0,b1,b2,b3,b4这8个未知参数。本文在粒子群算法的基础上,引入非线性凹函数作为惯性权重的调整策略,惯性权值的设置是为了影响粒子的局部搜索能力与全局搜索能力的均衡。主要表示上一代的速度对这一代的速度产生的影响。惯性权值越大,那么表示上一代的速度对当前影响越大,粒子将很大程度的沿着自身上一代的速度移动;如果惯性权值很小,那么表明粒子受上一代的影响很小,粒子将很大程度的沿着自身学习的速度移动。惯性权重大,全局搜索能力增强,局部搜索能力下降;反之,惯性权重降低,全局搜索能力下降,局部搜索能力增强。所以,通过动态调整惯性权重来提高算法性能,一方面提高算法的全局搜索能力,避免陷入局部最优,另一方面减小算法迭代次数,节约辨识时间。
改进粒子群算法表达式如下。
(1) 速度更新公式:
(2)
(2) 位置更新公式:
(3)
(3) 引入非线性凹函数作为惯性权重ω(i)的调整策略:
(4)
式中:k——当前迭代代数;ω——惯性权重;c1、c2——加速因子;r1、r2——0到1的随机数,用来保证群体的多样性;
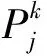
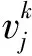


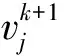
(4) 定义适应度函数。选用误差平方和的倒数作为改进粒子群算法的适应度函数。适应度函数决定了辨识模型与实际模型的相似度,适应度函数值最大时,采样点误差最小,此时辨识参数取得最优值。改进粒子群算法的适应度函数表达
(5)
式中:D——常数(D>0);Ei——第i次采样点的误差;θp(i)——在第i次采样时的实际位移值;θ(i)——第i次采样时利用差分方程求出的结果。
(5) 改进粒子算法运行流程图。改进粒子群算法的运行流程如图3所示。首先,设置最大的速度区间,防止超出最大的区间,位置信息即为整个搜索空间,在速度区间和搜索空间上随机初始化速度和位置,设置群体规模size。对模型参数进行寻优,每个粒子都会记住自己飞行过的最佳位置,同时,所有粒子将各自的最优位置进行共享,建立个体最优位置数据库,那么在这个数据库里必然有一个最最优位置。所有的粒子将按照式(2)和式(3)分别更新位置和速度,所有的粒子将朝着这个最优目标位置飞去。最后,利用适应度函数进行辨识模型和实际模型相似度计算,先检查新粒子适应度是否高于原最优适应度;如果高于则对自己的位置和适应度进行更新,再判断此粒子适应度是否高于全局最优粒子;如果高于则更新全局最优粒子适应度和位置。依此流程进行不断循环迭代,迭代终止条件如下:(1)算法迭代代数达到设定值;(2)相邻两代之间的偏差在一个指定的范围内即停止,达到终止条件,算法结束,输出最优值。
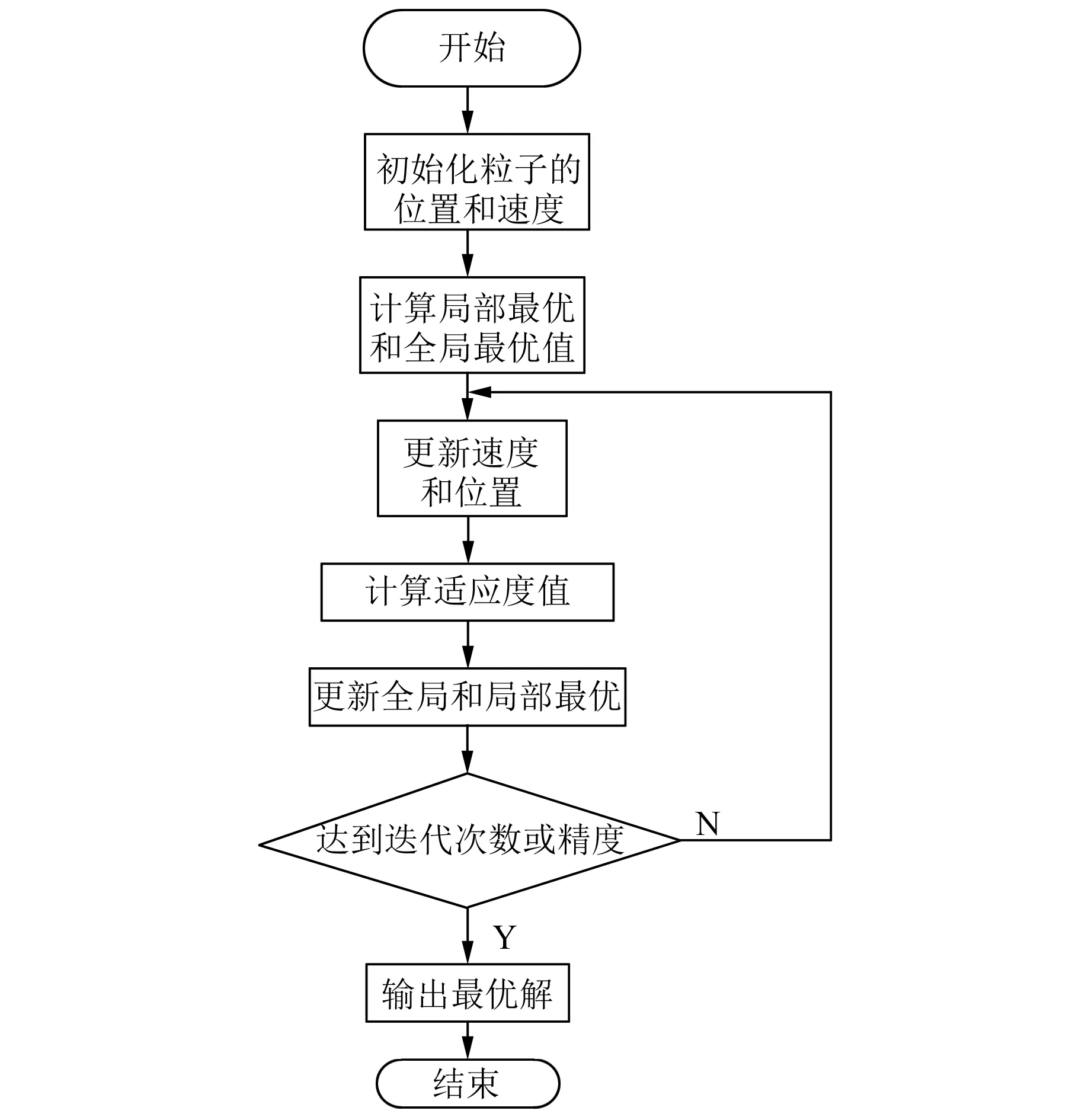
图3 粒子群智能算法流程图
3 系统辨识与试验验证
本文针对如图1所示的横动伺服控制系统,利用改进粒子群算法求取其传递函数式(1)中的a0,a1,a2,b0,b1,b2,b3,b4,设置算法初始参数,设置如表1所示。

表1 改进粒子群算法初始参数设置
粒子群适应度值-进化代数曲线如图4所示。算法在约40代开始收敛,适应度函数取得最大值Fmax=0.074,采样点误差最小。此时,辨识参数取得最优值,如表2所示。

图4 粒子群适应度值-进化代数曲线
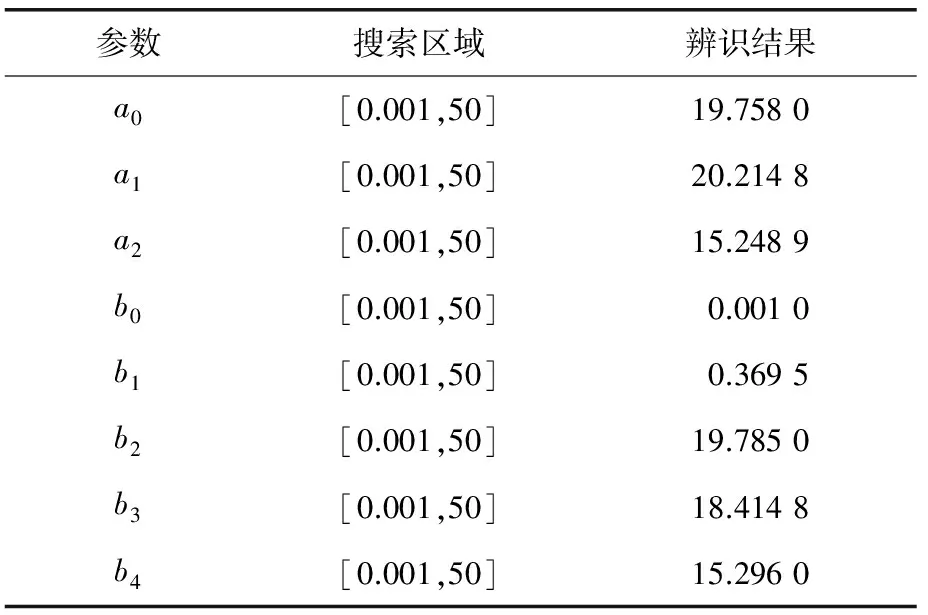
参数搜索区域辨识结果a0[0.001,50]19.7580a1[0.001,50]20.2148a2[0.001,50]15.2489b0[0.001,50]0.0010b1[0.001,50]0.3695b2[0.001,50]19.7850b3[0.001,50]18.4148b4[0.001,50]15.2960
将求取参数代入式(1),得到横动伺服控制系统的模型为
(6)
试验平台如图5所示,主要由横动电机及其驱动器、嵌入式控制器及PC端组成,控制器与伺服电机通过工业以太网EtherCAT总线通信,利用控制器NCTOPLC实时读取系统电机的转角,可以得到其输出曲线及误差曲线。

图5 辨识试验平台
为了验证模型辨识的正确性,输入同一速度信号v(t)=53.25sin(4πt),进行仿真与实测对比试验。试验结果如图6、图7所示。
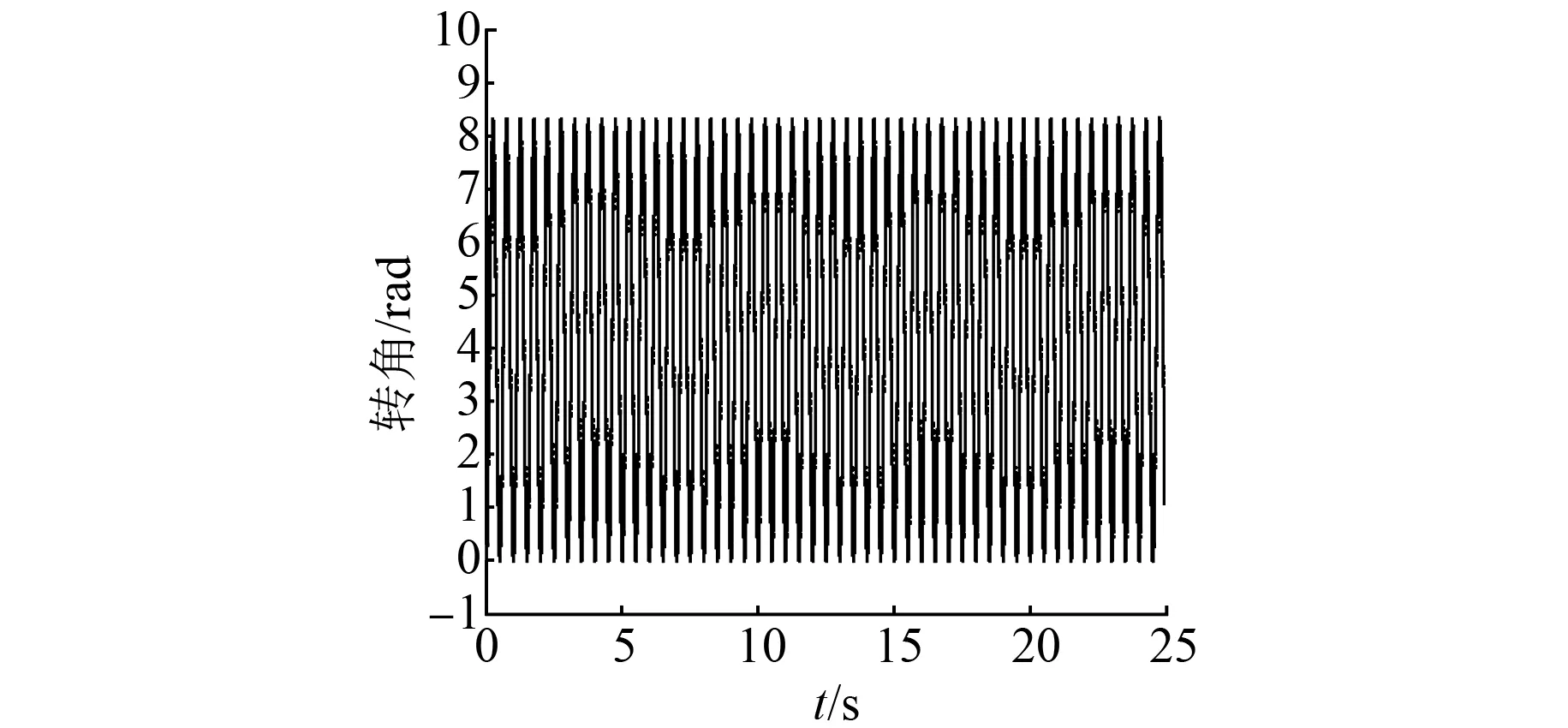
图6 仿真与实测转角输出曲线
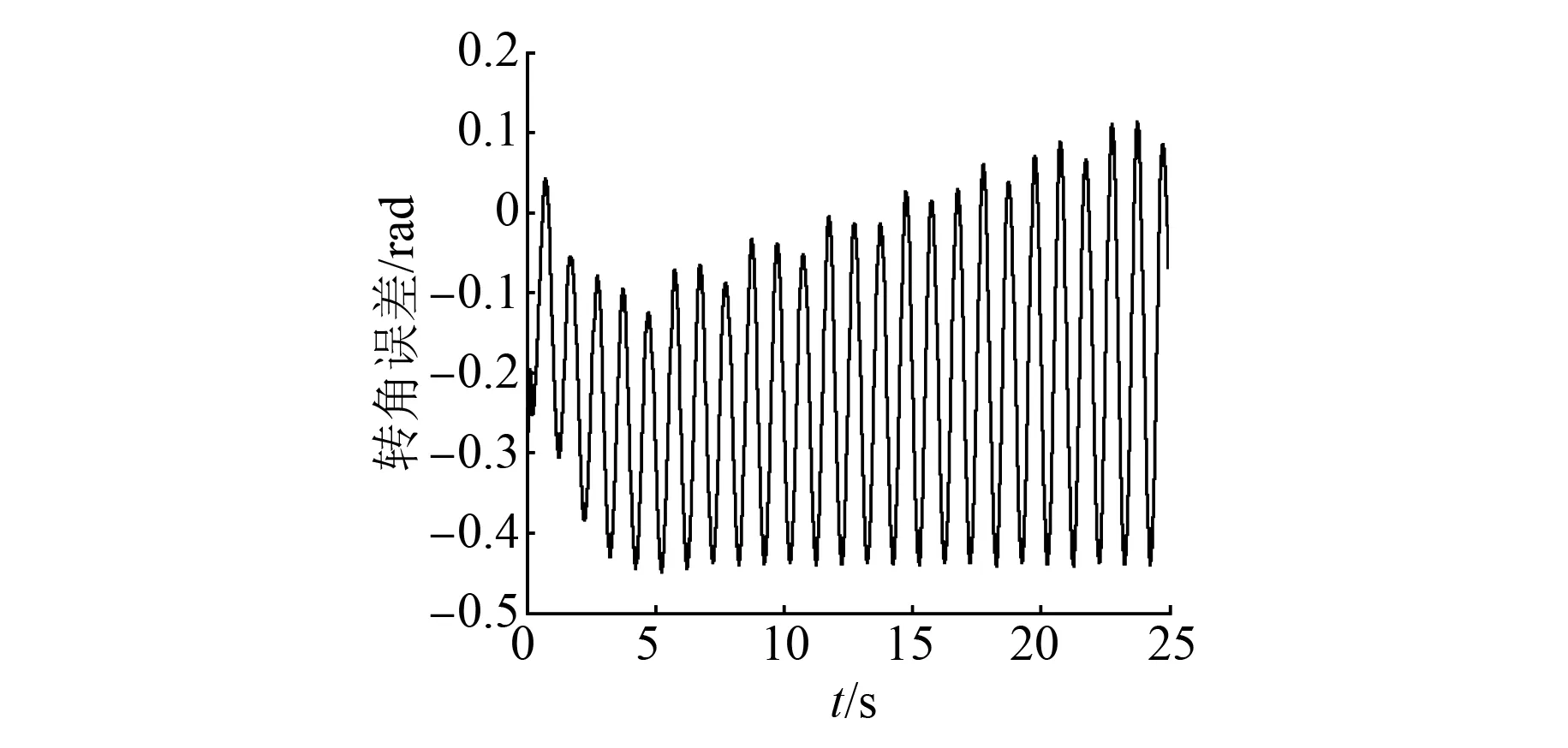
图7 仿真与实测转角输出误差曲线
由图6、图7可知,对于同一输入信号,仿真与实测输出曲线的跟随性好,误差在-0.5~0.2rad范围内,误差小。从而可验证改进粒子群算法辨识出的横动伺服控制系统模型准确度较高,具有较好的控制品质。辨识误差的存在也使系统多了不稳定因素,究其原因,主要是因为实际输入信号中夹杂了干扰信号。
4 结 语
(1) 针对精密卷绕系统中的横动伺服控制系统,建立了其五阶传递函数模型,并设计了一种改进粒子群算法来对该系统的未知参数进行辨识,避免了算法在寻优过程中陷入局部最优,实现了系统模型的优化。
(2) 为了验证辨识模型的正确性,进行仿真与实测对比试验。试验结果表明:该算法辨识出的模型准确度较高,具有较好的控制品质,对于同一速度输入信号,仿真与实测的输出曲线跟随性好,误差在-0.5~0.2rad范围内,误差小。
[1] 马秀凤,张玉清,邢明杰.包覆纺纱技术的现状及发展趋势[J].纺纱导报,2005(10): 141-142.
[2] 王绍斌,孙卫国,王文郁.络筒张力和速度对纱线质量的影响[J].棉纺织技术,2002,30(7): 35-37.
[3] 周云端.专用缠绕机的开发与张力控制系统研究[D].西安: 西北工业大学,2006.
[4] 任贵杰,李平康,赵志刚,等.基于改进遗传算法的单元机组非线性模型参数辨识[J].北京交通大学学报,2011,35(6): 93-97.
[5] 刘胜,宋佳,李高云.PSO并行优化LSSVR非线性黑箱模型辨识[J].智能系统学报,2010,5(1): 51-56.
[6] 李银国,汤卓群,黄镭.非持续激励条件下系统辨识递推最小二乘最小范数算法[J].控制理论与应用,2009,26(4): 365-370.
[7] 肖曦,许青松,王雅婷,等.基于遗传算法的内埋式永磁同步电机参数辨识方法[J].电工技术学报,2014,29(3): 21-26.
[8] 程善美,张益.基于协同粒子群算法的PMSM在线参数辨识[J].电气传动,2012,42(11): 3-6.
[9] 于开平,牟晓明.基于前向神经网络的非线性时变系统辨识的改进递推最小二乘算法[J].振动与冲击,2009,28(6): 107-110.
[10] 刘朝华,章兢,李小花,等.免疫协同微粒群进化算法的永磁同步电机多参数辨识模型方法[J].自动化学报,2012,38(10): 1698-1708.
[11] 靳其兵,张建,权玲,等.基于混合PSO-SQP算法同时实现多变量的结构和参数辨识[J].控制与决策,2011,26(9): 1373-1377.
[12] 赵洋,韦莉,张逸成,等.基于粒子群优化的超级电容器模型结构与参数辨识[J].中国电机工程学报,2012,32(15): 155-161.
Identification of Horizontal Dynamic Servo Control System Based on Improved Particle Swarm Optimization Algorithm*
CAOWei1,LUOYecai2
(1. Department of Automation Engineering, Guangdong Technical College of Water Resource and Electric Engineering, Guangzhou 510925, China; 2. School of Mechanical &Automotive Engineering, South China University of Technology, Guangzhou 510640, China)
In view of the black box model traverse servo control system, an identification method based on improved particle swarm optimization algorithm was proposed. First, the establishment of a system of fifth order transfer function model. Secondly, based on the particle swarm optimization algorithm, the introduction of a nonlinear concave function as a strategy of inertia weight adjustment, so as to avoid the algorithm in search of falling into the local optimum in the process of optimization, the optimization of the system model. Finally, in order to validate the identification model was correct, comparing simulation and actual measurement experiment. The experimental results showed that: the algorithm model was accurate and reliable, with good control quality, for the same speed input signal, simulation and measurement of the output curve tracking was good, the error in the -0.5~0.2 rad range, the error small.
traverse servo control system; particle swarm algorithm; black box model; identification
国家重点研发计划项目(2016YFC0104901);广东水利电力职业技术学院创新强校工程自主创新能力提升类项目(050117);2014年广东省特色创新项目(自然科学类)(2014KTSCX146)
曹 薇(1973—),女,副教授,研究方向为机电一体化。
TM 301.2
A
1673-6540(2017)04- 0043- 04
2016 -09 -20

