双馈直线电机纵向端部效应研究
刘 春, 王 滢, 耿晓芬
(1. 磁浮技术与磁浮列车教育部重点实验室,四川 成都 610031; 2. 西南交通大学 电气工程学院,四川 成都 610031)
双馈直线电机纵向端部效应研究
刘 春1,2, 王 滢1,2, 耿晓芬1,2
(1. 磁浮技术与磁浮列车教育部重点实验室,四川 成都 610031; 2. 西南交通大学 电气工程学院,四川 成都 610031)
建立了双馈直线电机(DFLM)的一维磁场模型,求解了气隙磁通密度表达式。详细分析了气隙磁通密度解析式的构成和各部分对气隙磁场分布的影响,并使用Ansoft Maxwell软件对短初级DFLM进行了建模与仿真。结果表明端部效应在入端随速度的提高而增强,对出端气隙磁场影响很小,可以忽略。由仿真数据可知,相比于直线感应电机,DFLM的纵向端部效应明显减弱。
双馈直线电机;纵向动态端部效应;气隙磁场;一维模型
0 引 言
双馈直线电机(Doubly-Fed Linear Motor,DFLM)初级和次级均填充有交流绕组。DFLM运行时可以只有初级供电,工作于直线感应电机状态;也可以初、次级都供电,工作于双馈状态。且DFLM可以分别调节初级和次级电压的频率、相位、幅值以达到调速目的,故DFLM的调速方式较为灵活。
纵向动态端部效应影响直线电机气隙磁场的分布,进而影响电机的参数和性能,特别是对直线感应电机的运行有着显著的影响。所以对直线电机端部效应的研究对直线电机的运行控制有着重要的意义。关于直线电机端部效应的研究大都基于双边直线感应电机或者永磁直线同步电机,主要采用一维或二维电磁场解析法,以及有限元计算或试验验证等方法。文献[1-2]采用电磁场解析方法求解了气隙磁场的表达式,但是其模型是基于长初级双边结构的直线电机。文献[3]从试验的角度研究了气隙对直线电机运行的影响,但其模型是直线感应电机。DFLM的次级结构与直线感应电机有较大的差别,使得它的端部效应有明显的不同。因此,有必要对直线电机的端部效应模型作适当的调整以适用于DFLM。
本文建立了DFLM的一维电磁场模型,分析了DFLM在考虑纵向动态端部效应时气隙磁通密度的分布。本文还根据样机的参数,利用Ansoft Maxwell 2D软件建立了电机仿真模型,得到了DFLM的气隙磁通密度分布。通过对仿真结果的分析和比较,验证了双馈电机气隙磁场的分布特性和变化规律。
1 DFLM一维磁场模型
以短初级DFLM作为分析对象,其结构如图1所示。电机的初级和次级均布有三相交流绕组,初级和次级绕组的供电可进行单独调节。

图1 DFLM纵向剖视图
分析时,用电流层代替绕组,电流层随时间作正弦规律变化,忽略铁心饱和影响。气隙长度相比于电机宽度小得多,忽略气隙磁场沿垂直方向的变化,即气隙磁场只与纵向长度有关[4]。由此,可以建立DFLM的一维模型,如图2所示。
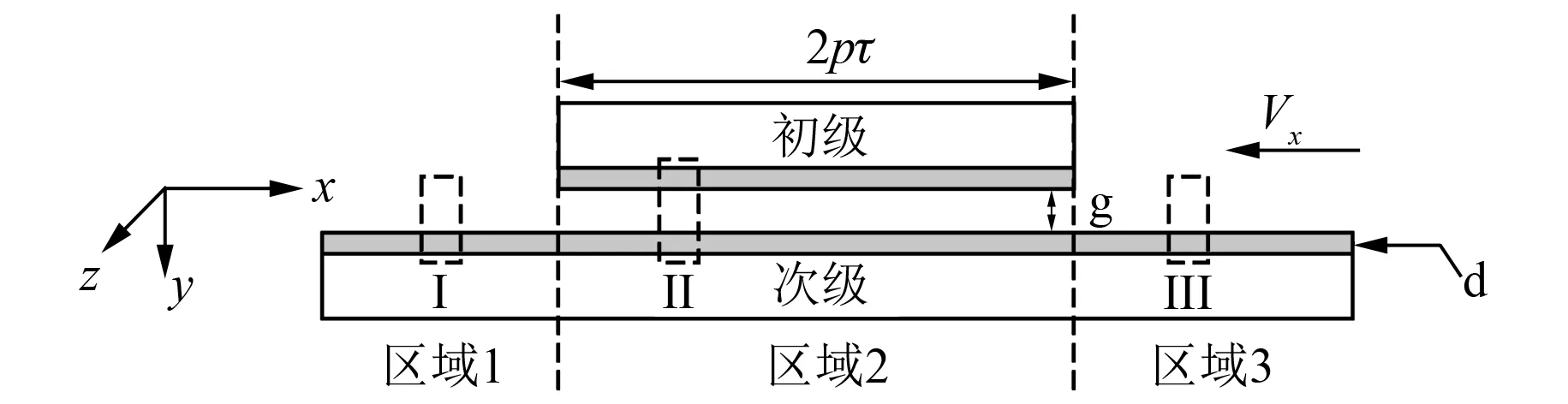
图2 DFLM一维模型
如图2所示,参考坐标系固定在初级的左端边缘处,x轴沿电机纵向,位于初级的中心线上。电流层只沿z轴流动,y轴由初级指向次级。忽略横向端部效应和气隙磁场沿y轴的变化。这样可把气隙磁场简化为一维磁场。初级长度为2pτ,τ为电机初级极距,p为极对数。设初级行波电流层为
(1)
次级行波电流层为
(2)
其中:k=π/τ
式中:ω1、ω2——初级和次级的供电频率;J1m、J2m——电流幅值。
在区域2中,初级运动时可得次级感应电动势:
(3)
又有
(4)
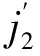
νx——初级沿x轴移动的速度。
对于形环回路Ⅱ,由全电流定律可得
(5)
式中:g′——电机的电磁计算气隙,g′=Kcg;Kc——卡氏系数。
正常运行时,初级和次级的磁场相对静止,以初级作参考则两者的频率同为同步角频率。设同步角频率为ω,由式(5)可得
(6)
式(6)是一个二次非齐次线性方程,将式(1)、式(2)代入可求出磁通密度表达式如下:
(7)


B1、B2——根据边界条件确定的常数。
环形回路Ⅰ和Ⅲ中只存在次级电流层,气隙中心线到次级表面的距离远小于次级宽度。感应电流在区域1和3中迅速衰减,且其值与次级电流相比很小,所以y=0的中心线上的磁场可以只考虑次级电流j2产生的磁场,有如下关系式:
(8)
(9)
根据行波电流层的解析式可得
(10)
(11)
在x=0和x=2pτ处,由分界面上磁场强度切向分量相等的磁场分界条件可得
(12)
由此可以求出系数B1和B2:
(13)
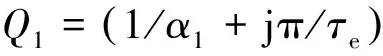
将式(13)代入式(7)即可求得气隙磁通密度表达式。
根据表达气隙磁场的式(7)可知,与直线感应电机类似,DFLM的气隙磁场也是由三种行波磁场构成的。右端第一项不衰减的波长为2τ的前进行波磁场;第二项入端行波磁场,沿x轴正向移动,衰减系数为1/α1,波长2τe;第三项出端行波磁场,沿x轴负向移动,衰减系数为1/α2,波长2τe。入端和出端行波磁场都是由初级铁心断开所引起的,他们常被称为“终端效应波”[5]。由衰减系数的表达式可知,速度越高,入端行波衰减系数1/α1越小,说明入端行波衰减速度减小,其透入长度变长,而出端行波变化相反。电机在高速运行时入端行波磁场甚至超过整个初级铁心的长度,对整个气隙磁场都将产生影响。此时的出端行波磁场气隙迅速衰减,其影响可以忽略。
2 仿真与分析
采用Maxwell2D建立DFLM模型,如图3和图4所示。电机主要参数如表1所示。

图3 DFLM仿真模型
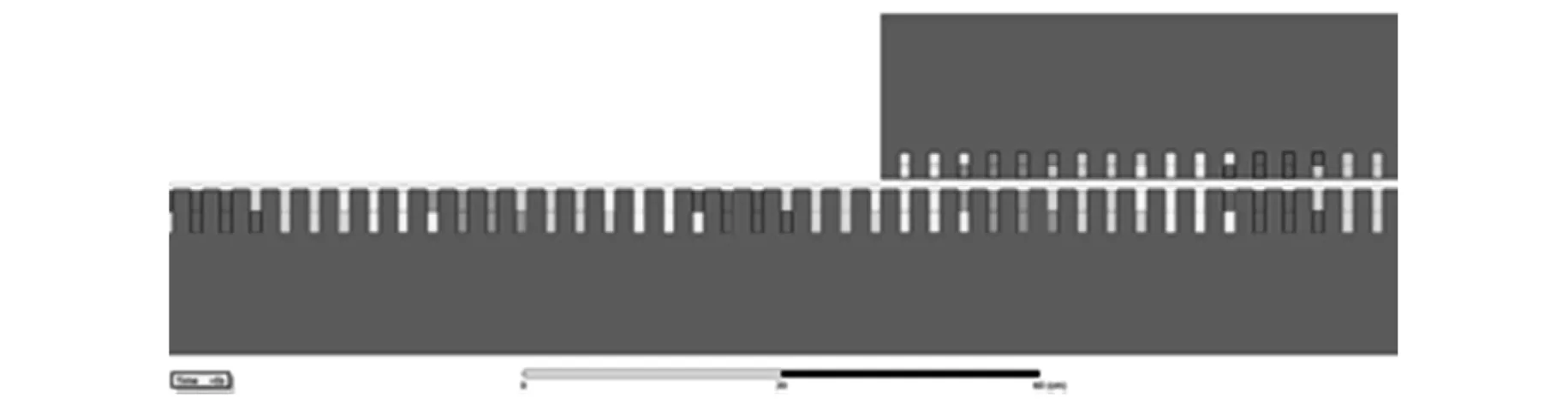
图4 DFLM仿真模型局部
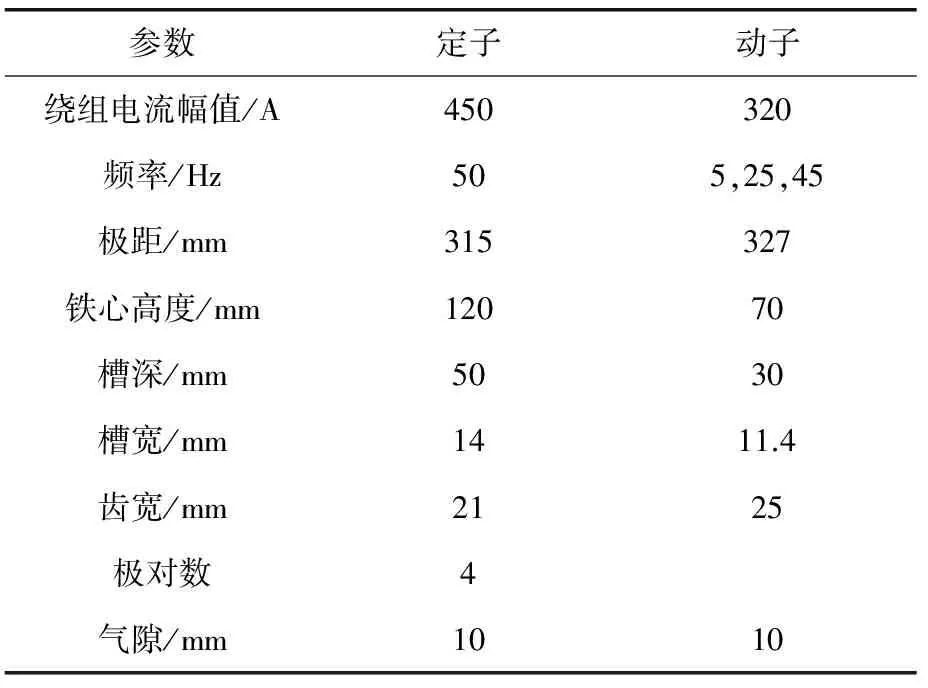
参数定子动子绕组电流幅值/A450320频率/Hz505,25,45极距/mm315327铁心高度/mm12070槽深/mm5030槽宽/mm1411.4齿宽/mm2125极对数4气隙/mm1010
仿真中,给定激励为对称的随时间作正弦变化的电流。定子供电频率50 Hz,动子的供电频率根据动子运行速度给定以保证稳定的推力。例如定子供电频率50 Hz,决定了电机的同步速度是31.5 m/s,当电机运行速度为22.05 m/s时,动子供电频率应该为15 Hz。模型主要研究直线电机在低速时的纵向端部效应,取3组不同速度下电机稳定运行时的气隙磁场数据,作出气隙磁通密度沿横向坐标分布图,同时给出理论计算曲线。
如图5所示,横坐标为动子长度两端各延伸两个极距的距离,并作归一化处理。纵坐标为气隙磁通密度幅值,矩形虚线框表示动子所在位置,动子长度为2.52 m,左边为入端,右边为出端。图5(a)、图5(c)、图5(e)曲线为仿真数据波形,图5(b)、图5(d)、图5(f)曲线为计算值波形。由图5(a)~图5(f)可以看出,随着速度的提高,入端的气隙磁场幅值逐渐减小,幅值减小的范围也逐渐扩大。速度为3.15 m/s时,入端磁通密度幅值削弱的范围在一个τ左右,速度升高到28.35 m/s时,削弱范围扩大到2τ左右,此时相比于中部峰值削弱了约15%。中部气隙磁场减弱到约0.8 T,相比于低速时的0.9 T减弱了约12.5%。靠近出端的部分,速度的增加使得出端磁场有所增加,增加幅度约为10%。

图5 不同速度下气隙磁通密度分布情况
根据气隙磁场波形可知,计算值和仿真数据能够较好地吻合。由于仿真中存在明显的齿槽影响,所以造成气隙磁场出现较多的尖峰端,加之实际中电机参数的时变性使得精确的衡量端部效应十分困难,所以此处主要参考数据的变化趋势。由此可知,DFLM的纵向端部效应削弱了入端处的气隙磁场,对出端气隙磁场影响很小;随着速度的提高,对入端的削弱作用逐渐增强,而对出端的影响几乎不变。
图6是直线感应电机在保证平均推力和DFLM相同、动子速度28.35 m/s时的气隙磁通密度波形。从图6可知,气隙磁密幅值约0.8 T,入端的气隙磁密约为0.3 T,削弱范围从入端延伸了3~4τ,较中部峰值削弱了约63%。由此可知,相同推力条件下,DFLM入端气隙磁场的削弱程度约为直线感应电机的1/4,入端行波的延伸距离约为直线感应电机的1/2,纵向端部效应明显弱于直线感应电机。
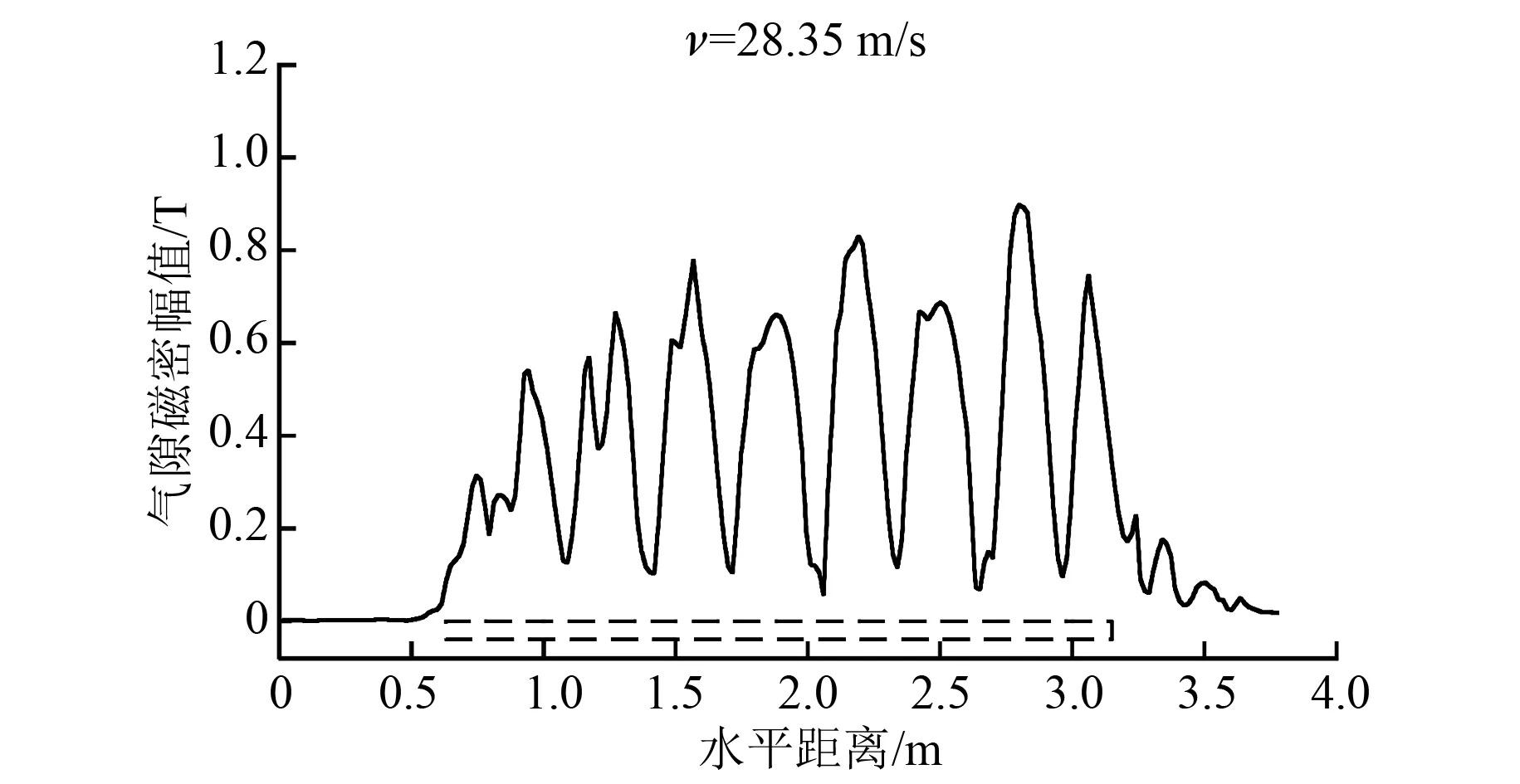
图6 电机感应气隙磁通密度分布
3 端部效应特性分析
DFLM和直线感应电机的纵向端部效应有相似的变化规律,但也有自己的特点。气隙解析式中α1和α2也称作透入长度,衡量端部效应波从边端透入气隙的距离[6],表达式如下:
(14)
由式(14)可知,透入长度λ与次级电导率s和电机运行速度ν有关。当电机结构确定时,透入长度主要与电机的运行速度有关。
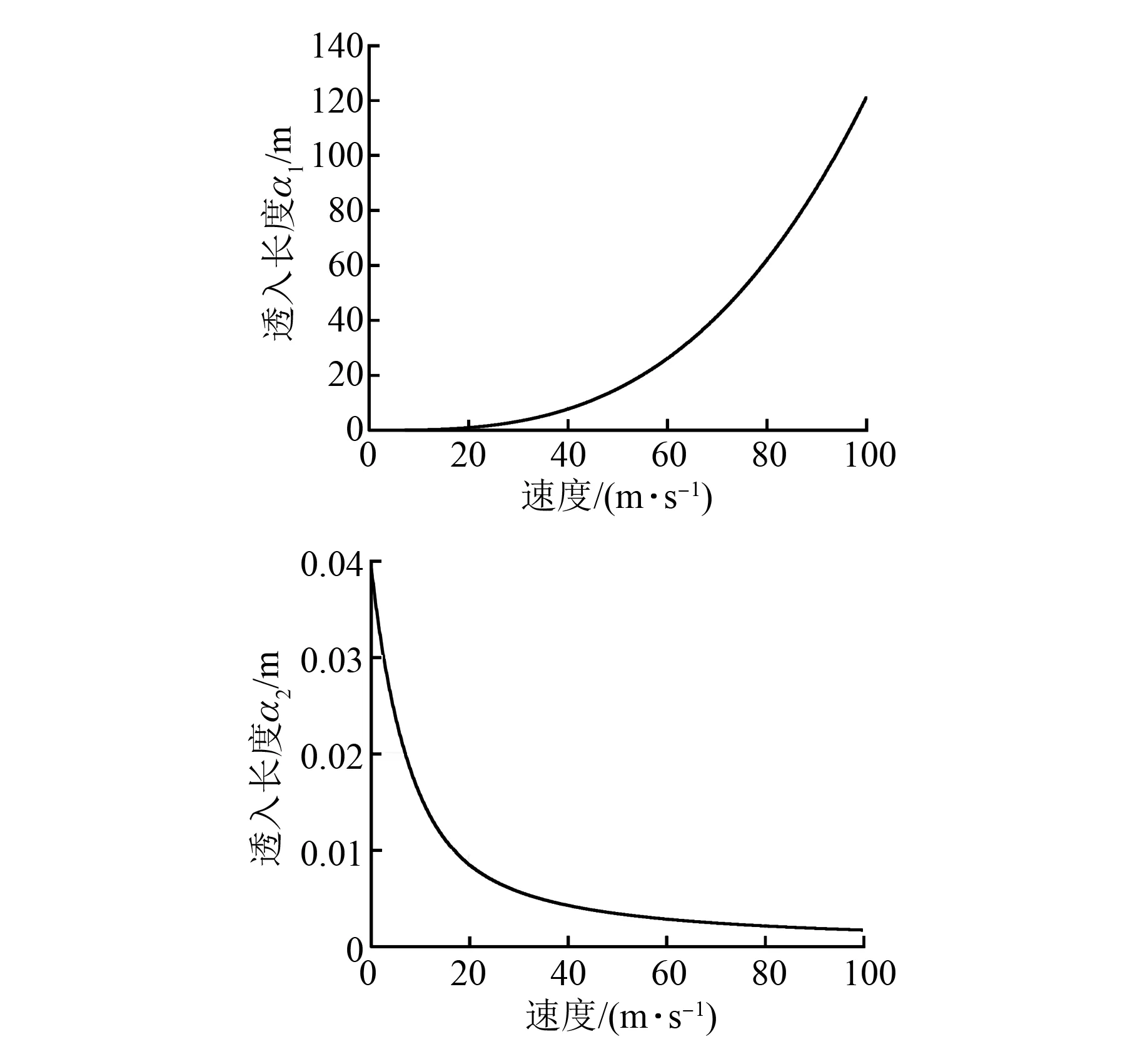
图7 速度ν与透入长度λ的关系
图7是由式(14)计算而得的透入长度λ与电机速度ν的关系图,次级材料为铝。结合图5气隙磁通密度波形可知,随着速度的升高,入端行波磁场透入长度迅速增加,距离入端较远的气隙磁场也出现了削弱。出端行波磁场的透入长度迅速减小,它对出端的磁场影响很小。
表2是速度为28.35 m/s时不同材料次级对应的透入长度理论计算值。由表2可以看出,次级材料的电导率越高,入端透入长度越长,出端透入长度越小且迅速减小至可以忽略。

表2 次级材料与透入深度的关系
本次仿真中采用WD65_50硅钢的次级,分布有三相交流绕组。从结构上看,次级槽中的绕组通有三相交流电,次级供电电流远大于感应电流,所以其感应电流作用很小。在电机设计时,可以考虑选取适合的次级材料和次级供电方式抑制纵向端部效应。
4 结 语
本文采用一维磁场模型推导了DFLM考虑边端效应时气隙磁场的表达式。由计算与仿真数据表明,DFLM运行时入端气隙磁场被削弱,出端气隙磁场变化很小,相比于直线感应电机,其端部效应大幅减弱。DFLM的次级绕组结构能够有效地削弱纵向动态端部效应,在对其调速控制时,可在较大的速度范围内忽略纵向端部效应,为控制提供便利。气隙磁场的计算和仿真结论可为该种电机的运行控制提供参考。
[1] 杨通,周理兵.长初级双边直线感应电机纵向动态端部效应第一部分:气隙磁场[J].电机与控制学报,2014,18(4): 52-59.
[2] 鲁军勇,马伟明,李朗如.高速长初级直线感应电动机纵向边端效应研究[J].中国电机工程学报,2008,28(30): 73-78.
[3] 李志宏,强雄,计丽霞,等.直线感应电动机磁场气隙的分析及试验设计[J]. 电机与控制应用,2015,42(8): 86-88.
[4] 龙遐令.直线感应电动机的理论和电磁设计方法[M].北京:科学出版社,2006.
[5] YAMAMURA S. Theory of Linear Induction Motors[M]. Wiley Interscience, 1972.
[6] 卢琴芬.直线同步电机的特性研究[D].杭州: 浙江大学, 2005.
Study on Longitudinal Dynamic End-Effect of Doubly-Fed Linear Motor
LIUChun1,2,WANGYin1,2,GENXiaofen1,2
(1. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle Ministry of Education, Chengdu 610031, China; 2. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China)
The one-dimensional field model of a doubly-fed linear motor was established (DFLM), and the air gap magnetic field expressions was given. The gap magnetic flux density composition and its effect of all parts on the air-gap magnetic field distribution were analyzed, and model and do simulation a short primary DFLM running at low speed with Ansoft Maxwell. The results showed that end-effect enhanced at the in-side and too weaken to be ignored at the out-side. According to the simulation, compared to the LIM, DFLM′s end-effect was significantly reduced.
doubly-fed linear motor (DFLM); longitudinal dynamic end-effect; air-gap field; one dimensional model
刘 春(1991—),男,硕士研究生,研究方向为直线电机驱动技术。 王 滢(1972—),女,副教授,研究方向为磁悬浮技术。 耿晓芬(1992—),女,硕士研究生,研究方向为磁悬浮技术。
TM 359.4
A
1673-6540(2017)04- 0034- 05
2016 -07 -11

