三角载波层叠PWM算法的数字实现与优化*
杨成子, 黄 萍
(上海大学 机电工程与自动化学院,上海 200072)
三角载波层叠PWM算法的数字实现与优化*
杨成子, 黄 萍
(上海大学 机电工程与自动化学院,上海 200072)
研究了级联型多电平逆变器的三角载波层叠PWM控制的数字实现方法,并对其固有的开关管发热不均的问题进行了优化。最后在两单元级联型多电平逆变器试验平台上验证了数字实现方法及其优化方法的有效性和可实现性。
级联型多电平逆变器;三角载波层叠;PWM控制
0 引 言
多电平技术主要用于中高压脉宽调制(Pulse Width Modulation,PWM)电压源型逆变器。为了减小输出电压的谐波含量,多电平逆变器控制策略主要有正弦脉宽控制[1-3]和空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)控制[4-6]。
其中正弦脉宽控制,是由以冲量等效原理为基础的两电平正弦脉宽调制(Sinusoidal Pulse Width Modulation,SPWM)技术发展而来的。主要有:三角载波移相PWM控制、三角载波层叠PWM控制、分段层叠PWM控制等。三角载波移相PWM控制是将不同功率单元三角载波相移2π/N(N为每相级联H桥个数),使得两个功率单元输出电压脉冲之间有相位差别,通过叠加N个单元的输出电压可以得到2N+1电平输出电压;三角载波层叠PWM控制使用N个幅值和频率相同的三角波(相位关系有不同安排)在纵轴方向上下连续排列作为载波,与同一调制波进行比较,得到不同时刻的输出电平,叠加成为多电平输出;分段层叠PWM控制则适用于混合级联型逆变器的输出电压。
本文对应用在级联型多电平逆变器中的三角载波层叠PWM控制进行深入研究,探讨其数字实现方法与优化方法。
1 级联多电平逆变器的三角载波层叠PWM算法
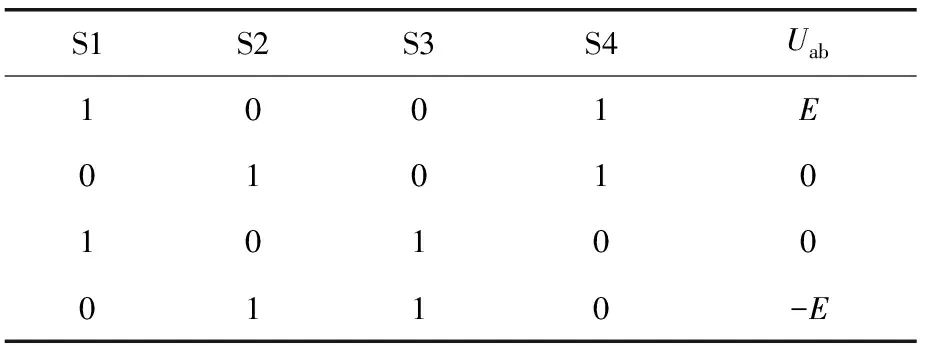
级联型多电平逆变器拓扑结构如图1所示。每相由n个功率单元串联组成。图2所示为H桥式功率单元的主电路拓扑结构,该功率单元可以输出-E、0、E三种电平,开关管S1和S3、S2和S4互为互补开关管,互补开关管不同时导通。各开关管开通状态与功率单元输出电压对应关系如表1所示。

图1 级联型多电平逆变器三相基本结构

图2 级联型多电平逆变器H桥式功率单元
S1S2S3S4Uab1001E01010101000110-E
理论分析表明,n个功率单元输出电压相互叠加,可以输出2n+1电平的相电压,输出4n+1电平的线电压,从而实现使用低耐压开关器件输出高等级电压的目的。
三角载波层叠PWM,既适用于二极管/电容钳位型逆变器,也适用于具有独立直流源的级联型逆变器。当采用N个幅值和频率相同的三角波在纵轴方向上下连续排列作为载波,与同一调制波进行交截比较后得到不同时刻的输出电平,随之确定各个开关管的开通关断状态,最后最多可以输出2N+1个电平。根据三角载波在纵轴方向排列时相位的关系,三角载波层叠PWM控制可以分为以下三种:(1)同相层叠法(Phase Disposition,PD),即三角载波在纵轴方向上相位相同,如图3(a)所示;(2)交替反相层叠法(Alternative Phase Opposition Disposition,APOD),即相邻的三角载波在纵轴方向排列时相位相反,如图3(b)所示;(3)正负反相层叠法(Phase Opposition Disposition,POD),即横轴以上的三角载波同相位,横轴以下的三角载波同相位并与横轴以上的三角载波反相,如图3(c)所示。
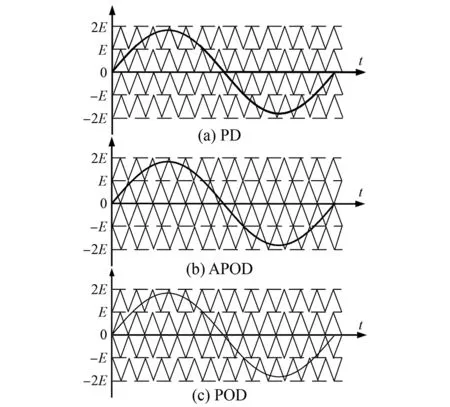
图3 载波层叠PWM
以两单元级联的级联型逆变器为控制对象和同相层叠PWM为控制方法为例,驱动信号产生形成过程如图4所示[7]。正弦波发生器根据幅值给定和频率给定产生相应幅值和频率的正弦波给定Ur,三角波发生器产生N个纵轴方向上层叠的三角载波Uc1、Uc2、Uc3、Uc4,分别与正弦波比较。H桥1的驱动信号由Ur和Uc1、Uc2比较产生。当Ur>Uc1时,使S1开通,S4关断;当Ur 图4 三角载波层叠PWM驱动电路 三种载波层叠PWM实现的基本方法一致,但通过数学分析可知,PD消谐波性能最优,尤其是消除线电压波形中的谐波;APOD输出电压相比POD拥有更多的3次边带谐波成分,所以其消除线电压谐波作用强于POD。 随着数字处理器的迅速发展,数字控制系统相对于模拟系统具有硬件简单、通用性好、抗干扰能力强、算法灵活等优点,数字控制技术已经成为主流。 PWM波形的数字控制有自然采样法、规则采样法。自然采样法虽然控制精度高,但正弦波和三角波交点时刻不便于通过数字计算获得。规则采样法分成对称规则采样法和不对称规则采样法。对称规则采样法是从自然采样法演变而来的,经过采样的正弦波(实际上是阶梯波)与三角波相交,由交点得出脉冲宽度。这种方法只在三角波的顶点或底点位置对正弦波采样而形成阶梯波。对称规则采样法原理图如图5(a)所示。不对称规则采样法采用在每个载波周期采样两次,即在三角波的顶点位置采样,又在三角波的底点位置采样,形成的阶梯波与正弦波的逼近程度会大大提高。不对称规则采样法生成SPWM的原理图如图5(b)所示。由图5(b),根据三角形相似定理可得 (1) (2) 式中:Tc——三角载波的周期;tA、tB——一个周期内的两个采样点;a——调制度,0≤a<1;ω——正弦调制波角频率;tD——在三角波的负峰对正弦信号波的采样时刻; δ——A相开通时刻脉冲宽度。 由式(1)、式(2)可得 (3) 图5 SPWM波形的采样 三角载波层叠PWM控制的数字实现的基本思路为将坐标轴位置调整至适合利用规则采样法计算的位置,如图6所示。图6(a)为变换后的最上层的三角载波与正弦调制波,将坐标轴上移E刻度后得到新的坐标系,将新的坐标系中的正弦波表达式代入式(3)中,计算得到左桥臂S1占空比,将其取反得到S2占空比。同样地,如图6(b)所示,将新的坐标系中的正弦波表达式代入式(3)中,计算得到右桥臂S3占空比,将其取反得到S4占空比。 图6 开关占空比计算 为了验证上述三角载波层叠PWM法数字实现方法的可行性,搭建了由两个如图2所示的功率单元级联而成的单相级联型多电平逆变器,E取50 V。开关管开关频率取7.2 kHz。选用微芯(Microchip)公司的16位单片机dsPIC33EP512M U810作为数字控制器,利用其高速PWM模块生产各个开关管的驱动信号。 驱动信号如图7所示。图7(a)为H桥1驱动信号,图7(b)为H桥2驱动信号,由上而下分别为开关管S1、S2、S3、S4的驱动信号。 图7 驱动信号 图8为输出电压波形。其中,曲线a为H桥1输出电压波形,曲线b为H桥2输出波形,曲线c为级联输出电压波形。 图8 输出电压波形 由图8曲线a和曲线b可以看出,H桥1和H桥2开关管开关次数不同。以前述试验为例,H桥1每周期内开关次数为39次,H桥2每周期内开关次数为25次。长期在这种不均衡的状态下运行,会导致两个功率单元开关管发热量不均匀,影响系统寿命和可靠性。图9为普通的三角载波层叠控制下,直流母线电压取50 V,负载为100 Ω电阻性负载,工作10 min时开关管温度图。从图9可明显看出,H桥1开关管S3温度为39.7 ℃,H桥2开关管S3温度为37.8 ℃ ,相差1.9 ℃,不同功率单元之间发热不均匀现象严重。 图9 普通的三角载波层叠控制下开关管温度图 为了克服该缺点,优化三角载波层叠PWM控制,每M个周期将H桥1与H桥2驱动信号对调,长期运行下各个开关管开关次数相同。优化后的H桥1开关管驱动信号及其输出电压波形,如图10所示。长期运行下,H桥1和H桥2各个开关管开关次数基本相同。 图10 优化的三角载波层叠控制下H桥1 图11为优化三角载波层叠控制下,直流母线电压取50 V,负载为100 Ω电阻性负载,工作10 min时开关管温度图。由图11可以看出,H桥1开关管S3温度为38.8 ℃,H桥2开关管S3温度为38.9 ℃,不同功率单元之间发热不均匀现象被抑制。 图11 优化的三角载波层叠控制下开关管温度图 本文给出了级联型多电平逆变器三角载波层 叠PWM算法的数字实现方法以及针对其不同H桥开关管发热不均匀问题的优化方案,并在单相两单元级联型多电平逆变器试验平台上验证了数字实现方法及其优化方法的有效性和可实现性。 [1] 徐凤君.多电平逆变器技术及其应用[M].北京: 机械工业出版社,2007. [2] MALINOWSKI M, GOPAKUMAR K, RODRIGUEZ J, et al. A survey on cascaded multilevel inverters[J]. Industrial Electronics, IEEE Transactions on, 2010, 57(7): 2197-2206. [3] 王琨,冯琳,李国杰.一种适用于飞跨电容型多电平逆变器的新型载波同相层叠PWM方法[J].电力系统保护与控制,2014,42(14): 8-13. [4] 吴凤江,孙力,赵克.级联型逆变器的新型简化多电平空间矢量调制方法[J].中国电机工程学报,2009,29(12): 36-40. [5] 赵辉,胡仁杰.SVPWM的基本原理与应用仿真[J].电工技术学报,2015,30(14): 350-353. [6] NUPUR M, BINDESHWAR S, SINGH S P, et al. Multilevel inverters: a literature survey on topologies and control strategies[C]∥ International Conference on Power, Control and Embedded Systems, Perth, Australia, 2012: 1-11. [7] 陈坚,康勇.电力电子学[M].北京: 高等教育出版社,2011. Digital Implementation and Optimization of Multicarrier Level-Shifted PWM Algorithm* YANGChengzi,HUANGPing (School of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China) The digital implementation method of multicarrier level-shifted PWM algorithm for cascaded multilevel inverters was studied. And the inherent problem of uneven heating of switch was optimized. Finally, the digital implementation and its optimization method were verified on the experimental platform of the two cell cascaded multilevel inverter. cascade multilevel inverter; multicarrier level-shifted; PWM control 国家高技术研究发展(863)计划(2011AA11A247);上海市科委重点项目(14DZ1206300);上海市经信委重大技术装备项目(ZB-ZBYZ-02-14-0825) 杨成子(1993—),男,硕士研究生,研究方向为中、大功率变频器。 黄 萍(1993—),女,硕士研究生,研究方向为电力电子与电力传动。 TM 301.2 A 1673-6540(2017)04- 0047- 05 2016 -10 -24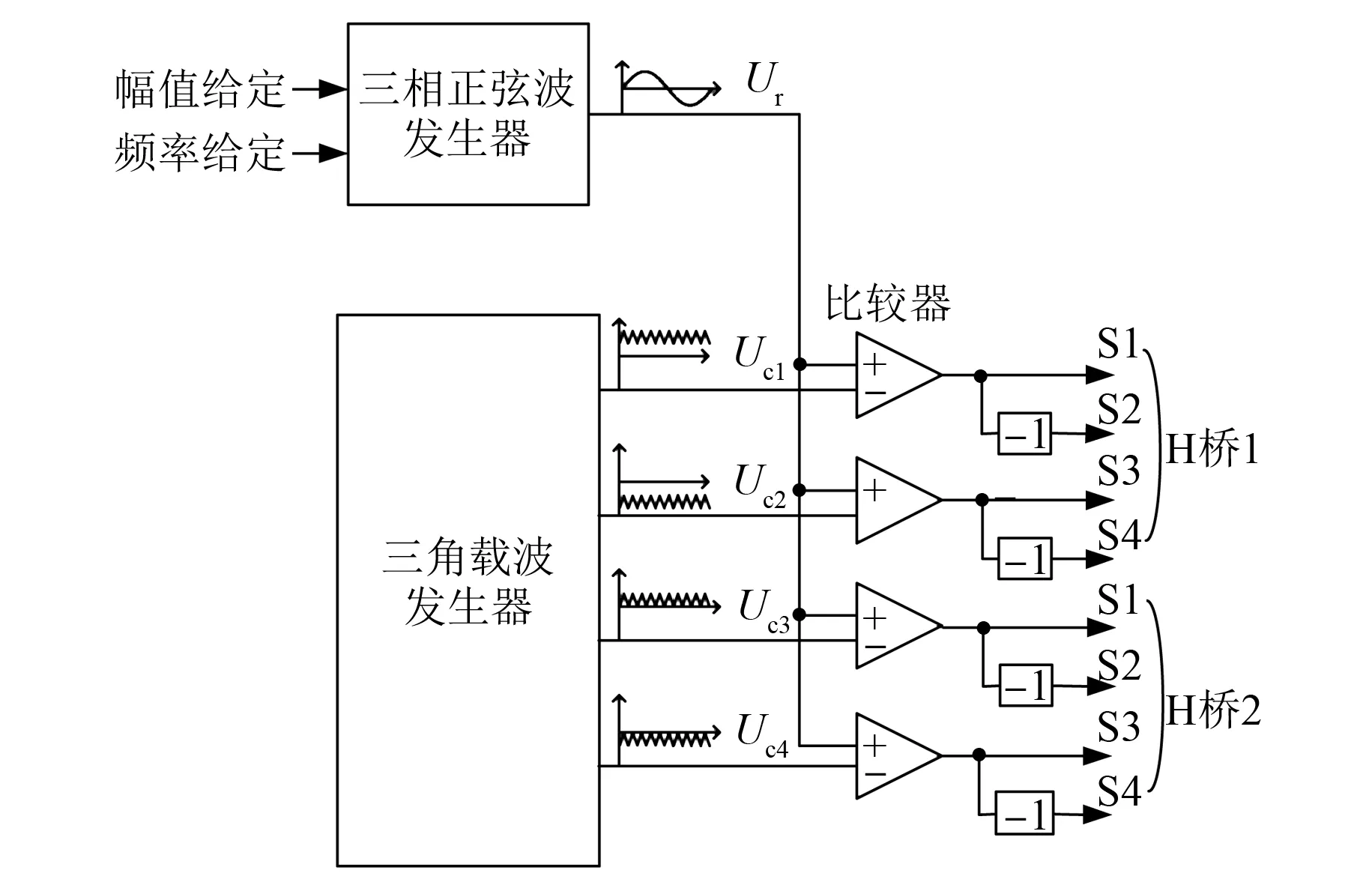
2 三角载波层叠PWM的数字实现方法

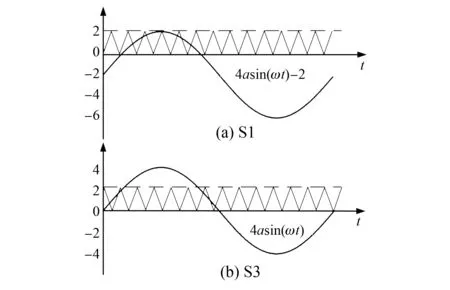
3 试验验证
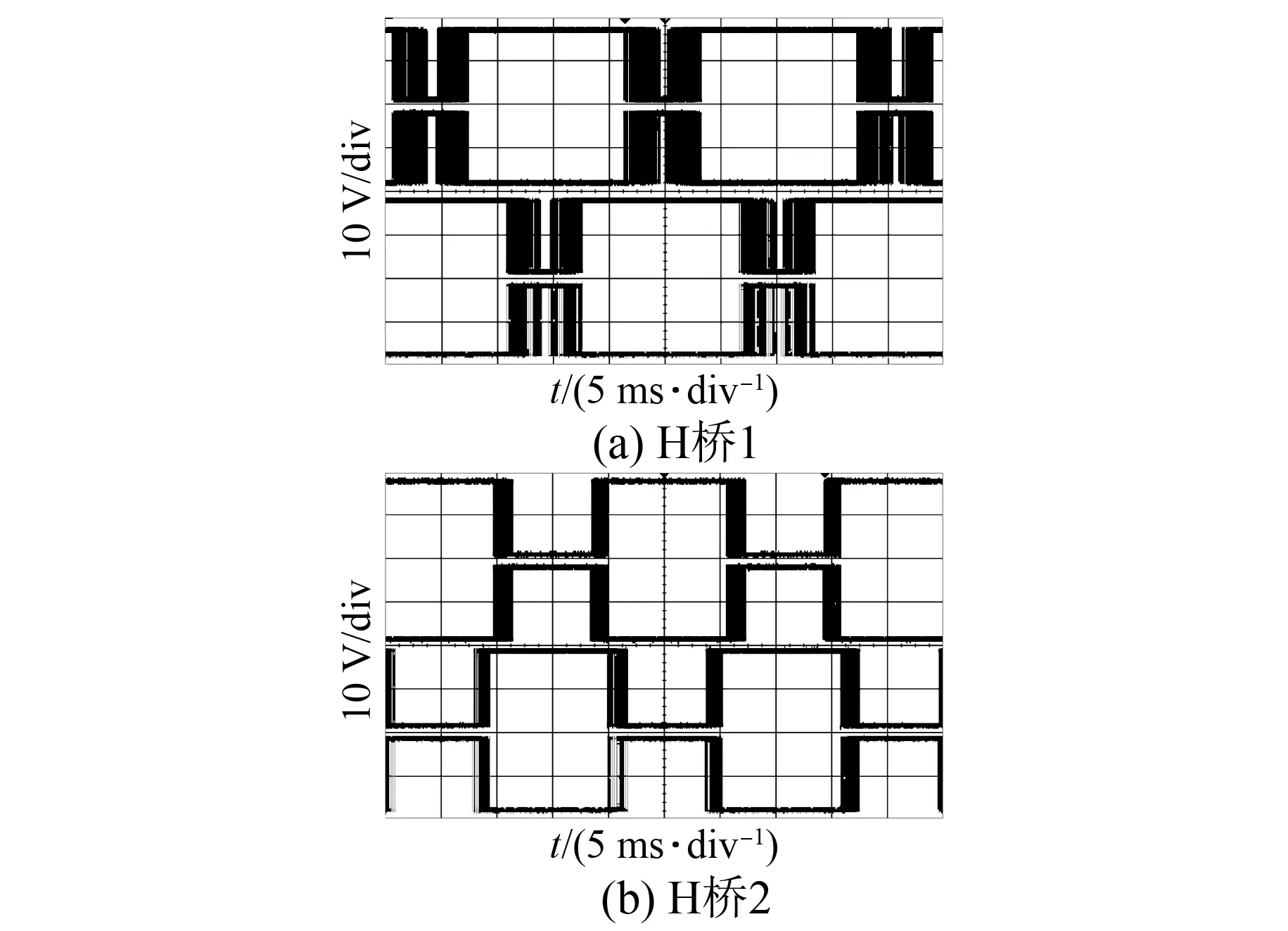

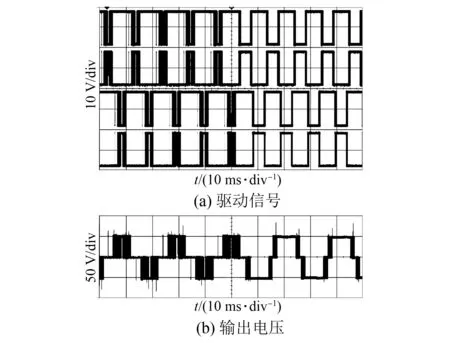
4 三角载波层叠PWM存在的问题及其优化


5 结 语

