行走在以学为中心的课堂边上

[摘要]随着新课程改革的进行,小学各学科的教育教学都在发生着明显的变化,进而提出了以学生为中心的教学理念,更加凸显了学生的课堂主体地位和教师在教学中的引导作用。以《三角形三边关系》为实践载体,在构建以学为中心的课堂的过程中,分别从小组合作探究学习、问题导学活动导思、任务驱动以学定教三个层次展开教学,层层递进。
[关键词]以学为中心;探究学习;以学定教
以学为中心是对课堂实质言简意赅的表达。在践行过程中,教师要努力促使学生向文本、同伴和老师学习,同时根据进程调整应对,评价成果。四年级《三角形三边关系》一课,意图让学生经历数学探究活动了解三边关系,发展观察操作对比抽象等能力,并渗透分类集合对应等数学思想方法。几年间,笔者三次同课异构,让学生成为学习的主人是始终不变的努力方向。
第一次实践:小组合作,探究学习
首次执教《三角形三边关系》时关注课堂从形式到内容的变更,尝试教与学的双向变化。学生六人一组开展三项操作活动,他们尝试自主、合作、探究的新型学习方式,通过动手、动眼、动口、动脑主动获取知识。
活动一:研究不能围成三角形的情况
测量三根小棒的长度并记录数据,看能否围成三角形,想想为什么(课堂上提供了两组不同长度的小棒,分别是2cm、5cm、8cm和4cm、4cm、8cm。每一组学生都只能接触到其中一组数据。)学生用“2+5<8”和“4+4=8”表述无法围成三角形的理由,得出“如果两根较短小棒的和小于或等于第三根小棒,就不能围成三角形”的结论。
活动二:研究能围成三角形的情况
学生提出猜想:也许两根较短小棒的和大于第三根小棒,就能围成三角形。他们各自想办法,有人指出可以换掉不合适的那根小棒。他們决定选择一根替换三根小棒中的一根再试试看能否围成三角形,并用式子表述理由。学生充分操作之后汇总数据总结出“只要两根较短小棒的和大于第三根小棒,就能围成三角形”,并验证了猜想。
【反思】师生的角色转变是一种觉醒。教师原来是把持话语权的主角,现在退而组织学生的数学活动,尽管探究行动在事先设定的框架内开展,但学生分工合作分享交流,课堂效果很好。同时我也考虑两个问题:第一,将不能围成三角形的两种情况剥离出来探究,这一安排是否合适?第二,活动的设置是不是可以多考虑学生可能的思路和需要重新设计?
第二次实践:问题导学,活动导思
再次琢磨时,我围绕发展学生的空间观念和推理能力的主旨,以问题导学、活动导思为主线组织教学,从量到摆再到算逐步推进。
问题一:我们可以用什么方法研究三角形的三边关系?
学生如预设中表示或量或摆,教师因势利导设置两层活动:
第一层:测量三角形边的长度,观察有否规律?(单单观察数字,学生发现不了隐含的关系,只能借助摆小棒进一步求解。)
第二层:从四根小棒(3cm、3cm、6cm、7cm)中选择三根摆一摆,看看能否围成三角形,并记录。
学生在讨论中得到“3+3=6,3+3<7,3+6>7”三个式子,慢慢靠近“必须两根小棒长度和大于第三根小棒时,才可以摆成三角形”的结论。
问题二:从小棒长度关系来看,三角形的三边可能存在什么关系?
学生回到之前测量过的三角形去寻找答案,逐渐梳理出几个不等式,并得出:三角形任意两边之和大于第三边。
问题三:三条长度分别是3cm、6cm、2cm的线段能不能围成三角形?
通过计算发现只要满足“两条较短边之和大于第三边”即可围成三角形。探究活动从直观小棒至抽象式子,知识建构向符号化的方向纵深行进。
【反思】纵观全课,课堂更多考虑了学情因素,三个问题在层层递进中逻辑严密。学生主动操作、辩论解疑,既培养了推理能力,又发展了空间观念。在活动开展过程中,教师用问题掌控课堂,学生量摆算时少了主观能动性。
第三次实践:任务驱动,以学定教
第三次设计此课恰逢教材改编,我选择完全回归文本,让学生带着任务自学,基于经历而积累经验,在课堂交流中基于需要,着力帮助学生完成自主建构。
一、布置自学
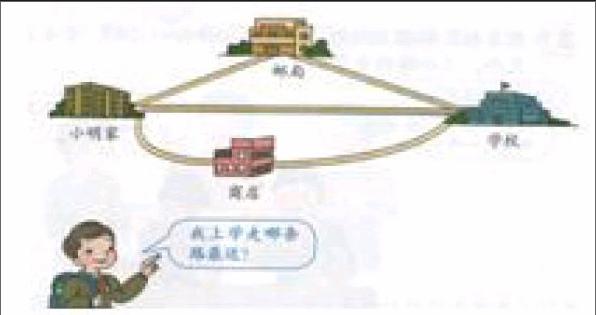
1.自学课本62页例3,小明家到学校有几条路?哪条路最近?为什么?
2.参照例4提供的数据(单位:cm) ,剪出四组纸条分别摆三角形。思考为什么有的数据可以摆成三角形,有的却不能?
A.6、7、8 B.4、5、9 C.3、6、10 D.8、11、11
二、汇报交流
课始,学生引用文本“两点间所有连线中线段最短,这条线段的长度叫做两点间的距离”作答第一个问题。当给三段路赋长度值后,他们用“500+ 800>1000”加以解释,还用“1000+ 800>500”和“500+ 1000>800”说明小明从家去邮局和从邮局到学校的最短路程,表示可以用“三角形任意两边之和大于第三边”阐述两点间直线距离最短的原因。
自学问题二分三个阶段展开汇报:
1.作品展示
首先展示的是用“6、7、8”和“8、11、11”围成的三角形,引导学生认识三条线段首尾相接视为围成三角形。大家一致认为因为3+6<10,所以3cm和6cm两条线段相接“够不着”10cm的那条(图1)。在“4、5、9”组合的展示中(图2、图3、图4),摘录如下:
2.数据分析
至此,课堂交流自然锁定“到底是什么因素决定三条线段可以围成三角形”,学生意识到“是线段之间的长度关系决定的”,学生整理出四组式子进行对比分析,发现当两条短边之和不能大于第三条边时,就围不成三角形。
3.解释应用
一道开放式问题用以拓展提升:改变3cm、6cm、10cm一组中的10cm纸条的长度(取整厘米数),再与3㎝、6㎝的纸条围成一个三角形,有几种修改方案(可剪可摆可算)?学生计算得出长度取值范围是8cm到4cm。教师借助工具绘图,让学生感受到当数据改成5cm、4cm时,原有6cm长的线段就变成了三角形里的最长边了,用以判断的长度关系也要随之修正。
【反思】在自学任务驱动下,呈现更多学的行动和思的较量。教师总是担心学生看书之后都懂了教师还怎么教,其实很简单,真懂了就不用教,没真懂就好好琢磨如何以学定教,一知半解比蒙昧无知起点更高,终点更远。
行走在以学为中心的课堂边上,不同思考有不同收获,让学生立于课堂是首要考量,离于课堂仍有力后续发展是核心任务。
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准[S].北京:北京师范大学出版社,2012.
[2]钟建林,林武.小学数学专题式教学导引[M].福州:福建教育出版社,2012.
(责任编辑 冯 璐)

