一种雷达主瓣欺骗干扰抑制算法*

董玮，李小波，单凉，王瑜

( 电子工程学院， 安徽 合肥 230037)

一种雷达主瓣欺骗干扰抑制算法*

董玮，李小波，单凉，王瑜

( 电子工程学院， 安徽 合肥 230037)

针对单通道雷达受到主瓣干扰，提出了一种基于多周期采样的抗主瓣干扰方法。首先针对距离密集假目标欺骗干扰，建立了基于多脉冲重复间隔(paulse repeat interval)采样的抗主瓣欺骗干扰模型并对其可行性进行证明，然后对信号源个数进行估计，最后借助提出的盲源分离方法将干扰信号与目标回波信号分离，达到抗干扰效果。理论分析和仿真表明，该方法具有较好的分离效果及干扰抑制能力。

多PRI采样；抗主瓣干扰；距离密集假目标；盲源分离；脉压检测；单通道

0 引言

近年来，随着信息技术的不断发展，雷达在电子战中的生存环境也日趋复杂。面对高强度、多样式的复杂电磁干扰环境，人们提出了各种抗干扰方法，如旁瓣匿影、旁瓣对消、低旁瓣等。但是在面对现有的压制干扰主要从主瓣进入雷达天线时，旁瓣抗干扰方法几乎失效[1-2]。

盲源分离方法首先在20世纪80年代被提出，该方法在无线通信、雷达信号处理、语音信号处理等领域应用广泛。在雷达抗干扰领域，运用盲源分离能够将目标回波信号与干扰信号分离来达到抗干扰的效果[1]。在相控阵雷达体制中，文献[3-4]利用了基于特征矩阵近似的联合对角化盲源分离方法实现了雷达的抗主瓣干扰，但由于其算法需求解高阶累积量和2个特征分解，运算量较大，而且阶数较大时，容易产生误差。文献[5]将Fast ICA算法应用在雷达主瓣抗干扰上，实现了抗干扰效果。

目前雷达抗主瓣干扰研究都是在阵列信号处理基础上的多通道抗干扰，但随着通道数目增加，系统复杂度及成本会随之增大，而且独立通道间差异引起的误差也会增大。单通道雷达只有一个接收通道，系统简单且成本较低，适用范围较广，所以对单通道雷达抗干扰的研究有一定的实用价值。在单通道雷达抗干扰研究方面，由于先验知识较少且无法利用空域信息，目前在此方面的研究较少，文献[6]针对线性调频(linear frequency modulation, LFM)脉冲压缩引信欺骗干扰，提出一种基于适配解耦盲分离的方法，通过二次Strech变换构造虚拟通道来解决单通道的欠定问题，但其仅针对单个欺骗干扰进行简单讨论。文献[7]提出了一种基于相邻PRI采样的盲分离抗欺骗干扰方法，但其仅仅对单个欺骗干扰进行了讨论，且需要已知信号源个数作为先验条件，实用意义不大。本文主要针对于单通道雷达受到距离密集假目标干扰情况下，利用雷达脉冲回波的特点，将多个PRI采样代替空间上多通道采样建立虚拟通道，建立接收数据模型并对回波和干扰的可分离性进行分析，然后对信号源数目进行估计，最后借助盲源分离算法进行分离，达到抗干扰效果。仿真结果表明该算法有一定抗干扰效果。

1 问题描述

1.1 信号接收模型

设定干扰场景为伴随式干扰，当干扰信号和目标回波信号从不同方向进入雷达主瓣，在时、频域存在混叠，常规的滤波方法不能有效抑制。假设只有一个接收通道，雷达信号为LFM信号。首先简单考虑一个目标源信号和一个干扰源发出的干扰信号的混合信号，经过未知信道传输后，得到一路线性混合信号。

发射信号为LFM信号

(1)

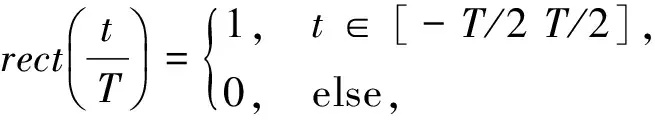
采用DRFM相位量化技术[8]，干扰信号为

(2)

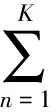
为保证有效干扰，干扰时延应满足

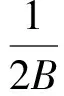
(3)

式中：B为信号频谱宽度，1/(2B)代表雷达时间分辨率，当时延取值小于时间分辨率时，雷达检测干扰与目标回波为同一信号，失去干扰意义。T为雷达跟踪波门时间宽度，当时延取值大于跟踪波门时间宽度时，雷达无法准确跟踪干扰目标，此时干扰失效。

目标回波信号为

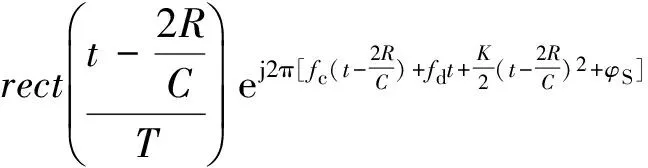
(4)

式中：fd为目标多普勒频移;a为回波信号幅度;R为雷达与目标距离。

采用相邻PRI接收信号处理模型，设第1个PRI的回波信号为S1(t)，则

(5)

s1(t)=a11s′(t).

(6)

同理，第1个PRI内的干扰为

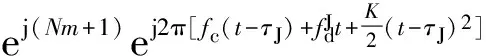
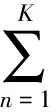
(7)

对于相邻PRI来说，其相对的时延差和多普勒频移变化等相对较小，可以忽略。下面给出证明：

为量化讨论，取PRI在1～10kHz范围内，目标速度为700m/s，采样频率2～10MHz。一个PRI内目标距离变化为0.07～0.70m，则相邻PRI内目标相对时延τ为 4.6×10-10～4.6×10-9s，而雷达系统采样时间TS为1×10-7～5×10-5s。显然，TS≫τ，故可认为τ未发生变化。但当PRI个数太多时，仅能满足TS>τ且τ不能被忽略，故为了保证算法的有效性，此方法适应范围限定在信号源个数较少、PRI个数较少的情况，且随着选取的PRI个数增多，单个PRI间的时延差和多普勒频移增大且目标运动可能会跨越距离单元，使算法的性能变差甚至失效。

综上，对第2个PRI，有s2(t)=a12s′(t)；相应，第2个PRI内干扰为J2(t)=b22J′(t)。于是，相邻脉冲回波周期的接收信号可表示为

(8)

将式(8)写成线性瞬时混合ICA模型为

X(t)=AS(t)+n(t),

(9)

式中：X(t)=(x1(t),x2(t))T；S(t)=(s′(t),J′(t))T；信号混叠矩阵A=(a11,b21;a12,b22)，通道加性噪声向量n(t)=(n1(t),n2(t))T。

1.2 信号可分离性讨论

目标回波是我方雷达系统发射经过目标反射后进入雷达接收机的回波信号，欺骗干扰是敌方干扰机接收到发射信号后经过其内部系统处理，再由干扰机发射的一类信号，信号本身带有干扰机系统的特征，故可以认为目标回波和欺骗干扰是由2个独立的系统发出的。而且干扰背景为伴随式干扰，干扰和信号从不同路径进入主瓣，因此可以在一定程度上认为二者相互独立[9]。下面从相关性的角度分析干扰和回波：

选取密集假目标中任意一个干扰信号为

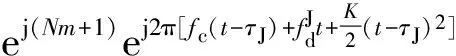
(10)

回波信号为

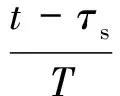
(11)

则相关系数

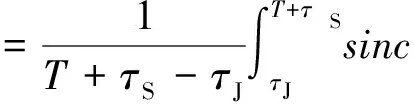
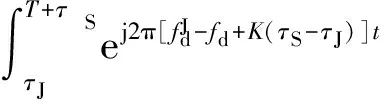
(12)

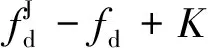
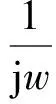
j(sin(T+τS)w-sin(τJw))].

(13)

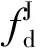
对接收数据矩阵白化后的四阶互累积量矩阵为[7]

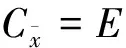
(14)

由式(14)可知，其主对角线代表干扰与回波的四阶累积量，负对角线表示干扰与回波的四阶互累积量，所以干扰与回波的四阶累积量同样不相关。故在使用基于高阶累积量的盲源分离算法时，能够分离回波和干扰。同理可证，对同一干扰机在同一回波周期内产生的任意一个欺骗干扰，其与回波信号间的四阶累积量都可以认为相同，因此目标回波和干扰间可分。

2 信号源数目估计

信号源个数估计的方法比较成熟，主要有基于信息论准则的AIC和MDL方法、基于盖尔圆盘定理的方法以及基于奇异值分解的方法。本文采用基于信息论准则的MDL方法，能对信号源数目作出较为准确的估计。为保证信号源数目估计的准确性，应在保证数据模型有效的情况下，选取尽量多的PRI构成接收数据矩阵以保证观测数据维数大于信号源数。

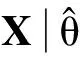
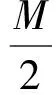
(15)

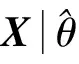
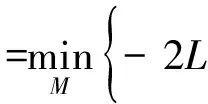
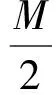
(16)

由MDL准则得到的估计是信号源数目真实值的一致估计；而AIC准则得到的估计是信号源数目真实值的过估计，所以本文采用MDL准则作为信号源数目估计。

3 基于高阶累积量的盲源分离算法

特征矩阵联合对角化(JADE)方法[10]最早由Cardoso提出，其引入了高阶累积量矩阵，并对其进行特征值分解来实现混合矩阵的估计。相对于基于峭度、负熵和互信息等[11-13]对野值敏感，鲁棒性差且受高斯噪声影响很大等缺点，由于于高斯白噪声的高阶累积量为0，因此本算法对高斯过程具有不敏感性，在一定程度上能够抑制通道白噪声的影响，符合本文的要求。JADE算法首先对接收数据进行预白化处理如下：

接收数据的零延迟相关矩阵估计为

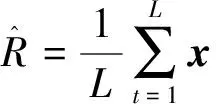
(17)

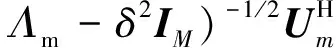
(18)

z=Wx.

(19)

给定任意一个非零矩阵T=(τij)m×m，定义矩阵N=Qz(T)=(nij)m×m，有

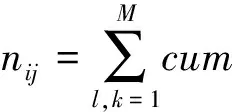
(20)

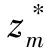
(21)

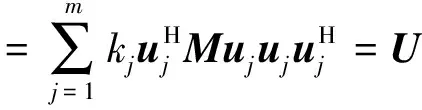
(22)

式中：uj为酉阵的第j列；kj为源信号的四阶累积量。

对样本白化后的四阶累积量矩阵进行特征值分解为

Qz(T)=(UP)(PHΛTP)(UP)H=VΣVH，

(23)

式中：P为置换矩阵；Σ为对角阵。即U的估计V为V=UP。

(24)

4 仿真分析

4.1 算法有效性验证

为了检测本算法的可行性和有效性，下面模拟主瓣欺骗干扰进行仿真实验。实验中为单个阵元接收信号，设置一个目标源和一个干扰源，发射信号为LFM信号，信号脉宽100 μs，带宽1 MHz，采样频率4 MHz，一个PRI采样点为4 000个；密集假目标干扰信号为经DRFM调制的转发式干扰，密集假目标具体设置为每隔20 μs一个，共设置45个，达到对目标回波信号在时域和频域的完全覆盖，a1,b1,a2,b2分别取0.75,1.2,0.87,1，信号及干扰初相为[-π,π]的均匀分布。这里设置干信比JSR在0～40 dB范围内(JSR定义为干扰信号能量与回波信号能量之比)，信噪比SNR初值为10 dB(SNR定义为信号能量与通道噪声能量之比)。

当干信比为20 dB,信噪比为10 dB时，2个PRI的接收数据直接脉压波形如图1c)所示，可见无法分辨哪个脉压尖峰是信号回波，此时主瓣受到严重干扰，已不能正常工作。图2为算法分离后脉压波形图，可以看出回波信号被有效分离并脉压出来，尖峰信噪比约13 dB。

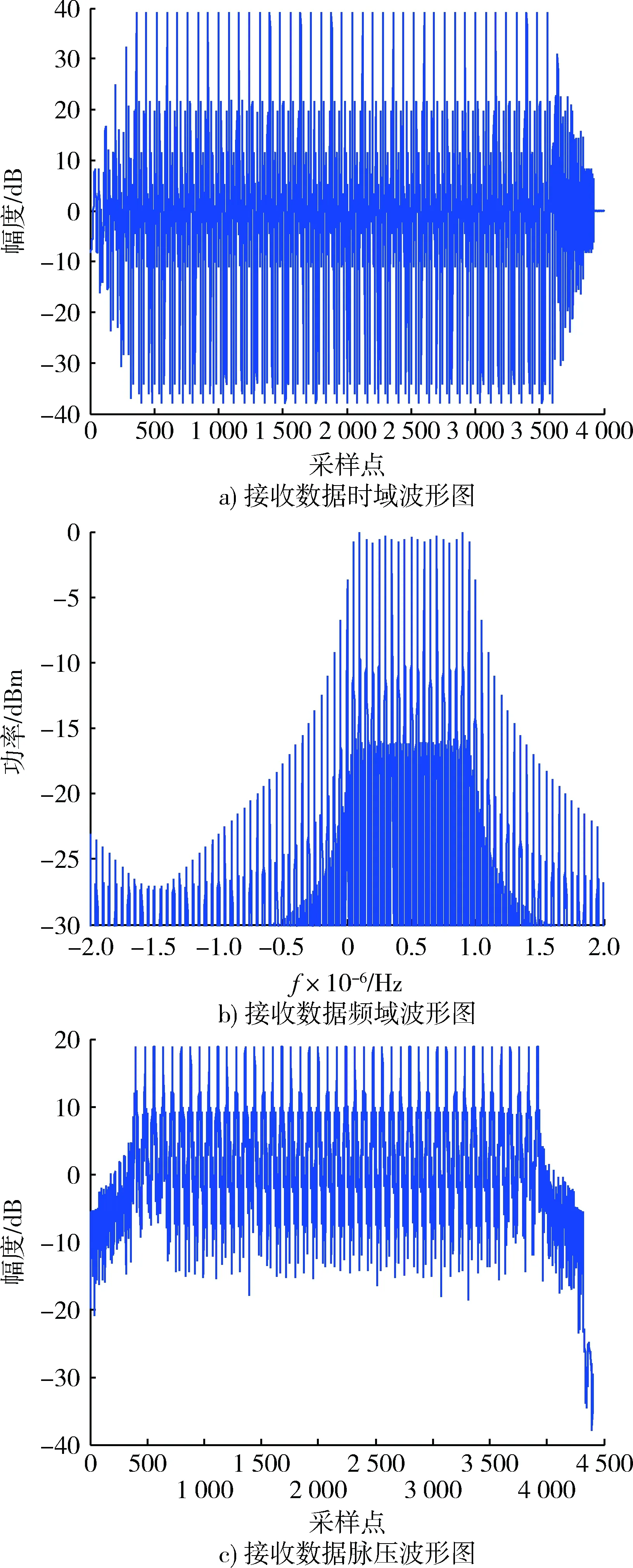
图1 接收数据波形图Fig.1 Received data waveform

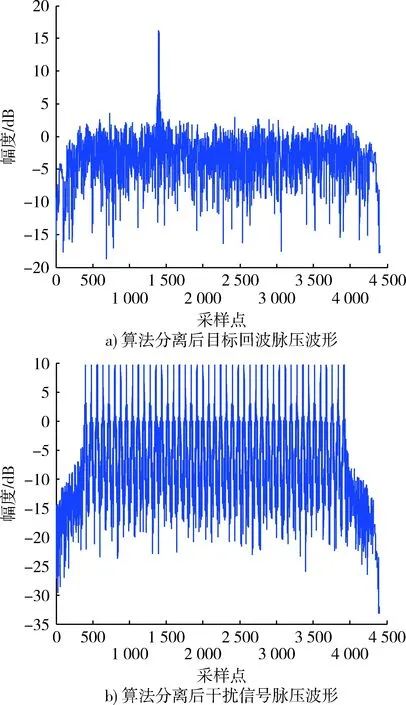
图2 算法分离后目标回波与欺骗干扰脉压图Fig.2 Target echo and deception jamming pulse pressure after the algorithm separation

当改变信噪比至20 dB，干信比至30 dB时，单个PRI内接收数据脉压及算法分离后目标回波及干扰脉压波形如图3所示。可以看出，此时分离后目标回波的脉压尖峰信噪比约为22 dB，干扰信号脉压尖峰被抑制约10 dB，所以随着信噪比的升高，算法对干扰的抑制能力进一步提升，而干信比的升高对算法本身影响不大，表明算法对干信比不敏感。这是因为本文算法将干扰和信号看作2个独立的信号源，依据它们的独立性进行分离，而盲源分离算法本身受通道高斯噪声的影响较大。故算法性能会随着信噪比的升高而显著提升。

图3 SNR=15 dB, JSR=30 dB时分离效果图Fig.3 Separation effect of SNR=15 dB, JSR=30 dB

4.2 算法性能分析

为了定量分析本文算法的分离性能，本文引入源信号和分离信号的相似系数偏差C以及分离后干扰抑制比2个算法性能指标[14-15]。

(1) 定义相似系数偏差C=1-ζij，其中ζij为相似系数，且

ζij=ζ(yi,sj)=

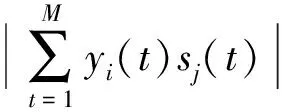
(25)

当ζij为1时，有yi=csj，c为常数即允许分离信号和源信号仅仅在幅度上有差异；当ζij为0时，二者相互独立。也就是说，当相似系数偏差越趋近于0时，分离性能越好。

当JSR固定为20 dB不变，SNR取0～20 dB变化时，回波信号与干扰信号的相似系数偏差曲线如图4所示。可以看出，随着信噪比的提高，本文算法分离效果越来越好，即使在信噪比较低的情况下，回波信号恢复相似系数依然能达到90%左右。但随着信噪比的降低，其性能下降速度也逐渐加快，这与理论推导相吻合，因为盲源分离算法本身对噪声较为敏感，当信噪比下降到一定程度时，盲源分离算法甚至会失效。

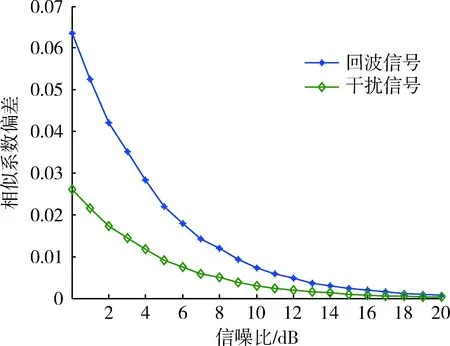
图4 目标回波与干扰相似系数偏差曲线Fig.4 Target echo and jamming similarity coefficient deviation curve

表1为当信噪比SNR=10 dB时，干信比分别为10，20，30 dB时的相似系数矩阵，可以看出，随着干扰强度增大，本文算法仍然能较好地将信号和干扰分开，且信号恢复性能较好。

表1 相似系数对比

(2) 定义干扰抑制比为γ

(26)

式中：PJ为干扰功率；PS+N为信号和噪声的合成功率。

因为算法分离前，回波信号完全淹没在密集假目标干扰中，且经过脉压后尖峰被假目标干扰遮盖(如图1c))，导致无法准确识别出回波信号。定义分离后信号脉压峰值增益为算法的干扰抑制比。分离后干扰抑制比越高，表示算法的抗干扰性能越好，更利于对回波信号的后续处理。

图5给出了JSR分别为20 dB和30 dB时算法干扰抑制比与接收数据信噪比的变化，可以看出随着信噪比升高，算法的抗干扰性能提升且受干信比影响不大。

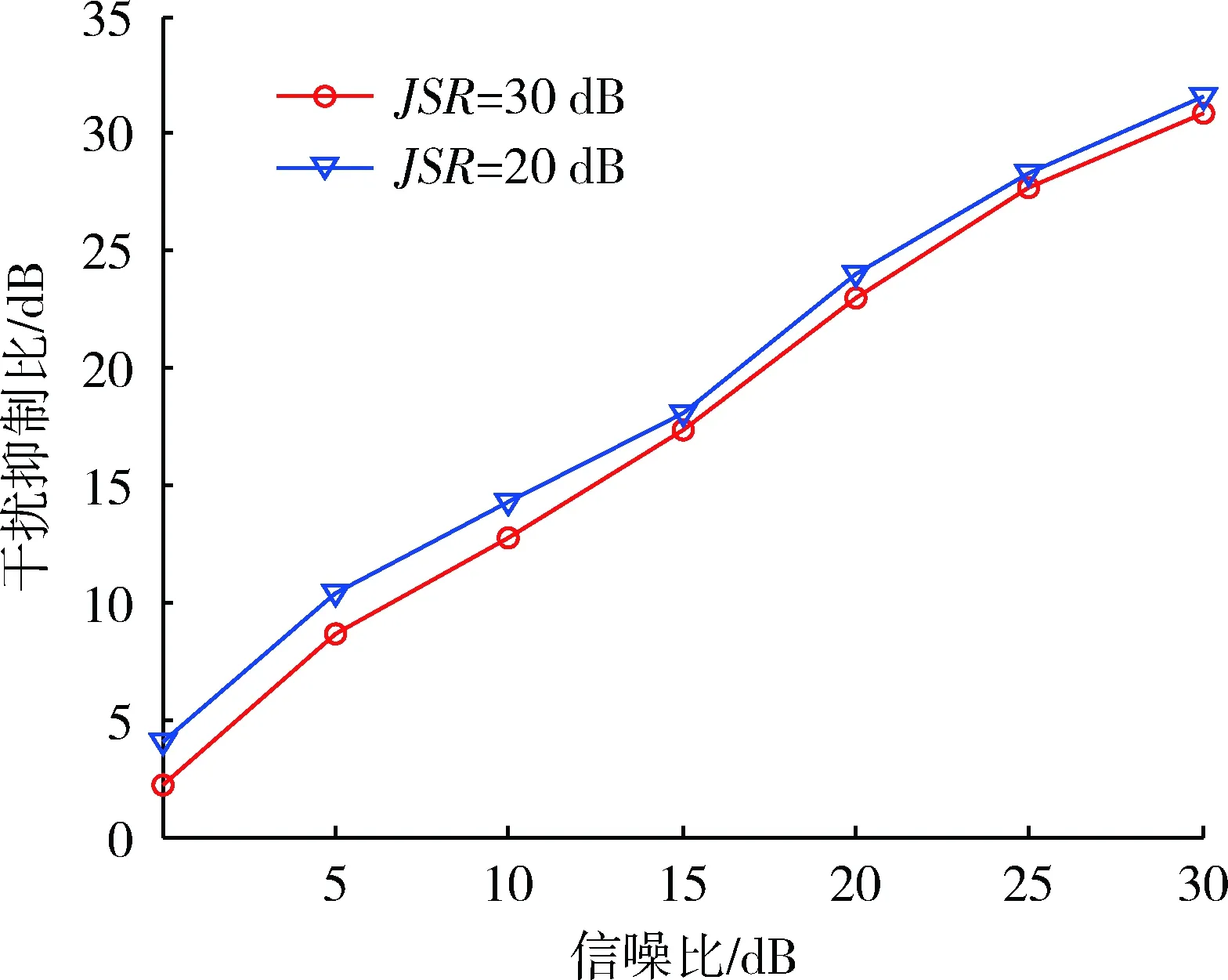
图5 回波信号干扰抑制比Fig.5 Echo signal interference suppression ratio

图6为当SNR为10 dB，JSR为20 dB时，随着虚拟通道数(PRI个数)的增加，算法分离后的回波信号相似系数变化情况。可以看出，在保证相邻PRI间隔内目标不产生距离单元跨越时，即保证回波信号在相邻PRI的稳定性情况下，虚拟通道个数越多，算法分离性能越好。这是因为在保证算法有效的情况下，虚拟通道个数越多，信号的有效信息量越大。对盲源分离算法来说，由欠定模型成为正定模型进而变为超定模型进行分离，其信息量大大增加，算法分离效果必然提高。

图6 虚拟通道数对算法性能的影响Fig.6 Effect of the number of virtual channels on the performance of the algorithm

5 结束语

单通道雷达接收系统相比多通道系统来说，有硬件设备少、成本较低、适用范围较广等优势，且能够有效避免通道间的互耦、幅相不一致等问题，所以对单通道雷达抗干扰的研究十分有价值。但是单通道系统对信号处理算法要求较高，常用的方法几乎失效。

本文在单通道情况下，针对伴随干扰中的距离密集假目标主瓣干扰问题，提出一种利用多个PRI采样来构造虚拟通道解决单通道欠定问题的方法。然后通过高阶累积量对干扰和回波信号的可分离性进行分析及信号源个数估计，最后通过基于高阶累积量的盲源分离算法将信号和干扰分离，进而达到抑制干扰的目的。理论分析和仿真结果表明，该方法在满足一定信噪比的情况下能够有效抑制干扰。但本文算法仅在伴随式干扰背景下针对距离密集假目标干扰进行分析，实际复杂电磁环境下多种干扰样式并存，如何在复杂干扰环境下提出一种全面有效的抗干扰方法是未来值得研究方向。

[1] 王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32(10): 46-49． WANG Jian-ming, WU Guang-xin, ZHOU Wei-guang. A Study on Radar Mainlobe Jamming Suppression Based on Blind Source Separation Algorithm[J]. Modern Radar, 2010, 32(10):46-49.

[2] KAI B Y, DAVID JM. Adaptive Digital Beam Forming for Preserving Monopulse Target Angle Estimation Accuracy in Jamming[C]∥Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop. Cambridge, MA: IEEE Press, 2000: 454-458.

[3] 李荣峰, 王永良, 万山虎. 主瓣干扰下自适应方向图保形方法的研究[J]. 现代雷达, 2002,24(3): 50-55. LI Rong-feng, WANG Yong-liang, WAN Shan-hu. Research of Reshaping Adapted Pattern under Mainlobe Interference Conditions[J].Modern Radar, 2002, 24(3):50-55.

[4] 苏保伟, 王永良, 李荣峰，等. 阻塞矩阵方法对消主瓣干扰[J]. 系统工程与电子技术, 2005, 27(11): 1830-1832. SU Bao-wei, WANG Yong-liang , LI Rong-feng, et al. Mainlobe Interference Canceling Method via Block Matrix[J]. Systems Engineering and Electronics, 2005, 27(11):1830-1832.

[5] 周青松, 王文涛, 王珽,等. 盲源分离算法和FRFT联合抗雷达主瓣干扰技术研究[J]. 信号处理, 2015, 31(8): 1004-1011. ZHOU Qing-song, WANG Wen-tao, WANG Ting, et al. A Study on Radar Mainlobe Jamming Suppression Technique Based on Method of BSS-FRFT Union[J]. Journal of Signal Processing, 2015, 31(8):1004-1011.

[6] 尹洪伟, 李国林, 路翠华. 基于盲分离的单通道LFM引信欺骗干扰抑制[J]. 电讯技术, 2014,54(11):1475-1481. YIN Hong-wei, LI Guo-lin, LU Cui-hua. Signal-Channel LFM Fuze Deception Jamming Suppression Based on BSS[J]. Telecommunication Engineering, 2014, 54(11):1475-1481.

[7] 罗双才, 唐斌. 一种基于盲分离的欺骗干扰抑制算法[J]. 电子与信息学报, 2011, 33(12):2801-2806. LUO Shuang-cai, TANG Bin. An Algorithm of Deception Jamming Suppression Based on Blind Signal Separation[J]. Journal of Electronics and Information Technology, 2011, 33(12):2801-2806.

[8] GRECO M, GINI F, FARINA A. Radar Detection and Classification of Jamming Signals Belonging to a Cone Class[J]. IEEE Transactions on Signal Processing, 2008, 56(5):1984-1993.

[9] RAMIREZ D, SCHREIER P J, VIA J, et al. GLRT for Testing Separability of A Complex-Valued Mixture Based on the Strong Uncorrelating Transform[J]. IEEE International Workshop on Machine Learning for Signal Processing, 2012, 248(6):1-6.

[10] CARDOSO J F, SOULOUMIAC A. Blind Beamforming for Non-Gaussian Signals[J]. LEE Proceedings F, 1993, 140(6):362-370.

[12] V. D S A. Frontiers of Research in BSS/ICA[J]. Neurocomputing, 2002, 49(3):7-23.

[13] 尹洪伟,李国林,路翠华. 单通道伪码引信欺骗干扰分离算法[J]. 探测与控制学报,2015,37(6):31-34. YIN Hong-wei, LI Guo-lin, LU Cui-hua. Separation Algorithm of Single Channel PN Fuze Deception Jamming[J]. Journal of Detection and Control, 2015, 37(6):31-34.

[14] ZHAO Y, HE H, MI J. Noisy Component Extraction with Reference[J]. Frontiers of Computer Science Selected Publications from Chinese Universities, 2013, 7(1):135-144.

[15] HUANG D S,MI J X.A New Constrained Independent Component Analysis Method[J]. IEEE Transactions on Neural Networks, 2007, 18(5):1532-1535.

An Algorithm of Radar Mainlobe Deception Jamming Suppression

DONG Wei, LI Xiao-bo, SHAN Liang, WANG Yu

(Electronic Engineering Institute,Anhui Hefei 230037, China)

A suppression method is proposed based on multi-period sampling and BSS algorithm. At first, the model of range dense false target mainlobe jamming suppression based on multi-period sampling is given and proved. Then the number of signal source is estimated. The target echo signal and interference signal are separated by BSS algorithm, which finally achieves jamming suppression effect. Theoretical analysis and computer simulation demonstrate that the proposed method has a good performance on both the mixture signal separation and the interference suppression.

multi-PRI sampling; main lobe jamming suppression; range dense false target; blind source separation(BSS); pulse-compression detection; single channel

2016-04-19；

2016-06-21 作者简介：董玮(1992-)，男，江西九江人。硕士生，主要研究方向为雷达信号处理、盲信号处理。

10.3969/j.issn.1009-086x.2017.02.033

TN972；TP301.6；TP391.9

A

1009-086X(2017)-02-0209-08

通信地址：230037 安徽省合肥市黄山路460号电子工程学院502教研室 E-mail：15609699135@163.com