一种新的基于自适应分数阶的活动轮廓模型

张桂梅 徐继元 刘建新

1(江西省图像处理与模式识别重点实验室(南昌航空大学) 南昌 330063)2 (西华大学机械工程学院 成都 610039) (guimei.zh@163.com)

一种新的基于自适应分数阶的活动轮廓模型

张桂梅1徐继元1刘建新2

1(江西省图像处理与模式识别重点实验室(南昌航空大学) 南昌 330063)2(西华大学机械工程学院 成都 610039) (guimei.zh@163.com)

区域可调拟合(region scalable fitting, RSF)活动轮廓模型在分割弱纹理、弱边缘图像时，优化易陷入局部极小导致曲线演化速度缓慢；同时该模型中的局部拟合项为高斯核函数，导致目标的边界模糊，影响分割精度.针对该问题，提出了一种基于自适应分数阶的活动轮廓模型，用于图像的分割.首先将全局G-L(Grünwald-Letnikov)分数阶梯度融合到RSF模型中，以增强灰度不均匀和弱纹理区域的梯度信息,从而提高对曲线初始位置选择的鲁棒性，并提高了图像分割的精度和速度；然后用双边滤波函数替换局部拟合项中的高斯核函数，解决了高斯核函数在演化过程中造成的边界模糊问题;最后根据图像的梯度模值和信息熵构建自适应分数阶阶次的数学模型，并计算出最佳分数阶阶次.理论分析和实验结果均表明:提出的算法可以用于灰度不均匀和弱纹理、弱边缘区域的图像分割，并能根据图像的特征自适应计算最佳分数阶阶次，避免曲线演化陷入局部最优.用多幅图像进行实验，得出该方法的分割精度和分割效率都有较大提高.

Grünwald-Letnikov分数阶；自适应分数阶；RSF模型；活动轮廓模型；图像分割

医学图像分割是医学图像分析应用的基础，当前的临床辅助诊断、图像引导的外科手术和放射治疗中，医学图像分割技术显示出越来越重要的临床价值[1].但由于医学图像在成像过程中，受到电磁环境、成像设备以及人体结构的差异等客观因素的影响，图像往往存在噪声、灰度不均匀、边缘模糊、纹理结构不清晰等特点.在分割这类图像时，传统的分割方法得到不理想的分割结果.

近年来，基于活动轮廓模型的分割方法在医学图像中得到广泛应用[2-9].活动轮廓模型主要分为基于边界和基于区域的分割模型.其中基于区域的分割模型，对噪声和模糊具有较强的鲁棒性，因此相比于基于边界的分割模型应用更为广泛，本文主要研究基于区域的活动轮廓模型.2008年Li等人[3]提出了区域可调拟合(region scalable fitting， RSF)的分割模型,该模型能较好地分割灰度不均匀的图像，同时还能避免演化曲线的重新初始化，极大地提高了分割的效率,但是RSF模型在分割弱纹理、弱边缘图像时，由于仅仅利用局部信息以及在拟合项中使用高斯核函数，演化曲线易陷入局部最优，无法得到正确的分割结果;针对该问题，文献[4]结合图像的边界信息和区域信息，运用贝叶斯定理，提出自适应分割速度拟合项和概率加权项,该方法可以自行确定收缩方向以及分割速度，较好地完成了弱边缘图像的分割，但是该方法对演化曲线初始位置的选择仍较敏感，且对于弱纹理和灰度不均匀图像的分割效果欠佳;文献[5]提出了一种基于边缘和区域信息的先验水平集图像分割方法，该方法首先将图像的区域信息融入基于边缘的水平集方法，然后将其与形状先验信息结合，解决了被遮挡目标以及与背景相似的目标分割问题;文献[6]基于局部灰度均匀图像的聚类属性，定义了一个局部聚类方程用于对灰度不均匀区域进行均匀校正，对灰度不均匀图像能够快速地完成分割，但是该方法容易造成过分割现象;文献[7]提出了一种基于区域显著性的活动轮廓模型，将图像分割问题与图像视觉特性相结合，实现了活动轮廓模型对图像的自适应分割.但对于结构复杂的图像(如纹理丰富图像)分割效果不理想;文献[8]基于局部自适应阈值技术，提出了一个新的边缘探测方法，该方法提高了对肿瘤目标的分割能力，尤其是一些具有弱边界、边缘泄漏的肿瘤目标;文献[9]提出局部多尺度纹理结构对纹理部分进行像素级描述，此外还提出一个向量水平集，该方法对纹理丰富的自然图像有较好的分割结果.

分数阶微分具有在增强信号高频成分的同时，非线性地保留信号的中低频成分的特性，在数字图像处理中，这一性质被广泛地应用于保留图像的纹理细节和弱边缘[10-13].但是,对较为庞大的图像数据，由于拍摄相机的种类多样，外部拍摄环境的差异性，图像的质量总是参差不齐，若对所有图像都采用同一分数阶微分阶次处理，不能保证在不同环境下每幅图像处理的效果达到最佳.即使对于同一幅图像如何让图像中的不同区域去选取不用的阶次，并在各个区域处理的效果达到最佳，即分数阶阶次的自适应建模一直是个研究难题.文献[14]提出依据图像梯度信息和人眼视觉特性设计了分数阶微分算子掩膜用于图像增强，可以根据图像特征自适应选择合适的掩膜系数，实验结果表明：该方法对任意灰度图像可以得到连续变化的增强效果，接近于最佳分数阶微分增强效果，符合人们的视觉感受；文献[15]通过分析纹理特性建立幅值频率非线性联合指数模型，自适应选择分数阶微分阶次检测图像纹理细节，有效克服图像中纹理细节的变化，提出了一种自适应的分数阶微分的复合双边滤波算法，实验结果表明，自适应分数阶微分的复合双边滤波算法在图像滤波、去雾、细节增强等应用方面具有良好的效果；文献[16]提出了一种新的自适应活动轮廓模型的图像分割方法，但是该方法仅仅是在原有的拟合方程中增加了一项分数阶微分拟合项，分数阶阶次的选择仍然是通过人工选择；文献[17]将分数阶微分运用到全变分模型，在去噪效果更好的同时，保留了纹理细节和消除了块状负面效果，自适应的选择最佳的微分阶次是通过利用局部方差和小波变换得到的；文献[18]利用分数阶散度算子对CV模型[19]进行改进，同样提高了CV模型对弱边缘图像的分割能力，并且对噪声具有很强的鲁棒性，但是阶次的选择是通过大量的实验得到最佳的分数阶阶次，对演化曲线初始位置的选择较敏感，且对于灰度不均匀图像的分割效果不够理想.现有的分数阶活动轮廓模型不能有效分割灰度不均匀和弱边缘、弱纹理图像，且在分数阶最佳阶次的选择上缺乏真正的自适应.RSF模型能够较好地分割灰度不均匀的图像，但是局部拟合项中使用了高斯核函数，导致在拟合过程中，目标的边界变得模糊；同时当目标与背景灰度相近时，演化曲线的驱动力较小，因此在分割过程中容易陷入局部最优.针对这些问题，本文将分数阶微积分融合到RSF模型中，同时将原有的局部拟合项的高斯核函数用双边滤波替代，用于解决该模型在分割弱边缘、弱纹理图像时容易陷入局部最优的问题，并且根据图像的局部信息构造选择分数阶阶次的自适应函数，自动计算最佳的分数阶阶次.

本文主要有3点贡献：

1) 将全局G-L(Grünwald-Letnikov)分数阶梯度融合到RSF模型中，增强了灰度不均匀和弱纹理、弱边缘区域的梯度信息,提高演化曲线的驱动力，避免演化曲线在图像的弱边缘及纹理丰富区域陷入局部最优，从而提高对曲线初始位置选择的鲁棒性，并提高了图像分割的精度和速度：

2) 在RSF模型的局部拟合项中使用双边滤波函数，既考虑了像素空间位置的因素，又考虑了灰度值之间的差异性，避免边界弱化，从而提高了边界定位能力，解决了高斯核函数在演化过程中造成的边界模糊问题；

3) 根据图像的局部信息(如梯度幅值、信息熵)构建了自适应分数阶阶次的数学模型，计算最佳分数阶阶次，解决了人工寻找最佳分数阶阶次的费时费力问题.

1 相关理论

1.1 RSF模型

为了克服CV模型[19]不能分割灰度不均匀图像的缺点，Li等人[3]在CV模型的基础上，提出基于二元值拟合的活动轮廓模型，引入高斯核函数把原CV模型利用全局信息的平均值c1,c2变成具有局部性质的加权值f1(x)和f2(x).同时还定义一个新的符号距离函数，避免了曲线在演化过程中的重新初始化.RSF模型利用图像的局部灰度信息，较好地克服了传统基于区域的活动轮廓模型不能分割灰度不均匀图像的问题，提高了分割的效率.RSF的水平集能量方程如下：

(1)

其中，Kσ(x-y)是标准差为σ的高斯核函数，Mε1(φ)=Hε(φ)，Mε2(φ)=1-Hε(φ)，Hε为正则化的海氏(Heaviside)函数.式(1)的第1项为局部灰度拟合项，作用是驱动演化曲线运动目标轮廓；第2项为长度约束，约束演化曲线的周长；最后1项为符号距离函数，避免曲线在演化过程中重新初始化.f1(x)和f2(x)为局部平均值:

(2)

其中，i=1,2.

求能量方程的最小值可以通过求解能量泛函对应的Euler-Lagrange方程来实现.采用梯度下降法得到曲线的水平集演化方程：

(3)

其中，δε(φ)为正则化狄拉克(Dirac)函数.

(4)

其中，i=1,2.

RSF模型较大地提高了分割灰度不均匀图像的能力，但由于它仅仅利用图像的局部信息，易陷入局部最优，且对初始曲线的位置选择很敏感.在实际分割过程中，往往需要精心探测初始曲线的合适位置，从而较大地限制了RSF模型的应用.

1.2 分数阶微分定义

分数阶微分是整数阶微分的推广，目前经典的分数阶定义主要有3种[20]：R-L(Riemann-Liouville),G-L和Caputo.R-L定义和G-L定义在数值实现时可以以卷积形式进行运算，因此在信号处理领域中应用更为广泛；Caputo定义适用于分数阶微分边值问题的分析，所以多用于实际工程领域.而G-L定义在计算时较R-L定义更加准确[20]，因此我们从G-L定义出发，推导本文所需的分数阶微分算子.

若∀α∈(包括分数)，[α]为其整数部分.假设信号s(t),t∈[a,b](a0时，n至少取[α]，则分数阶微分定义如下

(5)

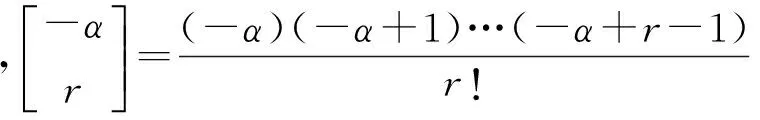
1.3 双边滤波定义

双边滤波是由Tomasi和Manduchi[21]提出一种非线性的滤波方法，它是结合图像的空间邻近度和像素值相似度的一种折中处理，同时考虑灰度相似性和空域信息，达到保边去噪的目的，具有简单、非迭代、局部的特点.双边滤波是在高斯滤波的基础上，增加了灰度差的影响，因为在模板内相邻像素之间的灰度差影响滤波结果.双边滤波定义如下：

(6)

W(i,j,k,l)为权重系数，由2部分组成：定义域核和值域核.定义域核为高斯滤波，定义为

(7)

值域核定义为

(8)

W(i,j,k,l)=G(i,j,k,l)*R(i,j,k,l)，

(9)

(10)

其中，σd为距离方差，σr为灰度差方差；i,j,k,l为像素点的坐标值；f(i,j),f(k,l)为像素点的灰度值；F(i,j)是滤波后的灰度值.从式(8)可以得出，在图像的边缘处，灰度差变化大，R(i,j,k,l)变小，则整个权重系数W变小，滤波效应减弱，保持了边缘.在图像平滑区域，灰度差变化很小，R(i,j,k,l)接近于1，则仅是高斯滤波.

2 本文算法

2.1 融合分数阶梯度的RSF模型

2.1.1 G-L微分掩膜构造

根据式(5)，若一元信号s(t)的持续周期为t∈[a,b]，将信号持续期[a,b]按单位等分间隔h=1进行等分，则式(5)中m=(b-a)h=b-a，则s(t)分数阶微分的差值表达式可为

(11)

在处理数字图像时，计算机或者数字滤波器处理的是数字量，图像灰度f(x,y)之间的变化是有限的，并且发生的最短距离为相邻2像素之间.因此二维数字图像在x和y轴方向上的持续时间只能以像素为单位进行度量，f(x,y)的最小等分间隔只能是h=1.则针对数字图像，本定义f(x,y)在x和y坐标轴正方向上分数阶偏微分差分的近似表达式为

(12)

(13)

从式(12)和式(13)可以看出每1项的系数值都不相同，各项系数之和不等于0.这是与整数阶微分最显著的区别，系数的通项式为

(14)

其中，Γ(·)为Gamma函数.根据整数阶的梯度定义，重新定义分数阶梯度：

(15)

则分数阶梯度向量的模值为

(16)

在数值运算时，为简化运算，近似取分数阶微分表达式(12)和式(13)的前M项，构造M×M分数阶微分模板，X正方向和Y正方向的模板如图1所示：

︙︙︙︙︙000…01-α(-α)(-α+1)2…Γ(-α+m-1)(m-1)!Γ(-α)000…0︙︙︙︙︙

…010……0-α0……0(-α)(-α+1)20……︙︙︙……0Γ(-α+m-1)(m-1)!Γ(-α)0…

Fig. 1 Differential mask in X axis and Y axis positive direction
图1 X轴和Y轴正方向上分数阶微分掩模

2.1.2 新的拟合项

RSF模型在分割弱纹理、弱边缘图像时，演化曲线易陷入局部最优原因有2个：1)仅仅利用图像的局部信息；2)水平集曲线在演化过程中运动到图像的弱边缘处或纹理丰富区域时，由于这些区域的灰度变化不大，造成演化曲线的驱动力小，容易陷入局部最小值.为使演化曲线运动到目标轮廓，则对于曲线的初始位置有着严格的要求.基于G-L的分数阶梯度可以增强弱边缘及纹理丰富区域的梯度信息,将G-L分数阶梯度信息融合到能量方程中，作为曲线拟合的另一种驱动力，演化曲线在局部灰度拟合项和全局的分数阶微分梯度拟合共同驱动下，运动到目标轮廓.结合G-L分数阶梯度和CV模型特点，构建新的能量方程：

EFG(m1,m2,C)=

(17)

EFG(m1,m2,φ)=

(18)

其中，m1和m2计算为

(19)

其中，Hε(φ)和δε(φ)分别是海氏(Heaviside)函数和狄拉克(Dirac)函数的正则化形式.将这个能量方程融合到RSF模型中，则总的能量方程为

(20)

求能量方程式(20)的最小值可以通过求解能量泛函对应的Euler-Lagrange方程来实现.采用梯度下降法得到曲线的水平集演化方程:

(21)

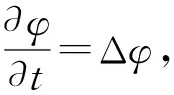
φn+1=φn+Δt×Δφ.

(22)

2.2 自适应分数阶微分的推导

2.2.1 分数阶微分对信号的作用

对一个任意平方可积的能量信号I(x)∈2，由信号处理的基本理论可知其Fourier变换为

x.

(23)

假设信号I(x)的n阶导数为I(n)(x)(n∈)，根据Fourier变换的性质可以得到：

(24)

由整数阶推广到分数阶，I(x)的α分数阶导数为I(α)(x)(α∈+)，同样根据分数阶Fourier变换为

(25)

其中:

(26)

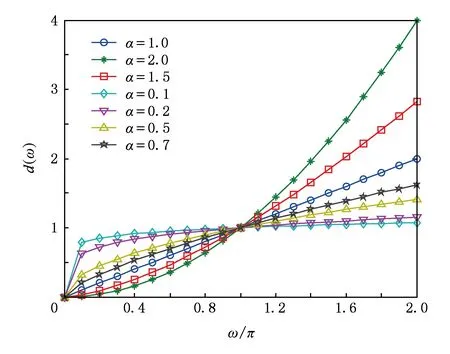
Fig. 2 The amplitude-frequency curve of fractional differentiator图2 分数阶微分算子的幅频特性曲线

根据式(25)和式(26)绘制分数阶微积分的幅频特性曲线，如图2所示.从图2可以看出在0<ω<1的低频信号段，分数阶微分对信号的衰减程度低于整数阶微分，而在ω>1的高频信号段，分数阶微分对信号的增强程度低于整数阶微分.因此得出以下结论：分数阶微分在增强信号的高频部分的同时能非线性地保留信号的中低频成分.在数字图像中，图像的弱边缘以及纹理丰富的区域属于低频信息，图像的噪声属于高频信息，在整数阶微分中弱边缘以及纹理信息往往会被较大地衰减，而噪声信号被极大地增强.但是运用分数阶微分能够很好地克服该缺陷，噪声信号不会被极大地增强，弱边缘以及纹理信息会被非线性地保留，因此将分数阶微分运用到数字图像处理中，不仅有利于保留弱边缘以及纹理信息，还具有一定的抗噪性.总之,根据图像处理关注的目标不同,我们选用不同范围的阶次.本文需要保留纹理和弱边缘，因为从幅频曲线图中可以得出，不同的α值对信号低频部分的保留效果不一样，当0<α<1时，信号低频部分保留效果较好，信号的高频部分相比于整数阶得到了抑制，因此本文α的取值建议在0～1之间.

2.2.2 相关特性的选择

由2.1节可知，RSF模型在分割存在弱纹理、弱边缘特征的图像时，优化容易陷入局部最优.因此将分数阶梯度融合到RSF模型中，分数阶梯度增强的程度直接影响最终的分割结果.结合分数阶幅频特性曲线，如图2所示，分数阶阶次越小，与整数阶相比增强的程度越大，所以在低频区域应选择较小的分数阶增强，而在高频区域不需要增强，对噪声还需抑制，故选择较大的分数阶阶次.所以在选择分数阶阶次时，应根据图像的相关特征选取最佳的阶次，而不是整幅图像都选用相同的阶次.由于图像的整数阶(1阶)梯度反映了像素值的突变，整数阶梯度对图像的纹理比较敏感.所以整数阶梯度的变化可以用来判断图像中纹理信息的情况，图像的信息熵S同样也可以反映图像的纹理特性，在图像的平滑区域，S较小；而在图像的纹理区域，信息熵S较大.因此可以根据整数阶梯度和图像信息熵来构造自适应分数阶函数，通过该函数实现分数阶阶次的自动计算.

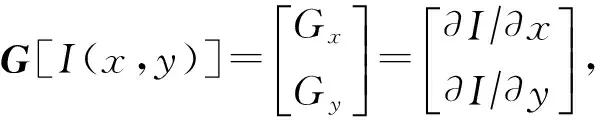
(27)

定义2. 信息熵是一种信息量的度量，反应图像纹理信息的丰富程度.因此，在图像的边缘和纹理区域具有更大的图像信息熵，其定义为

(28)

其中,S信息熵值，i,j为像素坐标，Iij为灰度值，ω为模板，Pij在模板内相同灰度值的概率.

在图像的分割过程中，分数阶阶次不仅和图像的梯度模值有关，并且受到图像信息熵的影响.通过分析定义1和定义2可以得出，图像梯度模值和信息熵越大，该区域为边缘或纹理的可能性越大，那么对这些区域进行分数阶梯度增强的程度应该较大；反之，该区域为边缘或纹理的可能性越小.那么对这些区域进行分数阶梯度增强的程度应该较小.

2.2.3 构建分数阶阶次自适应数学模型

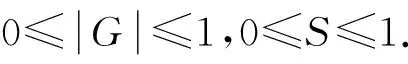
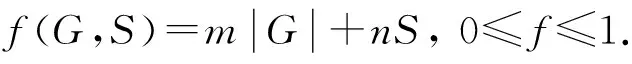
(29)

其中，m,n为权值，且m+n=1.

如图2所示，由分数阶幅频特性曲线可知，当阶次在区间[0，1]，随着分数阶阶次的降低，与整数阶相比增强的程度越强，反之越弱.在本文阶次选择过程中，当f值较小时，认为是平滑区域，从而增强的程度应该减小，分数阶阶次应选择较大的值；反之选择较小的值.本文阶次的研究范围在0～1之间，则选择2个极限值为0和1进行讨论.具体阶次的选择分2种情况确定：1)判断某个像素点的梯度值是否小于设定的阈值，如果梯度值小于阈值，则认为该点与相邻像素点之间的灰度差为0，在这个像素点上不存在像素突变，可以得出该点所处的位置不是边界，有可能是平滑区域或者弱纹理区域，因此阶次根据信息熵值确定，式(29)中的m=0，n=1；2)当某个像素点的梯度值大于阈值，在该点存在像素突变，认为该点所处的位置是边界，因此阶次根据梯度模值和信息熵共同确定，式(29)中的m,n均取0.5.为保证阶次的选择在0～1之间，本文选择sigmod函数为原型函数.由于该函数是一个良好的阈值函数，光滑、连续、严格单调，常用于神经网络作为激发函数，对目标进行分类.分数阶阶次的选择类似于对阶次进行分类选择，以sigmod函数为原型，构造分数阶阶次与图像梯度模值和熵值按照一定规律自适应变化的函数，定义如下：

(30)

其中,k和b为待定的系数.当f=1时，该区域为边缘或纹理区域的可能性越大，是需要增强的区域，则α=0表示增强极限最大，直接取该点的灰度值；f=0时，该区域为边缘或纹理区域的可能性越小，是不需要增强的区域，则α=1表示不增强，选择整数1阶梯度值.即将f=1,α=0和f=0,α=1代入式(30)构成如下方程，并计算得到k和b的值.

将k和b的值代入自适应函数，则：

(31)

式(31)即为自适应分数阶阶次模型.

计算分数阶阶次的流程图如图3所示:

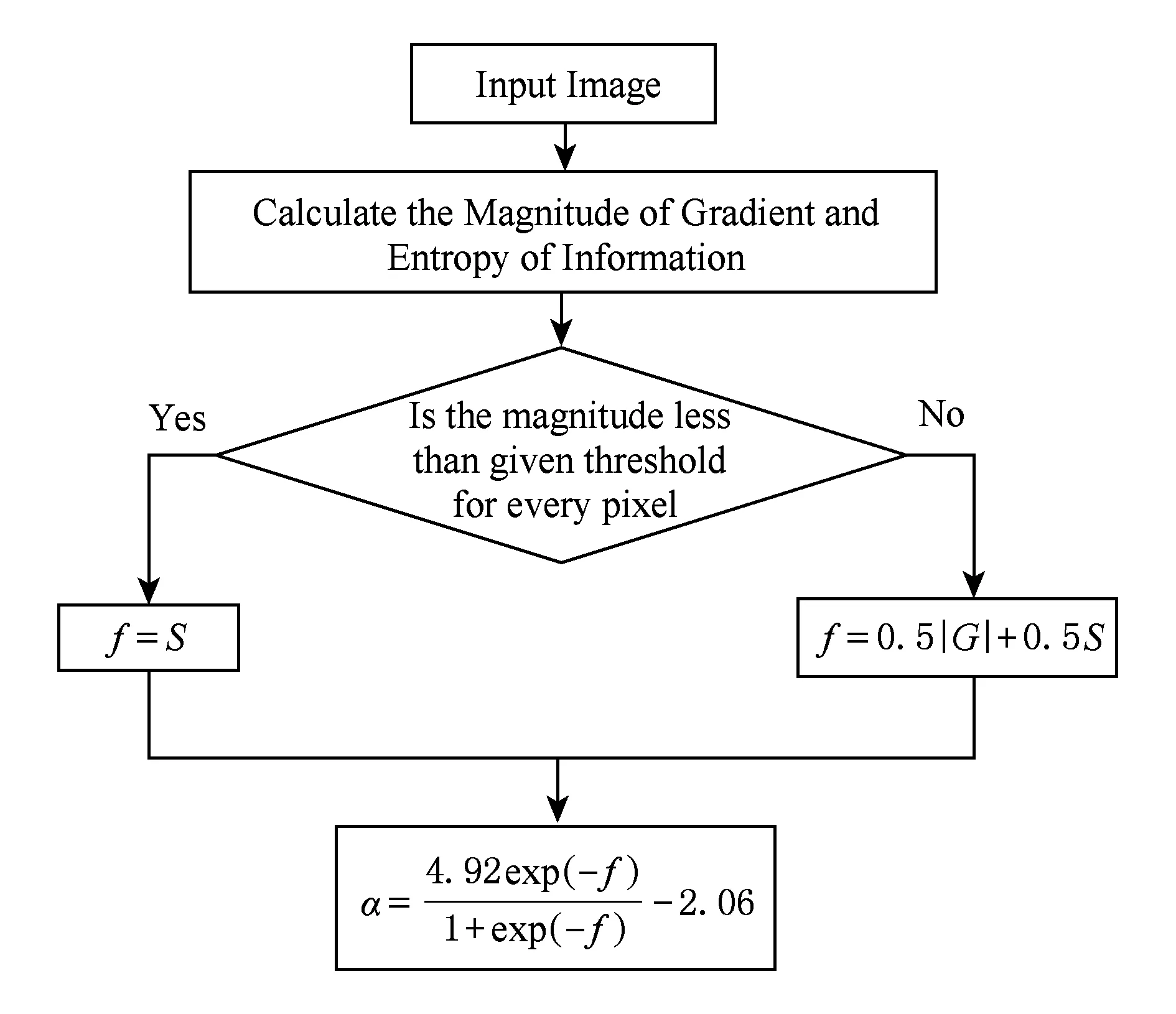
Fig. 3 Flow chart of adaptive fractional order图3 自适应分数阶阶次的流程图

2.3 基于双边滤波的拟合项

由于在RSF的拟合项中(式(1))使用了高斯核函数，即该算法利用了局部信息，故能够分割灰度不均匀的图像.然而高斯核函数的副作用是对图像进行了平滑，使得弱边缘更加模糊.由于仅仅考虑了各像素点位置之间的关系，忽略了各灰度值之间的差异性，从而使图像的边界模糊，因此曲线在演化过程中无法精确定位，尤其是弱边缘、弱纹理的区域部分，曲线演化易陷入局部最优，无法得到正确的分割结果.为更好地分割具有弱边缘、弱纹理特征的图像，应选择具有高斯核函数的功能，又能够很好地保持边缘的核函数，而双边滤波正好具有这种性能.

Fig. 4 Original image S图4 原图S

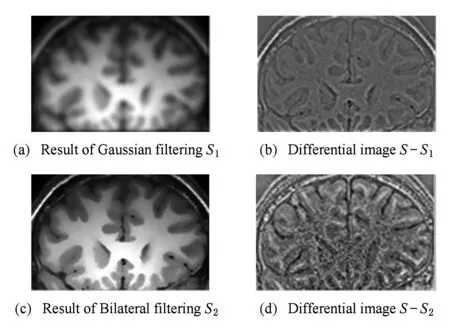
Fig. 5 Effect comparison of two kind of filters图5 2种滤波结果对比

为了验证双边滤波的去噪保边性能，输入如图4所示的脑部MRI图像，该图像中的灰度分布不均匀.用高斯滤波和双边滤波进行实验对比，实验结果如图5所示，从图5可以看出，高斯滤波的结果模糊，边界弱化，原图S和高斯滤波后结果S1差值图像信息丰富，可以看出明显的轮廓结构；而双边滤波的结果清晰，边界明显，原图S和双边滤波后的结果S2的差值图像信息模糊，看不出明显的轮廓结构.所以双边滤波相比于高斯滤波能够保持更多的边界信息.

受此启发，本文用双边滤波函数代替高斯核函数，双边滤波的权重系数不仅考虑各像素点位置之间的关系，同时还考虑了各像素值之间的差异性.在图像的平滑区域，灰度值之间的差异不大，双边滤波的权重系数所起的效果等同于高斯核函数；在弱边缘、弱纹理区域，灰度值之间存在差异，双边滤波的权重系数起到了边缘保持的作用.从而增强了RSF模型对具有弱边缘、弱纹理特征图像的分割能力.其具体定义为

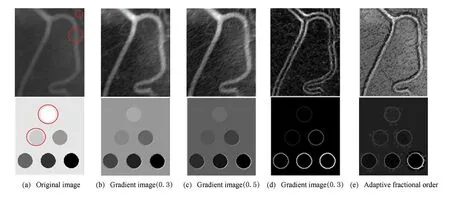
Fig. 6 Input image and enhance results of different methods图6 输入原图和不同方法增强后的结果图

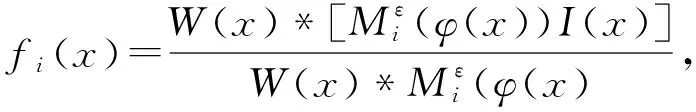
(32)

其中，i=1,2.

2.4 算法步骤

算法1. 图像分割算法.

Step1. 设置参数μ,ν,λ1,λ2,β1,β2以及初始化水平集函数φ0；

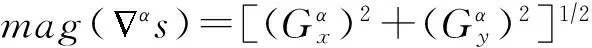
Step3. 根据公式

计算f1,f2，再计算曲线内外的平均分数阶梯度值

Step4. 固定f1,f2，m1，m2,根据式(21)和式(22)更新水平集函数；

Step5. 判断水平集函数是否达到稳定，若达到稳定状态则输出最终结果，否则返回Step3.

3 实验结果与分析

实验中所采用的计算机环境为：实验机器配置Intel Core i3-2130 CPU、内存4 GB、操作系统为64位Windows 7.0，程序采用R2013a版Matlab，实验图像选用人工合成和真实图像.本文从自适应分数阶梯度增强、分割性能验证、自适应分数阶的最佳阶次分析3个方面进行实验，并对实验结果进行分析和讨论.

3.1 自适应分数阶梯度增强

为验证自适应分数阶阶次的RSF模型能更好地增强弱边缘、弱纹理区域的梯度，本次实验选取了2幅具有弱边缘、弱纹理特征的输入图，如图6(a).分别计算分数阶0.3阶、分数阶0.5阶、整数1阶、自适应分数阶梯度模值图，实验结果如图6所示.图6(a)为输入图，图6(b)～6(e)分别为0.3阶、0.5阶、整数1阶以及自适应阶次的增强结果图，图6(a)中圆圈区域的目标与背景的灰度接近.从增强结果来看，分数阶的阶次取值为0.3和0.5时都可以得到边缘增强的效果.但是，若整幅图像均采用相同的阶次，则整幅图像增强的幅度相同，即没有突出增强圆圈区域内的弱边缘，而其他区域出现了过增强；整数1阶没有起到增强的作用，有较多的弱边缘不清晰.图6(e)自适应分数阶之所以能够更好地凸显弱纹理和边界特征，是因为该方法根据图像的整数阶梯度以及信息熵自适应计算分数阶阶次，并且在每个像素点都取到其最佳的阶次，所以能够更有效地突出增强弱纹理、弱边界区域，而平滑区域不增强，从而避免了其他一些无需增强区域的过增强的副作用.

3.2 分割性能的验证

为验证本文算法对具有弱纹理、弱边缘特征的图像具有更好的分割性能，选取了4幅医学图像(如图7(a)所示的4幅图像，并分别编号为Ⅰ，Ⅱ，Ⅲ，Ⅳ)，这4幅图像均具有灰度分布不均匀、弱边缘、弱纹理特征.将本文算法与RSF模型、文献[6]、文献[16]以及人工选取最佳阶次进行对比，并用最终分割结果图、演化迭代次数来评定各种算法的分割性能.实验中各模型的相关参数均取各自文献中选用的参数，本文算法参数根据多次实验结果，设置为

Ⅰ：Δt=0.1,λ1=β1=β2=1,λ2=2,μ=1,σ=3,ν=0.004×255×255,分数阶微分模板大小是3×3；

Ⅱ：λ1=2,λ2=1，其他同I的参数；

Ⅲ：参数与Ⅱ的参数相同；

Ⅳ：λ1=λ2=1，ν=0.002×255×255，其他与Ⅰ的参数相同.

实验结果如图7所示，图7(a)为输入图像，图7(a)中的方框表示选择的曲线初始位置，图7(b)～(d)以及图7(f)分别为RSF模型、文献[6]、文献[16]和本文方法的分割结果，图7(e)为人工选取最佳阶次时的分割结果；第1～4行的最佳阶次分别为0.2,0.5，0.4，0.5.图7(b)～(f)的曲线表示分割出的目标轮廓.从图7可以看出RSF模型和文献[16]均陷入了局部最优，不能正确分割出结果；文献[6]出现了过分割的现象；本文的分割方法自适应选择阶次和人工选取最佳阶次均得到理想的分割结果.

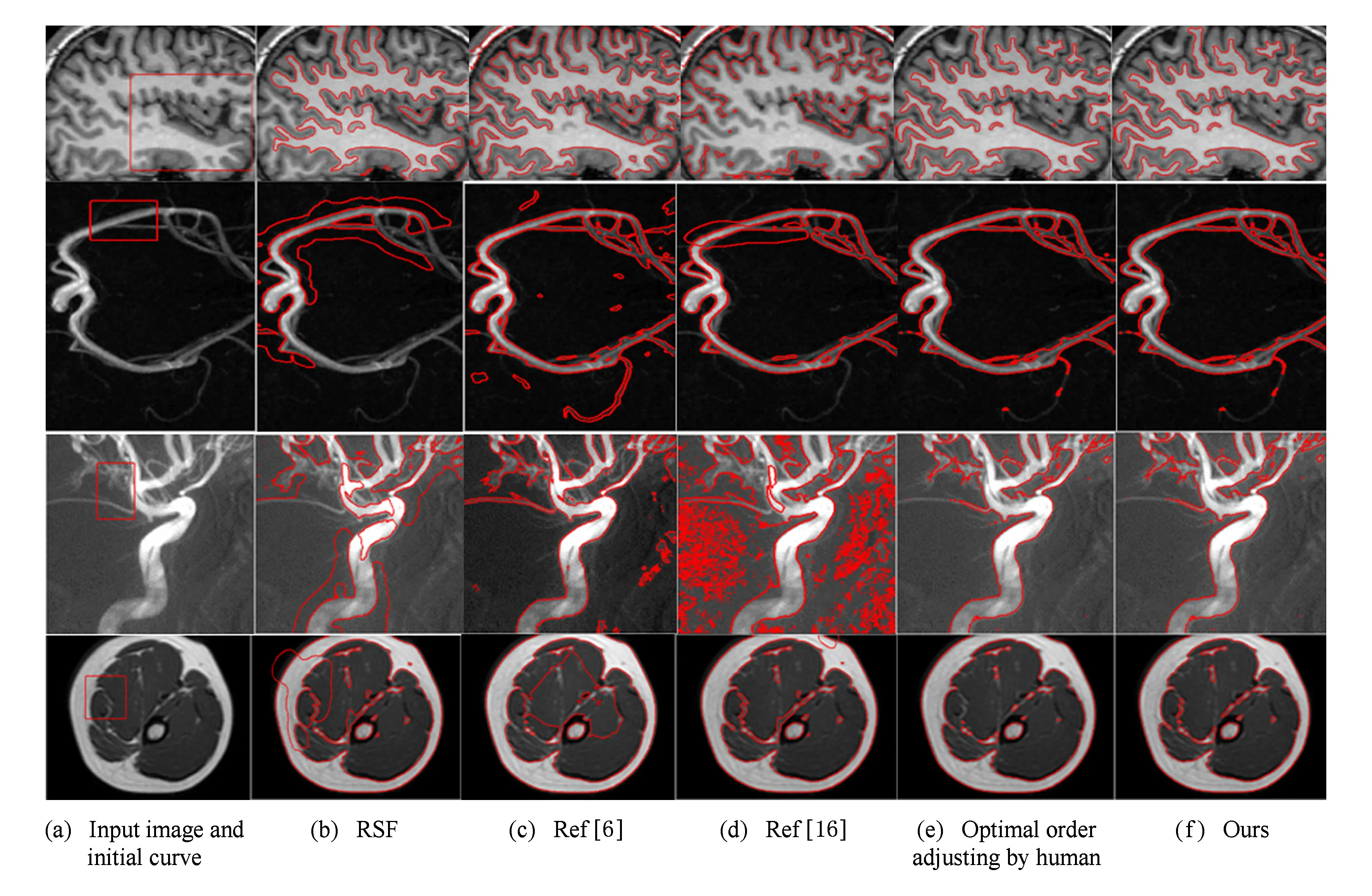
Fig. 7 Input image and segmentation results of different methods图7 输入图和不同方法分割结果

Fig. 8 Iterations of different segmentation models图8 各分割模型的迭代次数比较

此外为了比较该4种方法的分割效率，本文通过比较4种算法的迭代次数，结果如图8所示，本文算法的迭代速度比RSF模型和文献[16]有较大的提升，这是因为本文算法在保留原始RSF模型优点的同时，还融入了新的分数阶拟合项，增加了演化曲线的驱动力，从而加速了演化过程，减少了迭代次数.与文献[6]相比，本文算法在迭代次数上没有优势，是因为文献[6]通过局部聚类准则对图片进行了灰度不均校正，得到类似于原图一个灰度均匀的偏差图，所以能较快地得到分割结果，但容易出现过分割.本文算法在局部拟合项中融合了双边滤波，这是一个非线性滤波，因此迭代速度有所降低.但双边滤波具有较好的保边性能，能防止边界弱化，因此比文献[6]有较高的分割精度.故本文提出的方法在效率稍有降低的前提下对分割精度有较大的提升.

Fig. 9 Segmentation results of four different initial curves by using our method图9 本文算法在4种不同初始位置下的分割结果

3.3 自适应分数阶的最佳阶次分析

本次实验的目的是为了验证自适应分数阶的数学模型正确性，将本文自适应计算分数阶阶次的方法与人工调节阶次的方法进行比较(其他步骤相同，仅仅阶次的选择方法不同)，选取具有灰度不均匀、弱边缘、弱纹理特征的医学图片，如图9所示.为进一步对分割结果进行评价，本文定义了正确分割率(correct segmentation rate,CSR)，并用正确分割率对分割结果进行定量分析.

(33)

其中，φ1是人工标定目标轮廓的水平集，φ2是演化后最终的水平集，N(φ1∩φ2)是两水平集相同符号的像素点个数，N(φ1),N(φ2)是水平集的像素点个数.从式(33)可以看出，CSR的值越大分割越准确.

图9(a)表示输入图像及不同的初始位置，图9(b)表示了本文算法在4种不同初始位置下的分割结果，从图9可以看出本文的分割方法在不同初始位置时，都得到了正确的分割结果，按照式(33)计算本文算法的正确率均达到了100%.同时还绘制了在图9中4种不同位置(从左至右)下不同的分数阶阶次α与正确分割率的曲线图，如图10所示.从图10可以得出，位置3只有当阶次为0.7时分割正确率达到100%，而在其他3种位置时分割正确率达到100%时的阶次均在0.75～0.85的区间段内.所以，在上述4种位置下人工选择的分数阶阶次在0.7～0.85之间均可以得到正确的分割结果,但是人工调阶这个过程非常费时费力的.而自适应选择分数阶阶次同样完成了分割目的，却避免了寻找最佳阶次的过程.

Fig. 10 Curves between order and segmentation accuracy图10 阶次α与正确分割率的关系(4种初始位置)

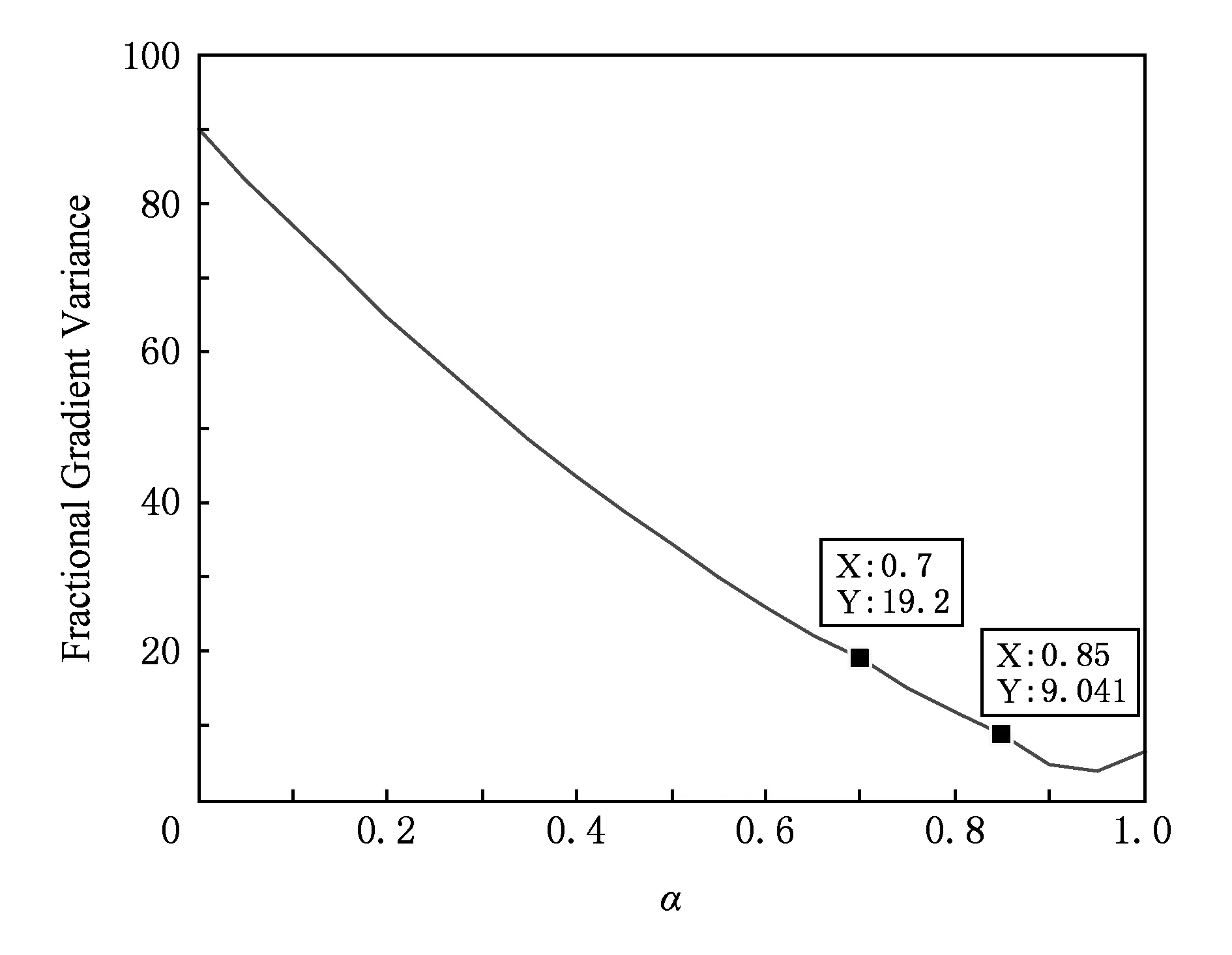
Fig.11 Curves between order and gradient variance图11 阶次α与分数阶梯度方差的关系

为了进一步确定自适应选择阶次和人工选择最佳阶次之间的联系，通过统计计算发现分数阶梯度方差与分数阶阶次的关系是一一对应，于是绘制了分数阶阶次与分数阶梯度方差之间的曲线图，在0～1区间内，随着阶次的增加，分数阶梯度方差将减小，如图11所示.从图10的曲线图已经得出，在4种不同的初始位置下，能正确完成分割任务的阶次在0.7～0.85之间、在图11中，上述区间内的分数阶梯度方差由19.2降到9.041.由于自适应算法在各点计算的阶次不同，所以无法计算具体的阶次.但是可以计算出图像的分数阶梯度方差是18.66，并接近19.2,从而可以推断出自适应算法的综合分数阶阶次接近0.7.本文算法之所以有这样的分割结果是因为结合了整数阶梯度模值和图像的信息熵，通过这2个参数判断图像的边界和纹理结构，并且构造分数阶阶次的自适应函数，根据纹理和边界的强弱自适应计算最佳阶次，节省了寻找最佳阶次的工作量，最终得到正确的分割结果.

4 结 论

将G-L分数阶微分的全局梯度信息融合到RSF模型中，并用双边滤波函数替代局部拟合项中的高斯核函数，解决了RSF模型在分割弱边缘、弱纹理图像时易陷入局部最优的问题.一方面，将全局G-L分数阶梯度融合到RSF模型中，即在RSF模型中增加全局的分数阶梯度拟合项，提高演化曲线的驱动力，避免演化曲线在图像的弱边缘及纹理丰富区域陷入局部最优；另一方面在局部拟合项中使用双边滤波函数，既考虑了像素空间位置的因素，又考虑了灰度值之间的差异性，避免边界弱化，从而提高了边界定位能力.此外基于图像梯度模值和信息熵，构造了自适应分数阶阶次的数学模型，自动自适应计算整幅图像中各个区域的阶次.理论分析和实验结果均表明改进后的算法能够更好地增强图像弱边界、弱纹理区域的梯度，能够根据图像的特征自适应计算分数阶的最佳阶次，省去了费时费力地寻找最佳阶次的工作，提高了图像分割的效率，图像的分割精度也得到提高.另外本文通过计算自适应分数阶梯度值的方差，绘制了分数阶阶次与分数阶梯度值方差的曲线图，验证了分数阶自适应模型的正确性.不足之处是自适应数学模型的建立仅考虑了图像的梯度模值和信息熵，所以该模型并不是最优的模型.今后的研究工作将进一步优化自适应数学模型，提高计算速度，进而提高分割效率.

[1]Jiang Guiping, Qin Wenjian, Zhou Shoujun, et al. State-of-the-art in medical image segmentation[J]. Chinese Journal of Computers, 2015, 38(6): 1222-1242 (in Chinese)(江贵平, 秦文健, 周寿军, 等. 医学图像分割及其发展现状[J]. 计算机学报, 2015, 38(6): 1222-1242)

[2]Xu Xinzheng, Ding Shifei, Shi Zhongzhi, et al. New theories and methods of image segmentation[J]. Acta Electronica Sinica, 2010, 38(2): 76-82 (in Chinese)(许新征, 丁世飞, 史忠植, 等. 图像分割的新理论和新方法[J]. 电子学报, 2010, 38(2): 76-82)

[3]Li Chunming, Kao C-Y, Gore J C, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Trans on Image Processing, 2008, 17(10): 1940-1949

[4]Wang Bin, Gao Xinbo, Tao Dacheng, et al. A nonlinear adaptive level set for image segmentation[J]. IEEE Trans on Cybernetics, 2014, 44(3): 418-428

[5]Wang Bin, Li Jie, Gao Xinbo. An edge- and region-based level set method with shape priors for image segmentation[J]. Chinese Journal of Computers, 2012, 35(5): 1067-1072 (in Chinese)(王斌, 李洁, 高新波. 一种基于边缘与区域信息的先验水平集图像分割方法[J]. 计算机学报, 2012, 35(5): 1067-1072)

[6]Li Chunming, Huang Rui, Ding Zhaohua, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE Trans on Image Processing, 2011, 20(7): 2007-2016

[7]Bai Xuefei, Wang Wenjian, Liang Jiye. An active contour model based on region saliency for image segmentation[J]. Journal of Computer Research and Development, 2012, 49(2): 2686-2695 (in Chinese)(白雪飞, 王文剑, 梁吉业. 基于区域显著性的活动轮廓分割模型[J]. 计算机研究与发展, 2012, 49(2): 2686-2695)

[8]Unde A S, Premprakash V A, Sankaran P. A novel edge detection approach on active contour for tumor segmentation[C] //Proc of IEEE SCES-2012. Piscataway, NJ: IEEE, 2012: 1-6

[9]Hai Min, Wang Xiaofeng. A novel level set model based on multi-scale local structure operation for texture image segmentation[J]. Journal of Information and Computational Science, 2015, 12(1): 9-20

[10]Pu Yifei, Wang Weixin. Fractional differential masks of digital image and their numerical implementation algorithms[J]. Acta Electronica Sinica, 2007, 33(11): 1128-1135 (in Chinese)(蒲亦非, 王卫星. 数字图像的分数阶微分掩模及其数值运算规则[J]. 自动化学报, 2007, 33(11): 1128-1135)

[11]Gao Chaobang, Zhou Jiliu. Image enhancement based on quaternion fractional directional differentiation[J]. Acta Electronica Sinica, 2011, 37(2): 150-159 (in Chinese) (高朝邦, 周激流. 基于四元数分数阶方向微分的图像增强[J]. 自动化学报, 2011, 37(2): 150-159)

[12]Yang Zhuzhong, Zhou Jiliu, Lang Fangnian. Noise detection and image de-noising based on fractional calculus[J]. Journal of Image and Graphics, 2014, 19(10): 1418-1429 (in Chinese)(杨柱中, 周激流, 郎方年. 基于分数阶微积分的噪声检测和图像去噪[J]. 中国图象图形学报, 2014, 19(10): 1418-1429)

[13]Pu Yifen, Siarry P, Zhou Jiliu, et al. A fractional partial differential equation based multiscale denoising model for texture image[J]. Mathematical Methods in the Applied Sciences, 2014, 37(12): 1784-1806

[14]Wang Chengliang, Lan Libin, Zhou Shangbo. Adaptive fractional differentional and its application to image texture enhancement[J]. Jouranl of Chongqing University, 2011, 34(2): 32-37 (in Chinese)(汪成亮, 兰利彬, 周尚波. 自适应分数阶微分在图像纹理增强中的应用[J]. 重庆大学学报, 2011, 34(2): 32-37)

[15]Hu Fuyuan, Si Shaohui, Zhang Yanning, et al. Multi-bilateral filtering algorithm based on adaptive fractional order differentiation[J]. Journal of Image and Graphics, 2013, 18(10): 1237-1246 (in Chinese)(胡伏原, 姒绍辉, 张艳宁, 等. 自适应分数阶微分的复合双边滤波算法[J]. 中国图象图形学报, 2013, 18(10): 1237-1246)

[16]Ren Z. Adaptive active contour model driven by fractional order fitting energy[J]. Signal Processing, 2015, 117: 138-150

[17]Zhang Jun, Wei Zhihun, Xiao Liang. Adaptive fractional-order multi-scale method for image denoising[J]. Journal of Mathematical Imaging and Vision, 2012, 43(1): 39-49

[18]Tian Dan, Zhang Xiaodan, Fan Linan. A fractional-order level set model for image segmentation[J]. International Journal of Digital Content Technology and Its Applications, 2013, 7(2): 622-630

[19]Chan T F, Vese L. Active contours without edges[J]. IEEE Trans on Image Processing, 2001, 10(2): 266-277

[20]Cafagna D. Fractional calculus: A mathematical tool from the past for present engineers[J]. IEEE Industrial Electronics Magazine, 2007, 1(2): 35-40

[21]Tomasi C, Manduchi R. Bilateral filtering for gray and color images[C] //Proc of the 9th Int Conf on Computer Vision. Piscataway, NJ: IEEE, 1998: 839-846

A New Active Contour Model Based on Adaptive Fractional Order

Zhang Guimei1, Xu Jiyuan1, and Liu Jianxin2

1(Key Laboratory of Jiangxi Province for Image Processing and Pattern Recognition (Nanchang Hangkong University), Nanchang 330063)2(School of Mechanical Engineering, Xihua University, Chengdu 610039)

Region scalable fitting (RSF) active contour model has limitation in segmenting image with weak texture and weak edge, troubled by inclining to local minimum and slow evolution speed. Aiming at the problem, this paper proposes a new active contour model with fractional order derivative operator capable of adjusting degree adaptively. Firstly, the global Grünwald -Letnikov (G-L) fractional gradient is integrated with the RSF model, which can strengthen the gradient of regions with intensity inhomogeneity and weak texture. As a result, both the robustness to initial location of evolution curve and efficiency of image segmentation are improved. Secondly, the Gaussian kernel function in local fitting term is replaced by bilateral filtering, and the blurred boundary caused by Gaussian kernel function in the process of curve evolution can be tackled. Lastly, an adaptive fractional order mathematical model is constructed based on the gradient magnitude and information entropy of image, therefore the optimal fractional degree is adjusted adaptively. Theoretical analysis and experimental results show that the proposed algorithm is capable of segmenting images with intensity inhomogeneity and weak texture. And the optimal degree of fractional order derivative operator can be calculated adaptively. Furthermore, the presented method is capable of avoiding falling into local optimum, thus the efficiency of image segmentation can be improved.

Grünwald-Letnikov fractional order; adaptive fractional order; RSF model; active contour model; image segmentation

Zhang Guimei, born in 1970. PhD and professor. Senior member of CCF. Her main research interests include computer vision, image processing and pattern recognition, etc.

Xu Jiyuan, born in 1989. Master. His main research interests include image processing and machine learning (872410955@qq.com).

Liu Jianxin, born in 1969. PhD and professor. His main research interests include computer vision, image processing and machine learning, etc.

2016-04-26；

2016-10-10

国家自然科学基金项目(61462065)；江西省自然科学基金项目(20151BAB207036)；江西省科技支撑计划基金项目(20161BBF60091) This work is supported by the National Natural Science Foundation of China (61462065), the Natural Science Foundation of Jiangxi Province of China (20151BAB207036), and the Key Technology Research and Development Program of Jiangxi Province of China (20161BBF60091).

刘建新(jamson_liu@163. com)

TP391.41