局部Hilbert边际能量谱在滚动轴承故障诊断中的应用

杨恭勇，周小龙，李家飞，梁秀霞

(1.东北电力大学 工程训练教学中心 吉林 吉林 132012；2.河南信宇石油机械制造股份有限公司 河南 濮阳 457001)



局部Hilbert边际能量谱在滚动轴承故障诊断中的应用

杨恭勇1，周小龙1，李家飞2，梁秀霞2

(1.东北电力大学 工程训练教学中心 吉林 吉林 132012；2.河南信宇石油机械制造股份有限公司 河南 濮阳 457001)

针对滚动轴承振动信号非线性的特点，提出一种基于局部希尔伯特边际能量谱和马氏距离判别法相结合的故障诊断方法。首先，采用镜像延拓方法抑制经验模态方法将待分析信号分解成多阶固有模态函数和的形式，并根据相关性判别算法选取含有主要故障信息的IMF分量；其次，利用局部Hilbert边际能量谱提取故障信号能量特征参数；最后，利用马氏距离算法对滚动轴承的工作状态进行判别。通过相关试验证明了此方法的有效性，具有一定的工程应用价值。

经验模态分解；局部Hilbert边际能量谱；马氏距离；滚动轴承；故障诊断

滚动轴承为各种机械设备中不可缺少的用于支撑转轴的重要部件[1]。对于存在故障的滚动轴承故障信号而言，其常常具有非平稳的时变特性[2]。对于此类信号，常采用时频分析方法对其进行故障诊断研究。在众多时频分析方法中，小波变换的应用最为广泛。然而该方法具有自身的局限性[3]，在分析非平稳信号时往往难以得到满意的效果。希尔伯特-黄变换(Hilbert-Huang Transform，HHT)[4]方法是近年来得到研究人员广泛关注的一种新的信号处理和分析方法，HHT自身的自适应性使得该方法在旋转机械故障诊断领域得到广泛应用[5-6]，但该HHT方法的端点效应和虚假模态等问题严重影响了此方法在该领域的发展。

基于上述分析，并结合滚动轴承振动信号的特性，本文提出一种基于局部Hilbert边际能量谱和马氏距离判别算法相结合的故障诊断方法。并通过试验研究，验证了所提方法的有效性。

1 改进的HHT

HHT方法在处理旋转机械故障诊断问题方面的不足主要表现为：端点效应[7]和虚假固有模态函数(I)IMF分量[8]等问题。这些问题严重限制了HHT方法诊断的准确性。在此，采用边界局部特征尺度延拓法[9]与相关性分析法相结合的改进HHT方法解决上述问题。

1.1 端点优化对称延拓算法

EMD方法是根据信号的局部特性将其分解成多阶表征信号特性的IMF，据此所采用的端点优化对称延拓算法的步骤如下：

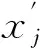
(1)

(2)以b、a为中心将所延拓的信号序列侧进行对称延拓以保证信号序列的结构不变性，则经对称延拓后的信号序列h：

(2)

式中：i=0,1,…,n-1。并采用三次样条插值法获得此信号序列的包络线S。当S与hi偏差最小时的信号序列所延拓的端点为最优延拓点，此延拓点可由号hi与其相应包络Si的偏差评价函数来确定：

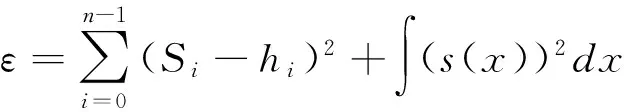
(3)

在∂ε/∂b=0且∂ε/∂a=0时，求出b、a的值。

由EMD算法可知，EMD出现端点效应现象的主要原因是在信号端点处未做约束，而此方法正是根据信号端点处的自身特性来解决此问题，所以此方法能够有效解决EMD分解过程中所存在的端点效应问题。

1.2 虚假IMF判别算法

由于EMD算法具有正交性，所以经EMD分解得到的各IMF分量与原信号间应具有较好的相关性[10]，由此，可以求取各IMF分量同所分解信号间的相关系数来选取对信号信息敏感的IMF分量。从而有效避免虚假模态分量问题对于分析准确性的影响。

设信号x(t)经改进EMD分解后得到n阶IMF分量，即c1(t)，c2(t)，…，cn(t)，则其相关系数ρi为

(4)

分别计算各阶IMF分量同原始信号间的相关系数，并由信号自身特性选取门限阈值判别出包含主要故障信息的IMF。

2 基于局部Hilbert边际能量谱的特征能量法

对于滚动轴承而言，当它自身出现故障时，会使滚动轴承系统在固有频率段的信号能量发生变化[11]，由之前分析可知，经HHT方法所获得的信号的Hilbert谱是信号能量的一种完整的时-频分布，这为以Hilbert谱为基础对滚动轴承进行故障诊断提供了理论依据。

EMD分解出的每一阶IMF分量的频率和能量(幅值)都是时间的函数，所以，信号的Hilbert谱H(ω,t)准确地描述了所分析信号的幅值同其时间和频率的变化及分布情况。若将x(t)2作为信号的能量密度，经HHT分析后，信号的Hilbert谱H2(ω,t)同样具有此物理意义，故特将H2(ω,t)定义为信号的Hilbert能量谱。它在时-频区间上表述了信号的能量变化情况，略去信号残差后，不同工况下滚动轴承的振动信号在HHT分析前后应满足能量守恒，则有：

(5)

由此可定义E(ω)为Hilbert边际能量谱，即：

(6)

由式(6)可知，信号能量随频率的变换情况可在E(ω)中得到准确反映。而当滚动轴承出现故障时，其固有频率段的能量会有有所增大，所以可选择对敏感IMF分量进行Hilbert分析，求出表征信号主要状态特性的局部Hilbert谱H′(ω,t)：

(7)

将E′(ω)定义为信号x(t)的边际能量谱，它反应了在固有频率段的能量随频率的变化情况，所以可进一步定义在固有频率区间ω1～ω2的能量为特征向量：

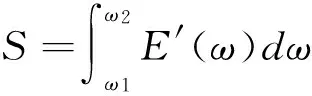
(8)

式中：ω1～ω2为固有频率段，S为相应工作状态下滚动轴承振动信号的能量。因此，可将S作为滚动轴承故障的特征值进行后续诊断研究。

3 基于M距离的滚动轴承故障诊断

马氏距离是多元数理统计理论中常用的判别方法之一，由于该方法不受量纲的影响，同时算法简单，计算速度快，因此，非常适用于小样本问题的分析[12]。

选择之前计算的滚动轴承各不同状态下在固有频率段的能量S作为训练样本，进行马氏距离分析，具体步骤如下：

(1) 按一定的采样频率fs对不同工况下滚动轴承的故障信号进行采样，在此，滚动轴承的共有正常状态、内圈故障状态和外圈故障状态等三种工况，每种工况的采用次数为30次；

(2) 对每个所采集到的振动信号进行改进EMD分解，获得其IMF分量；

(3) 采用基于相关性的虚假IMF判别算法，选取敏感IMF分量进行Hilbert分析，获取其局部Hilbert谱H′(ω,t)；

(4) 根据公式(7)和公式(8)求出每个样本信号的特征能量函数S(特征值)；

(6)按上述步骤计算出待检信号x(t)的特征值Sx，并求出其与标准特征值之间的M距离：

(9)

(7)比较di的大小，其中di的最小值所对应的状态即为被检测滚动轴承振动信号所处的工况。

4 试验研究

为验证此方法的正确性，在滚动轴承实验台上对不同工况(正常状态、内圈故障状态、外圈故障状态)滚动轴承的振动信号进行采集。实验台主要由信号发生系统、信号采集系统和信号分析系统等部分组成。

试验过程中，采样频率为 12kHz，电动机负荷为0，转速为1 797r/min，采样时间1s。滚动轴承内、外圈的故障原因为点火花加工所造成单点损伤。采集到的不同工况下滚动轴承加速度信号，如图1所示。

图1 不同状态下滚动轴承加速度信号

运用改进EMD对上述信号进行分解，其中，正常状态下滚动轴承信号分解得到5阶IMF分量，内圈和外圈故障信号经改进EMD分解都得到6阶IMF分量，其中不同状态下滚动轴承信号的各IMF分量与其原信号间的相关系数如表1所示。

表1 不同状态下各IMF分量与原信号相关系数

由表1可知，滚动轴承的主要信息集中在其前4阶IMF分量中，所以，对不同工况的滚动轴承振动信号，在此取IMF1～IMF4作为敏感IMF进行后续分析。不同故障状态下敏感IMF分量所求得的局部Hilbert谱示于图2。

图2 不同故障状态下滚动轴承加速度信号的局部Hilbert谱

由图2可知，当6205-2RS JEM SKF型滚动轴承出现故障时，激起的固有频率在2 000 Hz-3 000 Hz，因此，取ω1=2 000 Hz，ω2=3 000 Hz，求出的各状态下相应的标准特征值和方差var(Si)如表2所示。

表2 标准特征值和其方差

按照马氏距离判别方法的步骤对不同工况下滚动轴承的60组振动信号进行故障诊断研究，诊断结果表明：在正常状态和外圈故障状态下各出现1组误判，内圈故障状态下诊断结果全部正确，总体诊断正确率为96.67%，证明该方法在处理此类问题方面的有效性。而出现误判的原因可能是测量过程中的测量误差所造成的，部分诊断结果如表3所示。

表3 部分马氏距离函数诊断结果

5 结 论

(1)相较于传统HHT方法，将端点优化对称延拓的EMD方法同基于相关性分析的虚假IMF判别算法相结合的改进HHT方法可有效解决EMD分解过程中的端点效应和虚假模态问题，保证信号特征提取的准确性与有效性；

(2)通过M距离判别方法对局部Hilbert边际能量谱所提取的各IMF分量的能量特征参数进行滚动轴承的工作状态和故障类型识别，试验结果表明，该方法可有效识别出滚动轴承的故障类型和工作状态，为该类问题的解决提供了一种有效的方法。

[1] 褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法[M].北京：科学技术出版社,2009:159-160.

[2] 葛明涛，董素鸽.LMD及马氏距离敏感阈值的滚动轴承故障诊断[J].机械设计与制造,2015,2:210-213.

[3] 周小龙.希尔伯特-黄变换在故障诊断中的应用[D].长春：长春工业大学,2014.

[4] N.E.Huang,Z.Shen,S.R.Long,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proceeding of the Royal Society of London-Series A:Mathematical,Physical and Engineering Sciences,1998,454(1971):903-995.

[5] 游子跃，王宁，李明明，等.基于EEMD和BP神经网络的风机齿轮箱故障诊断方法[J].东北电力大学学报,2015,35(1):64-72.

[6] 周小龙，姜振海，马风雷.基于改进HHT的微弱故障信号特征提取方法[J].东北电力大学学报,2016,36(5):52-56.

[7] 王传菲，安钢，王凯，等.基于镜像延拓和神经网络的EMD端点效应改进方法 [J].装甲兵工程学院学报,2010,24(2):62-65.

[8] 雷亚国.基于改进Hilbert-Huang 变换的机械故障诊断[J].机械工程学报,2011,47(5):71-77.

[9] 黄诚惕.希尔伯特-黄变换及其应用研究[D].成都：西南交通大学,2006.

[10] 徐斌，徐德城，朱卫平，等.希尔伯特-黄变换方法的改进 [J].西北工业大学学报,2011,29(2):268-272.

[11] 于德介，程军圣，杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京：科学技术出版社,2006:154-166.

[12] 杨德友，蔡国伟.基于因散经验模式分解与最小二乘支持向量机的风电场短期风速预测 [J].东北电力大学学报,2015,35(3):44-49.

A Study of Rolling Bearing Fault Diagnosis Based on Local Hilbert Marginal Energy spectrum

Yang Gongyong1,Zhou Xiaolong1,Liang Xiuxia2,Li Jiafei2

(1.The Engineering Training Teaching Center,Northeast Electric Power University,Jilin Jilin 132012;2.Henan Xinyu Petroleum Machinery Manufacturing Company,Henan Puyang 457001)

Aiming at the non-linear feature of the rolling bearing vibration signal,a rolling bearing fault diagnosis method based on local Hilbert marginal energy spectrum and Mahalanobis distance is proposed.Firstly,the vibration signal is decomposed by improved empirical mode decomposition,and a set of the intrinsic mode function is obtained and the mode functions which containing the main fault information are selected by the false evaluation method based on correlation analysis technique.Then,energy characteristic parameters of fault signal are extracted from each IMF component by using local Hilbert marginal energy spectrum.Finally,Mahalanobis distance is used to identify the rolling bearing fault pattern.The experiment results show that this method can identify rolling bearing fault patterns effectively and offer a practical method for its fault diagnosis.

Empirical mode decomposition;Local Hilbert marginal energy spectrum;Mahalanobis distance;Rolling bearing;Fault diagnosis

2017-03-12

杨恭勇(1987-)，男，硕士，助理实验师，主要研究方向：机械制造及故障诊断.

1005-2992(2017)02-0077-05

TH17

A

电子邮箱： 76025858@qq.com(杨恭勇)；196389679@qq.com(周小龙)；2598037262@qq.com(梁秀霞)；2241430075@qq.com(李家飞)