对一道高考解析几何试题的再挖掘*
●庄俊辉 胡华叶(金华市第六中学 浙江金华 32100)
对一道高考解析几何试题的再挖掘*
●庄俊辉 胡华叶
(金华市第六中学 浙江金华 32100)
在数学高考中,解析几何问题因运算量大、思路不明确,学生易畏难.文章通过研究高考试题,发现需要抓住典型,深入研究、引申、推广,从而得到圆锥曲线的共同特点和相关结论,使高三数学的复习教学更有效,更有利于不同层次的学生有各自的收获.
一般化推广;充要条件;类比推广;变式拓展
解析几何大题是学生比较害怕的题目,主要是思路不明确、运算量大,造成成就感低,普遍有畏难情绪.最近,笔者在研究高考试题时发现解析几何题的破解,还是需要抓住典型,深入研究一些引申和推广,下面以2010年全国数学高考理科试题第21题为例进行说明.
题目 已知抛物线C:y2=4x的焦点为F,过点K(-1,0)的直线l与C相交于点A,B,点A关于x轴的对称点为点D.证明:点F在直线BD上.
1 一般化推广
将以上问题中的抛物线和点一般化,可得:
推广1 已知抛物线y2=2px(其中p>0),在x轴上有一点P(t,0)(其中t>0),过点Q(-t,0)的直线l与抛物线相交于点A,B,点A关于x轴的对称点为点D.证明:点P在直线BD上.
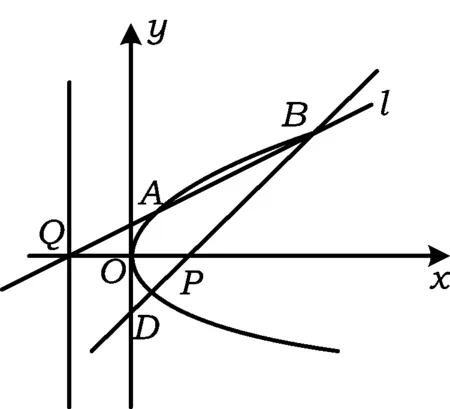
图1
证明 如图1,设A(x1,y1),B(x2,y2),由对称性知D(x1,-y1).将直线l的方程x=my-t(其中m≠0)代入y2=2px,得
y2-2pmy+2pt=0,
y1+y2=2pm,y1y2=2pt,
从而直线BD的方程为
即
令y=0,得
从而点P(t,0)在直线BD上.
2 充要条件
交换部分条件和结论,便产生一道新题,即:
推广2 已知抛物线y2=2px(其中p>0),过定点Q(-t,0)(其中t>0)的直线l与抛物线相交于点A,B,点A关于x轴的对称点为点D.证明:若直线BD与x轴相交于点P,则P为定点(t,0).
显然,由推广1的证明不难得出.
这种状况当然不适合有外人在场。但一切来得太快,也来得太突然,柳红想避已经避不开了,她像是被孙悟空定了身,傻傻地竖在苏秋琴面前。苏秋琴也如同从噩梦中惊醒,两眼惊恐地盯着她弟媳妇柳红。四目相对,犹如雷电相击,震得俩人赶紧别头,一个张东,一个望西。
综合推广1和推广2,可得:
推广3 已知抛物线y2=2px(其中p>0),在x轴上有一点P,过点Q(-t,0)(其中t>0)的直线l与抛物线相交于点A,B,点A关于x轴的对称点为点D.证明:点P在直线BD上的充要条件是P为定点(t,0).
3 类比推广
正如数学家波利亚感叹:“类比是伟大的引路人.”[1]我们知道抛物线与椭圆、双曲线具有部分统一性,椭圆、双曲线上是否具有抛物线上述类似发现?
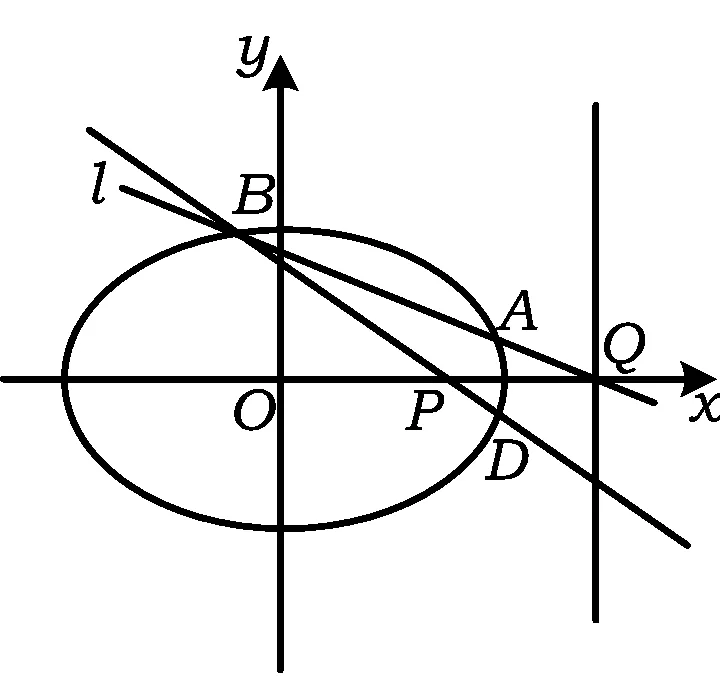
图2
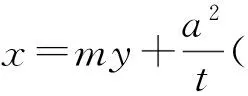
(a2+b2m2)t2y2+2mta2b2y+a2b2(a2-t2)=0,
(充分性)若P为定点(t,0),则
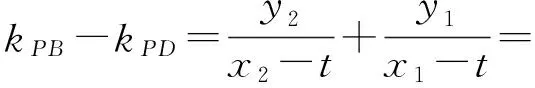
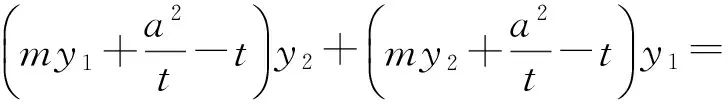
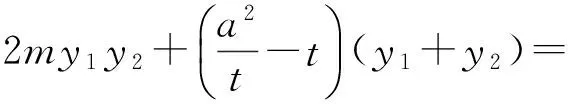
(必要性)不妨设点P(x0,0),则
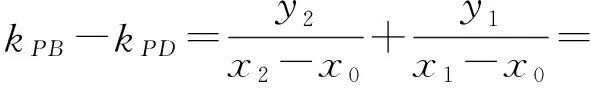
若点P在直线BD上,则kPB-kPD=0,即
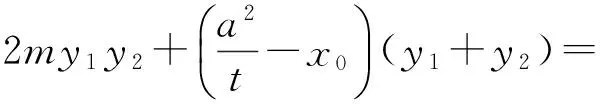
对于椭圆有推广4,对于双曲线是否也有同样的结论呢?答案是肯定的,证明方法与推广4基本相同,只需将椭圆发现证明过程中的b2换成-b2,便可得如下结论:
4 变式拓展
一道好的试题通常是命题者研究成果的结晶,它们在一个新的背景下,变换了部分条件和结论,或者是给出某个问题的一个特例,便又生成了一道新题,不断产生思维挑战.笔者又作了如下探究:
推广6 已知抛物线y2=2px(其中p>0),在x轴上有一点P(m,0)(其中m≠0),过点Q(n,0)(其中n≠0)的直线l与抛物线相交于点A,B,点A关于x轴的对称点为点D.证明:点P在直线BD上的充要条件是m+n=0.
探究一道好题,如饮美酒回味无穷;掌握一种方法,如获至宝爱不释手;理解一种思想,如登泰山绝顶,一览众山小.在新高考文理同卷的背景下,数学的复习教学更应该在有限的题目和时间里挖掘,以匹配不同层次的学生,让他们有各自的收获.
[1] 虞懿,曹斌.2015年高考数学全国Ⅰ理科第20题的探究历程[J].数理化解题研究,2016(4):18-19.
2017-02-28;
2017-03-30
庄俊辉(1983-),男,浙江金华人,中学二级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)05-25-02

