试验设计类型之可以考察部分交互作用的多因素设计：裂区设计

张效嘉，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

试验设计类型之可以考察部分交互作用的多因素设计：裂区设计

张效嘉1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

本文旨在介绍一种多因素试验设计方法，即裂区设计。从农业、工业、医学试验研究的实际出发，呈现了三个多因素试验的实例。进而总结出裂区设计具有的两个突出特点，即“一个完整试验被整批重复”和“试验因素施加于受试对象时存在先后顺序之分”。准确辨识一个多因素试验研究定量资料是否来自裂区设计，其意义在于是否需要选择裂区设计定量资料方差模型处理资料。

裂区设计；试验因素；区组因素；交互作用

1 裂区设计概述

裂区设计也叫做分割设计，顾名思义，就是把一个“整体”划分成几个长条，即所谓的“区组(英文为BLOCK)”或者把一个按时间排列的“过程”分割成几段，即所谓的“工序”。

不难想象，“裂区”的概念最早产生于农业试验研究中，研究者希望在一块农田或耕地上开展农业试验，考察在什么样“耕作方案”“种植方案”和“管理方案”的条件下产量最高。由于一大块试验田位于各个方位上的土壤质量(例如颜色、酸碱度、肥沃程度等)不尽相同，这种“本底情况”势必会影响产量。为了尽可能消除“本底”不同对结果评价造成的不合理影响，一个直观的想法就是把一整块田划分成很多中等大小的块(即区组)，假定共划分成k个中等大小的块，并假定这k个中等大小的块中的每一块内的“本底情况”基本接近。然后，再将每一中等大小的块划分成m个小块，这里的m就是全部拟考察的试验因素水平的全面组合数。于是，就相当于把一个多因素试验研究问题在k个中等大小的田块上做了k批独立重复试验。

同理，若要进行的试验研究工作需要在一个较长时间段内才能全部完成，假定需要在一周(共7天)内才能完成。此时，又可分为下列两种情形：

情形一，每半天就能完成全部试验因素水平的全面组合所对应的试验，但此项试验研究共需要重复做14个半天才能全部完成。实际上，这就相当于把前面“整个农田”“分块”一样，此时，只不过是把“整个时间长度”“分段”了。

情形二，全部试验因素不是一道施加的，而是分期分批施加的。举一个生活上的例子就很容易理解了。假定研究者希望烹饪出色香味俱全的菜肴，可能需要考虑到下列因素：炒锅加热的温度、油的品种和质量、菜的原材料的重量、菜下锅后被翻炒的频率、加水的重量(重量为0就是不加水)、是否盖锅盖、烹饪多长时间等。在这些因素中，它们应在两个阶段上被分别施加，即第一阶段涉及“炒锅加热的温度、油的品种和质量、菜的原材料的重量”三个因素；第二阶段涉及“菜下锅后被翻炒的频率、加水的重量(重量为0就是不加水)、是否盖锅盖、烹饪多长时间”四个因素。

把上面第二种情形的多因素试验设计叫做“分割设计”更合适；而把其他情况称为“裂区设计”更符合情理。

2 两种不同的裂区设计[1-2]

2.1 一个完整试验被整批重复

【例1】在某项试验中，涉及到药物种类和药物剂量，但试验需要在不同时间重复进行，显然，时间改变是较慢的，而在每个确定的时间点上，药物种类与剂量的水平改变都是很方便的。若用大鼠作为受试对象，可选取来自大鼠的重要非试验因素作为子区组因素，还可以不同日期做试验作为大区组因素，将药物种类与剂量进行组合构成析因结构，在以日期为大区组因素的各水平下，再以时间段和时刻为两层子区组因素，按含区组因素析因设计分配大鼠。设计见表1。

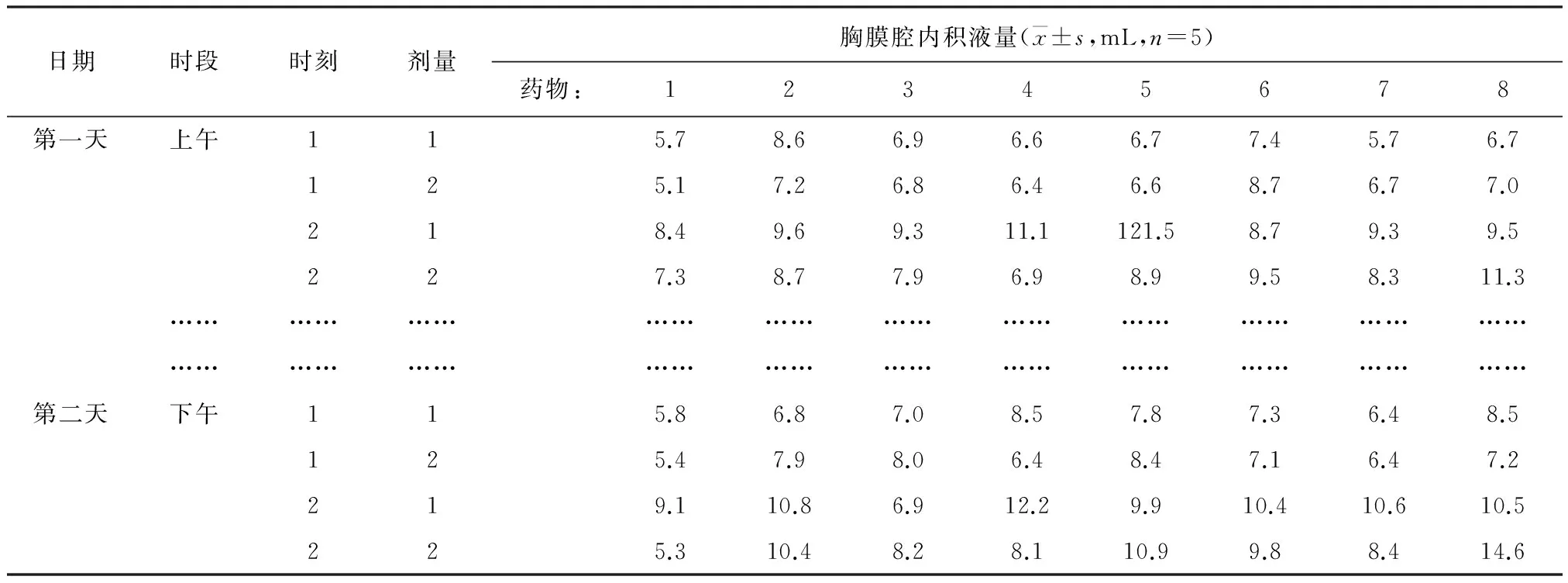
表1 不同药物、剂量和作用时间下大鼠胸膜腔内积液量

说明：第一行“……”代表省略了第一天下午的四行结果，第二行“……”代表省略了第二天上午的四行结果

【例2】研究者拟在一块地里进行燕麦产量试验。有三种燕麦(A)、四种肥料(B)，如何设计有利于消除地块位置不同对产量的影响？设计见表2。

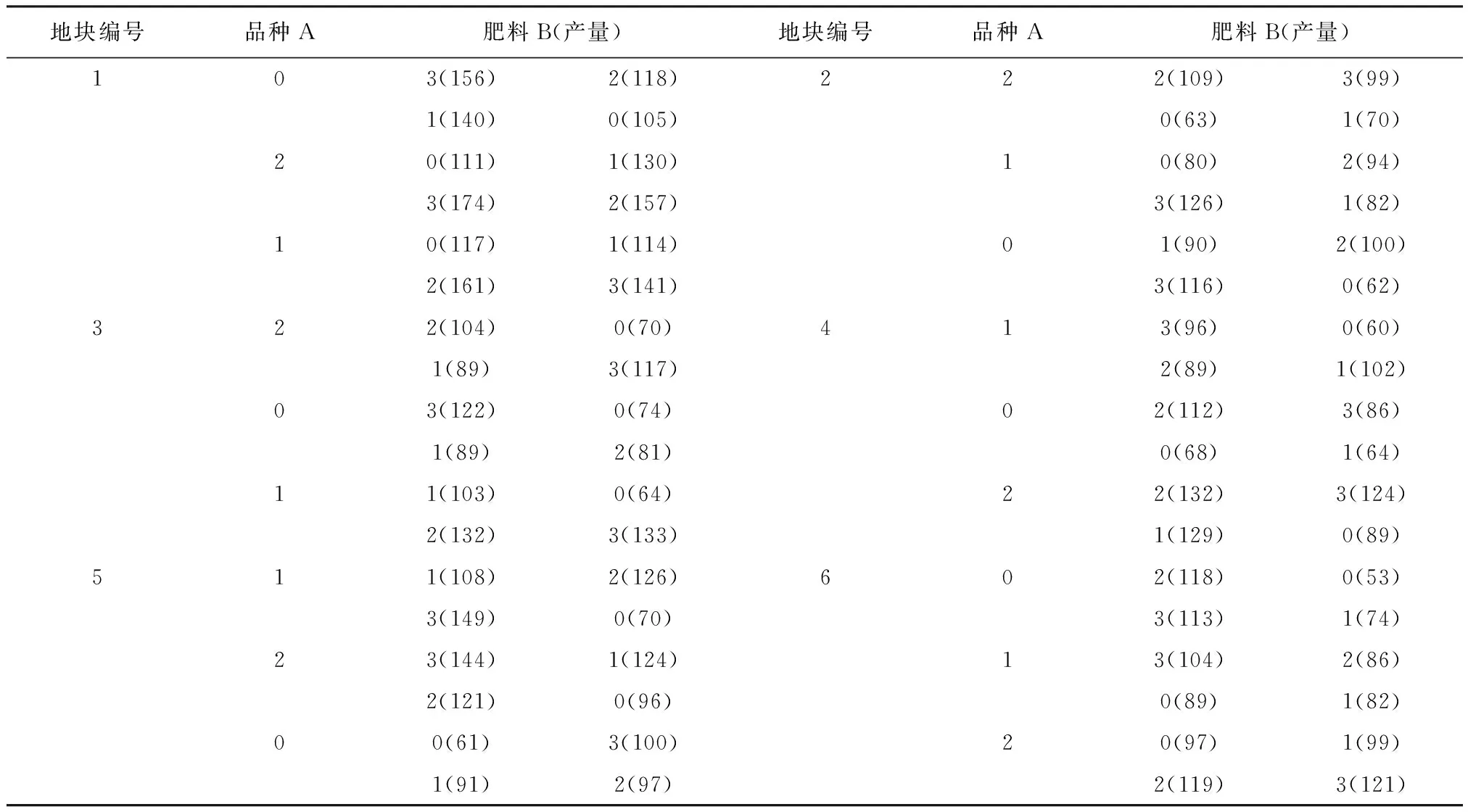
表2 燕麦产量(磅)

注：在原书中，第1块地里的品种从上到下为2、0、1，可能有误，此处作了调整

提示：整块地被分成6大块；每大块自北向南(表中可理解为自上而下)又被分成3中块；每个中块再被随机均分为4小块。“肥料”在小地块上被随机化安排，“品种”在中地块上被随机化安排，而“品种”与“肥料”的水平组合在大地块上被重复。

2.2 试验因素施加于受试对象时存在先后顺序之分

【例3】为研究不同瘤株的生瘤效果和不同浓度蛇毒的抑瘤作用，先将48只小鼠按原始体重分成3个随机区组(注：每个区组内的16只小鼠体重最接近)，将每个区组内的16只小鼠随机均分成4组，分别接种4种不同的瘤株，观察肿瘤生长情况。1天后再对接种同一种瘤株的4只小鼠分别腹腔注射4种不同浓度的蛇毒，连续用蛇毒抑瘤10天，停药1天后解剖测瘤重。设计格式和资料见表3，此为裂区(或分割)设计。

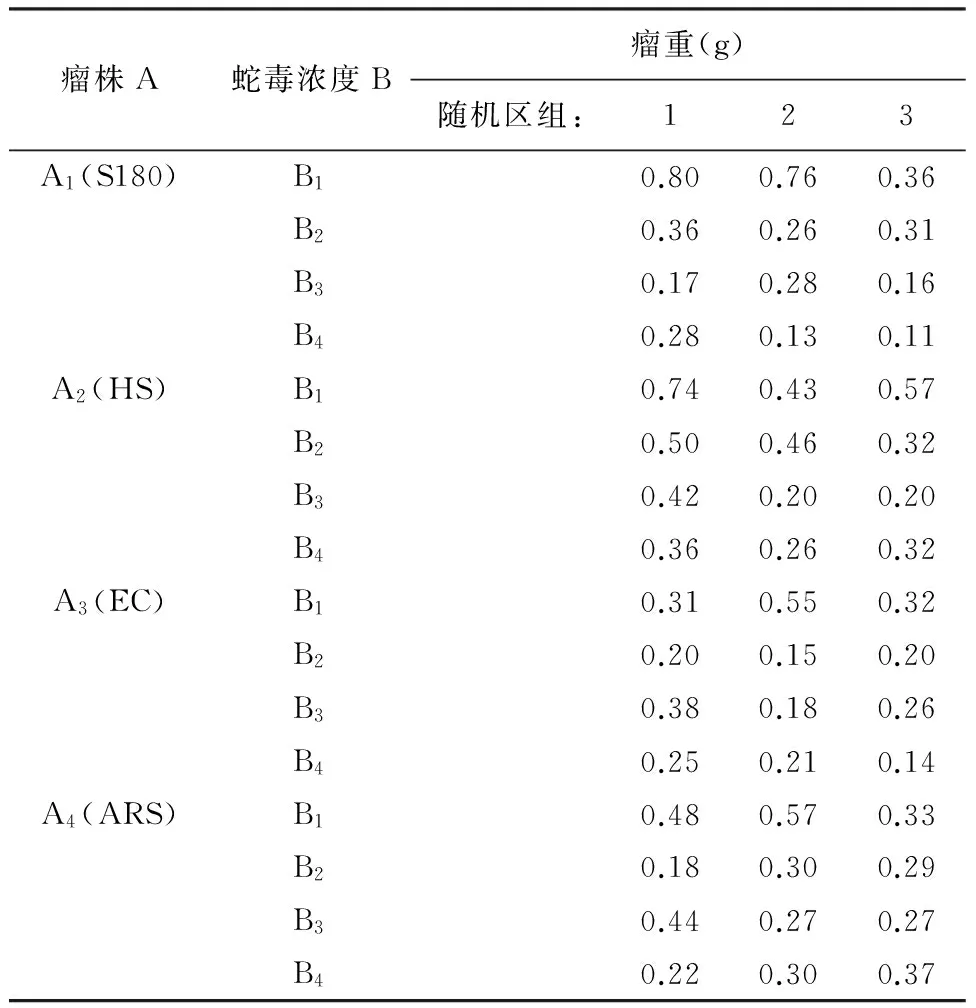
表3 不同瘤株与不同浓度的蛇毒共同作用后对小鼠抑瘤效果的影响

注：在本例中，瘤株先作用于受试对象，蛇毒后作用于受试对象

3 对上述两种裂区设计的解读

3.1 对表1所反映的实际问题的解读

在表1中，“时间因素”有三个不同名称，即“日期”“时段”和“时刻”，前者包含后者，它们都可被视为“区组因素”，而真正的试验因素“药物种类”与“剂量”，相当于把“药物种类”与“剂量”所决定的两因素析因设计分别在“时刻”“时段”和“日期”上进行重复。表1中的每个数据代表一个平均值，统计分析时应给出全部原始数据。这就是由“药物种类”与“剂量”两个试验因素决定的两因素析因设计结构沿着“时间轴”被整批地重复。

3.2 对表2所反映的实际问题的解读

在表2中，整块地被分成6大块；每大块自北向南(表中可理解为自上而下)又被分成3中块；每个中块再被随机均分为4小块。“肥料”在小地块上被随机化安排，“品种”在中地块上被随机化安排，而“品种”与“肥料”的水平组合在大地块上被重复。

3.3 对表3所反映的实际问题的解读

在表3中，“瘤株”和“随机区组”两个因素先出现在试验中，而“蛇毒浓度”是在施加“瘤株”后的第2天才施加的。显然，在这个试验中，“瘤株种类”与“蛇毒浓度”这两个试验因素在施加时确实有先后顺序之分。这就是一个完整的试验过程被划分成前、后两个阶段，在不同阶段上，有互不交叉的试验因素先后被施加进入试验。

4 运用裂区设计时应注意的两个事项

4.1 在分析裂区设计定量资料时，对不同阶段上的因素应区别对待

当因素按先后顺序施加，分析它们是否具有统计学意义的检验统计量的分母(即误差项)是不同的。出现在每个阶段上的因素，应基于该阶段上的“相应项”作为误差项。例如在前面的表3中，对于出现在第1阶段上的因素“瘤株”和“随机区组”而言，应选用“瘤株×随机区组”作为它们的误差项；而对于出现在第2阶段上的因素“蛇毒浓度”而言，则可以直接采用模型的误差项作为其误差项。

4.2 判定一个定量资料是否来自裂区设计的意义

其意义在于是否要按照裂区设计定量资料的方差分析模型去分析资料。因为裂区设计、嵌套设计、重复测量设计和析因设计等，都具有各自不同的方差分析模型。只有事先准确判定了拟分析的定量资料确实来自某种特定的多因素设计类型，才有可能正确地选定相应的方差分析模型对其进行处理。

[1] 胡良平. 统计学三型理论在实验设计中的应用[M]. 北京: 人民军医出版社, 2006: 89-93.

[2] 胡良平. 面向问题的统计学——(1)科研设计与统计基础[M]. 北京: 人民卫生出版社, 2012: 180-183.

(本文编辑：吴俊林)

Types of the multifactor experimental designs with partial interactions: split-plot design

ZhangXiaojia1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China; 2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

The paper aimed to introduce split-plot design which belonged to the multifactor experimental design. Three split-plot design cases in the agriculture, industry and medical trial field were presented in this paper. They indicated one complete experiment was entirely repeated as one of the characteristics of the split-plot design. Additionally, split-plot design was characterized by sequence of exerting experimental factors on subjects. Precisely identifying whether the quantitative data were from split-plot design may facilitate the selection of appropriate model of the analysis of variance to analyze the data.

Split-plot design;Experimental factor;Block factor;Interaction

国家高技术研究发展计划课题资助(2015AA020102)

R195.1

A

10.11886/j.issn.1007-3256.2017.02.003

2017-04-05)