基于小波包能量谱的钢轨扣件松脱检测研究*

周文静， 刘 冲， 韦佳宏， 张 凯， 张学海

(1.大连理工大学 机械工程学院，辽宁 大连 116024;2.大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024)

基于小波包能量谱的钢轨扣件松脱检测研究*

周文静1， 刘 冲2， 韦佳宏1， 张 凯1， 张学海1

(1.大连理工大学 机械工程学院，辽宁 大连 116024;2.大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024)

提出了基于小波包能量谱的钢轨扣件松脱识别方法，对获得的振动信号进行小波包分解，结合扣件松脱前后振动信号频域内能量变化，构造损伤指标(DI)。在此基础上，开展了5种工况下的轨道结构动力响应测试，进行了轨道结构状态识别分析。实验结果表明：DI能够有效地识别轨道结构状态，且随着松脱程度的增加而增加；同一工况下得到的损伤指标DI变化波动均在±0.5以内，验证了该方法具有很好的鲁棒性和抗干扰能力。

钢轨扣件； 振动信号； 小波包能量谱； 结构状态识别

0 引 言

扣件是连接钢轨与轨枕的重要部件，为钢轨提供扣压力确保钢轨不发生纵向和轴向偏移。随着高速铁路朝着高速重载化方向发展，在列车重复载荷作用下，轨道结构的轨下基础可能会产生破损，致使扣件松脱。一个扣件的松脱很容易诱发周围扣件的松脱，加剧轨道结构破坏，对列车行车安全将产生很大影响[1,2]。目前，扣件松脱检测主要有三种方法：1)基于人工巡检的方法，该方法效率低、成本高、容易漏检； 2)基于计算机视觉的方法[3]，该方法能够有效识别扣件是否缺失，但不能识别扣件的松脱程度，并且列车振动对图像质量有很大的影响； 3)基于振动信号的方法，文献[5]采用自功率谱密度的方法识别扣件松脱，该方法的灵敏度低，容易受输入激励的影响，扣件松脱识别结果不好。

近年来，随着小波包分析理论的发展，基于结构振动信号的小波包能量谱在结构损伤识别领域应用逐渐受到重视。刘涛等人[6]通过实验室模拟和数值分析验证了基于小波包能量谱的方法具有很高的结构损伤敏感性和测试噪声鲁棒性。孙君等人[7]通过对实测信号进行小波包能量谱分析，验证了该方法在实际环境激励下的结构损伤识别的有效性。葛继平等人[8]提出了基于小波包能量的累积变异指标对室内两跨连续梁进行损伤定位研究。余竹等人[9]提出了基于小波包能量曲率差法对梁体进行损伤识别研究，并通过数值模拟和现场实验验证了该方法能够有效地识别结构损伤。

以上损伤识别研究都是通过对振动响应信号进行小波包分解，利用损伤前后信号能量分布差异构造损伤指标。但在实际工程中很难保证以下两个问题：1)不同工况下的输入激励完全相同；2)不同工况下的激励点位置完全相同。本文在总结前人方法的基础上，提出了一种基于小波包理论和概率论统计学的方法，构造损伤识别指标(DI)，并研究了该方法在钢轨扣件松脱检测中的有效性和鲁棒性。

1 基于小波包能量谱的结构损伤识别方法

1.1 小波包能量谱理论

振动响应信号f(t)进行i层小波包分解，选择第i层小波包进行重构，根据相关性原理，选择前m个节点重构信号，确保重构信号与原始信号具有相同的主要频率成分[10]，则信号f(t)小波包重构信号表达式为

(1)

式中 di,j为第i层分解第j个节点的小波包分解重构信号，其对应的小波包节点能量Ei,j定义为

(2)

式中 Ei,j为第i层分解第j个频带的能量;N为信号数据长度。按照能量方式表示的小波包分解结果称为小波包能量谱，则信号f(t)的小波包能量谱向量E的表达式为

E={Ei,j}=[Ei,0,Ei,1,Ei,2,…Ei,m-1]

(3)

其对应信号f(t)的总能量为

Etotal=∑E

(4)

1.2 损伤指标的构建

由理论分析[11]可知，采用小波包能量谱中各个特征频带能量与所有频带能量的平均值之比作为结构损伤指标，将能更敏感地反映结构状态变化。第i层分解第j个特征频带的小波包能量比Ij定义为

(5)

将式(5)中小波包能量比Ij按照最大值进行归一化，然后将扣件松脱前后小波包能量比的相对变化量(energy relative variation，ERV)作为结构损伤判别基本参数，即

(6)

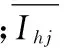
为了识别钢轨结构状态变化，在ERVj的基础上，定义能量比相对变化量偏差(energy relative variation deviation，ERVD)

(7)

结构在损伤前后的激励一样时，ERVD可以有效地识别结构损伤状态[6]。但在实际实验时，采用人工锤击法时并不能确保扣件松脱前后的激励相同，计算得到的ERVD会在一定范围内波动，造成钢轨结构状态的识别效果很差。因此，利用统计学理论计算不同工况下的ERVD的置信上限，将其置信上限作为结构损伤识别的指标。

根据数理统计理论[12]，ERVD服从t分布，其置信上限计算公式为

(8)

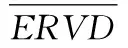
(9)

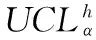
2 实验验证

2.1 实验设计

参照哈大客运专线技术标准搭建平台，总长为20.7 m，为防止钢轨受温度力影响发生轴向偏移将钢轨两端锁紧，扣件类型采用WJ—7型，扣件间距为630 mm，经测试该实验平台符合哈大客运专线施工验收标准规范。

2个单轴加速度传感器分别安装在钢轨两跨中间的轨头位置，采用力锤在轨头激励点位置处进行敲击，使用DHDAS—5902动态信号采集分析系统采集加速度信号，采样频率设置为10 kHz，测点位置分布如图1所示。定义扣件松脱个数百分比(即松脱程度)为某区域内扣件松脱个数占整个区域内扣件个数的百分比。本文分别模拟了5种工况下的扣件松脱实验，实验工况如表1所示，整个区域内扣件个数为4，工况1为4个扣件均是全紧状态(健康状态)，扣件松脱个数为0，松脱程度为0；工况2为松动扣件1，扣件松脱个数为1，松脱程度为25 %；工况3为同时松动扣件1和2，扣件松脱个数为2，松脱程度为50 %；工况4为同时松动扣件1,2,3，扣件松脱个数为3，松脱程度为75 %；工况5为同时松4个扣件，扣件松脱个数为4，松脱程度为100 %。每种工况采集次数均为70次，前60次实验作为计算样本，后10次实验作为测试样本，其中测试样本不参与计算样本DI值的计算。

表1 实验工况

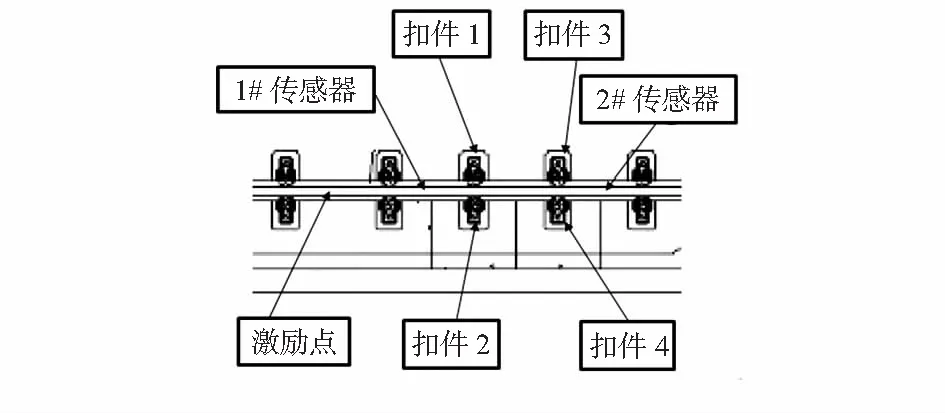
图1 测点布置图

2.2 实验结果分析

将1#和2#传感器采集的振动加速度信号进行7层dB40小波包分解，本文中取m=96时，重构信号和原始信号的相关性系数均达到了0.8以上。图2为2#传感器在5种工况下前60次实验时小波包ERV的平均值，从图中可以看出健康状态下(图2(a))的ERV与松脱状态下(如图(b)～(e))的ERV有明显有不同：健康结构下的ERV均小于1.2，而松脱状态下ERV在第8个频带时突变比较大，随着松脱程度的增加其ERV大小也逐渐增加。因此，频带能量比相对变化量ERV能够反映钢轨结构状态的变化，可以通过构造合适的损伤指标识别钢轨结构状态变化。

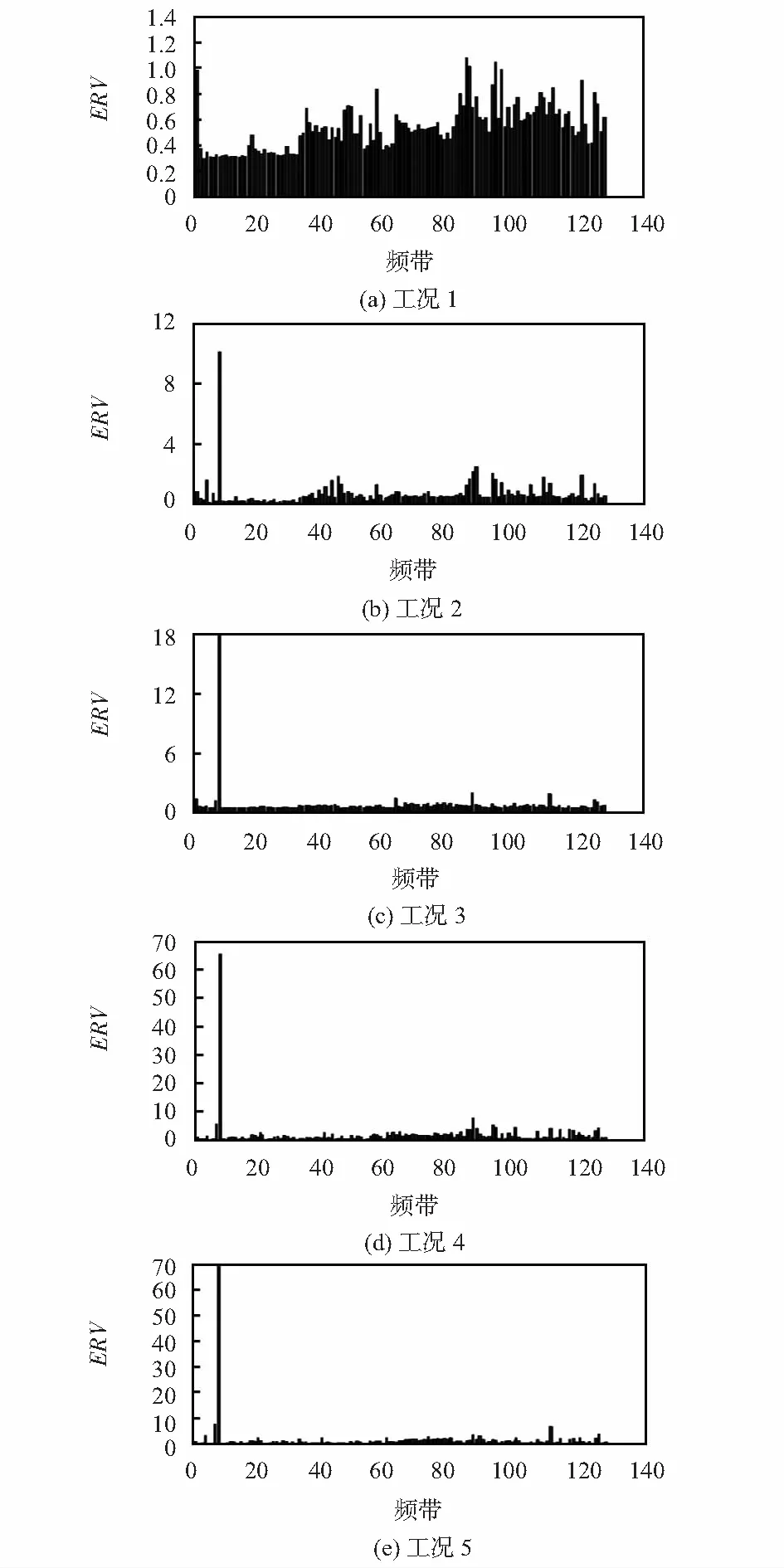
图2 小波包ERV的均值

将前60次健康结构下获得的能量比相对变化量ERV的平均值作为健康结构下的小波包ERV的基准，考虑到实际实验误差，选取能量比相对变化量偏差ERVD的置信度 为95 %，分位数λ通过t分布表插值得到2.001，按照式(7)～式(8)计算置信上限UCL，图3所示为1#和2#传感器在5种工况下的ERVD和UCL。从图3中可以看出：1)损伤工况下的ERVD总体上大于健康工况下的ERVD，且由于输入激励不同，ERVD在某一范围内波动，使不同工况下的ERVD有交叉的部分，因此，ERVD不能明显区分钢轨结构的各个损伤工况；2)相同传感器不同工况下的ERVD值不同，随着扣件松脱程度的增大ERVD整体上也逐渐增大，因此，ERVD可以在一定程度上反映结构状态变化；3)相同工况下，1#和2#传感器得到的ERVD和UCL不同，这是因为在实际实验过程中，并不能保证扣件松脱前后输入激励完全相同和传感器安装时位置相互对称；4)相同传感器不同工况下的置信上限UCL相对集中，且随着扣件松脱程度增大置信上限是逐渐增大的，因此，置信上限UCL在到一定程度上可以表征钢轨结构状态变化。

图3 传感器的UCL和ERVD

将图3所示的UCL代入式(9)，得到最终结构损伤指标DI，如图4为钢轨扣件松脱识别结果。从图4中可以看出：1)相同传感器不同工况下的DI值有明显差别，因此，损伤指标DI可以准确地识别钢轨结构的状态变化；2)相同传感器不同工况下的DI值有明显差异，随着扣件松脱程度的增大其DI值也逐渐增大，因此，DI值在一定程度上能够反映扣件松脱程度；3)在相同工况下，同一传感器前60次实验计算得到的结构损伤指标DI值在±0.5内波动，这说明了基于小波包能量谱的损伤指标对测试噪声具有很好的鲁棒性； 4)相同工况下，1#传感器的DI值要明显大于2#传感器的DI值，可见，靠近激励点位置的传感器得到的振动信号包含的损伤信息更为丰富，可以根据不同传感器得到的DI值大致判断结构损伤发生的区域。

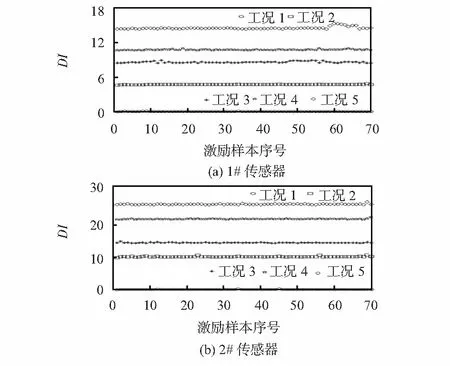
图4 传感器的损伤指标DI

3 结 论

实验结果表明：1)扣件松脱状态下的ERV和ERVD与健康结构下的指标有明显差异，这在一定程度上能够反映钢轨结构状态的变化；2)同一传感器不同工况下的结构损伤指标DI值有明显差异，且随着扣件松脱程度的增大而增

大，这在一定程度上能够反映钢轨结构状态的变化程度；3)相同工况下，同一传感器得到的结构损伤指标DI值在±0.5内波动，这说明了基于小波包能量谱的损伤指标DI对具有很好的鲁棒性和抗干扰能力。

[1] 肖新标，金学松，温泽峰.钢轨扣件失效对列车动态脱轨的影响[J].交通运输工程学报，2006(1):10-15.

[2] 翁长根，赫 丹，王 阳，等.扣件失效对城市轨道交通列车—浮置板式轨道系统竖向振动响应的影响[J].铁道科学与工程学报，2008(2):29-33.

[3] 王 凌，张 冰，陈锡爱.基于计算机视觉的钢轨扣件螺母缺失检测系统[J].计算机工程与设计，2011,32(12):4147-4150.

[4] 王文江，张 婧，李贤徽.轨道扣件松脱检测[J].噪声与振动控制，2013(z1):151-154.

[5] 刘 涛，李爱群，丁幼亮，等.基于小波包能量谱的结构损伤预警方法实验研究[J].振动与冲击，2009(4):4-9.

[6] 孙 君，李爱群，丁幼亮，等.润扬大桥悬索桥小波包能量谱识别的环境变异性[J].东南大学学报：自然科学版，2009(1):91-95.

[7] 葛继平，李胡生.基于小波包能量累积变异的梁桥损伤识别实验[J].振动、测试与诊断，2011(1):85-88.

[8] 余 竹，夏 禾，Goicolea J M，等.基于小波包能量曲率差法的桥梁损伤识别实验研究[J].振动与冲击，2013(5):20-25.

[9] 王 为，林玉池，赵美蓉，等.基于SPC与小波变换的光纤光栅型损伤识别[J].振动、测试与诊断，2011(5):566-569.

[10] 丁幼亮，李爱群，缪长青.基于小波包能量谱的结构损伤预警方法研究[J].工程力学，2006(8):42-48.

[11] 藤素珍,冯敬海.数理统计学[M].大连:大连理工大学出版社,2009.

Study on rail fastener loosening identification based on wavelet packet energy spectrum*

ZHOU Wen-jing1, LIU Chong2, WEI Jia-hong1, ZHANG Kai1, ZHANG Xue-hai1

(1.School of Mechanical Engineering,Dalian University of Technology,Dalian 116024,China; 2.Key Laboratory for Micro/Nano Technology and System,Liaoning Province,Dalian University of Technology,Dalian 116024,China)

A method based on wavelet packet energy spectrum is put forward to detect rail fastener loosening.Vibration signal is decomposed with wavelet packets,combined with energy variation in frequency domain before and after fastener loosening to build damage index(DI).On the above basis,conduct dynamic response tests of track structure under five conditions and identify and analyze on track structure state.Experimental results show that DI can effectively identify track structure state,which is significantly increasing with the increased degree of loosening;fluctuation range of DI under the same condition is within ±0.5,which proves that the proposed method has strong robust and capacity of resisting disturbance.

rail fastener; vibration signal； wavelet packet energy spectrum; structure state identification

10.13873/J.1000—9787(2017)05—0040—04

2016—05—14

国家“十二五”科技支撑计划资助项目 (2011BAG05B02—03,2011BAG05B02—02)

U 213.2

A

1000—9787(2017)05—0040—04

周文静(1990-)，女，硕士，研究方向为信号处理、故障诊断。

刘 冲，通讯作者，E-mail：chongl@dlut.edu.cn。