基于Lamb波群速度修正的复合材料结构损伤定位

高 飞，林 京，曾 亮

（1.西安交通大学机械工程学院，西安 710049；2.陕西省机械产品质量保障与诊断重点实验室，西安 710049；3.西安交通大学机械制造系统工程国家重点实验室，西安 710049）

相比于金属材料，复合材料具有高比强度和比模量、加工成型方便、耐化学腐蚀和稳定性好等优点，因此广泛应用于航空航天、武器装备等行业[1-2]。起初复合材料主要用于飞机的次承力结构，目前已逐渐向主要承力部件过渡。随着复合材料使用数量的增加及应用场合的增多，对复合材料安全性能的要求也变得更加苛刻。然而，复合材料结构在制造和服役过程中易产生肉眼不可见的损伤，如分层、脱粘和裂纹等[3],将造成材料性能大幅降低，给设备的安全运行带来巨大隐患。因此，对复合材料结构进行损伤诊断与维护具有重要的工程价值和经济效益。

当前常用的复合材料损伤检测方法有：超声法、射线法、热成像法和声发射法等。其中基于超声导波Lamb波的损伤检测被视为最具潜力的复合材料层合板的损伤检测方法之一。基于Lamb波损伤检测由于逐线扫描的检测方式而具有高检测效率，可实现结构大面积区域的在线检测[4]。同时，Lamb波的声场遍及整个结构，可实现对复合材料结构表面和内部损伤的识别。然而，Lamb波具有频散和多模态特性，接收信号十分复杂，给信号解析和损伤特征识别带来挑战[5]。此外，复合材料层合板的材料和结构特性又增加了信号的复杂度。因而，掌握Lamb波在复合材料中的传播特性是将其应用于损伤检测的前提。

针对Lamb波在复合材料中的传播特性研究，Lowe[6]根据层合板理论，建立了层状材料中的Lamb波的传播特性模型，进而计算出不同Lamb波模态的频散曲线；针对Lamb波在复合材料中的幅值调制特性，Giurgiutiu[7]通过理论和试验的方法计算了PZT压电传感器的可激励性幅值曲线，为模态选择和幅值调制分析提供理论依据；Schubert等[8]研究了复合材料中Lamb的衰减特性，获取了A0模态和S0模态的衰减曲线；针对幅值调制对响应信号波形的影响，Zeng等[9]研究了幅值调制对波形特征的影响机理，通过幅值补偿实现了损伤检测分辨率的提升。以上工作虽为Lamb波在复合材料层合板中的传播机理和检测提供了理论指导，然而幅值调制作用对于波包传播速度的影响尚未被关注。

为了研究幅值调制作用对窄带波包传播群速度的影响，提升损伤定位精度，本文以仿真和试验相结合的方法，以A0模态作为研究对象进行分析。首先通过试验研究获取幅值调制曲线，进而通过仿真信号阐述幅值调制对群速度的影响机制；然后，提出了基于幅值调制特性的群速度修正策略；最后，结合损伤定位方法，通过修正波包群速度以提高损伤定位精度。

Lamb波在复合材料中传播特性

Lamb波是由在薄壁结构中传播的横波和纵波耦合而成的弹性波。区别于金属板中Lamb波传播特性的求解过程，复合材料层合板中的Lamb波求解需考虑层数与铺层方向，通过全局矩阵方法计算Lamb波各模态的频散曲线[6]。Lamb波的不同模态具有不同特征，以A0模态为例，其对复合材料结构中常见的横向损伤相对敏感，且易于激励，因而被广泛用于复合材料结构损伤的检测，本文以A0模态作为研究对象。

本文的试验试件为树脂基碳纤维层合板（T300/3231），总铺层数为16层，单层厚度为0.125mm,铺层方向为[45/-45/0/90]2s，其材料力学特性如表1所示。通过理论计算，得到部分模态的相速度频散曲线，如图1（a）所示。为了验证理论计算结果的有效性，通过试验方法求取了部分频带的A0模态的群速度曲线。A0模态的群速度理论曲线和试验验证结果如图1（b）所示。由理论与试验结果对比可知，理论计算与试验数据具有一致性。

频散和多模态为Lamb波主要特征。频散指Lamb波的相速度随频率的变化而不同，导致接收信号随传播距离的增加在时域中扩散，给信号的解析和损伤检测分辨率带来不利影响。多模态指在任意激励频率下，存在至少两种及以上的导波模态。在低频情况下，A0模态与S0模态通常共存。为了降低信号的复杂度、抑制频散和多模态，导波检测过程通常采用窄带信号作为激励，其中正弦加窗信号被广泛用于基于Lamb波的损伤检测的激励。图2为常用的激励信号及对应频谱案例（中心频率为50kHz的5周期正弦加窗信号）。可知，正弦加窗信号的主要能量集中在有限带宽内，能量在带宽内分布对称且在中心频率处幅值最大，因而最大频谱幅值（定义为能量中心）对应的频率为中心频率。通常在计算传播距离时，采用中心频率处的群速度作为波包的传播速度。

表1 碳纤维板材料特性

图1 复合材料层合板中Lamb波的速度频散曲线Fig.1 Dispersion curves for Lamb waves in composite laminates

幅值调制对信号频谱影响

假设激励信号为f（t）,则Lamb波的传播过程可以表达为：

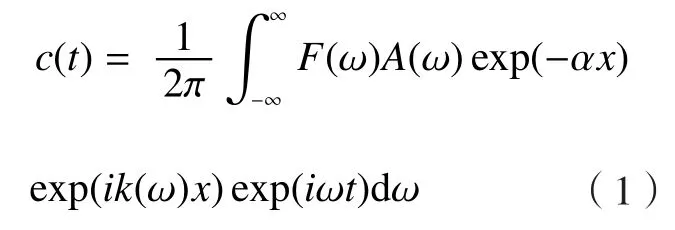
式中，F(ω)表示激励信号的傅里叶变换；A(ω)表示模态可激励性幅值调制；α表示粘弹性衰减系数，表征粘弹性衰减；k(ω)为波数，表示导波模态的频散信息。

幅值调制将改变信号的有效频带和频谱能量分布，使得信号发生变异。由公式（1）可知，幅值调制包含模态可激励性调制和衰减调制。为了探究复合材料中幅值调制对信号的改变程度，本文通过试验方法[10]获取了基于PZT激励的Lamb波A0模态的可激励性曲线及衰减系数曲线。Lamb波可激励性曲线通过激励幅值相同、中心频率变化的正弦加窗信号，提取直达信号包络峰值而获得，得到的A0模态的结果如图3（a）所示。可知，对于PZT激发出的Lamb波，A0模态可激励性幅值调制使得A0模态的能量分布集中在110kHz以下，且幅值最大处位于频率55kHz。为保证信号的信噪比，若使用A0模态作为激励，其激励信号的中心频率应选择幅值占优的频带范围内。

衰减系数的试验求取方法为布置距离一定的两个接收传感器，激励与接收之间距离分别为x1和x2，提取对应不同中心频率下接收的信号幅值最大值，分别为R1和R2，通过以下公式可计算衰减系数随频率变化曲线：

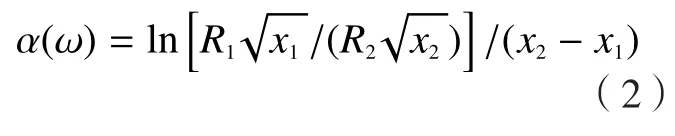
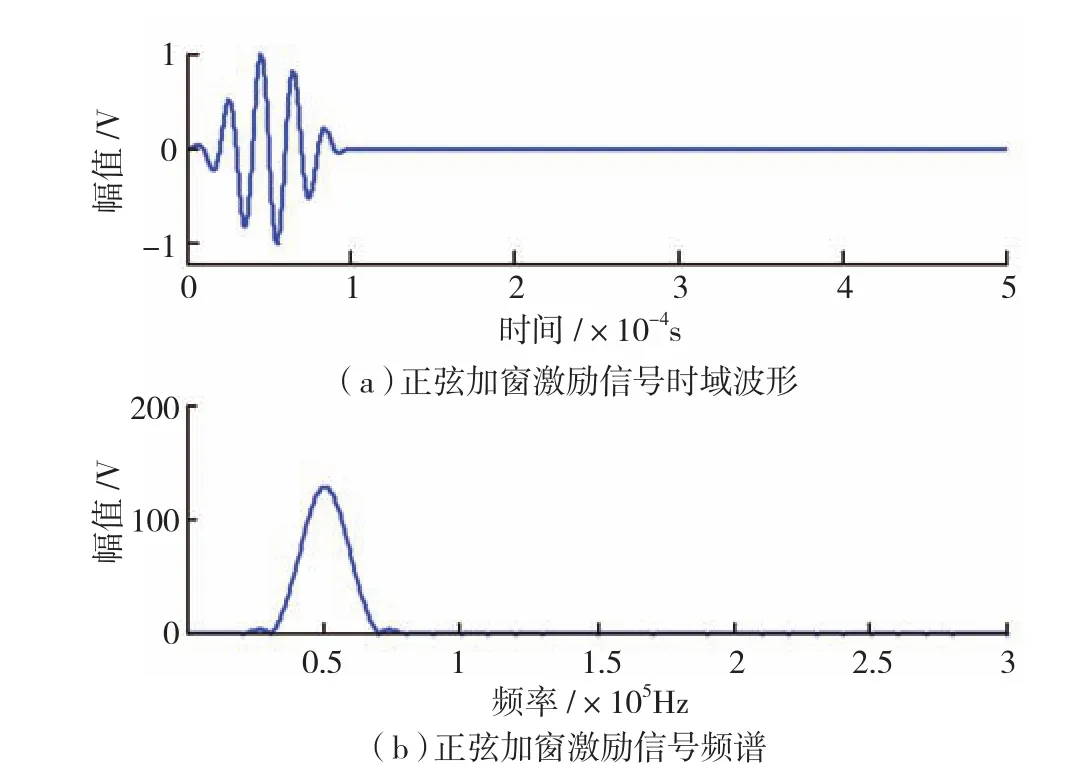
图2 正弦加窗激励信号及其频谱Fig.2 Windowed excitation signal and its spectrum

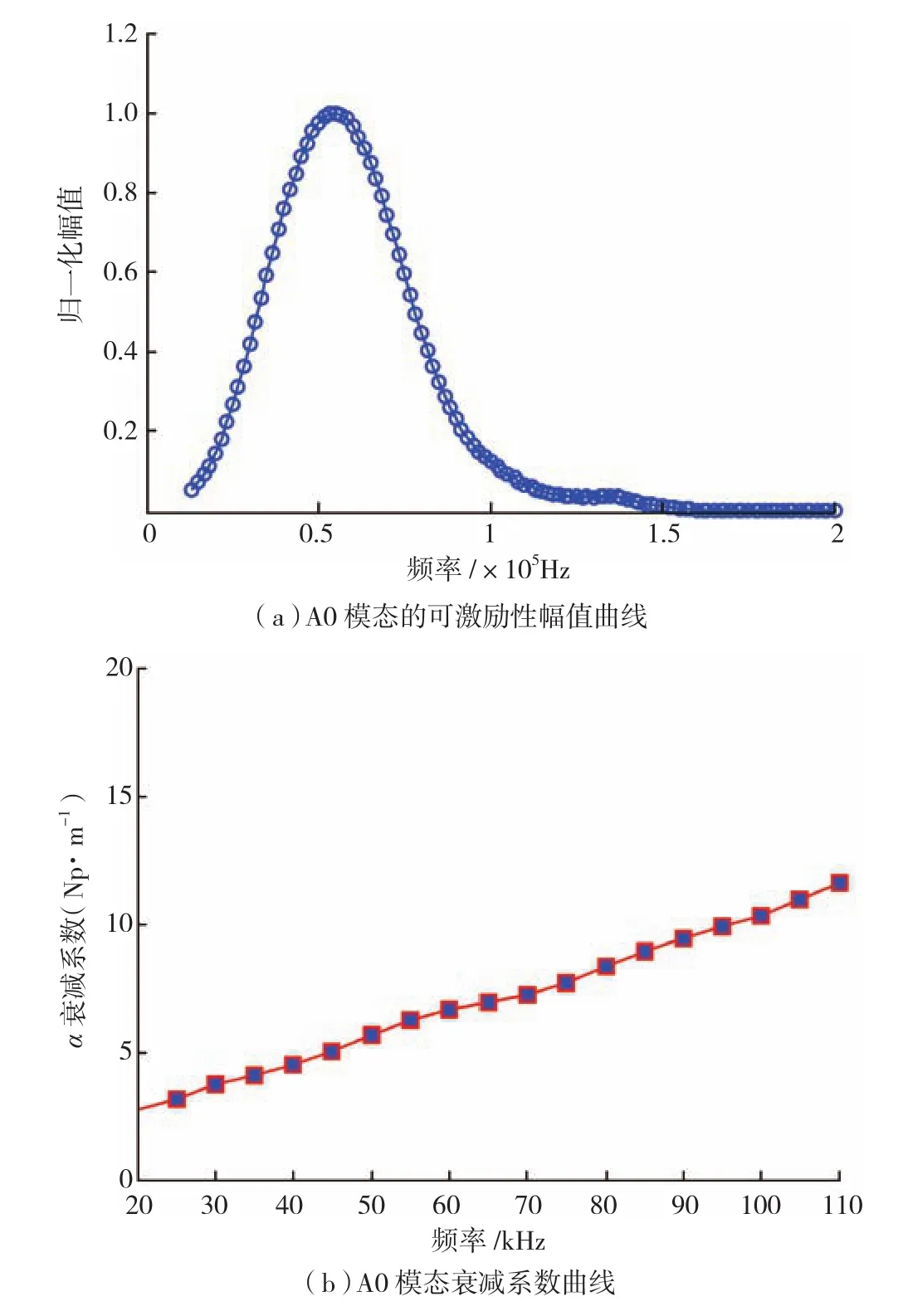
图3 A0模态幅值调制曲线Fig.3 Amplitude modulation curves for A0 mode

对A0模态信号进行分析计算，提取传播距离分别为50mm和200mm时的A0模态幅值，计算得到的20～110kHz频带范围内的衰减系数如图3（b）所示。A0模态的衰减随频率的增加而近似线性增长，即频率越高衰减越强。

为了探究幅值调制对接收信号的影响，尤其是群速度变化影响，本文根据先验的模态可激励性曲线和粘弹性衰减曲线进行波形仿真，以此说明能量中心的偏移及其对波包传播的影响。本文中的仿真以公式（1）所描述的导波传播模型为根据，将理论计算和试验研究得到的频散曲线、可激励性幅值曲线和衰减曲线作为参数，通过设计不同的激励信号和接收参数，进而计算得到响应信号。

以中心频率为70kHz的3脉冲正弦加窗信号作激励信号为例，仿真信号受到幅值调制后（包含可激励性幅值调制与衰减调制）的波形，传播距离分别为0.3m、0.5m、0.7m。幅值调制后的波形与未调制的波形对比分别如图4所示。其中，蓝色线为仅频散作用下的接收信号波形，红色线为经幅值调制后的信号波形。可以发现，经过幅值调制后的波形，其波包随着传播距离的增加越来越滞后于蓝色波形，简而言之，波包的群速度相比于中心频率处群速度发生明显降低。由此可见，将激励信号中心频率对应的群速度用于距离估算得到的结果将不再准确。

对幅值调制后的信号进行幅值谱分析，分别分析可激励性幅值调制及衰减调制作用。图5（a）所示的中心频率分别为30kHz、50kHz及70kHz对应的激励信号频谱及对应的可激励性幅值调制后的信号频谱。由结果可知，受激励性幅值调制影响，实际的激励信号的频谱幅值分布发生变化，峰值对应频率将不再位于激励中心频率位置。对于上述3种激励经调制后的结果，峰值对应频率分别为35kHz、51.5kHz及62.5kHz。因此，传感器的可激励性幅值调制对信号的能量分布作用明显，且经过可激励性幅值调制后，信号的能量分布不再对称，因此波包能量中心将不能再以激励信号的中心频率作为代表。

衰减是另一幅值调制的重要因素，仿真经可激励性幅值调制后的中心频率为70kHz的激励信号，在传播距离分别为0.3m、0.5m和0.7m的情况下的频谱。粘弹性衰减系数如图3（b）所示，仿真结果如图5（b）所示。随着传播距离的增加，粘弹性衰减影响频谱能量分布往低频迁移，根据仿真可以看出峰值对应的频率由70kHz分别变为57kHz、53kHz和49.5kHz。

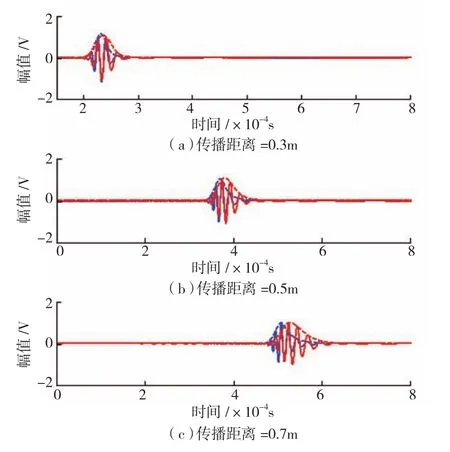
图4 幅值调制前后的接收信号波形对比Fig.4 Waveforms with and without amplitude modulation

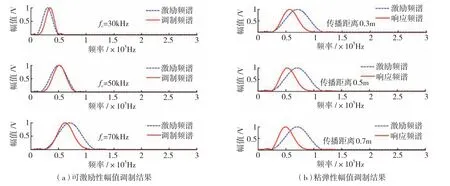
图5 幅值调制后的频谱结果Fig.5 Spectrum results with amplitude modulation

综上所述，由传感器可激励性调制和粘弹性衰减综合作用的幅值调制将改变信号的能量分布，能量中心将发生偏移。传统的以中心频率处群速度作为波包传播速度将不再准确，给复合材料中的Lamb波传播距离估计带来误差，进而影响损伤定位精度。因此，基于幅值调制的机理研究，选择合适群速度用于传播距离估计是提升复合材料结构损伤定位精度的重要手段。

基于群速度修正的损伤定位成像

在幅值调制的研究基础上，本文以可激励性幅值调制曲线及粘弹性衰减曲线为先验知识，以频谱能量分布中的峰值对应频率（能量中心）作为群速度选择频率，并将以此频率对应的速度作为速度修正参数。由于传感器可激励性幅值调制对于特定的传感器是恒定的，因此对于以中心频率为fc的激励信号而言，实际频域能量中心可以通过寻找A(ω)F(ω)的最大值处频率获得，设为f0。此外，对于粘弹性衰减引起的幅值调制作用，若已知传播距离为x，则可理论计算粘弹性幅值调制对频率的调制作用。

为了修正幅值调制带来的速度变化，本文以接收信号的目标波包的能量中心对应频率fx为另一频率参数进行修正速度的确定，考虑到粘弹性幅值调制引起的频谱能量偏移随距离的增加而增加，因而接收频率fx是传播距离的函数，为了降低计算难度，本文近似认为群速度为频率f0和频率fx对应群速度的均值，可以表示为：

综上所述，群速度修正过程可以总结为：首先考虑传感器可激励性幅值调制作用，进行调制幅值响应曲线计算，得到f0；而后，根据传播距离x，计算因粘弹性幅值调制导致的能量偏移，得到对应频率fx；最后，根据公式（3）计算得到中心频率为fc下的关于变量x的修正速度。实际中，传播距离x难以事先获取。然而，在延时叠加算法中，为了对损伤进行位置估计，常将检测区域划分为若干网格，若所划分的网格中出现损伤，则在接收信号中会产生相应的反射波包。通过扫描不同网格，获得每个网格对应传播距离，再以传播速度为载体建立幅值与损伤指标关系，进而判定损伤位置。因此，群速度修正结果对于基于延时叠加算法的损伤定位结果极为重要，且基于距离的群速度修正也符合定位计算要求。

基于上述原理，本文提出了基于群速度修正的延时叠加改进定位算法，相比于传统算法[11]，不同之处在于其传播时延的计算将使用修正后的群速度。首先划分的网格根据其与激励和接收传感器的相对距离，计算通过每个网格的波传播路径的距离；进而计算fx及其对应的群速度值，得到修正群速度值；再以多组信号的反射信号包络幅值作为损伤指标，通过时域信号中的时延与修正群速度建立信号与损伤信息的对应关系。

具体地，以压电陶瓷晶片（PZT）用于Lamb波的激励和接收，假设传感器对Tij的接收信号的Hilbert包络幅值为Rij(t)，Lamb波由传感器i激励。若经过像素点(x,y)产生反射信号，由传感器j接收，则此时的特征距离为Dij(x,y)， 对应的修正后群速度可通过公式（3）所得，则得到的检测区域各个像素点的像素能量强度值P(x,y)：

式中，V为窄带信号的群速度修正值。P(x,y)以幅值信息作为表征,表示反射源位于(x,y)处的可能性。

试验验证与结果讨论

1 试验设置

为了验证基于群速度修正的损伤定位方法的有效性，本试验以T300/3231碳纤维复合材料层合板作为试件，其尺寸为700mm×700mm×2mm,材料特性和铺层如表1所示。检测系统包含Agilent 33220A任意波形发生器、NF-HSA 4012功率放大器、压电陶瓷晶片（PZT）以及安捷伦的DSOX3014A数字存储示波器。在复合材料表面上布置4个PZT传感器组成的阵列，每个传感器可作为激励和接收。图6所示为基于Lamb波的检测系统。数据采集过程PZT传感器依次作为激励，其余PZT传感器作为接收。传感器坐标依次为(0,0)mm，(280,0)mm，(280,280)mm和(0,280)mm。损伤采用磁铁双面吸附进行模拟。损伤位置坐标为(100,150)mm，模拟损伤的直径为10mm。采样频率为5MHz,数据点数为10000个点。

图6 试验设置Fig.6 Experimental setup

2 结果与讨论

激励信号选择为中心频率70kHz的三脉冲正弦加窗信号，为了凸显损伤反射信号，损伤引入前后分别采集无损伤下的基准信号和损伤信号，通过残差得到损伤反射信号。以PZT4作为激励为例，PZT1接收到的参考和损伤信号及残差信号分别如图7所示。结果显示，仿真损伤能够产生反射波包，且残差信号能够凸显反射信号，为损伤定位提供信息支撑。类似地，可以计算所有传感器对的残差信号用于损伤定位。

为了获取对应于损伤传播距离的修正速度，根据试验获取的可激励性幅值调制曲线及粘弹性衰减调制曲线，可计算得到传播距离与能量中心的对应关系。本文以中心频率70kHz的A0模态信号为例，根据公式（3）可计算得到峰值频率与传播距离和修正速度与传播距离的对应关系曲线，如图8所示。

由结果可知，随着传播距离的增加，A0模态的高频衰减要强于低频，使得响应信号的频谱能量随着距离增加往低频偏移，对于中心频率为70kHz的激励信号，受到幅值调制后的能量中心显著降低。此外，根据文中提出的群速度修正方法，得到的A0模态的修正速度依然与传播距离相关，其修正速度随着传播距离的增加逐渐减小。由理论速度曲线可知，70kHz对应的群速度为1437m/s，然而随着传播距离增加，速度下降明显。

为定位模拟损伤位置，将280mm×280mm的检测区域划分成400×400的网格，每个网格均为大小一致的正方形。计算每个网格相对传感器对的传播距离，进而为每个网格挑选对应的修正速度。通过传播距离与修正速度的比值获取对应时延，提取残差包络响应的幅值作为损伤指标。最终以成像结果中网格数值最大处的位置作为损伤识别位置，计算结果如图9（a）所示。作为对比，以中心频率处的群速度值计算得到成像结果及定位结果如图9（b）所示。损伤的计算坐标分别为(95.5,158)mm和(85,166.5)mm。由定位结果可知，未经群速度修正的定位结果误差为2.24cm，而经过速度修正后的定位结果误差为0.9cm。可见对速度进行修正后能够得到更为准确的损伤定位结果。此外，使用修正后的速度进行定位仍存在定位误差，其原因为计算过程中引入的群速度的计算误差和模拟损伤的尺寸带来的几何误差。

图7 PZT4激励/PZT1接收信号及其残差信号Fig.7 Signals for PZT4 actuating and PZT1 receiving

图8 fc=70kHz时A0模态修正曲线Fig.8 Correction curves for A0 mode with fc=70kHz

图9 损伤成像结果对比Fig.9 Damage localization results

结论

（1）复合材料中的Lamb波传播受幅值调制的影响将发生波形畸变，一方面改变响应信号的有效带宽，另一方面改变信号在频谱中的能量分布。此时频谱能量中心将产生偏移，能量偏移过程受传感器可激励性幅值调制和粘弹性衰减幅值调制共同作用。根据试验研究结果，可以获得较为准确的幅值调制曲线，进而为频谱能量偏移提供定量信息分析支持。

（2）由于信号频谱能量的偏移，传统使用中心频率处的群速度计算传播距离将不再准确。本文使用能量中心对应频率作为速度选择指标，分别考虑两种幅值调制带来的频谱偏移结果，提出了速度修正方法。根据此方法，可以根据传播距离的变化找出对应的群速度。此方法可用于延时叠加定位算法的改进，得到更加精确的定位结果。

[1]杜善义. 先进复合材料与航空航天[J].复合材料学报, 2007, 24(1):1-12.DU Shanyi. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007, 24(1): 1-12.

[2]杜善义, 关志东. 我国大型客机先进复合材料技术应对策略思考[J]. 复合材料学报, 2008, 25(1):1-10.DU Shanyi, GUAN Zhidong. Strategic considerations for development of advanced composite technology for large commercial aircraft in China[J]. Acta Materiae Compositae Sinica, 2008, 25 (1):1-10

[3]BEAUMONT P W R. The failure of fibre composites: an overview[J]. Journal of Strain Analysis for Engineering Design, 2007,24(4):189-205.

[4]SU Z, YE L. Identification of damage using lamb waves[M]. London: Springer, 2009.

[5]ROSE J L. Ultrasonic guided waves in solid media[M]. Cambridge: Cambridge University Press, 2014.

[6]LOWE M J S. Matrix techniques for modeling ultrasonic waves in multilayered media[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 1995,42(4):525-542.

[7]GIURGIUTIU V. Lamb wave generation with piezoelectric wafer active sensors for structural health monitoring[J]. Proceedings of SPIE—The International Society for Optical Engineering, 2003, 5056:111-122.

[8]SCHUBERT K J, HERRMANN A S. On attenuation and measurement of Lamb waves in viscoelastic composites[J]. Composite Structures, 2011, 94(1)： 177-185.

[9]ZENG L, LIN J, HUANG L, et al. Amplitude dispersion compensation for damage detection using ultrasonic guided waves[J]. Sensors, 2016(16), 1623. doi:10.3390/s16101623.

[10]LIN J, GAO F, LUO Z, et al. Highresolution lamb wave inspection in viscoelastic composite laminates[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11):6989-6998.

[11]MICHAELS J E, HALL J S,HICKMAN G, et al. Sparse array imaging of change-detected ultrasonic signals by minimum variance processing[C]//AIP Conference Proceedings, 2009, 1096(1): 642-649.