让错因现形和错误拜拜

让错因现形和错误拜拜

封涛

小明是个学习数学积极努力的学生，但最近他在数学学习中遇到了麻烦跑来向老师求助，怎么回事呢？原来啊，他在解决图形变化问题时总是出现一些错误，这让他烦恼不已，那么在解决图形的变化问题中通常会有哪些错误呢？又有哪些注意点呢？我们不妨针对小明的错误一起来“诊断”一下吧.

一、概念学不透

例1如图1，在网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠OAB的正弦值是.

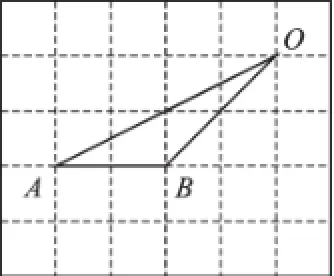
图1

【错因分析】一个角的正弦值应该在直角三角形中用对边比斜边，而△AOB不是直角三角形，所以不可以直接用OB OA，应该先构造一个直角三角形再求解.

【正确解答】如图2，过点O作OC⊥AB的延长线于点C，则AC=4，OC=2，在Rt△ACO中，AO=2，所以

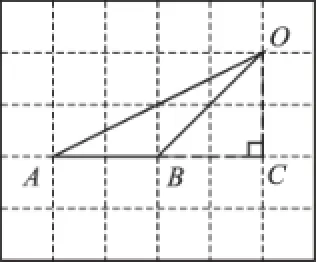
图2

【小结反思】在概念学习时一定要掌握概念的本质特征，对概念的理解不能浮于表面，否则容易出错.

二、情况想不全

例2已知，在直角坐标系中，有点E（-4，2），F（-1，-1），以O为位似中心，按比例2∶1把△EFO缩小，则点E的对应点E′的坐标为.

【小明解答】（-2，1）.

【错因分析】本题考查了位似的相关知识，位似是特殊的相似，位似比等于相似比.但在解决位似问题时常常要注意位似的两种情况，即位似图形在位似中心的同侧或者异侧.

【正确解答】（2，-1）或（-2，1）.

【小结反思】数学解题中常常会出现一个问题需要考虑几方面的情况，也就是我们经常说的分类讨论思想，大家一定要熟练掌握.

三、规律找不对

例3在同一坐标系中，图形a是图形b向上平移3个单位长度得到的，如果图形a上点A的坐标为（4，-2），则图形b上与点A对应的点A′的坐标为.

【小明解答】（1，-2）.

【错因分析】本题考查了坐标与图形变化中的平移，图形平移后点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减.所以图形b向上平移应该是横坐标不变，纵坐标变化，同时这里还要注意，是由平移后的图形反过来求原图形的坐标.

【正确解答】（4，-5）.

【小结反思】准确审题，是通向成功的开始；掌握规律，是解决问题的保障.

四、知识用不活

例4用小正方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体最少需要正方体个数为（）.

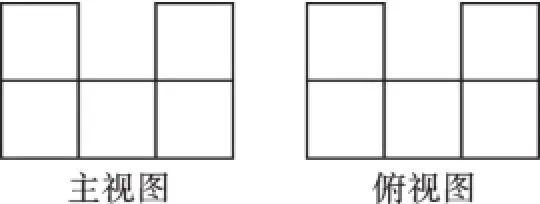
A.7B.8C.9D.10

【小明解答】C.

【错因分析】本题考查了三视图掌握程度和空间想象能力.由俯视图可以得最底层小正方体的个数及摆放方式，从主视图可得每列小正方体的层数和个数，但因求正方体最少的个数，所以在满足两个视图的前提下，将不必要的正方体去掉.如果理解口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案.

【正确解答】A.

【小结反思】在解决问题的过程中一定要灵活运用所学知识，有时可以自己归纳一些方法和技巧，有利于解决同一类问题.

五、关键抓不住

例5如图3，在平行四边形ABCD中，点E为AB的中点，F为BC上任意一点，把△BEF沿直线EF翻折，点B的对应点B′落在对角线AC上，则与∠FEB一定相等的角（不含∠FEB）有（）.

图3

A.1个B.2个C.3个D.4个

【小明解答】A.

【错因分析】本题考查翻折变换（折叠问题）和平行四边形的性质等知识，在找相等角时不仅要根据对称直接得角相等，还有由边相等得角相等，由中点分析出EA=EB′是正确解答此题的关键.

【正确解答】D.

【小结反思】在解决问题时，常常一个隐含的条件和结论会成为最终解决问题的关键，本题隐含EF∥AC的结论，包含基本图形组合：角平分线、等腰三角形、平行线.我们需要细心观察，耐心分析，用心积累.

六、图形看不出

例6平面直角坐标系中，O为坐标原点，点A的坐标为（3，1），将OA绕原点按逆时针方向旋转90°得OB，则点B的坐标为（）.

A.（1，3）B.（-1，3）

C.（-3，1）D.（-1，-3）

【小明解答】C.

【错因分析】本题主要考查坐标与图形变化中的旋转，在解题时一定要看出图形特征,选择合适的方式来解决问题.譬如这儿将OA绕原点按逆时针方向旋转90°得OB后可以用“双垂线”法构造全等三角形，利用全等三角形性质求出对应线段长度，进而求出点B的坐标.

【正确解答】如图4，过A作AC⊥x轴，过B作BE⊥x轴.易证△OCA≌△BEO，所以OE=AC= 1，BE=OC=3，所以点B坐标为（-1，3）.

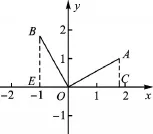
图4

【小结反思】平时解题一定要善于积累基本图形，这样在解决一些综合问题时往往能从复杂图形中迅速看出或构造出熟悉的基本图形，从而找到解决问题的办法.

（作者单位：江苏省泰兴市洋思中学）