关注“模型教学” 提升“思维品质”——“半角模型”中考试题归类赏析及启示

姜晓翔

（浙江省湖州市南浔区教育教学研究和培训中心）

关注“模型教学” 提升“思维品质”
——“半角模型”中考试题归类赏析及启示

姜晓翔

（浙江省湖州市南浔区教育教学研究和培训中心）

近几年的各地中考试卷中逐渐涌现出由同一类“基本模型”延伸而来的试题，这些试题虽各不相同，但解决问题的方法、策略相通.这就势必要求教师通过研究试题来挖掘并提炼各类“基本模型”，从而抓住学生思维“生长点”，寻求思维“延伸点”，追求思维“发散点”.

半角模型；横向延伸；动态延伸；纵向延伸

一、缘从何起

近年来，在初中数学的几何领域中，基本图形的教学与渗透越来越受到广大数学教师的关注.唐芬老师的文章《半角模型的纵横迁移》通过对半角模型向纵、横两个方向进行了延伸拓展的探究，给笔者留下了深刻的印象.文章所涉及的模型由特殊到一般、由现象到本质，而究其根源，无不从最初始的正方形半角模型演变而来.因此，这一类题的根源都是正方形半角模型，只要把这一模型完全理解和参悟，那么，相信一定能达到“通一片”的效果.基于上述内容，笔者收集并整理了近两年来的半角模型中考试题，对其本质联系方面进行赏析，与同仁分享.

二、模型再现

如图1，在正方形ABCD中，E，F分别是BC，CD上的点，且∠EAF=45°，连接EF.求证：EF=BE+FD.

图1

【评析】此乃最初始的正方形半角模型，所求证的结论可以通过“截长”或“补短”两种思路来解决.“截长”可以通过“作垂直法”“大角分割法”“轴对称法”等来实现，如图2所示.而“补短”也可以通过“补等线段法”“小角拼合法”“旋转法”等方法来实现，如图3所示.无论用哪种方法，都需要充分利用关键条件“∠EAF=45°”，该模型的本质特点即为：虽然点E，F在动，∠EAF也随之运动，但始终不变的就是三条线段的关系“EF=BE+FD”.因此，围绕这一本质特征，各地命题专家们命制了不少“半角模型”中考试题，接下来，就让我们一起来欣赏一下吧.

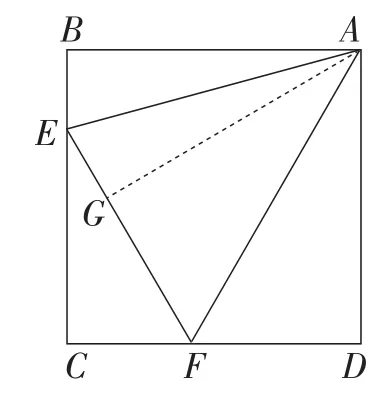
图2

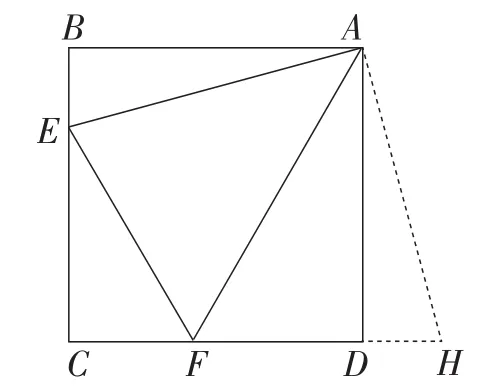
图3

三、试题赏析

在近两年的各地中考试卷中，涌现出了大量“半角模型”试题，且都涵盖了初中几何领域中的核心知识点，值得我们进行归类、整理及分析.

1.正方形向三角形的横向延伸

例1（2014年浙江·绍兴卷）（1）如图4，在正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连接EF，AG.求证：EF=FG.

（2）如图5，在等腰Rt△ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长.

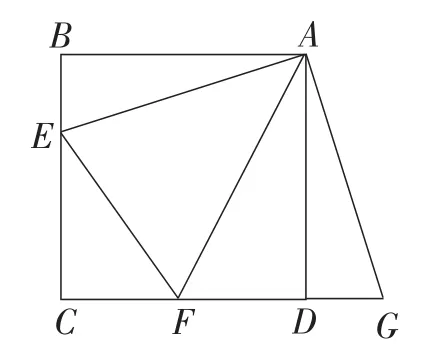
图4

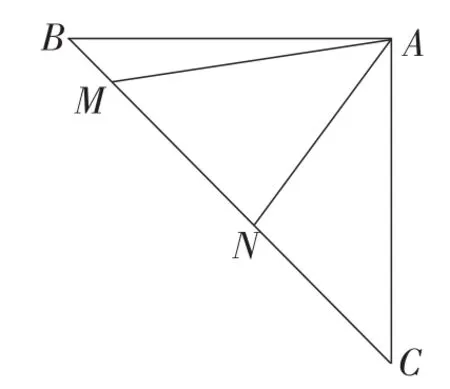
图5

【评析】该题是一道典型的正方形半角模型试题，且原本的辅助线也已呈现，放低了试题的起点.试题的两问看似证线段相等及求线段长度，但其实质仍为探究此模型中的三条典型线段的数量关系.第（1）小题的设计可以看出命题者有意给予学生思路（旋转变换思想），为解决第（2）小题做铺垫.第（2）小题也是对第（1）小题的升华，虽然图形由正方形变为三角形，但其“利用图形变换思想进行边或角的转化”的方法策略依然不变，如图6所示.试题中蕴含着直观感知、观察发现、空间想象、归纳类比等多种数学能力的考查，不失为一道好题.

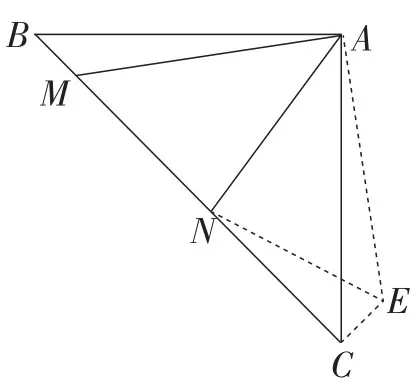
图6

2.正方形向矩形的横向延伸

例2 （2015年四川·资阳卷）如图7，在△ABC中，∠ACB=90°，AC=BC=1，E，F为线段AB上两动点，且∠ECF=45°，过点E，F分别作BC，AC的垂线相交于点M，垂足分别为点H，G.现有以下结论：① AB=；②当点E与点B重合时，；③AF+BE=EF；④MG·，其中正确结论为（ ）.

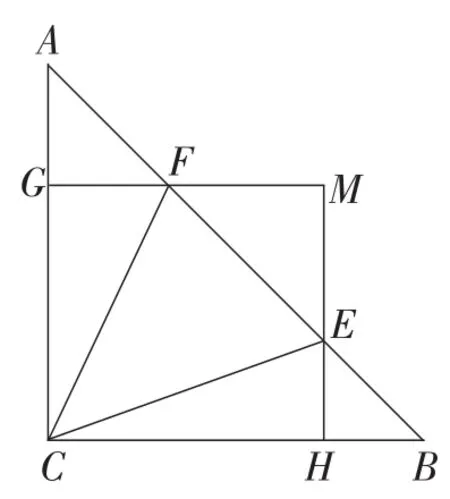
图7

（A）①②③ （B）①③④

（C）①②④ （D）①②③④

【评析】该题也是一道由正方形半角模型拓展而来的几何试题，涵盖了三角形全等、相似、特殊三角形、特殊四边形、勾股定理、中位线等核心知识，综合性极强.题目中四个结论中的结论①和结论②较为简单，对于结论③，如果去掉线段GM和HM，就成了例1中的第（2）小题了，可通过“利用图形变换思想进行边或角的转化”的方法策略探究出这三条线段之间的数量关系EF2=AF2+BE2.结论④的探究难度较大，矩形的介入需要将思维提升至“相似”的层次.先证△ACE∽△BFC，根据相似三角形的性质可得AE·BF=AC·BC=1，再根据四边形CHMG是矩形和平行线的性质，通过等量代换得到

该题四个结论的设置难度层层递进，思维要求也随之逐步增强.从图形上看，由正方形半角模型向矩形拓展之后，知识点也由全等向相似进行了深化，试题的考查功能得到加强.

3.正方形与圆的综合动态延伸

例3（2014年浙江·湖州卷）如图8，已知正方形ABCD，E是边AB的中点，点O是线段AE上的一个动点（不与点A，E重合），以点O为圆心，OB长为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连接OM，ON，BM，BN.记△MNO，△AOM，△DMN的面积分别为S1，S2，S3，则下列结论不一定成立的是（ ）.

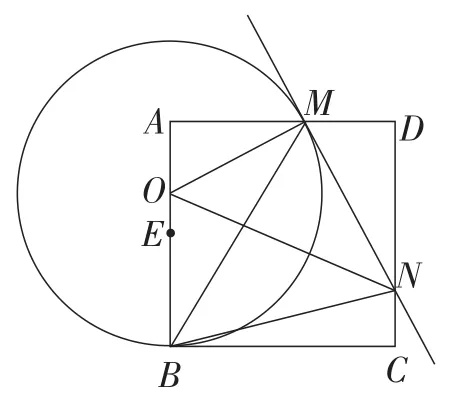
图8

（A）S1＞S2+S3（B）△AOM∽△DMN

（C）∠MBN=45° （D）MN=AM+CN

【评析】该试题作为动态几何问题，融入了正方形半角模型，可谓是在基本图形中，点线双动带来变量和不变量，让学生体验在运动变化过程中将问题从定性和定量两个方面进行探究.主要涉及的知识点有：切线性质、正方形的性质、相似三角形的判定和性质、勾股定理、旋转变换等，综合性很强.对学生思维能力要求较高，具备较强的探究能力、丰富的想象能力及综合分析问题的能力.有效地考查了学生观察、探究、猜测、推理、运算等能力.问题的难点在于如何在变化中寻找不变的量，即∠MBN始终等于45°.半角模型中的45°角是直接给出，而该题需证明出∠MBN=45°才能继续做探究.由此可见，基本图形的掌握不仅仅只是停留在顺向思维的层面，需要顺逆双向思维的灵活贯通.结合此题，过点B作BP⊥MN于点P为解决该题难点的关键一步，如图9所示，进而利用“轴对称法”解决问题.通过对该题的分析，可以发现，正方形半角模型出现的范围很广，可能与其他知识背景相结合，也可以以动态的形式呈现，但不管以怎样的形态呈现，“利用图形变换思想进行边或角的转化”的方法策略得出三条关键线段之间的数量关系，是解决这类问题的关键所在.

4.正方形自身的纵向延伸

图9

例4 （2015年广东·深圳卷）如图10，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于点G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④在以上4个结论中，正确的有（ ）.

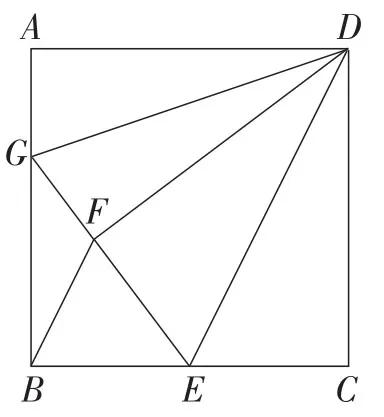
图10

（A）1个 （B）2个

（C）3个 （D）4个

【评析】该试题从图形上看较简洁，只是在初始正方形半角模型的基础上增加了两条线段.图形的形成也只是通过一次轴对称变换加延长和连接所成.结论①是对基本图形的一次基础考查和验证的过程，结论②则需通过该模型的本质特征“AG+CE=GE”，利用方程思想来解决，结论③通过之前的计算进行三角形形状的判定即可，结论④同样可以根据之前的计算求得结果.由此可见，该题的关键是结论②的证明，需要充分利用半角模型的本质特征，即三条线段之间的数量关系，最终得以解决.

例5 （2014年山东·菏泽卷）已知：如图11，正方形ABCD，BM，DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MN.

（1）若正方形的边长为a，求BM·DN的值；

（2）若以BM，DN，MN为三边围成三角形，试猜想三角形的形状，并证明你的结论.

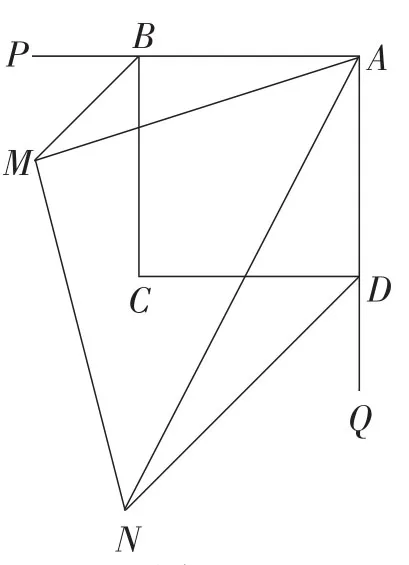
图11

【评析】在原半角模型的基础上增加条件或改变条件即构成了“正方形自身的纵向延伸”.该试题就在原半角模型的基础上增加了“两条外角平分线”的条件，思维层次也随之提升，然而，学生如能抓住原半角模型的本质，深知其中所蕴含的边角关系，解决此题也并非难事.第（1）小题可以通过三角形相似的证明轻松得出结论.第（2）小题仍然可以“利用图形变换思想进行边或角的转化”的方法策略，当然，图形变换思想可以是旋转变换，也可以是轴对称变换，于是就能想到两种方法：方法1，可以利用旋转变换把所要研究的三条线段转化到同一个三角形中，进而解决问题，如图12所示；方法2可以利用轴对称变换将这三条线段转化到同一个三角形中，如图13所示.以上两种方法形变质不变，虽然辅助线的添加不同，但其方法策略是一致的，均为“利用图形变换思想进行边或角的转化”，此为该题思维的“脚手架”，掌握了这一策略也就掌握了这一类题.

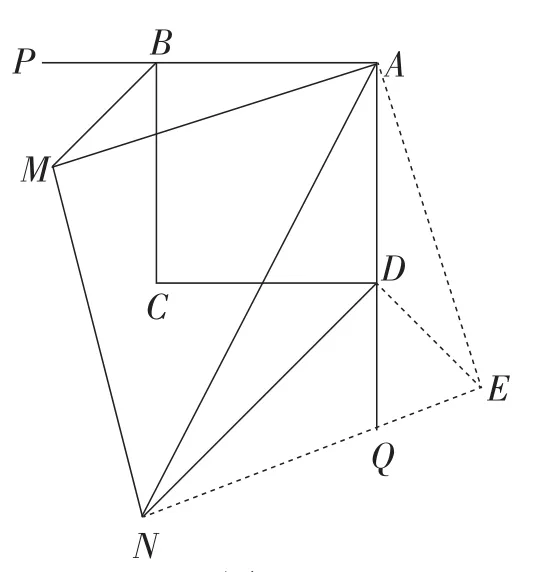
图12

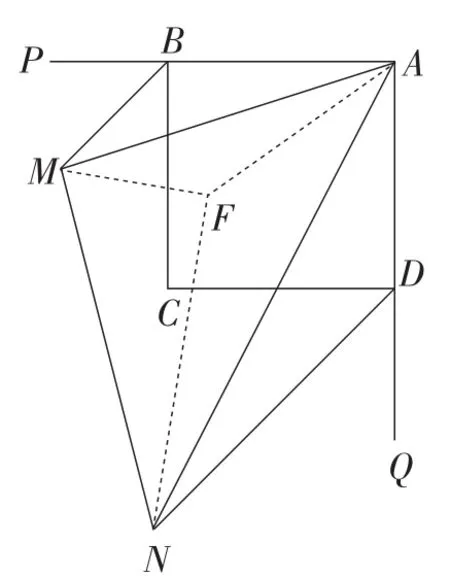
图13

四、赏题启示

1.提炼基本模型，抓住思维“生长点”

《义务教育数学课程标准（2011年版）》特别强调：数学活动经验的积累是提高学生数学素养的重要标志.帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果.以上中考试题，均由“半角模型”演变而来，虽然图形、条件、问题都有所变化，但每道题的解题策略类似，都为利用图形变换思想进行边或角的转化，进而使得要探究的三条线段存在显而易见的关联.教师需要在平时的教学中，充分挖掘例、习题的内在价值，特别是蕴含基本模型的例、习题，要引导学生去发现并归纳基本模型中的特殊边角关系，即抓住思维“生长点”，为解决问题搭建思维“脚手架”.

2.拓展基本模型，寻求思维“延伸点”

基本模型经过提炼与归纳之后，需要对该基本模型的发展和应用进行进一步的深入探究，即寻求思维“延伸点”.文中的正方形“半角模型”，在经过教师的引导让学生提炼和总结后，教师如果能够及时对该模型进行拓展延伸，相信学生的思维层次不仅仅只是停留在抓住思维“生长点”的层次，而应是寻求思维“延伸点”的层次.让学生在拓展基本模型的过程中，体悟解题通法，从而做到化题为型、凝题成链、结题成网，真正实现“解一题，会一类，通一片”.

3.关注模型教学，追求思维“发散点”

从近几年的各地中考试题中，不难发现，渗透基本模型的试题逐年增加，在各类公开课和展示课中，也经常有“基本模型教学”的身影.由此可见，如今的初中数学几何教学，“基本模型”教学已越来越被重视.数学试题千变万化，而基本模型又万变不离其宗，目前已被广泛应用的“基本模型”还不是很多，在这块领域，有很大的提升空间.基于此，教师应多研究试题，善于挖掘并提炼新型的“基本模型”，甚至可以引导学生自主去发现并提炼“基本模型”，追求思维“发散点”，最终实现“思维品质”的提升，相信这是初中数学几何教学更高层次的体现.

［1］唐芬.半角模型的纵横迁移［J］.中学数学教学参考（中旬），2014（5）：42-44.

［2］沈岳夫.对2014年浙江省绍兴市中考第23题的研究与拓展［J］.中国数学教育（初中版），2015（5）：20-23.

［3］白雪峰，王敬如.追根溯源 返璞归真：一道中考试题的证明和拓展［J］.中国数学教育（初中版），2015（5）：27-31.

［4］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

2017—01—12

姜晓翔（1978—），男，中学高级教师，主要从事课堂教学、解题教学研究.