破译黄金密码 感受数学之美——“黄金分割与数学”教学设计与分析

谢立光

（江西省赣县教育局教研室）

破译黄金密码 感受数学之美
——“黄金分割与数学”教学设计与分析

谢立光

（江西省赣县教育局教研室）

激发学生的数学学习兴趣，引导学生发现生活中蕴含的数学美，使学生在学习掌握知识的同时，深切的感受到数学的文化价值，是数学教师的重要职责.本课以探究黄金分割的教学为切入点，通过合理假设、归纳猜想、分析证明，从感性、理性两个层面去学习、认识、运用黄金分割，激发学生学习数学的兴趣，使学生从“数”与“形”的角度感受数学之美、生活之美，引导学生去发现美、探索美、欣赏美、创造美，旨在引导学生因发现数学之美而爱上数学.

黄金分割；教学设计；数学之美

在数学史上，“黄金分割”与“勾股定理”被称为“几何双宝”，黄金分割这个数字一直被后人奉为科学和美学的金科玉律.但是，黄金分割概念的理解和黄金分割点的作法对学生来说有一定难度.鉴于黄金分割的特殊性，笔者采用了以学生寻找、感悟、体会美的方式来串联各个教学环节，每个教学环节中都安排学生探索黄金分割的不同侧面，从而介绍黄金分割的有关知识点.以下为教学设计与分析.

一、教学任务分析

1.教材分析

本节课是北师大版《义务教育教科书·数学》八年级下册第四章第二节的内容，主要是黄金分割的概念、作图与简单应用，属于“图形与几何”的领域.本节课是在学生学习了三角形、四边形、二次根式和一元二次方程的基础上安排的.

黄金分割不仅是线段的比的延续，还与几何中的三角形、矩形、五角星，代数中的数列、极限，有着千丝万缕的联系.探究黄金分割，不仅可以进一步培养学生观察、分析、归纳、概括的能力，更能促进审美意识的发展.因此，黄金分割是整个初中数学教材中与生活联系最密切、最富有美感的内容.

2.学情分析

学生已有比和比例、勾股定理、二次根式、一元二次方程等知识基础，学生理解黄金分割的意义并不难，但黄金分割点的作法对学生来说有一定的困难，需要从构建直角三角形中找到作图思路，理解作图方法与步骤.通过设计丰富的数学活动，理解、掌握黄金分割的有关知识，挖掘其在实际生活中的运用，引导学生发现美、欣赏美、创造美.

3.教学目标

（1）了解黄金比、黄金分割的概念，会作任意线段的黄金分割点；

（2）知道黄金矩形，会利用黄金分割知识解决简单的实际问题；

（3）通过现实情境与素材了解黄金分割的应用，体会数形结合思想，感悟数学之美；

（4）通过小组合作学习，体会在解决问题的过程中与他人合作的重要性，从而培养学生的团结协作精神.

4.教学重点、难点

教学重点：理解黄金分割的意义、并能作出已知线段的黄金分割点.

教学难点：会利用线段的黄金分割解决简单的实际问题.

5.教学策略分析

本节课教学内容与现实生活联系密切，在教学中借助丰富的生活情境，采用直观演示法、引导发现法和小组讨论等学习方式，让学生在做中学、学中做，同时揭示数学的文化价值，提升学生的审美观，培养学生的应用意识和创新意识.

6.教学准备

flash课件、矩形纸条.

二、教学流程

本节课教学流程设计如图1所示.

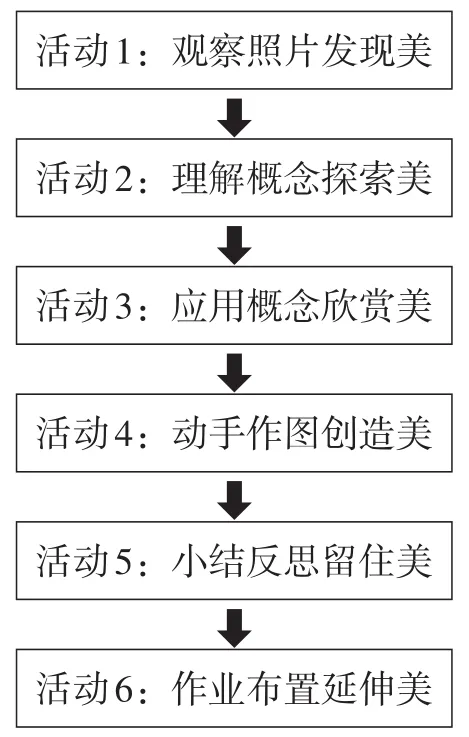
图1

三、教学过程设计与分析

活动1：观察照片发现美

（1）如图2与图3的两张照片，哪张构图更美？

图2

图3

（2）如图4与图5，芭蕾舞演员做相同的动作，不踮脚尖和踮脚尖，哪个更美？

图4

图5

美是一种感觉，为什么刚才几乎所有的学生对美的认识都是一致的？难道这些给人美感的图片中蕴藏着某个规律？

教学分析：情境引入提供两组学生日常生活中的图片，在对比过程中，使学生对美产生切实的感受，教师通过设疑提问，激发学生的好奇心和求知欲，感知发现生活中的黄金分割，感受数学与生活的密切联系，从而引入新课.

活动2：理解概念探索美

古希腊数学家欧多克索斯曾提出：能否将一条线段分成不相等的两部分，使较长线段与原线段的比等于较短线段与较长线段的比（即黄金分割问题）？

如图6，点C把线段AB分成两条线段AC和BC，AC＞BC，思考：

（1）是否存在这样的点C，使较长线段与原线段的比等于较短线段与较长线段的比？

（2）如果存在，较长线段为多长？

（3）如果存在，这样的点C有几个？

图6

用方程的思想探究黄金分割问题.

提示：设AB=1，较长线段AC的长为x，则较短线段CB的长为_______.

根据学生的探究结果，我们可以归纳出黄金分割的定义.

注意：一条线段有2个黄金分割点.

黄金分割最早是古希腊著名数学家毕达哥拉斯于公元前六世纪发现的.一般用希腊字母φ表示这个值，即φ≈0.618.古往今来，这个数字一直被后人奉为科学和美学的金科玉律.具体请学生见学案阅读材料.

教学分析：为了突破黄金分割的定义这个难点，让学生先猜测，然后教师给出肯定的结论，通过假设线段比存在的情况下构造方程模型，让学生在解一元二次方程的过程中，增强对比例式和比值这两个属性及其关系的理解.为探究黄金分割比提供理论依据，从而帮助学生深挖概念，把握规律，帮助学生更深刻地理解黄金分割的定义.通过用数学语言和符号来表述黄金分割，有效地实现了图形语言与符号语言的转化，培养了学生的符号意识.

活动3：应用概念欣赏美

（1）摄影与黄金分割（图7与图8）.

图7

图8

（2）人体与黄金分割（图9与图10）.

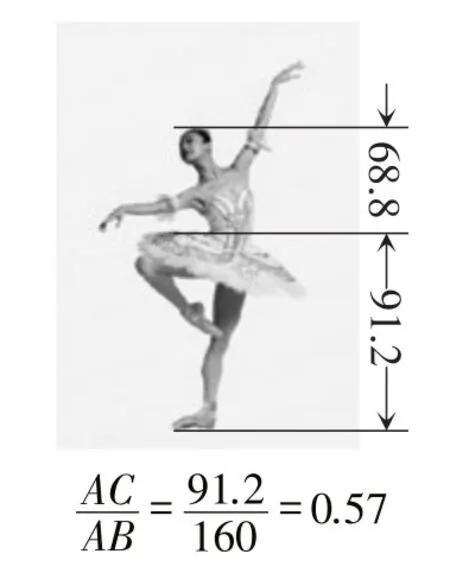
图9

图10

在人体下半身与身高的比例上，越接近0.618，越给人美感.遗憾的是，即使是身体修长的芭蕾舞演员也达不到如此的完美.

（3）美术与黄金分割.

如图11，世界名画《蒙娜丽莎》之所以那么优雅、美丽，也得益于黄金分割，无论是画面整体中的矩形还是局部的矩形都满足：

图11

图12

（4）建筑与黄金分割.

例1 如图13，如果把巴台农神庙的轮廓抽象为矩形ABCD，以矩形ABCD的宽为边在其内部作正方形AEFD，那么我们可以惊奇的发现

图13

（1）点E是AB的黄金分割点吗？

（2）矩形ABCD的宽与长的比是黄金比吗？

（3）矩形EFCB是否也是黄金矩形？

教学分析：为了与开头的情境导入相呼应，通过提出的问题，让学生在现实情境中感知新知的应用价值，让学生了解黄金分割在摄影、人体、美术中的应用价值的同时，进一步凸显黄金分割的作用和价值，也了解黄金矩形，为讲解黄金分割在建筑中的应用做铺垫.将黄金分割的意义从一维图形扩展到二维图形，同时通过巴台农神庙展示黄金分割的历史文化价值.

活动4：动手作图创造美

例2 如图14，已知线段AB，按照如下方法作图.

（2）连接AD，在DA上截取DE=DB；

（3）在AB上截取AC=AE.

根据上述作图方法（如图15），回答下列问题：

（1）如果设AB=2，则BD=_____，AD=____，AC=____，BC=_____.

试问：点C是线段AB的黄金分割点吗？

（2）如果AB=a，点C是线段AB的黄金分割点吗？

图14

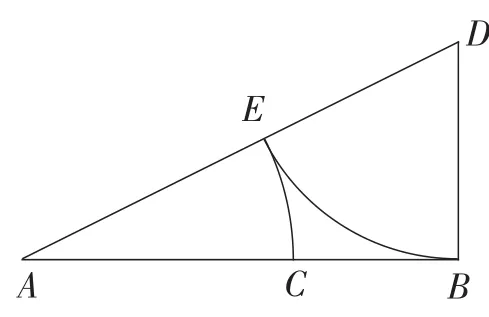
图15

试一试：如图16，用宽度为2的矩形纸片折黄金矩形.

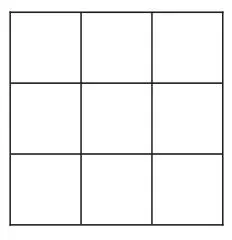
图16

活动5：小结反思留住美

请学生回忆、归纳一下收获与感受.

教学分析：学生先小组总结，再派代表发言来谈感受.不仅训练学生概括、归纳知识的能力，使知识系统化、条理化，培养学生的归纳、反思意识.

活动6：布置作业延伸美

必做题：

1.如图17，主持人主持节目时，站在舞台的黄金分割点处最自然得体，已知舞台AB长为20 m，则主持人乐乐应站在离点A_______处，如果她向点B再走______，也处在自然得体的位置.

图17

2.把一根长4 m的铁丝弯成一个矩形框，使它的宽与长的比为黄金比，则这个矩形框的面积是______.

选做题：

结合下面的阅读材料“养生学中的黄金分割”，为父母提出几个养生建议.

环境气温：使用空调时室内温度调到22℃ ～24℃，在这个气温下生活最舒适.因为人的正常体温为36℃～37℃，这个体温与0.618的乘积恰好是22.4℃～22.8℃，而且在这一环境温度中，人体的生理功能、生活节奏等新陈代谢水平处于最佳状态.

饮食：一餐主食中要有六成粗粮和四成细粮的搭配进食，有益于肠胃的消化与吸收，避免肠胃病.

生活作息：24小时中，为了提高工作效率，工作时间与休息与睡眠的比例为4∶6.

运动和静养：“四分动，六分静”是最佳的保建之道.

延缓衰老：生理上的抗衰为四，心理上的抗衰为六，充分调动与合理协调心理和生理两方面的力量，可以达到最好的延年益寿的效果.

教学分析：为了提高学习的效率，把问题设计成填空题的形式，有层次、有梯度，易于被学生接受，关注了不同层次的学生.选做题是一道温馨家庭作业，不仅可以让学生活用数学，还可以拉近父母与子女之间的感情.

四、教学感悟

可以说，精巧的教学设计、有趣的课堂活动，以及黄金分割本身所独有的数学魅力紧紧地抓住了学生的心.本节课，学生亲历了发现美、探索美、欣赏美、延伸美、留住美、创造美的过程，从中不仅感受到了探究问题的艰辛，更体验到了数学思考的乐趣和成功的喜悦.这是一节让教师和学生都乐在其中的课，教师和学生一起一点一点地破译黄金分割的密码，感受数学之美！

在数学教学中，教师要积极创设条件，充分调动学生学而不厌的主观能动性，让学生有意识、有兴趣、有责任地参与教学活动，才能较好地解决知识上的难点问题，使学生在学习中积极主动地建构自己的知识，真正成为教学中的“主体”.

让灵动的课堂充满数学之美！

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］罗增儒，李文明.数学教学论［M］.西安：陕西师范大学出版社，2010.

2017—02—01

谢立光（1969—），男，中学高级教师，主要从事中学数学教育与教学、教育科研管理、全国教育调研研究.