基于差分进化的二级圆柱齿轮减速器优化设计

盛志杰

（建东职业技术学院，江苏常州213022）

基于差分进化的二级圆柱齿轮减速器优化设计

盛志杰

（建东职业技术学院，江苏常州213022）

文章首先简述了二级圆柱齿轮减速器的数学模型，然后提出了基于差分进化的二级圆柱齿轮减速器优化方案，并与传统方案进行对比，对比结果显示差分进化法有利于减小减速机的尺寸，降低制造成本，对拓展应用市场的范围具有积极意义。

二级圆柱齿轮减速器；差分进化；数学模型

二级圆柱齿轮减速器广泛应用于工矿企业、交通运输部门和建筑行业。由于传统的优化设计方法采用手动迭代或计算机语言，优化模型具有高维、线性非凸、多约束的特点。其计算量大且相对繁琐，因此优化结果不理想。通常安装空间将受到较小场合的限制，因此为了满足其承载能力，使用寿命和可靠性的条件，在其体积和结构尺寸的前提下应采用优化设计。

1 二级圆柱齿轮减速器数学模型构建

如图1所示，二级圆柱齿轮减速器的输入功率设置为6.2kW，高速轴转速为1450r/min，总传动比为31.5，齿宽因素为0.4。由图1可知，小齿轮45号钢调质硬度介于228-255HB之间，而大齿轮45号钢正火硬度介于187-207HB之间。二级圆柱齿轮减速器的工作年限在10年以上。

图1 二级圆柱齿轮减速器结构图

（1）目标函数的建立。目标函数：F（X）=a=a1+a2=［mn1z1（1+i1）+mn2z3（1+i2）］/（2cosβ）。改目标函数表示齿轮减速器的最小体积，总中心距最小，意为结构最紧凑、质量最轻。其中“a”表示总中心距，“a1”表示高速级中心距，“a2”表示低速级中心距，“mn1”表示高速级齿轮法面模数，“mn2”表示低速级齿轮法面模数，“i1”表示高速级传动比，“i2”表示低速级传动比，“z1”表示高速级小齿轮齿数，“z3”表示低速级小齿轮齿数，“β”表示齿轮螺旋角。

（2）设计变量的确立。设计变量：［mn1，mn2，z1，z3，i1，β］T=［x1，x2，x3，x4，x5，x6］T。其中mn1，mn2，z1，z3，i1，β等参数均参与总中心距a的计算。

（3）约束条件的确认。根据渐开线齿轮承载能力的计算法则，齿轮必须同时符合以下两个条件：①齿根弯曲疲劳强度条件；②齿面接触疲劳强度条件。具体内容如下：首先，确认设计变量的上下界限：取：14≤z1≤22；16≤z3≤22；2 mm≤mn1≤5 mm，3.5mm≤mn2≤6 mm，5.8≤i1≤7，8°≤β≤15°（需换算成弧度）。对应6个不等式约束条件：2≤x1≤5，3.5≤x2≤6，14≤x3≤22，16≤x4≤22，5.8≤x5≤7，8≤x6≤15。以上不等式表明，传动要保持平衡，轴向力不宜过大，适应短期过载，高速级大齿轮与低速级大齿轮具有基本一致的浸油深度，轴齿轮分度圆尺寸适中。其次，确认齿面弯曲强度条件：

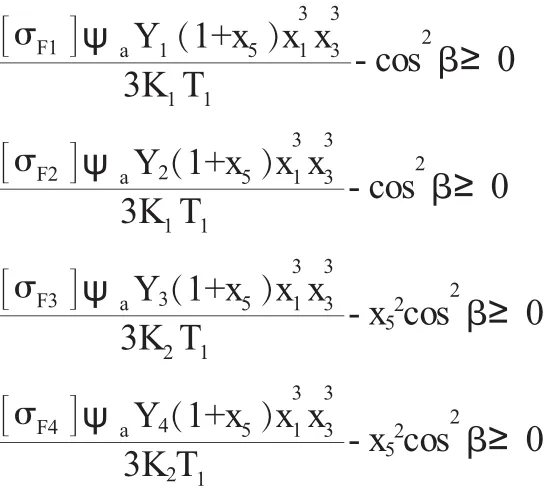
其中“［σF1］”齿轮1的许用弯曲应力；“［σF2］”表示齿轮2的许用弯曲应力；“［σF3］”表示齿轮3的许用弯曲应力；“［σF4］”表示齿轮4的许用弯曲应力。“Y1”表示齿轮1的齿形系数；“Y2”表示齿轮2的齿形系数；“Y3”表示齿轮3的齿形系数；“Y4”表示齿轮4的齿形系数。然后，确认齿面接触强度条件。高速级齿面接触强度条件：

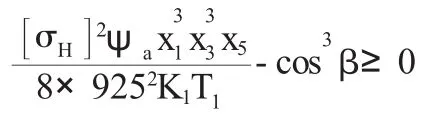
低速级齿面接触强度条件：

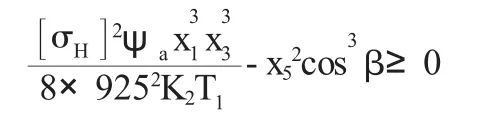
其中“［σH］”表示许用接触应力；“T1”表示高速Ⅰ轴和中间轴的转矩；“T2”表示高速Ⅱ轴和中间轴的转矩。T2=T1i1。“K1”表示高速级载荷因数；“K2”表示低速级载荷因数。最后，确认几何约束条件：a2-E-De2/2≥0。x2x4（i+x5）-2cosβ（E+x1）x5-x1x3x52≥0。其中“E”表示低速轴轴线与高速级大齿轮齿顶圆之间的距离。“De2”表示高速级大齿轮的齿顶圆直径。

2 基于差分进化的二级圆柱齿轮减速器优化

（1）差分进化。①变异操作：从群体中随机选择一个个体作为基本向量，将另外两个不同个体作为差向量，获取突变的个体。②交叉操作：交叉操作是在变异产生的第一个个体和种群中的第一个个体之间进行，交叉操作得到试验个体。③选择操作：DE的选择是一对一的选择，其在实验载体和原始群体的个体之间进行，选择的原则是更好地适应个体到下一代。

图2 ADE迭代曲线

（2）参数优化。如图2所示，采用ADE算法，取种群规模NP=100，交叉概率CR=0.9，最大进化代数Gmax=1000，缩放因子F=2e［1-Gmax/（Gmax+1-G）］。对总中心距a的最小值进行优化。

优化参数：X=［mn1，mn2，z1，z3，i1，β］T=［x1，x2，x3，z4，x5，x6］T=［2.5，4，15，17，7，11°56′25″］；a=a1+a2=［mn1z1（1+i1）+mn2z3（1+i2）］/（2cosβ）=273.1110mm，圆整后取300mm。

（3）ADE优化设计与传统设计对比。

传统设计：mn1=3mm，mn2=5mm；z1=19，z3=17，i1=6.3；β=11. 0222°；f=470.15；圆整=500mm。

优化设计：mn1=2.5mm，mn2=4mm；z1=15，z3=17，i1=7；β=11. 9403°；f=273.1110；圆整=300mm。

3 结语

在保证齿轮承载能力的前提下，优化结构参数。结果表明，优化设计方法大大减小了减速机的尺寸，降低了制造成本，扩大了应用市场。差分演化算法使用动态缩放因子来降低用户参与的程度。考虑收敛速度，避免获得局部最优解和全局最优解的能力。

［1］陈添喆.基于圆柱齿轮设计中齿数优化的探索与分析［J］.装备机械，2014，8（3）：800-802.

［2］高妍，王三民，袁茹.基于渐开线齿廓存在域的直齿圆柱齿轮直接设计方法研究［J］.机械制造，2013，6（9）：194-196.

［3］叶洪涛，罗飞，许玉格.解决多目标优化问题的差分进化算法研究进展（英文）［J］.控制理论与应用，2013，6（7）.

［4］赵炜，马晓雪，宁方立.渐开线圆柱齿轮传动参数化设计系统的研究与开发［J］.机械制造，2013，6（3）：840-843.

［5］潘全科，王凌，高亮.基于差分进化与块结构邻域的作业车间调度优化［J］.机械工程学报，2010，3（22）：842-845.

Optimum Design of Secondary Cylindrical Gear Reducer Based on Differential Evolution

SHENG Zhi-jie
（Jiandong Vocational and Technical College，Changzhou，Jiangsu 213022，China）

In this paper，the mathematical model of the two-stage cylindrical gear reducer is briefly introduced.Then，the optimization scheme of the secondary cylindrical gear reducer based on differential evolution is proposed and compared with the traditional scheme.The results show that the differential evolution method Reducer size，reduce manufacturing costs，to expand the scope of the application market has a positive significance.

secondary cylindrical gear reducer；differential evolution；mathematical model

TH132.46

A

2095-980X（2017）03-0081-02

2017-02-08

盛志杰（1967-），男，江苏常州人，教师，工程师，主要研究方向：高职机械教育。