RGB Based Multiple Share Creation in Visual Cryptography with Aid of Elliptic Curve Cryptography

K. Shankar＊, P. Eswaran

1 Research Scholar, Department of Computer Science and Engineering, Alagappa University, Karaikudi – 630003, Tamil Nadu, India

2 Assistant Professor, Department of Computer Science and Engineering, Alagappa University, Karaikudi – 630003, Tamil Nadu, India

* The corresponding author, email: shankarcrypto@gmail.com

I. INTRODUCTION

Nowadays it has become a fashion to transmit multimedia data by means of the all-pervasive Internet. With the advent of electronic commerce, it has become extremely essential to tackle the sensitive issue of affording data security, especially in the ever-zooming open network environment of the modern era. The encrypting technologies of time-honored cryptography are generally employed extensively to shelter data safety. [1] A universal technique for data concealing has been the employment of the watermarking method. And in this regard, credit goes to Shamir for launching a well-acclaimed method for secret sharing which is known by the name cryptography technique. In addition, Naor and Shamir have gone further ahead and vigorously advocated the concept of visual cryptography for the purpose of sharing images. [2] A new-fangled brand of secret sharing scheme is given the pet name visual secret sharing (VSS) scheme.VSS is an innovative technique in which the shared images such as printed text, handwritten notes, pictures, and the like are perceptible by k or more participants by amassing their transparencies by means of an overhead projector. [3] In Visual cryptography, a secret binary image is programmed into n shares of arbitrary binary prototypes. It is possible to decode the secret image visually by superimposing a qualified subset of transparencies.Nevertheless no secret data can be acquired from the superposition of an illegal subset [4].Moni Naor and Adi Shamir have taken pains to exhibit the visual secret sharing scheme,in which an image is split up into n shares with the result that only a person having all n shares is capable of decrypting the image and the absence of even a single share out of the n shares will land the person facing a waterloo in exposing any data on the original image.Each and every share is printed on a distinct transparency, and decryption is carried out by means of superimposing the shares. Only when all n shares are superimposed, it enables the original image to materialize [5]. As far as secret sharing is concerned, it is observed that casual appearance shares when they are integrated are capable of reinstating the secret. On the other hand, in recursive secret sharing, the shares themselves have components delineated at mediocre zones. The combination of the arbitrary bits in the shares is performed appropriately by full utilization of d-sequences or matching random sequences. [6] In the event of the two shares being overlaid together, it is observed that two black sub-pixels appear if p is black. On the other hand, a solitary black sub-pixel and solitary white sub-pixel are found to appear if p is white. Thus, we are able to distinguish whether p is black or white,in accordance with the distinction between the two types of restructured pixels. [7] It is simply impossible to attain any con fidential data by just glancing at the groups of pixels in each share. If a pixel is white, the superposition of the two shares invariably ushers in a solitary black and a solitary white sub pixel, irrespective of the column of sub pixel pair selected in the course of encoding .[8] Visual Cryptography, while employed in copyright safety ensures decision of legal ownership, dispensing with the use of the original image. Moreover,the host image does not change in the course of the embedding procedure. [9] In the conservative Visual Cryptographic scheme, the shares are stretched in dimension in relation to the size of the con fidential image. This has the effect of enhancing the space essential to amass the superior bandwidth to send out the shares.[10] In the case of augmenting the quality of the restored image, VCS-XOR frequently offers several merits on pixel development and contrast qualities when compared to the VCS-OR. It is crystal clear that the deciphering techniques have emerged as more intricate and challenging during the course of deciphering a large number of shares and in this connection, the XOR based VCS has established itself as the most realistic in respect of the (2;n) case. [11] A common method to execute comprehensive visual cryptography schemes uses hyper graph colorings. And this method is capable of ushering in the (k; k)-threshold EVCS which is optimal in relation to the pixel development. [12]

II. RELATED WORKS

In 2014, Hao-KuanTso et al. [13] have been credited with proposing the innovative technique viz. Friendly Medical Image Sharing Scheme by using the random grids. In this technique, the random grids are employed to build two insignificant shares. Thereafter,a friendly model is overlaid on the shares in such a manner that the users are capable of dealing with them and recognizing them effortlessly. It is pertinent to note that it is not possible for anyone to access the data on the patients’ images by just scrutinizing the outward appearance of the shares.

In 2013, Pandey et al. [14] have proficiently put forward the Visual Cryptography Schemes by means of Compressed Random Shares. In this technique, the visual cryptography scheme is able to usher in n number of transparent shares with condensed dimension and supports a diversity of image designs in addition to offering an integrated approach for binary, Gray and color image visual cryptography by preserving the visual excellence and pixel growth.

In 2012, R.KalaiSelvi et al. [15] have pro-pounded the method for Crypto System based Authentication using CSTA in Grid is used.In this method, the Cyclic Shift Transposition Algorithm (CSTA) is used to send the encrypted message as symbols and only the receiver receives the encrypted message which was decrypted by their private key for retaining the original message.

In 2011, Rahnamuhammed et al. [16] gets the bouquets for launching the Visual Cryptographic Biometric Template by means of the random permutation. This technique enables the encryption of visual data in such a manner that decryption can be carried out by employing the human visual system. It is found that it has enhanced the safety of visual cryptography by scrambling the image by means of random permutation.

In 2011, Constantinpopescu et al. [17] have propounded the method for A Secure E-Cash Transfer System based on the Elliptic Curve Discrete Logarithm Problem. In this method,the Elliptic Curve Discrete Logarithm was used to send the secure encrypted message with their public key and receives the encrypted message which is retained by their private key.

III. PROPOSED METHODOLOGY

The proposed visual cryptography method is used to send the image to the receiver as securely and con fidentially. The image is transferred as shares and all shares are stacked together to get back the original image. The proposed method is used to create the shares from their pixel values. The pixel values (Pv) of the color image (RGB image) are extracted from the original image and represent as matrix(P*Q). The extracted pixels values are used to create the multiple shares (share1, share2…share n) and the shares are divided into blocks.The blocks of the shares are encrypted by using the elliptical curve cryptography method and the encrypted image is decrypted by using the decryption of the ECC method. Finally the output image is compared with the original image for evaluating their performance by us- ing the peak signal noise ratio (PSNR) value,Mean square error(MSE) and correlation co efficient(CC)

3.1 Block diagram

Figure 1 shows the block diagram of the proposed method of the visual cryptography and its each block are explained in the following.

The pixel values of the secret color image(original image) is extracted and take as RGB pixel values and these values are separately indicated as matrix Rm,Gm,and Bmand the size of the matrix is the same size of the original image size (P*Q)The original pixel values of the image is

Where, pixel is the total values of the Rm,Gm and Bm. (P*Q) is the size of the original image size.

3.2.1 Share creation

Each original pixel of the secret image is appeared in ‘n’ modified versions called shares.Each share is a collection of sub-pixels of the RGB image. Each R, G, B shares are based on the pixel values of the RGB image. The share for RGB is separately indicated as Rs, Gs and Bsand indicated as

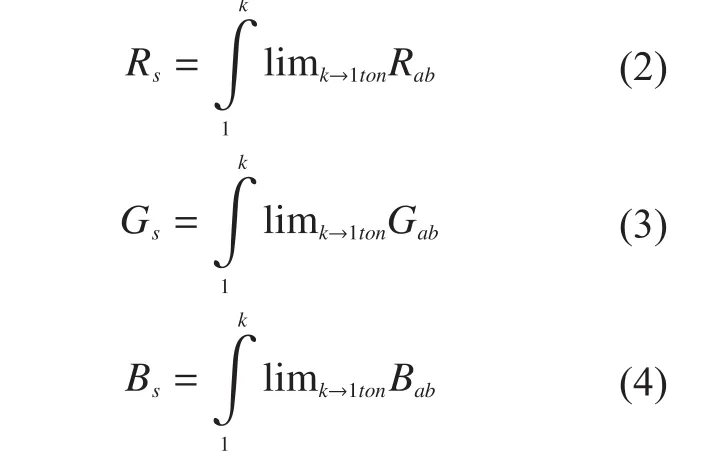
Fig.1 Block diagram of proposed method

Where, a and b are the positions in matrix,Rs,Gsand Bsare the shares of the RGB,Rab,Gaband Babare components of the image pixel. The R, G and B band pixel values are extracted from the original image and take as the separate matrix.

The shares are created based on the splitting the image into various regions. The secret sharing scheme is to encrypt a secret image into n meaningless share images. It cannot leak any information about the original image unless all the shares are obtained. Shares are obtained from the original secret image Before the encryption, first it isfinding the number of shares(n) to be generated. The user can give any value for n. Before separating the shares,the basic matrices are first constructed based upon the number of shares to be created. A random Key is generated based on block size of the secret image. Usually the block size will be 4 x 4 or 8 x 8.

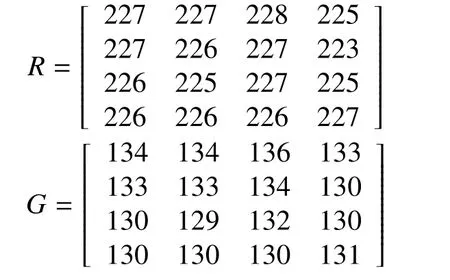
The numbers of shares are created based on the number of basic matrices if the number of shares is 2S,where S is the number of basic matrices and the S is greater than or equal to 2(S＞=2). The basic matrices are obtained by dividing each and every pixel value in R,G and B by S. For example, let the pixel value in R is 123, S is 2. 123/ 2= 61.5. So the corresponding pixel value in thefirst and second basic matrix is 42 and the third basic matrix is 43.Therefore 61+62 = 123. If S=3, then the number of shares to be produced are 22= 4.Then, the shares can be constructed by XOR-ing basic matrices on different combination.

Here, the number of basics matrices is 2 and number of shares is 4.The basic matrices construct from the pixel value of the R, G, and B divide by two. For example,

Let generate the key matrix Kmrandomly.

After that, the basic matrices are created above mentioned method and they are denoted as Rb1and Rb2

Before share creation, the following operation is performed with the Rb1and Rb2matrices.

The red band shares are created by using the XOR operation with the basic matrices and the key matrices.

From that above process apply other two pixel values of the green (GS1, GS2, GS3,GS4,Km) and blue(BS1, BS2, BS3, BS4, Km) bands used for creating the multiple shares.

Shares Reconstruction process

In the share reconstruction process multiple shares are stacked together to get the original image. That means

After shares are reconstructed and then the encryption and decryption method based on ECC method applied on each color bands of the reconstructed shares. The each color band images are divided into blocks before the encryption and decryption operation. The blocks are divided into 4*4 as block size.

From that above operations the numbers of multiple shares are created and then the encryption and decryption method based on ECC method applied on that share. The shares are divided into blocks before the encryption and decryption operation. The blocks are divided into 4*4 as block size

3.2.2 Elliptical curve cryptography

In the elliptic curve cryptography, the prime number is selected as npand private key is selected as H. Then, the Elliptic curve cubic equation is the,

Where, u and v are the constants and it is u=v=2.

If the condition X=Y is satisfied, the best point is selected for the elliptic curve. The X and Y is

Where, p (i, j) is the points of the elliptic curve.npis the prime number.

The doubling process is used to find the X and Y values.

The best point Pe(k,l) and Pfis the public key. The public key Pfis the

3.2.2.1 Encryption method

In the encryption method, each share has block and every block section is encrypted by the encryption method. The number of blocks is represented as b (i, j) where i and j are the row and column of the block of the share. In this process, the every two parts of the data in given as input for the encryption process. The data Dx(i, j) and Dy(i+1,j) and the point is

3.2.2.2 Decryption method

In the decryption process, the private key (H)is used to decrypt the message and the point C11is used decrypt the pixel point.

The Cijrepresents thefinal result of the decryption method.

From the results of the Cij, each pixel value of the image is retrieved and gets back the original image.

From the results of the Cij, each pixel value of the image is retrieved and gets back the original color bands(R, G , B) as separately.Finally to get the decrypted image as

Pseudo code for proposed method in visual cryptography

?

IV. RESULTS AND DISCUSSIONS

4.1 Experimental results

?

The following table I shows the Original image RGB bands image, and its share images.Each band has four different shares based on the multiple share creation. The shares are created based on the above mention multiple share creation method. Then, different images such as image 1(Lena), image 2(house), image 3 (peppers) and image 4(baboon) are used to generate the number of shares. Here, four shares are generated for each different original input image and shares are shown in table 1.The overall performance of the proposed method is analysed by using the peak signal noise to ratio value, mean square error and correlation coefficient value. Also different attacks are used such as salt and pepper noise,filtering noise and blurring noise to analyze the proposed method effectiveness.

In table I, various input images are employed for producing the different shares and aggregate four separate shares are made. At the point when all shares is stacked together,they will get the primary secret image. From this anyone of the shares of the multiple shares is the insignificant image which does not give any data of the primary image. The three distinctive images are demonstrated in the share images and they are indicated as R, G, and B band share images. The initial column of the image is demonstrated in the original image before the creation of the share. At that point the segments 2, 3, 4 and 5 are demonstrated the shares of the original secret image. Each one band has its own particular shares by utilizing the shares creation strategy.

In table IV, the encrypted images and its stacked images are shown in the table for different images. The stacked images are taken from the shares of the images and this stacked image is given as input to the encryption method. So the given image is encrypted clearly in the encryption process. The encrypted images are shown for the encrypted images for R,G and B with their stacked images. The encrypted image is taken after the encryption method applied on it the image and it is not given any information about the image. So the secrecy of the image is maintained without any deviation the image. Only the blurred images are getting after the image encryption method. After encryption, the decryption process is used to

retrieve the original image without any deviation of the image.

Table I Experimental results of the image

Table II Encrypted and stacked images

Table III Proposed method

The following table III is shown the proposed method with their PSNR, MSE and CC values.

In table III, the row 1, 2, 3 and 4 demonstrates the analysis results of the original images. Here, the four separate images are employed to dissect the proposed strategy.The proposed system contains the numerous share creation and encryption and decoding technique for the elliptic curve cryptography strategy. In table 2, it has the original image with its histogram image, final output image with its histogram image and its execution test qualities like PSNR, MSE and CC. The histogram image demonstrates how the image pixels are dissected in the image, furthermore gives the contrast between the original image and final image in the wake of applying the proposed strategy for analyzing the images.Through images, the proposed strategy is connected with the image and output images are indicated by their PSNR values. The PSNR value indicates the nature of the image to the output image after the proposed technique connected with it. Here, the PSNR qualities are 58.0025, 57.4297, 56.684 and 58.1438.Also the MSE values and CC values are shown in table 2.From the MSE values, it gives the original image and decrypted image differences and It should be minimum for any images. Here, the MSE values are nearly 0.1 and it gives the original image is retained in decrypted image after the proposed part.

4.2 Performance analysis

The statistical analytic research on the proposed image encryption strategy is demonstrated its unrivaled perplexity and dissemination properties which emphatically oppose measurable assaults. This is indicated by a test on the histograms of the enciphered images and on the correspondences of neighboring pixels in the decrypted image. The histograms images are properly shown the decrypted image and unique image contrasts furthermore gives how the pixels of the images are circulated in the image that are encrypted and decrypted without diminishing the image aspect.

4.2.1 Correlation coefficient (CC) factor

Correlation is often a measure of the relationship involving a couple of variables. If the a two variables are the image and its encryption,then they are usually in great correlation and also the correlation coefficient equates to one,when they are remarkably reliant(identical). If so, the particular encrypted image is equivalent to thefirst image and also the encryption process was unsuccessful in concealing the important points in the original image. If the correlation coefficient equates to zero, then this original image and its encryption are usually different, i.e. the particular encrypted image does not have any different characteristics and it’s remarkably independent of the original image. To analyze the correlation involving two adjacent pixels throughout plain-image as well as ciphered image, this process has been executed. Initially, randomly choose 1000 pairs associated with two adjacent (in horizontal, vertical, and diagonal direction) pixels from an image. Next, compute the correlation coefficient of each one set through the subsequent equations,

Where, W(p,q) is the correlation coefficient,M(p) and M (q) are the mean value of the Pland qland both values are ≠0.Pland qlare the two adjacent pixel values; Fpis the number of pairs (p,q).

4.2.2 Mean square error (MSE)

The Mean Square Error is the average square of the error in particular images and the following equation is

Where, W is the width of the original image,L is the length of the original image,p and q is the row and column value of the pixel,OI is the original image pixel and EI is the decrypted image pixel value.

4.2.3 Peak signal to noise ratio (PSNR)

The peak signal to noise ratio is defined as the ratio between the maximum possible power of the signal and the power of corrupted noise.

Where, MSE is the mean square error value of the image.

4.3 Attacks

The different types of attacks applied on the image for stealing the information of the image or blurring the image for reducing its quality of the image. The positions of the pixel values are changed in the image for finding the image without changing its image quality. The following tables are shown the attacks applied image and its encrypted images and stacked images. In table 3, the salt and pepper attack is applied on the encrypted image and the encrypted image is shown in table. The attack is changed the image information but the proposed method is retrieve the image with the minimum noise and its PSNR value is nearly 60% retrieved. So it is maximum retrieve the information with the minimum distortion.

The above table 4 is shown the proposed method with the attack applied on it and after attack is applied on the image, the proposed method is effectively retrieve the original image nearly 70% of the original image values is retrieved without affecting the image quality.The following table 5 is shown the comparison graph for the attack applied on the different images with their PSNR, MSE and CC values.It is clearly shown that the proposed method is retaining the original image with the maximum PSNR value.

The above table 5 shows the different im-ages are compared with the proposed method and attacks applied on it. The PSNR value graph is clearly shown that the proposed method is given better result and it retrieves the maximum the original image quality. Also the attacks is applied on the images for checking the image quality and compared with the proposed method values.

Table IV Attack applied

Table V Comparison for different image with attacks applied

4.4 Comparison between the proposed method and existing method

The proposed algorithm is compared with the existing algorithm which is based on Rubik’s Cube Principle (reference number.18) and the tabular column shows the results for the different images.

From the table, the PSNR value of the proposed method is higher than the existing method and mostly it is 35% to 40% improved from the exiting method. So the image quality is improved by the proposed method. In MSE value, the mean square error is minimized by the proposed method compared with the existing method. Because the MSE value shows the how the pixels are exchanged and shuf fled within the image and how it is retrieved by the method. From that, the image quality also improved and it has very low error value in proposed method. In the Correlation Co efficient value, the proposed method has the maximum CC value which is 1.It indicates that the all pixels are retrieved by the proposed method.So the image quality is improved. It is comparatively low in the existing method. In all points of view, the proposed ECC with multishare method is given the best output and it retrieves maximum value. The following table is shown the comparison graph for the proposed and existing method. It clearly indicates the proposed method gives the best result compared with the existing method.

Table VI Proposed and existing method without attack applied

The above table 7 shows the different images are compared with the existing method and the proposed method. The PSNR value graph is clearly shown that the proposed method is given better result and it retrieves the maximum the original image quality and the existing method compared with the proposed method values. From that, the proposed method is given best result.

V. CONCLUSION

In the ground-breaking technique, the multiple shares with the elliptical cryptography for visual cryptography have been found to usher in superlative performance. A plethora of illogical-shares are generated which are effectively encrypted and decrypted by means of the encryption and decryption technique in line with the elliptic curve cryptography. It is clear that the PSNR values are 58.0025, 57.4297, 56.684and 58.1438 the image excellence is preserved in spite of ambushes made on the secret image. The correlation coefficient value is the almost all the images are nearly 1 and the mean square error is the 0.103, 0.1176, 0.1454 and 0.0997.From that, the original image quality is not assorted and it is retained by using the proposed method. The correlation coefficients and histogram estimations have made it crystal clear that the encryption technique is performed on the secret image so as to preserve the con fidentiality of the image. Thus the confidentiality of the image is upheld in the long run and the reclaimed image is offered the unique image without in any way adversely in fluencing the quality of the image. In future,the performance of the peak signal to noise ratio will be improved by using the optimization technique. By using this, the image quality is also improved as well as minimizes its mean square error value.

Table VII Comparison between the proposed and existing method

Appendix

Table 1 PSNR values for all images

Table 2 MSE values for all images

?

Table 3 CC values for all images

[1] Young-Chang Hou, “Visual cryptography for color images”, Journal of Pattern Recognition,Vol.36, pp.1619 – 1629, 2003.

[2] Chang-Chou Lin, and Wen-Hsiang Tsai,”Visual cryptography for gray-level images by dithering techniques”, Elsevier journal of Pattern Recognition Letters, Vol.24, pp.349–358, 2003.

[3] ching-nung yang and Chi-SungLaih,”New Colored Visual Secret Sharing Schemes”, Journal of Designs, Codes and Cryptography, Vol.20,pp.325–335, 2000.

[4] Anusha and Subba Rao, “Visual Cryptography Schemes for Secret Image”, International Journal of Engineering Research and Technology,Vol. 1, No. 5, pp. 1-9, 2012

[5] Joshi Jesalkumari and Sedamka, “Modified Visual Cryptography Scheme for Colored Secret Image Sharing”, International Journal of Computer applications Technology and Research,Vol. 2, No. 3, pp. 350-356, 2013

[6] Kak, S. and Chatterjee, A. “On decimal sequences,” IEEE Transactions on Information Theory, IT-27:pp.647-652, 1981.

[7] Rahna. P. Muhammed, “A Secured Approach to Visual Cryptographic Biometric Template”, Journal of Network Security, Vol.2, No.3, 2011.

[8] Abhishek Parakh and Subhash Kak,”A Recursive Threshold Visual Cryptography Scheme”, Journal of Cryptography and Security, Vol.1, pp.1-8,2009.

[9] Feng Liu and ChuanKunWu,”Optimal XOR based(2,n)-Visual Cryptography Schemes”, Journal of IACR Cryptology,Vol.545,2010.

[10] Soumyahegde, and BhaskaraRao, “Visual Cryptography (VC) using Zigzag Scan Approach”,Journal of computer science engineering and technology, Vol.1, No.8, pp.456-461, 2011.

[11] Carlo Blundoa, Alfredo De Santis, and MoniNaor,”Visual cryptography for grey level images”, Journal of Information Processing Letters Vol.75, pp.255–259, 2000.

[12] Giuseppeateniese, Carloblundo, AlfredodeSantis, and DouglasR.Stinson,”Extended capabilities for visual cryptography”, Journal of Theoretical Computer Science, Vol. 250, pp.143-161, 2001.

[13] Hao-Kuan Tso, Tsung-Ming Lo, and Wei-Kuei Chen, “Friendly Medical Image Sharing Scheme”, Journal of Information Hiding and Multimedia Signal Processing, Vol.5, No.3,pp.367-378, 2014.

[14] L. N. Pandey and Neerajshukla, “Visual Cryptography Schemes using Compressed Random Shares”, Journal of Advance Research in Computer Science and Management Studies,Vol.1,-No.4,pp.62-66,2013.

[15] R.Kalai Selvi and V. Kavitha, “Crypto System based Authentication using CSTA in Grid” International Journal of Computer Applications,Vol.48, No.22, June 2012.

[16] RahnaP.Muhammed,”A Secured Approach to Visual Cryptographic Biometric Template”, Journal of Network Security, Vol.02, No.3, pp.15-17,2011.

[17] Constantin POPESCU, “A Secure E-Cash Transfer System based on the Elliptic Curve Discrete Logarithm Problem”, Journal of INFORMATICA,Vol.22, No.3, pp.395–409, 2011.

[18] Khaled Loukhaoukha, Jean-Yves Chouinard, and Abdellah Berdai, “A Secure Image Encryption Algorithm Based on Rubik’s Cube Principle”,Journal of Electrical and Computer Engineering,Vol.2012,pp.1-14,2012.