High-Performance Beamformer and Low-Complexity Detector for DF-Based Full-Duplex MIMO Relaying Networks

Feng Shu, Ye Zhou, Riqing Chen, Jin Wang, Jun Li, Branka Vucetic

1 College of Computer and Information Sciences, Fujian Agriculture and Forestry University, Fuzhou 350002, China

2 School of Mobile Network, Nanjing Technology University Pujiang Institute，Nanjing 21134，China

3 School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

4 National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China

5 School of Electrical and Information Engineering, the University of Sydney, NSW, Australia

*The corresponding author, E-mail: riqing.chen@fafu.edu.cn

I. INTRODUCTION

Recently, full-duplex relaying systems have been intensively investigated due to a wide coverage area and high spectral efficiency[1]. The full duplex operation by supporting concurrent transmission and reception in a single time/frequency channel is expected to be implemented in future generation networks[2,3]. The promise of nearly doubled channel capacity and spectral efficiency compared to conventional half-duplex communications is the most attractive feature in full-duplex communications [4,5]. However, in full-duplex systems, self-interference at the relay, due to the signal leakage from its transmitter to the receiver, will lead to a serious degradation of the system performance. Therefore, one of the key challenges in full-duplex relaying systems is how to manage and control the effect of self-interference successfully and effectively.

There are several strategies proposed for mitigating self-interference in full-duplex relaying systems [6-14]. In particular, in multiple-input multiple-output (MIMO) based on full-duplex relaying systems, beamforming schemes can be optimized for spatially suppressing the self-interference by utilizing the degree of freedom provided by multiple antennas [10-14]. In [10], the authors consider an amplify-and-forward (AF) based MIMO relaying system with full-duplex transmissions.To deal with the self-interference at the relay,the authors maximize the signal-to-interference ratio at both the input and output of the relays. However, this work neglects the effect of noise. In [11], the authors adopt a twoway full-duplex MIMO relaying system with AF protocol. Instead of purely suppressing the self-interference, the authors improve the system achievable rate by jointly optimizing the beamforming matrix at the relay and the power allocation at the two sources.

For full-duplex MIMO relay systems with the decoded-and-forward (DF) protocol, several typical beamforming schemes, such as minimum mean square error (MMSE) and nullspace projection (NSP) are investigated [12-14]. The basic idea of the null-space projection is that it forces the self-interference to be zero by designing the receive and transmit beamforming matrices. However, these schemes are not designed to achieve the optimality of the system in terms of achievable rate.

In this paper, we focus on the optimization of beamforming coefficients in a full-duplex MIMO relaying system consisting of one source, one DF-based relay and one destination. We propose an iterative beamforming structure (IBS) at the relay for enhancing the system achievable rate by alternately maximizing the average signal-to-interference-plus noise ratio (SINR) at receiver and average signal to-leakage-plus-noise ratio (SLNR) at transmitter. Although the proposed structure achieves an improved performance, there still exists residual self-interference and noise. It is a challenge to design an optimal low-complexity detector in the presence of residual self-interference which is not white. Therefore, we then develop a low-complexity maximum likelihood (ML) detector at the relay with an improved decoding performance by using whitening- filter, singular-value decomposition(SVD), and eigenvalue decomposition (EVD).

Our contributions in this paper are as follows. We first maximize the SINR, namely,Max-SINR, at the input of the relay by optimizing its receive antenna beamforming coefficients. At the same time, we maximize the SLNR, namely, Max-SLNR, at the output of the relay by optimizing its transmit beamforming coefficients. Then an iterative beamforming structure is designed to optimize the receive and transmit beamforming in an iterative manner. For the detector, wefirst design an interference-and-noise whitening filter(WF) for the colored interference-plus-noise.Then a beamforming scheme based on SVD is employed to transform the spatially coupled source-to-relay channels to independent parallel ones. Simulations show that the proposed IBS achieves much better rate and error performance within a few iterations compared with its counterparts. Also, the bit rate error performance of our low-complexity ML detector is better than the conventional ML detector with a much reduced complexity.

This paper is organized as follows. The system model is described in Section II. Section III presents the design of the IBS. Section IV describes the low complexity ML detector.The simulation results are shown and discussed in section V, and Section VI concludes this entire paper.

Notations: Throughout the paper, matrices and vectors are denoted by letters of bold upper case and bold lower case, respectively.

II. SYSTEM MODEL

As shown in Fig. 1, we consider a two-hop link between a multi-antenna source node and a multi-antenna destination node with a full-duplex DF relay connecting them. The source and destination are equipped withandantennas, respectively. The relay hasreceive andtransmit antennas. The source transmits data towards the relay, while upon receiving the signal from the source,the relay regenerates the source’s information, and transmits it towards the destination using the same frequency band. Here, it is assumed that the direct source-to-destination link is blocked, for example, due to shadow fading and path loss. Letandrepresent the source-to-relay and relay-to-destination channel matrices, respectively. The self-interference channel matrix is denoted byAll the channels are assumed to experience Rayleigh fading and the perfect CSI’s are available at the relay. The signal vectortransmitted from the source is assumed to be taken from an M-QAM constellation with the power constraintwhereis the transmit power at the source.

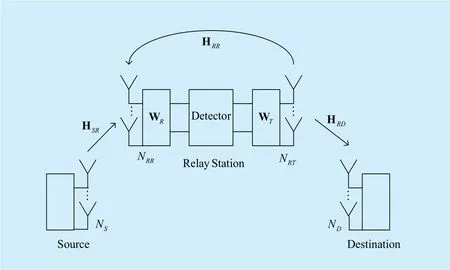
Fig.1 System model consisting of one source, one relay, and one destination

In order to further suppress interference and improve the error performance, we introduce the transmit beamformingat the relay, and thenis given by

Since we consider the DF protocol, the endto-end achievable rate can be formulated as[15]

We have

In the following section, we will enhance the achievable system rate R in Eq. (5) by optimizing the design of the beamforming matricesandat the relay.

III. ITERATIVE BEAMFORMING STRUCTURE AT THE RELAY

In this section, we propose a novel beamforming structure at the relay for improving the system achievable rate R. Since R is determined byand, we will alternatively focus on maximizing both the SINR at the relay’s input and the SLNR at the relay’s output.

First, based on Eqs. (1～3), the average SINR at the relay receiver can be written as

From (1), the average leakage of the transmit signalto the relay receiver is of the formTherefore, the SLNR at the relay transmitter can be written as [16,17]

3.1 Maximization of: Fix Optimize

For more details of the optimization process please see Appendix A. By optimizing the receive beamforming matrixwe jointly suppress the self-interference and noise to enhance the useful signal.

3.2 Maximization of: Fix Optimize

A detailed optimization process follows a similar deriving process in Appendix A.

By optimizing the transmit beamforming matrixwe reduce the leakage part of the transmit signal at the relay and improve the useful relay-to-destination part of the transmitted signal.

3.3 Iterative beamforming structure

Based on the optimization processes in the previous two subsections, we thereby propose an iterative beamforming structure (IBS) at the relay as indicated in Fig. 2 by optimizingandin an alternating iterative manner. The IBS is described as follows. Wefirst utilize the initial value ofto obtain the optimalby solving the maximization ofThen this optimizedis utilized to obtainby solving the maximization ofBy doing this process iteratively, wefinally arrive at our solutions ofand

Additionally, in order to have a good initial value ofwe define

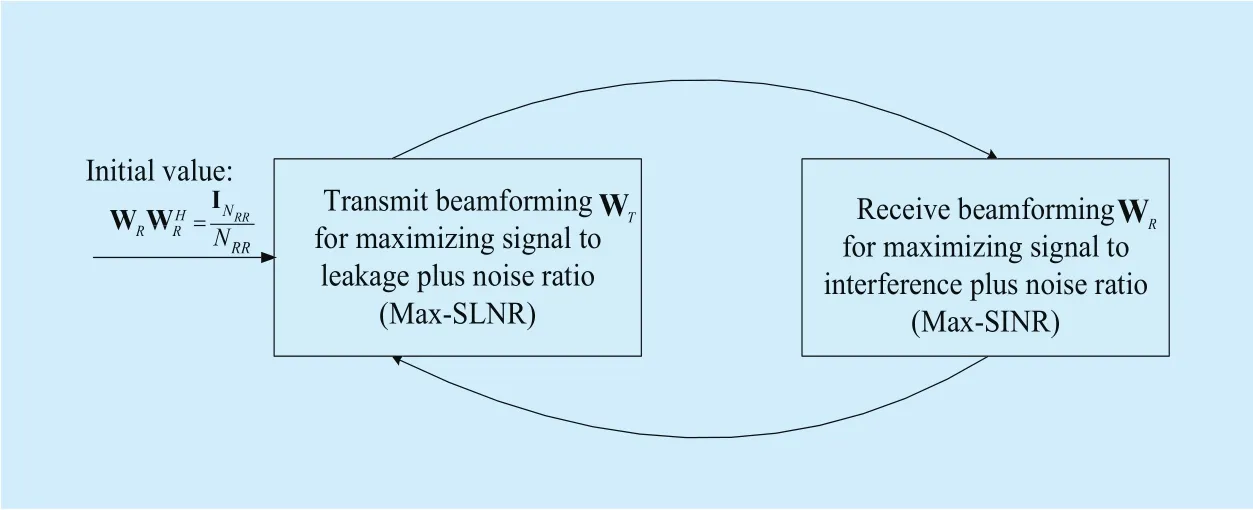
Fig.2 Proposed iterative beamforming structure at the relay

Then we substitute (13) into (12) to obtain the initial value ofwhich consists of the eigenvectors corresponding to the largesteigenvalues of the matrix

To make clear, the IBS operations are summarized as an algorithm below.

VI. INTERFERENCE-AND-NOISEWHITENING BEAMFORMING FOR ML DETECTION

In this section, we will propose an interference-and-noise-whitening beamforming method for reducing the complexity of the conventional ML detection at the relay. We rewrite Eq. (1) as

4.1 Conventional ML detector

For the conventional ML detection in a white Gaussian channel, the detecting problem of source transmitted signal at the relaycan be casted as

which has an exponential complexity in the number of the source transmit antennas,i.e.,float point operations (FLOPs),whereis the number of points in the signal

?

4.2 Proposed whitening- filter-based ML detector

with

Based on the new model in (20), we get the optimal ML detector, namely, whitening filter ML (WFML), as follows

Theorem 1: The conventional detector in Eq. (17) is equivalent to our WFML detector in Eq. (22), under the conditionwhere is a positive value. Additionally, this condition approximately holds for the largescale MIMO cases.

Proof: Please see Appendix B.

Although the proposed WFML detector in(22) has the optimal detection performance, it still has an exponential complexity ofFLOPs. In what follows, we will present an equivalent low-complexity form of our WFML detector from the beamforming viewpoint.

4.3 Proposed low-complexity WFML detector

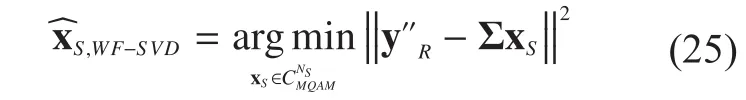
V. SIMULATIONS

In this section, we evaluate the performance of the proposed schemes and compare them with the conventional ones. The system parameters in our simulation are set as follows:andAll the channels are modeled by Rayleigh block-fading.

To observe the convergence of the proposed IBS in Section III, Fig. 3 demonstrates the curves of achievable ratesversus the number of iterations. We consider three different SNR values, i.e.,dB, 5dB, and 10dB.For all the three SNR values, the proposed IBS converges rapidly, i.e., in about four iterations.With the increment of SNR，the required number of iterations will also become larger.

Fig.3 The system achievable rate R versus the iteration numbers for the proposed IBS with different SNR values

Fig.4 Comparisons of the system achievable rate under different beamforming schemes

Fig.5 BER performance under different combination schemes for 16QAM

Fig.4 compares the achievable rateof the proposed IBS with the ones of two other beamforming schemes and the case of no mitigation. Thefirst benchmark is the null-space projection (NSP) scheme in [12], where the self-interference at the relay is forced to zero via the null-space projection. The second one is the MMSE scheme in [13], where the receive beamformingat the relay is designed based on the MMSE criterion. Additionally,we consider the scheme without the mitigation of interference, i.e., where bothandare identity matrices. It can be observed that the proposed IBS performs much better than the other three schemes in all SNR regions. And the curve of no mitigation tends to be smoothly convergent with a lowest system achievable rate. It has about a 2.5dB gain compared with the second best scheme, i.e., MMSE for the given achievable rate above 15bits/bit/Hz.The main reason for its superiority is that the proposed IBS fully takes both the self-interference and noise into account. Suppose the proposed IBS requiresiterations, then the complexity of the proposed IBS istimes those of NSP and MMSE considering the three schemes use matrix decomposition to compute the beamforming coefficientsFLOPs per matrix decomposition).

We further evaluate the bit error rate (BER)performance of our low-complexity WFML detector proposed in Section IV, namely,LCWFML. We compare our LCWFL with the conventional ML detector for Gaussian channels, namely, CML. We will investigate the BER performance for these two detectors combined with the four aforementioned beamforming schemes at the relay. As such,we have the following combination schemes:LCWFML+IBS, CML+IBS, LCWFML+NSP, CML+NSP, LCWFML+MMSE,CML+MMSE, LCWFML+No Mitigation, and CML+No Mitigation.

Fig.5 and Fig. 6 show the BER performance versus SNR for different combination schemes for 16QAM and 64QAM, respectively. From the two figures, it is obvious that the BER performance of the proposed LCWFML+IBS as well as CML+IBS is much better than the other schemes. For a given detector, the proposed IBS is better than MMSE, NSP, and No Mitigation. In particular, the IBS has adB gain at thefor 16QAM and 4dB gain at thefor 16QAM, compared with the second best scheme MMSE. Additionally,for a given beamforming scheme, e.g., IBS,MMSE, and NSP, wefind that the BER curves of the proposed LCWFML detector are slight-ly better than those of the CML. On the other hand, in the case of No Mitigation, the BER performance of our LCWFML detector is better than that of the CML with an obvious gain.The reason behind this is as follows. When using IBS, MMSE, or NSP at the relay, the residual self-interference is very small compared to the useful signal and can be omitted. For No Mitigation, the self-interference at the relay is much stronger and colored, and thus the whitening filter enables that the LCWFML detector in (22) outperforms the CML detector.

VI. CONCLUSION

In this paper, we proposed a high-rate beamforming design and a low-complexity ML detector at the relay in a DF-based full-duplex MIMO relay network. The proposed IBS achieves a high-performance rate by alternately optimizing the transmit and receive beamforming. Additionally, a low-complexity ML detector combining the WF and SVD was designed. From our simulations, we found that the proposed IBS converges within only four iterations, and performs much better than the existing beamforming schemes such as NSP and MMSE in terms of both achievable rate and BER performance. The IBS shows about 5dB gain over the MMSE atfor 16QAM. Additionally, for a given beamforming scheme, the BER performance of the proposed detector is better than that of the conventional with a lower-complexity.

Appendix A: Derivation of the optimal solution of Max-SINR

For the convenience of proof below, we first consider the caseGiven a fixedmaximizingin(9) can be formulated as

where w is a row vector, and

Fig.6 BER performance under different combination schemes for 64QAM

Although we can view the optimization problem in (27) as a generalized Rayleigh-Ritz ratio and directly give the optimal solution similar to the Max-SLNR in [16]. A strict proof need to be presented to guarantee that the optimal solution holds. Thus, in what follows, we will propose a detailed rigorous mathematical derivation for the optimal solution to the maximization problem in (27).

Considering that scaling w by any scalar does not change the value of the objective function of the problem (27), the problem (27)may be simplified to the following unconstrained maximization problem

To solve the above problem, let usfirst defineThen, the optimization problem (29) can be formulated as

which can be explained as the problem offinding the largest one from all’s satisfying the following constraint

which implies that the partial derivative of the functionwith respect tosatisfies

This means that the problem offinding the optimaland w can be found by solving the following equation

Appendix B: Proof of Theorem 1

For the convenience of the proof below, let us first defineThen we have

which means that the optimization problem in(22) achieves the same optimal value as the optimization problem in (17). This is only a sufficient condition for the equivalence between (17) and (22).

ACKNOWLEDGEMENTS

This work was supported in part by the National Natural Science Foundation of China(Nos. 61271230, 61472190, and 61501238),the Open Research Fund of National Key Laboratory of Electromagnetic Environment, China Research Institute of Radiowave Propagation (No. 201500013), the open research fund of National Mobile Communications Research Laboratory, Southeast University, China (No.2013D02), the Research Fund for the Doctoral Program of Higher Education of China (No.20113219120019), the Foundation of Cloud Computing and Big Data for Agriculture and Forestry (117-612014063), the China Postdoctoral Science Foundation (2016M591852),and Postdoctoral research funding program of Jiangsu Province (1601257C).

[1] Bliss D, Parker P, Margetts A, “Simultaneous transmission and reception for improved wireless network performance”,in Proceedings of IEEE Computer Society Workshop on Statistical Signal Processing.,pp 478-482, August, 2007.

[2] Rankov B, Wittneben A, “Spectral efficient protocols for half-duplex fading relay channels”,IEEE Journal on Selected Areas in Communications, vol. 25, no. 2, pp 379-389, February, 2007.[3] Zhang Z, Chai X, Long K, et al, “Full duplex techniques for 5G networks: self-interference cancellation, protocol design, and relay selection”,IEEE Communications Magazine, vol. 53,no. 5, pp 128-137, May, 2015.

[4] Zou Y L, Zheng B Y, Zhu J, “Outage analysis of opportunistic cooperation over rayleigh fading channels”,IEEE Transactions on Wireless Communications, vol. 8, no. 6, pp 3077-3085, June,2009.

[5] Zou Y L, Zheng B Y, Zhu J, “Performance evaluation of half-duplex relay-based opportunistic cooperation diversity”,Sciece China Information Sciences, vol. 53, no. 2, pp 325-334, February,2010.

[6] Riihonen T, Haneda K, Werner S, Wichman R,“SINR analysis of full-duplex OFDM repeaters”,in Proceedings of IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, vol. 51, no. 3, pp 3169-3173, September, 2009.

[7] Haneda K, Kahra E, Wyne S, et al, “Measurement of loopback interference channels for outdoor-to-indoor full-duplex radio relays”,in Proceedings of fourth European Conference on Antennas and Propagation，pp 1-5, April, 2010.[8] Hamazumi H, Imamura K, Iai N, et al, “A study of a loop interference canceller for the relay stations in an SFN for digital terrestrial broadcasting”,in Proceedings of IEEE Global Telecommunications Conference, vol. 1, no. 4, pp 141-150, December, 2000.

[9] Nasr K M, Cosmas J P, Bard M, et al, “Performance of an echo canceller and channel estimator for on-channel repeaters in DVB-T/H networks”,IEEE Transactions on Broadcasting,vol. 53, no. 3, pp 609-618, September, 2007.

[10] Lioliou P, Viberg M, Coldrey M, et al, “Self-interference suppression in full-duplex MIMO relays”,in Proceedings of IEEE Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers (ASILOMAR),pp 658-662. November, 2010.

[11] Zheng G, “Joint beamforming optimization and power control for full-duplex mimo twoway relay channel”,IEEE Transactions on SignalProcessing, vol. 63, no. 3, pp 555-566, February,2015.

[12] Riihonen T, Werner S, Wichman R, “Mitigation of loopback self-interference in full-duplex MIMO relays”,IEEE Transactions on Signal Processing, vol. 59, no. 12, pp 5983-5993, December, 2011.

[13] Riihonen T, Werner S, Wichman R, “Spatial loop interference suppression in full-duplex MIMO relays”,in proceedings of IEEE Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, pp 1508-1512,November, 2009.

[14] Sung Y, Ahn J, Van Nguyen B, et al, “Loop-interference suppression strategies using antenna selection in full-duplex MIMO relays”,in proceedings of IEEE International Symposium on Intelligent Signal Processing and Communications Systems (ISPACS), pp 1-4, December, 2011.

[15] Wang B, Zhang J, Host-Madsen A, “On the capacity of MIMO relay channels”,IEEE Transactions on Information Theory, vol. 51, no. 1, pp 29-43, January, 2005.

[16] Sadek M, Tarighat A, Sayed A H, “A leakage-based precoding scheme for downlink multi-user MIMO channels”,IEEE Transactions on Wireless Communications, vol. 6, no. 5, pp 1711-1721, May, 2007.

[17] Shu F, Tong J J, You X H, et al, “Adaptive robust Max-SLNR precoder for MU-MIMO-OFDM systems with imperfect CSI”,Science China Information Sciences, vol. 59, no. 6, pp 1-14, June,2016.