线性方程组的案例教学

陈永鹏

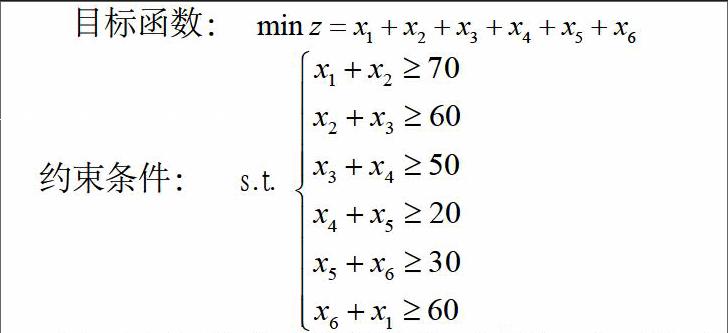
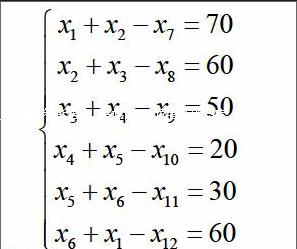
【摘 要】在目前的线性代数教学中，过于强调数学的严谨性和系统性，缺少线性代数与实际相结合的教学.在国家大力倡导应用型人才培养的大背景下，这种状况需要改变。本文考察了在线性方程组的教学中，案例教学的应用。对线性代数的实际应用进行尝试性教学。

【关键词】线性方程组；案例教学

线性代数课程在大学数学中占有重要地位，这使得广大数学教育工作者对其教学内容，教书手法进行了大量的研究.就目前的大部分教学内容来看，过于强调数学的严谨性和系统性，缺少线性代数与实际相结合的教学.使学生对这门课程只是学会了一些理论，而不知道线性代数的实际应用。在国家大力倡导应用型人才培养的大背景下，这种情况是需要改变的。也就是在线性代数教学中，要适合地融入案例教学，以提高学生的实际运用水平和学习兴趣。本文作者就线性方程组的案例教学进行了这方面的尝试。

在32学时的线性代数教学中，线性方程组是核心内容，利用初等行变化求解线性方程组也是学生必须掌握的手法。但是讲完这章以后，作者发现学生只是会了求解线性方程组，往往对其实际应用很模糊，就慢慢地在教学中融入案例教学。让学生感到学有所用的同时，强化了学生的应用意识，培养学生应用能力， 进而增强了学生对知识的掌握和理解。

本文将给出几个典型的线性方程组应用实例。

1. 人力资源分配问题

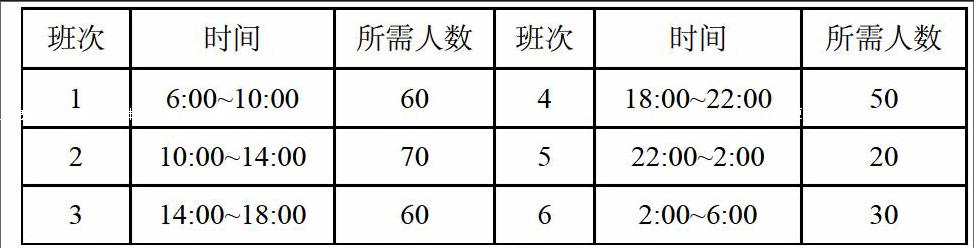
例1. 某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数表所示。

设司机和乘务人员分别在各时间段开始时上班，并连续工作8小时，问该公交线路应怎样安排司机和乘务人员，既能满足工作需要，又使配备司机和乘务人员的人数最少？

解：设表示第i班次时开始上班的司机和乘务人员数，

这样我们建立如下的数学模型。

这本来是运筹学中的线性规划模型，在线性代数中，我们只考察约束条件，这和线性方程组非常相似，但是不一样。为了转化成方程组，首先引进6个变量让六个约束左边分别减去这六个变量，则得到如下线性方程组：。

2. 套裁下料问题

例2. 某钢管零售商从钢管厂进货，将钢管按照顾客的需求切割后售出. 从钢管厂进货时得到原料钢管都是19m长. 现有一客户需要50根4m长，20根6m长和15根8m长的钢管，应如何下料最节省？

解：首先考察所有的下料方案，见[1]。通过下料方案可以引进7个变量。用表示按照第i种模式（i=1，2，…，7）切割的原料钢管的根数。这样我们建立如下的数学模型。

3. 生产计划问题

生产计划问题

例3.某公司面临一个是外包协作还是自行生产的问题。该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间。甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量。数据如表。问：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？

通过以上分析，可建立如下的数学模型：

目标函数： max=

约束条件：

为了转化成方程组，首先引进3个变量让三个约束左边分别减去这三个变量，则得

到如下线性方程组：

通过以上两个案例，就把线性方程组与实际问题联系起来了。使学生了解了线性方程组是如何应用于实际的，进而对这门课程的理论有了新的认识，提高了学习兴趣，从而增强了学生的应用意识。另外为了求解这些方程組，可以在教学中融入数学软件 Matlab、Mathematic，从而使学生更加觉着线性代数不仅有用，而且好学。

参考文献：

[1] 谢金星，薛毅. 优化建模与lindo/lingo软件[M]. 北京：清华大学出版社，2005.

[2] 黄玉梅. 应用型人才培养的《线性代数》课程教学改革探索[J]. 西南师范大学学报（自然科学版）， 2013， 38（11），157-161.

基金项目：

基于高校转型发展的大学数学课程模块化教学改革研究与实践（项目编号：2015JGA425）.