膨胀性土壤降雨入渗产流模型

甘永德，贾仰文，刘 欢，牛存稳，仇亚琴

（中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038）

1 研究背景

降雨入渗是指降雨通过地表向下运动，补给土壤水、地下水的过程，是水文过程的重要环节。当前，在非膨胀性土壤入渗水分运动过程研究方面，国内外学者已经开展了大量室内外试验，并建立了相关数学模型，如 Green&Ampt［1］、Richards［2］、Philip［3］、Jia［4］、甘永德［5］、杨大文［6］和朱磊［7］等。然而，这些针对刚性土壤的研究成果并不适用于膨胀性土壤水分运动过程的研究。我国是世界上膨胀性土壤分布广泛的国家之一。膨胀性土壤吸水膨胀，失水收缩，这种湿胀干缩特性不仅影响到土壤水分运动过程，也会给工程建设带来一系列问题，其已成为工程地质学、水文学和土力学等学科关注的重点。

土壤膨胀变形主要与初始含水量和上覆荷载有关，膨胀力和膨胀变形随土壤增湿程度增加而增加［8］。在吸水膨胀过程中，土壤膨胀变形多表现为垂直向上［9］。Garnier等［10］基于欧拉描述（ED）和拉格朗日描述（LD）模拟分析了变形土壤的水力传导率。McGarry等［11］研究了土壤含水量与土壤变形量间的关系，并提出了用于描述土壤湿胀干缩变化特征的三直线模型。土壤应力-应变关系一般采用对数函数描述［12］。Smiles［13］以达西-白金汉和连续方程为基础，推求了膨胀性土壤中的物质能量平衡方程。苏宁虎［14］采用分数阶偏微分方程（fFPE）建立了膨胀性土壤入渗方程。土壤吸水膨胀变形主要受膨胀力和自重应力的作用，其中膨胀力随土壤含水量变化，自重应力随土壤深度变化。土壤受力变形特征随土壤深度发生改变，引起土壤饱和含水量、饱和导水系数、饱和比容积等参数的变化，进而改变着土壤剖面水分入渗过程。然而，当前针对膨胀性土壤变形对降雨入渗产流过程的影响研究仍处于探索阶段，相关模型研究尚不成熟。

本文以Green-Ampt模型为基础，提出了考虑土壤膨胀变形的降雨入渗产流模型，并通过开展室内不同厚度土壤的降雨入渗产流试验，对该模型作了验证。相关研究有助于完善土壤水分运动理论，对膨胀性土壤水分管理与调控具有一定的指导价值。

2 膨胀性土壤降雨入渗产流模型

取地面为参照面，以向下为正（图1）。膨胀性土壤吸水膨胀变形，此时土壤的变形同时受到土壤膨胀力和自重应力的作用。土壤吸水膨胀变形后，土壤湿润区剖面饱和导水系数和饱和含水量会随土壤深度发生变化。为了便于分析，做如下假设：（1）变形前的土壤为均质土壤；（2）土壤变形为弹性变形，即变形无滞后性；（3）土壤变形只引起土壤孔隙度发生变化；（4）入渗过程中土壤剖面存在明确的湿润锋面，湿润锋面将湿润区和未湿润区截然分开，湿润区土壤达到饱和，未湿润区土壤含水量为初始含水量。为了便于描述土壤导水系数随土壤深度的变化特性，引入膨胀性土壤导水系数Ks(e)描述湿润区土壤导水系数；引入膨胀性土壤饱和含水量θT描述湿润锋以上土壤饱和含水量。由此，本文基于Green-Ampt模型提出了考虑土壤膨胀性的降雨入渗产流模型GJGAM（Gan and Jia pro⁃pose a modified Green-Ampt model），与传统不考虑土壤膨胀性的Green-Ampt模型TGAM（Traditional Green-Ampt model）相比，该模型量化了土壤膨胀变形引起的土壤导水系数和饱和含水量的变化。

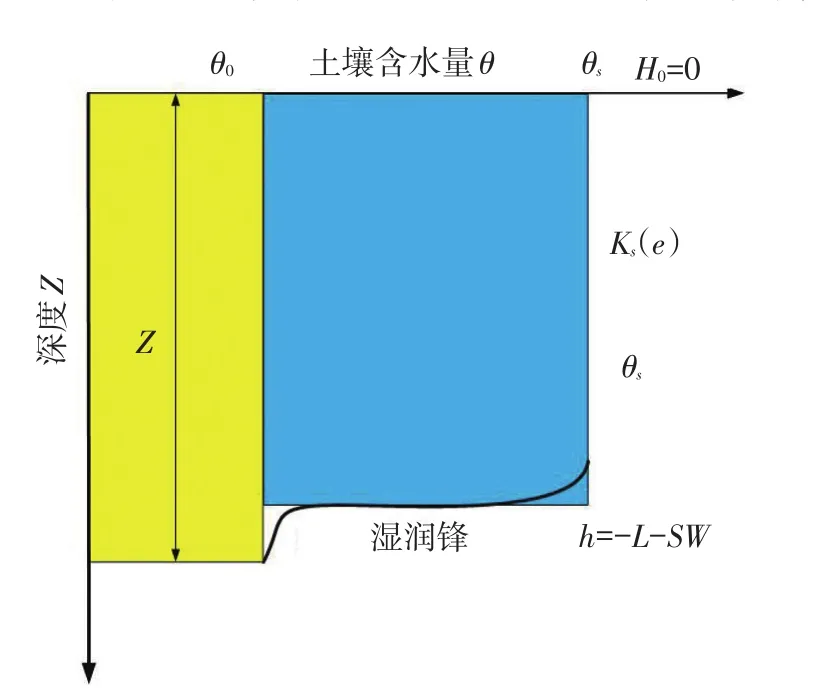
图1 土壤入渗过程示意图

土壤吸水膨胀变形是土壤膨胀力和自重应力共同作用的结果，假设土壤膨胀变形是由土壤孔隙度的变化引起的，则当土壤饱和时，土壤膨胀力引起的孔隙度变化量可以表示为：

式中：ρd为土粒密度，g/cm3；e0为土壤初始孔隙度，cm3/cm3；∆ew为由土壤吸水膨胀导致的孔隙度变化量，cm3/cm3；ρsw为由土壤吸水膨胀导致的容重变化量，可以采用土壤膨胀特征曲线计算（三直线模型结构段计算［11］）：

式中：c和α3均为三直线模型参数；U为土壤质量含水量，g/g；

同理，土壤自重应力引起的孔隙度变化量可以表示为：

式中：∆ep为由土壤自重应力导致的孔隙度变化量，cm3/cm3；ρsp为由土壤自重应力导致的容重变化量，可以采用土壤应力-应变关系曲线计算［12］：

式中：γ为土壤湿比重，N/cm3；Z为土壤深度；A和B均为参数。

在土壤膨胀力和自重应力的合力下，土壤孔隙度变化量可以表示为：

当土壤饱和时，土壤孔隙被水分充满，即土壤饱和含水量等于孔隙度，则土壤剖面饱和含水量总量θT可以表示为：

式中：θT为土壤深度Z以上区域的饱和含水量，cm3/cm3；Z为土壤深度，cm。

受土壤膨胀变形影响，土壤饱和导水系数随深度而变化。针对土壤饱和导水系数，采用改进的Lambe模型［15］计算：

式中：Ks(e)为孔隙度为ez时土壤饱和导水系数，cm/min；ez为土壤深度为Z时土壤孔隙度；K0为孔隙度为e0时土壤饱和导水系数，cm/min；m为与土壤孔隙度性质有关的参数。

由于降雨过程中，雨强是非恒定的。因此，将降雨过程划分为x个时段，每个时段内降雨强度恒定，x（x∈ 0,1,...,n），n为时段数。同一降雨时段（tx-1～tx）内，降雨入渗特性由本时段的降雨强度I、时段初的积水深度h0和潜在入渗强度fpt决定。由于积水深度h0与雨强单位不同，模型计算时，将h0除以相应时段，转换为雨强P’。根据时段内降雨强度、时段初积水深和潜在入渗强度，时段内入渗过程可以分为以下情景（图2）：

图2 积水过程和非积水过程转换情景示意图

图2（a）h0=0，其中Ks(e)为膨胀性土壤湿润区导水系数；I为雨强；h0为时段初积水深度；fpt为积水入渗率。这种情况下，随着降雨的持续进行，地表开始积水，土壤入渗过程可以分为非积水入渗过程和积水入渗过程；图2（b）h0＞0，P’+I＜Ks(e)≤fpt。这种情况下，随着入渗过程的进行，土壤积水全部渗入土壤，土壤开始进行非积水入渗过程。土壤入渗过程分为积水入渗过程和非积水入渗过程；图2（c）h0＞0，P’+I≥fpt≥Ks(e)。这种情况下，土壤持续进行积水入渗过程；图2（d）h0=0，I＜Ks(e)≤fpt.。这种情况下，土壤持续进行非积水入渗过程。

根据达西定理有：

积水前：

积水后：

忽略地表积水：

式中：fnpt为积水前入渗强度，cm/min；I为雨强，cm/min；fp为积水后土壤入渗率，cm/min；SW为湿润锋土壤水吸力，cm；H0为积水深度，cm；Z为湿润锋距离，cm。

由水量平衡原理，可以得出某一时刻t的累计入渗量F可以表示为：

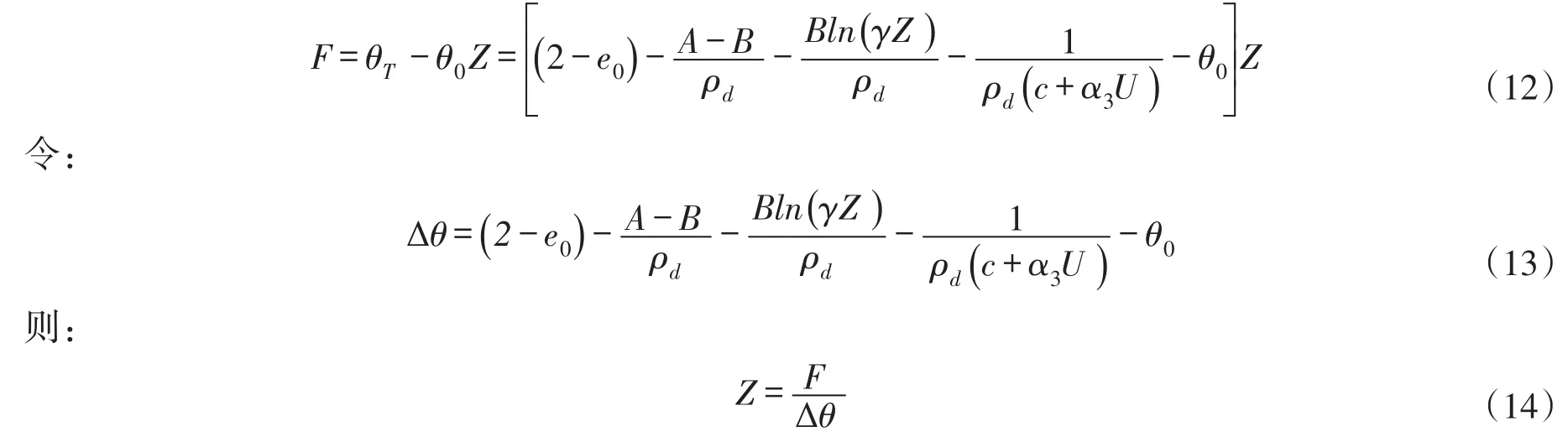
式中：θT为湿润锋以上土壤饱和含水量，cm3/cm3；F为土壤累计入渗量，cm。

积分得：

积水时刻确定：

式中：fnpt为非积水时段入渗强度，cm/min；Fp积水发生时刻土壤累计入渗量，cm；F为土壤累计入渗量，cm；tp为土壤表层积水发生时间，min；Ip为土壤表层积水发生时的时段降雨强度，cm/min；I为x时段降雨强度，cm/min；fpt为积水时段土壤入渗率，cm/min；t为时间，min；q0为土壤初始含水量，cm3/cm3；qT为湿润锋以上土壤饱和含水量，cm3/cm3；SW为湿润锋平均吸力，cm；A为参数；K（se）为土壤饱和导水系数，cm/min。

3 模型验证

3.1 材料与方法

（1）试验材料：黄土具有膨胀性［16］，以娄土为典型膨胀土壤，土壤经风干，过5 mm筛备用，采用吸管法测定土壤颗粒组成（表1）。试验用水取自中科院水利部水土保持研究所所制纯净水。

（2）试验设计：膨胀性土壤吸水膨胀变形主要受膨胀力和自重应力的影响，导致土壤入渗过程随着土壤的深度而变化。为了定量分析土壤膨胀变形对土壤降雨入渗产流过程影响，试验设置4个土壤厚度，分别为10、20、30和40 cm，每个处理两个重复，分别标记为：娄土10 cm、娄土20 cm、娄土30 cm和娄土40 cm。

（3）研究方法：试验时，将经5 mm筛的土壤分层（10 cm）均匀装入土槽中，土槽中间位置深度0、10、25、40 cm处安装Trime水分传感器，用以测定土壤水分动态过程。土槽上设置两个出水口，分别为壤中流和地表径流出水口。土壤装填时，首先在土槽底部铺设具有反滤作用的石子，厚度10 cm；再在石子的上面铺设纱布，然后将过5 mm筛后的土壤按定容重（1.4 g/cm3）装入土槽。

试验进行前，向土槽内注入足够水量（要求土壤含水量达到田间持水量以上，并产生大量壤中流）后静置，待其膨胀量达到相应土壤含水量下的最大膨胀量后进行降雨试验。

试验过程中，用降雨系统进行人工降雨，每次降雨历时控制在350 min左右。试验中Trime水分测定系统记录水分动态。同时，对地表径流量、壤中流流量进行收集、量测。径流观测时间间隔，根据产流速度而定，由于壤中流退水较慢，因此加长相应的观测时间，假如试验过程中不产生壤中流，则放弃测定。试验设置雨强为30 mm/h，坡度为5°。

试验主要观测资料：径流（地表径流量、壤中径流量）、土壤剖面水分动态、产流历时、降雨强度等。

为了便于分析入渗过程，采用日本HITACHI公司生产的GR21G离心机测定土壤水分特征曲线，并用Van Genuchten模型［17］进行拟合，拟合结果见表2；采用比重瓶法测定土密度。

土壤膨胀特征曲线采用游标卡尺法测定［16］，并用三直线模型［11］进行拟合，拟合结果见表3：

式中：ν为比容积，是土壤容重的倒数，cm3/g；U为质量含水量，g/g；α1、α2、α3为土壤膨胀特征曲线斜率；UA、UB、US分别为拐点处质量含水量，g/g；a、b、c为参数。

采用恒压法测定土壤应力-应变关系曲线［12］（由于降雨影响土柱深度小于1 m，自重应力不超过25 kPa，因此恒定压力取值范围为0～25 kPa），并用对数函数进行拟合，拟合结果见表4：

式中：ρs为土壤容重，g/cm3；p为应力，N/cm2；γ为土壤湿比重，N/cm3；Z为土壤深度；A和B为参数。

采用恒体积法测定土壤容重与对应的饱和导水系数（容重分别为1.1、1.2、1.3、1.4和1.5g/cm3），并用Lambe模型［15］进行拟合，拟合结果见表5：

式中：Kse为孔隙度为e时的土壤饱和导水系数，cm/min；e为孔隙度，cm3/cm3；K0为孔隙度为e0时的土壤饱和导水系数，cm/min；m为参数。

3.2 模型参数GJGAM的主要参数包括土壤饱和含水量、初始含水量、饱和导水系数和湿润锋土壤水吸力（见表6）。受土壤膨胀力和自重应力的影响，土壤吸水膨胀后，土壤水分特征参数随着土壤的深度而变化，直接测定不同土壤深度下水分特征参数费时费力，也很难确定。本文基于笔者提出的参数计算模型，获得了不同土壤深度下的饱和导水系数和饱和含水量，计算所需参数包括土壤膨胀特征曲线、土壤应力-应变关系曲线、土密度、土壤初始容重及其对应饱和含水量、初始容重对应的饱和导水系数、与孔隙度有关的参数m等；土壤初始含水量采用实测值，分不同土壤深度给出；湿润锋吸力采用进气值一半代替，当土壤饱和时，湿润锋吸力为0。

TGAM模型认为土壤刚性，土壤在干湿交替变化过程中土壤结构保持不变。均质土壤条件下，土壤饱和含水量、饱和导水系数均不随土壤深度发生变化。当TGAM应用于膨胀性土壤时，很难确定土壤饱和水分特征参数。为了获得土壤饱和水分特征参数，本文将初始装填容重所对应的土壤饱和导水系数和饱和含水量应用于模型；土壤初始含水量采用实测值，按不同土壤深度实测值给出；湿润锋吸力采用进气值一半代替（表7）。

表1 土壤基本物理性质

表2 van Genuchten模型拟合参数

表3 三直线模型拟合参数

表4 土壤应力-应变关系曲线

表5 Lambe模型拟合参数

4 结果与讨论

4.1 径流强度实测和模拟的径流强度随时间的变化关系如图3所示。可以看出，对于所有土壤深度处理，稳定降雨条件下，径流强度随着时间而增大，然后趋于稳定。就产流时间而言，GJGAM和TGAM计算得到的径流产流时间均先于观测值。就径流强度而言，当土壤深度处理为10 cm时，TGAM较大估计了径流强度，而当土壤深度处理大于10 cm时，TGAM较小估计了径流强度；GJGAM对径流强度的模拟值更接近于实测值，两者较吻合。

表6 GJGAM模型输入参数

表7 TGAM模型输入值

径流强度实测值与模拟值间的相对误差、均方根误差和Nash效率系数统计见表8。可以看出，对于所有土壤深度处理，GJGAM得到的径流强度模拟值与实测值间的ARE大于-17.0%；RMSE小于0.011 cm/min；Nash效率系数均大于0.51。TGAM得到的径流强度模拟值与实测值间ARE在-53.26%～-5.08%；RSME均大于0.014；Nash效率系数在-18.26～0.20之间，这说明通过考虑土壤膨胀性对降雨入渗产流过程影响，GJGAM极大提高了对径流强度的模拟精度。

出现这种情况的原因可能是，娄土具有膨胀性，土壤吸水膨胀变形过程是土壤膨胀力和自重应力共同作用结果。当土层较薄时，土壤自重应力较小，土壤在膨胀力作用下，土壤体积增大，导致孔隙度增大，土壤饱和含水量、饱和导水系数均增大；随着土壤厚度的增大，土壤自重应力增大，土壤的自重应力开始起到主导作用。土壤在自重应力作用下，土壤体积减小，孔隙度减小，导致土壤饱和含水量和饱和导水系数均减小。因此，当土层较薄时，TGAM较小估计了土壤入渗量，进而较大估计了径流强度，反之亦然。

图3 径流强度随时间变化关系

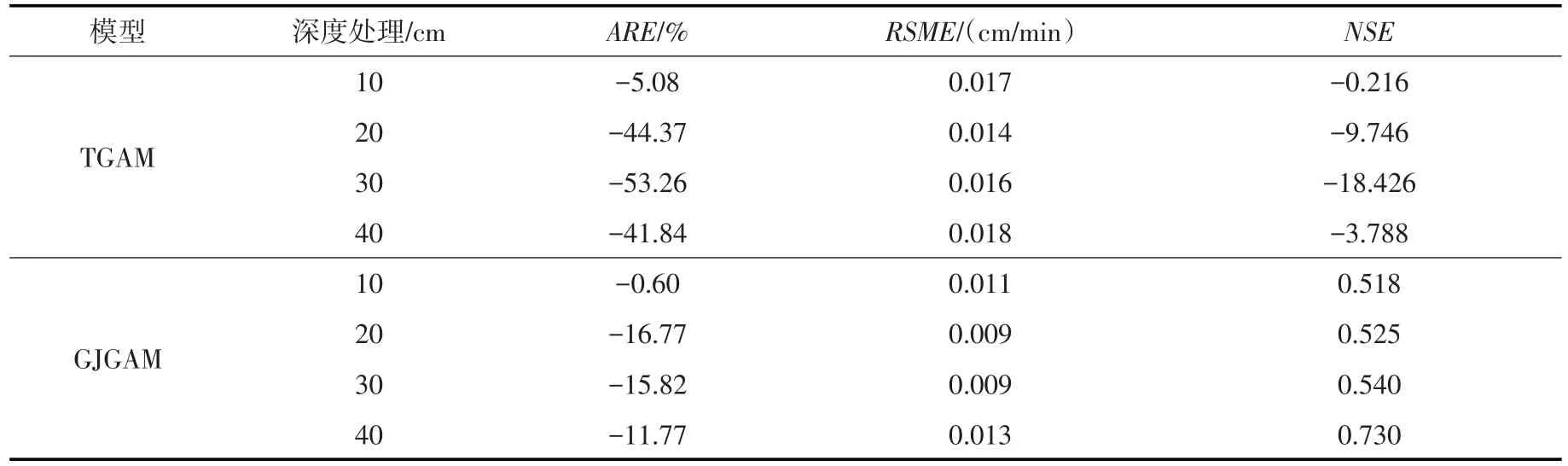
表8 径流强度实测值与计算值间相对误差（ARE）、Nash效率系数及均方根误差（RMSE）统计

4.2 土壤累计入渗量实测和模拟的土壤累计入渗量随时间的变化关系如图4所示。可以看出，对于所有土壤深度处理，土壤累计入渗量随着时间而增大。当土壤饱和后，实测和模拟得到的土壤累计入渗量均会发生突变。出现这种情况的原因在于，土壤饱和后，湿润锋处土壤水吸力消失，土壤水在重力作用下移动。

TGAM在整个入渗过程中均较大估计了土壤累计入渗量。GJGAM在入渗初期较大估计了土壤累计入渗量，而随着时间的变化，GJGAM模拟值开始与实测值接近，逐渐等于实测值。整体而言，GJ⁃GAM模拟值与实测值接近，两者较为吻合。

土壤累计入渗量实测值与模拟值间的相对误差、均方根误差和Nash效率系数统计见表9。可以看出，对于所有土壤深度处理，GJGAM得到的土壤累计入渗量模拟值与实测值间的ARE在-7.99%～18.86%；RMSE小于0.25 cm；Nash效率系数均大于0.78。TGAM得到的土壤累计入渗量模拟值与实测值间ARE在17.95%～139.72%；RSME均大于0.35；Nash效率系数在-17.55～0.96之间。这说明，通过考虑土壤膨胀性的影响，GJGAM更适合描述膨胀性土壤的降雨入渗产流过程。

图4 土壤累计入渗量随时间变化关系

表9 土壤累计入渗量实测值与计算值间相对误差（ARE）、Nash效率系数及均方根误差（RMSE）统计

TGAM没有考虑土壤膨胀变形对土壤入渗的影响，导致模型高估了土壤累计入渗量。另外，GJ⁃GAM在入渗初期高估了土壤累计入渗量，可能的原因在于土壤膨胀变形不仅与土壤含水量及自重应力有关，而且与时间有关。土壤入渗过程中，土壤吸水膨胀，但膨胀变形过程很难及时完成，需要持续一段时间才能达到对应含水量下的变形量。但GJGAM认为，土壤变形为弹性变形，与时间无关，导致了模型无法准确模拟变形滞后对土壤入渗过程影响。

5 结论

相较于刚性土壤，膨胀性土壤中含有蒙脱石、蛭石等膨胀性矿物。这些膨胀性矿物吸水膨胀引起土体的整体变形。土壤变形是土壤膨胀力和自重应力共同作用的结果，当自重应力较小时，土壤在膨胀力作用下，土壤体积增大，导致土壤孔隙度增大，土壤入渗能力增大；随着土壤深度的增大，自重应力增大，导致土壤孔隙度减小（外在表现为湿陷性［18-19］），土壤入渗能力减小。本文引入了考虑土壤膨胀性的饱和含水量和饱和导水系数，量化了土壤膨胀性对入渗过程的影响，提出了考虑土壤膨胀性的降雨入渗Green-Ampt模型（GJGAM）。

由于GJGAM形式简单，具有较强的物理机理，便于在大尺度水文模型中应用。同时，GJGAM参数较少，物理意义明确，可以根据土壤物理性质确定，因此GJGAM具有更强的应用价值。GJGAM通过了不同厚度膨胀性土壤入渗产流试验验证，这说明该模型适用于膨胀性土壤非稳定降雨条件下的入渗产流过程模拟。此外，GJGAM具有对积水入渗过程和非积水入渗过程互相转换过程进行模拟的功能，因此该模型不仅适用于非稳定降雨入渗产流过程，也适用于稳定降雨入渗产流过程及灌溉积水入渗过程。

同时，基于膨胀性土壤室内试验，验证了GJGAM和TGAM两模型模拟的精度和可靠性。结果表明，GJGAM模拟得到的土壤累计入渗量和径流强度均与实测值较吻合，而TGAM模拟得到的土壤累计入渗量和径流强度大于或小于实测值，原因在于TGAM认为土壤为刚性土壤，土壤饱和含水量和饱和导水系数均不随土壤深度发生变化。

［1］ GREEN W H，AMPT G A.Studies on soil physics：Part I.Flow of air and water through soils［J］.The Journal of Agricultural Science，1911，4（1）：1-24.

［2］ RICHARDS L A.Capillary conduction of liquids through porous mediums［J］.Journal of Applied Physics，1931，1（5）：318-333.

［3］ PHILIP J R.Theory of infiltration［J］.Advances in Hydroscience，1969（5）：215-296.

［4］ JIA Y，TAMAI N.Modeling infiltration into a multi-layered soil during an unsteady rain［J］.Journal of Hydrosci⁃ence and Hydraulic Engineering，1998，16：1-10.

［5］ 甘永德，贾仰文，王康，等.考虑空气阻力作用的分层土壤降雨入渗模型［J］.水利学报，2015，46（2）：164-173.

［6］ 杨大文，丛振涛，等.从土壤水动力学到生态水文学的发展与展望［J］.水利学报，2016，47（3）：390-397.

［7］ 朱磊，田军仓，等.基于全耦合的地表径流与土壤水分运动数值模拟［J］.水科学进展，2015，26（3）：322-330.

［8］ 丁振洲，李利晟，郑颖人.膨胀土增湿变形规律及计算公式［J］.工程勘察，2006（7）：13-16.

［9］ 龙安宝.浅论膨胀土在胀缩变形过程中的应力应变状态［J］.四川建筑科学研究，2003，29（4）：49-52.

［10］ GARNIER P，PERRIER E，JARAMILLO R A，et al.Numerical model of 3-dimensional anisotropic deformation and 1-dimensional water flow in swelling soils［J］.Soil Science，1997，162（6）：410-420.

［11］ MCGARRY D，MALAFANT K W J.The analysis of volume change in unconfined units of soil［J］.Soil Science Society of America Journal，1987，51（2）：290-297.

［12］ 陈仲颐，周景星，王洪瑾.土力学［M］.北京：清华大学出版社，1994.

［13］ SMILES D E.Water balance in swelling materials：some comments［J］.Australian Journal of Soil Research，1997，35（5）：1143-1152.

［14］ SU N.Theory of infiltration：Infiltration into swelling soils in a material coordinate［J］.Journal of Hydrology，2010，395（1）：103-108.

［15］ LAMBE T W，WHIMAN R V.Soil Mechanics［M］.6th ed.New York：Wiley，1979.

［16］ 黄传琴，邵明安.干湿交替过程中土壤胀缩特征的实验研究［J］.土壤通报，2008，39（6）：1243-1247.

［17］ van GENUCHTEN M T，LEIJ F J，et al.The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils［M］.U.S.Salinity Laboratory，U.S.Dept.of Agriculture，Agricultural Research Service，Riverside，CA ，1991.

［18］ 杨运来.黄土湿陷机理的研究［J］.中国科学：B辑，1988（7）：756-766.

［19］ 谢婉丽，王延寿，马忠豪，等.黄土湿陷机理研究现状及发展趋势［J］.现代地质，2015，29（2）：397-407.