水电站负荷优化分配的分解聚合原理及应用

陈森林，梁 斌，卢 慧

（1.水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.武汉大学 水利水电学院，湖北 武汉 430072；3.上海市政工程设计研究总院（集团）第六设计院有限公司，安徽 合肥 230071）

1 研究背景

水电站厂内经济运行是在满足电能生产安全、可靠和优质的前提下，科学合理地安排水电机组的运行，以期获得尽可能大的经济效益，因此，开展厂内经济运行是提高水电站水能利用效率的关键。

水电站厂内负荷优化分配属于复杂的多约束混合整数非线性规划问题［1］，求解此问题的传统方法主要有：传统的等微增率法、线性规划法［1-2］、拉格朗日松弛法［3］、分支定界法［4］、混合整数线性规划法［5］和动态规划法［3-9］等。近年来，随着智能算法的迅速发展，许多学者将智能算法引入此类问题的求解，如混沌优化［10］、遗传算法［11］、免疫算法［12］和粒子群算法等各类智能算法。现行的厂内负荷优化分配问题的研究，主要集中在水力结构简单、机组独立引水的各类电站系统的模型构建和求解方法上，但随着系统水力结构的复杂化和系统规模的扩大，后效性和维数灾问题就凸显出来。智能算法有其求解非线性多约束不连续问题的先进性，但同时也存在物理机制不明晰、理论上难以证明最优性、容易收敛早熟陷入局部最优解、公式复杂参数过多、求解缓慢等（物理意义、收敛性及求解性能）问题［12-18］。同时，受社会经济的快速发展和气候变化的影响，近年来许多水库在水量出现富余的情况下不断增加或扩容机组，造成水电站引水系统管网具有复杂的水量和水力联系，导致厂内负荷优化分配数学模型更加复杂。对于复杂引水系统水电站负荷优化分配问题，其建模和运用优化技术（包括现代智能算法）求解过程均会受到系统水力联系复杂、结构不明晰的制约。因此，对于具有复杂引水系统水电站，亟待探索科学合理的、通用的、算法稳定且简单高效的厂内负荷优化分配方法。

漳河水库是一座具有防洪、灌溉、城市供水、发电、水产、航运和旅游等综合利用功能的大Ⅰ型水利工程，流域面积2 212 km2。漳河水库电站群由建成于不同时期的3座水电站组成：漳河电站2台3 000 kW机组（1号和2号）、观音寺电站3台800kW机组（3号、4号和5号）及三佳梯级串联2台160 kW机组（6号和7号，其间由尾水/前池衔接），7台机组总装机8 720 kW。该水电站群机组布置和引水管网结构（如图1所示）几乎涵盖了各种水电站类型，具有较好的研究普适性负荷优化分配方法的条件，因此，本文以此电站为背景，运用分解聚合原理，开展复杂引水系统水电站厂内负荷优化分配方法及其应用研究，以达到提出普适性的方法、实现提高机组效率和高效利用水能的目的。

2 复杂引水系统分解聚合原理

2.1 系统分解为了建立完整的复杂引水系统负荷优化分配数学模型，有必要绘制描述动力关系的包含发电机组（基础）、引水管网结构（纽带）及动力指标要素（水头）关系图（如图1），具体绘制方法步骤如下（以漳河为例）。

（1）绘制机组和引水系统结构图。根据水电站引水隧道和压力管道空间布置情况，绘制机组布置和引水系统结构图。矩形框表示机组（j号机组用U0,j表示）、椭圆形框表示串联机组间的尾水/前池，线段表示引水隧道或压力钢管，以水库和水电站尾水为上下边界。

（2）标注水力联系结点。从水库开始沿着引水隧道或压力管道水流方向，起始结点用实心圆表示（称为外结点），分流结点用空心圆表示（称为内结点）。内结点具有流量平衡制约作用，也是定义各类水头及系统分解和聚合的分界点。

（3）标注分段管道和结点间水头。相连结点间分段引水隧道或压力管道长度用L代表、相应的水头损失用∆H表示（∆H可基于管道相关数据，根据水力学公式推求），任一结点与水电站尾水之间的水头用H表示。

图1 漳河水库电站群系统水力联系结构与动力指标要素

图1可以清晰且完整地描述引水系统管道过流量和机组发电流量之间的关系、各工作单元水头之间关系。对于一个具有N台机组（实例N=7）的系统，以机组U0,n(n=1～N)为基础、内外结点为依据，依据该图可将系统分解为M级（实例M=4）子系统（用Nm表示第m级子系统的个数）。

（1）一级子系统（N1=3）：由直接引水管及串并联机组组成，包括基于H1,1的U0,1与U0,2；基于H1,2的U0,3与U0,4；基于H1,3的U0,6与U0,7串联机组（发电流量相同）。

（2）二级子系统（N2=1）：由共用引水管的一级子系统组成，包括基于H2,1的U0,3、U0,4与U0,6、U0,7。

（3）三级子系统（N3=1）：由共用引水管的二级及以下子系统组成，包括基于H3,1的机组U0,5与二级子系统U0,3、U0,4、U0,6、U0,7。

（4）四级子系统（N4=1）：由直接从水库引水的低级子系统组成，即基于Hsdz的三级子系统和一级子系统U0,1与U0,2。

通过上述分解，将该水电站群系统分解为6个不同层级的子系统，各子系统既避免了应用多阶段决策方法求解优化数学模型的后效性制约，又为构建组件式（如机组检修时可剪枝）厂内负荷分配优化数学模型奠定了基础。

2.2 系统聚合复杂系统建立的优化数学模型难以求解，以上分解的目的也是为了通过逐级子系统的优化实现全系统的优化。因此，本文引入“等效机组”概念，可将不同层级的子系统有机地聚合成相应层级的“等效机组”。

将水能发电机组记为0级等效机组、与其独立引水管组成的系统记为0级等效机组段；将共用一个引水管的各0级等效机组段组成的子系统记为1级等效机组、与其共用引水管组成的系统记为1级等效机组段；依此类推，由不大于m-1级（m≥1，至少含有1个m-1级）等效机组段并联或串联所组成的动力系统称为m级等效机组、与其共用引水管组成的系统记为m级等效机组段。同时，将并（串）联成员组成的等效机组称为并（串）联等效机组。基于这种思路，即可绘制水电站动力系统聚合关系图（图2所示）。因此，如何形成等效机组段和等效机组是实现该思路的核心与关键。

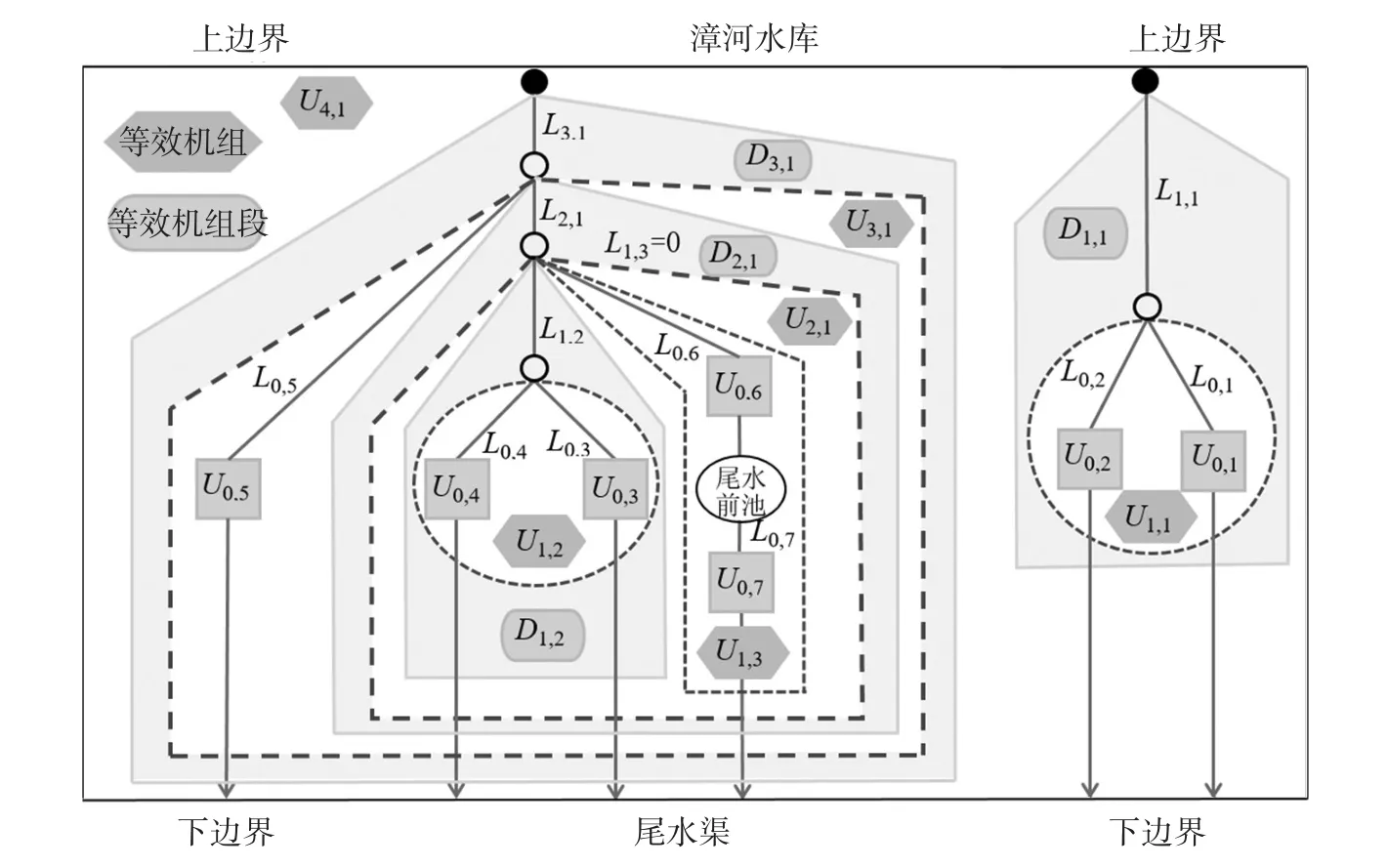
图2 漳河水库电站群系统“等效机组”聚合关系

为了便于描述，定义如下相关变量（参见图1、图2）：Um,n、Lm,n分别表示m级第n个等效机组（m=0时,n=1～N;当0＜m≤M时,n＜N，下同）及与其直接相连的引水管道；Dm,n表示Um,n对应的等效机组段；及Hm,n分别表示Dm,n的水头、Lm,n的水头损失及Um,n的水头m；∆Zk表示第k个尾水/前池水位差，m。

（1）基于物理连接关系定义等效机组段。以水头关系为基础，可以定义等效机组段，其水头等于引水管水头损失加等效机组水头。

式中：⊕表示物理连接关系，将m级第n个等效机组与直接引水管组成等效机组段。

如图2所示，D0,3=L0,3⊕U0,3表示机组段D0,3由机组U0,3及与其直接相连的引水管道L0,3组成（D0,4类同）；D1,2=L1,2⊕U1,2表示机组段D1,2由等效机组U1,2及与其直接相连的引水管道L1,2组成，其它类推。

（2）基于水量和电力联系定义等效机组。共用引水管的各机组段（子系统组成部分），可聚合成一个等效机组。

对于并联机组段，其水头相同，等效机组的发电流量和出力等于各机组段之和：

对于串联等效机组段，满足水头平衡关系，等效机组的发电流量与各机组段引用流量相同、出力等于各机组段之和：

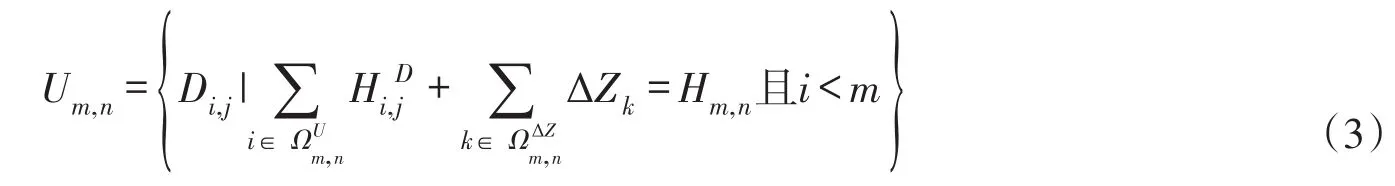
以水力联系结点为依据，将各结点分流形成的各子系统进行聚合，即可构建出复杂引水系统聚合关系图（如图2所示），从而为负荷分配优化数学模型求解奠定基础。

3 水电站负荷优化分配模型

基于系统水力联系结构与动力指标要素图（图1），可以建立“以电定水”模式的水电站群耗流量最小准则数学模型。

3.1 目标函数

式中：Hsdz为电站群毛水头，m；Nsdz为电站群总负荷，kW；θi(i= 1～6)为各机组发电流量权重；

目标函数式（4）中赋予机组发电流量不同的权重θi，既可以满足人工干预机组的投入顺序需求（优先机组权重小），又可处理机组检修问题（如日计划中机组检修的部分时段，就可以设置最大的权重）。

3.2 约束条件

（1）负荷平衡约束：

（2）机组可行出力范围约束：

式中：Ω0,i为i号机组可行出力集合，反映了机组振动、预想出力及电力线路等限制因素；Ωm,n为Um,n的可行出力集合。

（3）结点流量平衡约束：

①串联等效机组

②并联等效机组

（4）水头关系约束：

①串联等效机组

②并联等效机组

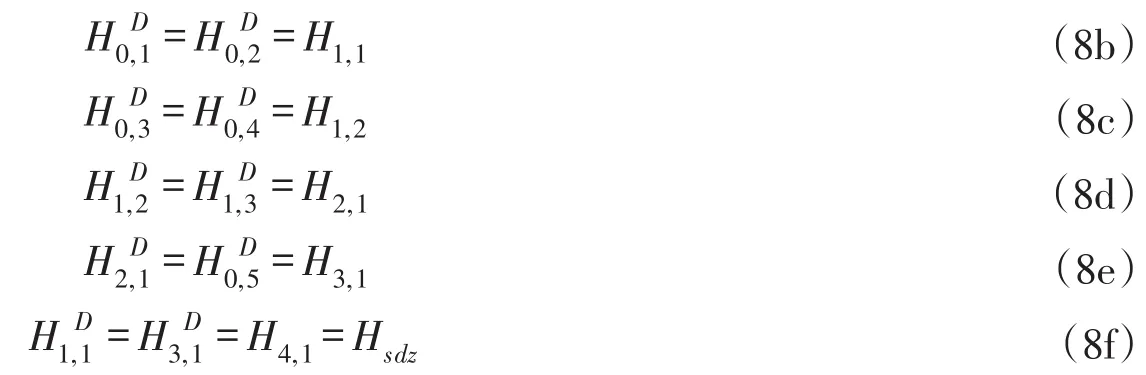
③逐级等效机组水头、水头损失与等效机组段水头间关系约束：

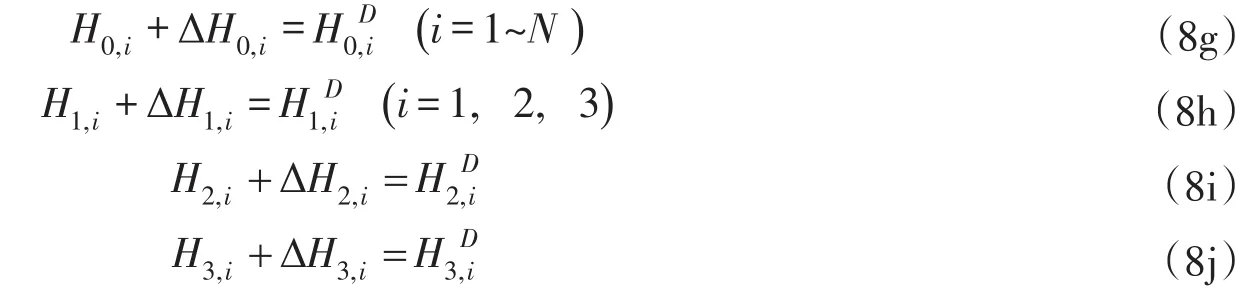
（5）水头损失与流量关系约束：

式中：αm,n为引水管Lm,n水头损失计算公式系数。

由式（4）—（9）所组成的数学模型（记为系统模型ModelM），虽然精确地描述了复杂引水电站系统负荷优化分配问题，但却十分复杂，难以直接应用传统成熟稳定的多阶段决策优化技术，即使采用现代各种智能算法，也存在判断决策可行性比较困难、且求解方法不具普适性的问题。

4 模型求解方法与等效机组（段）耗流量特性曲线及应用

4.1 模型求解方法基于以上水电站群系统聚合原理，ModelM可以通过从低级向高级的逐级子系统求解方法实现，任一层级（m）子系统的求解方法如下。

（2）优化求解等效机组最优耗流量特性曲线Nm,nHm,nQm,,n(n=1～Nm)。根据并联等效机组段构建相应的优化数学模型，优化求解即可得到等效机组的最优耗流量特性曲线、决策曲线及等效机组出力可行域。

遍历逐级子系统（m=1～M）即得到全站最优动力特性曲线。

基于以上分解聚合原理，这种构模方法及分层次递阶结构化模型求解方法，对于复杂水电站群系统具有很强的通用性，有助于编制大型面向对象的高性能结构化软件，同级子系统还可以应用并行计算等现代技术提高计算效率。

4.2 实例应用实例系统ModelM的求解过程如下。

（1）基于式（8g）和（9a），由各机组耗流量特性曲线N0,nH0,nQ0,n(n=1～N)，推求机组段耗流量特性曲线（ 实际应用中，该曲线不受优化模型影响，可以先制作好）。

（2）一级子系统优化（包括3个子模型），聚合U1,n(n=1～N1)。

①等效机组U1,1：在给定(H1,1,N1,1)条件下，以式（7b）最小为目标函数、式（6）相应机组为约束，形成子模型Model1,1。

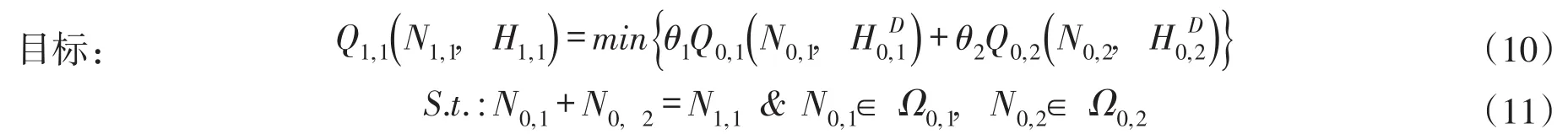
求解Model1,1即可得到N0,1、N0,2的最优决策及Q1,1的最优值，如果无解则说明给定的N1,1不可行（无法保证两台机组安全运行）。通过不同(H1,1,N1,1)组合求解Model1,1，则可以得到U1,1的最优耗流量曲线N1,1H1,1Q1,1、最优决策曲线N1,1H1,1N0,（2N0,1由式（11）计算）、以及可行出力范围Ω1,1。

②等效机组U1,2：在给定(H1,2,N1,2)条件下，以式（7c）最小为目标函数、式（6）相应机组为约束，形成子模型Model1,2：

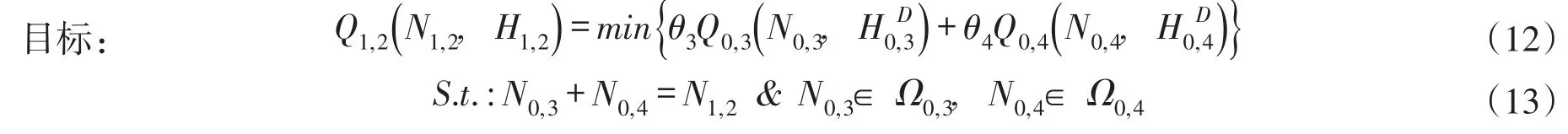
与Model1,1一样，反复求解Model1,2即得N1,2H1,2Q1,2、N1,2H1,2N0,4及Ω1,2。

③等效机组U1,3：U1,3属于串联等效机组（一般包含在一级子系统），串联机组引用流量相同、且上级电站尾水池水位Zlow和下级电站前池水位Zup不变，因此，不存在优化问题，且下级电站水头取决于水电站群尾水位Zxy、而上级电站水头则决定于H1,3和Zxy。在已知Zxy时，给定任一(H1,3,Q1,3)，下级机组段水头为，由和Q1,3查得N0,7；上级机组段水头为由和Q1,3查得N0,6，则N1,3=N0,6+N0,7；给定不同组合，即可得到给定Zxy下N1,3H1,3Q1,3和N1,3H1,3N0,6。给定不同Zxy，即可得相应的

（4）二级子系统优化。在给定(H2,1,N2,1)条件下，以式（7d）最小为目标函数、等效机组可行出力范围为约束，形成子模型Model2,1：

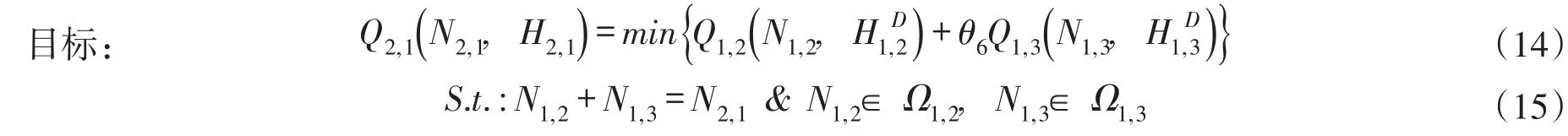
反复求解Model2,1即得由式（8i）、（9e），再求

（5）三级子系统优化。在给定(H3,1,N3,1)条件下，以式（7e）最小为目标函数、等效机组可行出力范围为约束，形成子模型Model3,1：

反复求解Model3,1即得及Ω3,1。由式（8j）、（9f），再推求

（6）四级子系统优化。在给定(H4,1,N4,1)条件下，以式（7f）最小为目标函数、等效机组可行出力范围为约束，形成模型Model4,（1即ModelM）：

反复求解Model4,1即得N4,1H4,1Q4,（1即NsdzHsdzQsdz）、N4,1H4,1N1,1及Ω4,1。

全部计算完成，停止计算。除U1,3外，其余子模型均可采用动态规划法求解，并形成静态特性曲线集合。实例水电站群求解过程如图3所示，全站最优流量特性曲线如图4所示。

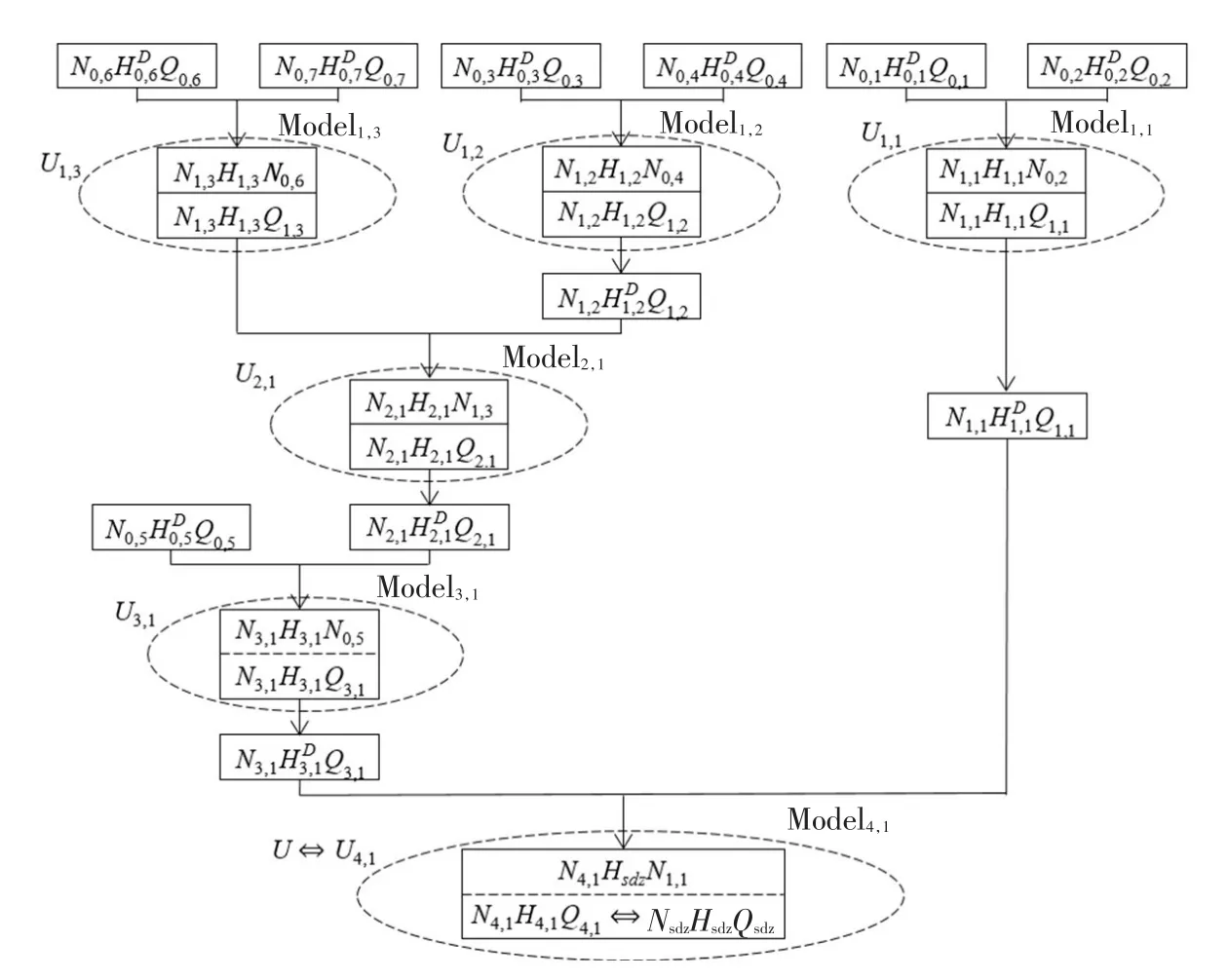
图3 漳河水库水电站群最优动力特性曲线绘制流程

图4 漳河水库水电站群最优流量特性曲线NsdzHsdzQsdz(Hsdz=50～61 m)

5 水电站负荷分配方法及应用

5.1 负荷分配方法水电站负荷分配主要包括以下三种情形。

（1）已知Hsdz和水电站尾水位Zxy（串联等效机组用）。对于“以电定水”方式已知Nsdz（“以水定电”方式可由Hsdz和Qsdz查NsdzHsdzQsdz得Nsdz），可以根据引水系统树状结构关系，形成实例系统的负荷分配流程图（如图5所示），通过逐层次子系统的分配，可得到各机组的出力和发电流量Q0,i。

（2）已知水库起始水位和入库流量，及全站时段平均发电流量Qsd（z“以水定电”）。可根据水量平衡关系推求水库平均水位、下游水位流量关系推求Zxy，二者相减即得Hsdz，再应用（1）即可。

图5 漳河水库电站群机组负荷分配流程

（3）已知水库起始水位和入库流量，及全站时段平均出力Nsd（z“以电定水”）。此时需要进行“简单”迭代计算，即假设总发电流量Q′sdz，计算Zxy和Hsdz，查NsdzHsdzQsdz得到相应最优出力N′sdz，如果N′sdz与Nsdz之间误差不满足精度要求，重新调整Q′sdz直至满足要求。迭代收敛后再应用（1）即可。

5.2 实例负荷分配对于漳河水电站群，以水头Hsdz=56m、Nsdz=2 000～8 000 kW为例，应用以上原理进行机组间负荷分配，其结果如表1所示（其中由于6号机组的流动尾水养殖虹鳟鱼，使得6号和7号机组不能停机，通过设置机组权重的方法实现优先分配）。由此可见，应用以上方法解决复杂引水系统水电站负荷分配问题变得十分简单、方便、直观和易于操作。

6 结论

本文应用分解聚合原理，提出了普适性的水电站负荷优化分配方法，经实例应用表明：（1）无论多么复杂的引水系统，通过绘制水力联系结构与动力指标要素图，以分流结点为依据进行系统分解，既可以简洁清晰地描述系统层次结构，又可建立全面完整的全站负荷分配优化数学模型。（2）以相同机组段水头（或流量）为依据，应用系统聚合原理，可将子系统内并（串）联机组段聚合成并（串）联“等效机组”；基于系统结构层次关系绘制“等效机组”聚合关系图，既明晰了不同层次“等效机组”的聚合关系，又实现了将总模型有机分解为不同层次的子模型、以便应用传统优化技术求解的目的。（3）在目标函数中赋予机组发电流量不同权重，可以处理机组投入顺序和检修需求，表明该方法具有优越的灵活性和实用性。（4）系统优化模型的构模方法及分层次递阶结构化模型求解方法，具有很强的通用性，有助于编制大型面向对象的高性能结构化软件，对于并行计算等现代技术解决大规模水电站群系统优化问题具有广阔的应用前景。

参 考 文 献：

［1］ HREINSSON E B.Optimal short term operation of a purely hydroelectric system［J］.IEEE Transactions on Power Systems，1988，3（3）：1072-1077.

［2］ 曾勇红，姜铁兵，张勇传.基于线性规划的梯级水电系统短期发电计划［J］.水电自动化与大坝监测，2004，28（4）：59-62.

［3］ WANG S J，SHAHIDEHPOUR S M，KIRSCHEN D S，et al.Short-term generation scheduling with transmission and environmental constraints using an augmented Lagrangian relaxation［J］.IEEE Transactions on Power Sys⁃tems，1995，10（3）：1294-1301.

［4］ FINARDI E C，SILVA E L D.Unit commitment of single hydroelectric plant［J］.Electric Power Systems Re⁃search，2005，75（2/3）：116-123.

［5］ CHANG G W，AGANAGIC M，WAIGHT J G，et al.Experiences with mixed integer linear programming based approaches on short-term hydro scheduling［J］.IEEE Transactions on Power Systems，2001，16（4）：743-749.

［6］ 梅亚东，左园忠，朱教新.一类含有0-1变量的厂内经济运行模型及解法［J］.水电能源科学，1999，17（3）：27-30.

［7］ 姚齐国，张士军，蒋传文，等.动态规划法在水电站厂内经济运行中的应用［J］.水电能源科学，1999，17（1）：46-49.

［8］ YI J，LABADIE J W，STITT S.Dynamic optimal unit commitment and loading in hydropower systems［J］.Jour⁃nal of Water Resources Planning&Management，2003，129（5）：388-398.

［9］ 程春田，唐子田，李刚，等.动态规划和粒子群算法在水电站厂内经济运行中的应用比较研究［J］.水力发电学报，2008（6）：27-31.

［10］ 蒋传文，权先璋，张勇传.水电站厂内经济运行中的一种混沌优化算法［J］.华中科技大学学报：自然科学版，1999（12）：39-40.

［11］ 王黎，马光文.基于遗传算法的水电站厂内经济运行新算法［J］.中国电机工程学报，1998（1）：65-67，9.

［12］ 李安强，王丽萍，蔺伟民，等.免疫粒子群算法在梯级电站短期优化调度中的应用［J］.水利学报，2008，39（4）：426-432.

［13］ 李崇浩，纪昌明，李文武.微粒群算法在水电站厂内经济运行中的应用研究［J］.水利水电技术，2006，37（1）：88-91.

［14］ 杨侃，陈垒，李浩.大型水电站整体时空经济运行模型及其算法［J］.华中科技大学学报：自然科学版，2015，43（9）：117-122.

［15］ 赵雪花，黄强，吴建华.蚁群算法在水电站厂内经济运行中的应用［J］.水力发电学报，2009，28（2）：139-142.

［16］ 王永强，周建中，覃晖，等.基于改进二进制粒子群与动态微增率逐次逼近法混合优化算法的水电站机组组合优化［J］.电力系统保护与控制，2011，39（10）：64-69.

［17］ 纪昌明，李继伟，张新明，等.梯级水电站短期发电优化调度的免疫蛙跳算法应用研究［J］.水力发电学报，2015，34（1）：29-36.

［18］ 原文林，吴泽宁，黄强，等.梯级水库短期发电优化调度的协进化粒子群算法应用研究［J］.系统工程理论与实践，2012，35（5）：1136-1142.