不同缝面形态下诱导缝开裂效果对比研究

李海枫，杨 波，张国新，徐秀鸣

（中国水利水电科学研究院 结构材料研究所，北京 100038）

1 研究背景

碾压混凝土拱坝中，横缝及诱导缝的缝面形式通常采用平面型、折面型及曲面型［1］。从空间形态来看，平面型诱导缝属于竖向垂直缝，折面型和曲面型可视为径向扭曲缝。一些采用径向扭曲缝的工程中，存在在坝体蓄水前诱导缝周边出现裂缝而诱导缝本身未张开的现象［2］，例如我国西南地区某碾压混凝土拱坝，诱导缝采用了径向扭缝设计，在蓄水前坝体出现了类似裂缝。针对这一现象，有研究人员提出径向扭曲缝不利于碾压混凝坝坝体沿诱导缝或横缝有规则张开，因此需要开展不同缝面形态下诱导缝开裂效果对比研究。

目前，诱导缝开裂试验研究主要集中在诱导板的削弱面积方面。曾昭扬等［3］提出的等效强度模型从结构层面上考虑诱导缝的开裂效应，该值大小不仅与材料本身有关，还与诱导缝形状、大小和布置有直接联系，但是等效强度表达式中并未考虑缝面空间形态的影响。另外，有学者基于断裂力学观点研究非共面诱导缝的布置问题［4］，并探讨了诱导缝斜向布置可行性，但是将非共面诱导缝开裂问题简化为水平面内和垂直于径向的铅垂面内的两个平面问题来考虑，该处理方式未能有效反映非共面诱导缝开裂问题的空间效应。诱导缝开裂问题，严格来讲是一个三维断裂问题。因此，需要从三维角度来分析不同空间缝面形式下诱导缝受力情况，研究不同缝面形式诱导缝结构的开裂效果。

根据碾压混凝土拱坝应力变化特点以及诱导缝开裂变化规律，本文拟定含不同缝面空间形态的有限大平板和圆筒拱坝算例，利用虚拟裂纹闭合法探讨不同荷载条件下缝面断裂参数变化规律，基于Richard脆性断裂准则［5］获取空间缝面等效应力强度因子，研究缝面应力强度因子随缝面夹角的变化规律；通过对归一化后的应力强度因子求倒数，获取不同缝面夹角条件下诱导缝等效强度的修正系数即缝面空间形态影响因子，以反映不同缝面空间形态下诱导缝开裂效果。

2 缝面断裂参数求解方法

2.1 面状裂纹的虚拟裂纹闭合法求解应力强度因子的方法［6］主要有基于裂缝尖端附近位移或应力的直接外推法，为提高求解精度，通常需要在裂尖布置奇异单元或叠折单元；另外就是采用裂缝尖端附近区域的等效区域积分如J积分、M积分等，或者采用虚拟裂纹闭合法［7～8］获取能量释放率，经变换得到应力强度因子。鉴于虚拟裂纹闭合法具有方法简单且精度可靠的优点，本文采用虚拟裂纹闭合方法来获取空间缝面的断裂参数。

对诱导缝而言，可将其视为一空间面状裂纹，虚拟裂纹扩展法计算应变能释放率公式为：

式中：GⅠ、GⅡ、和GⅢ分别为3种断裂形式的应变能释放率分量；∆A为实际裂纹尖端前缘沿虚拟裂纹扩展的面积；为实际裂纹尖端前沿虚拟裂纹扩展线上的应力分量；为虚拟裂纹尖端后部沿虚拟裂纹扩展线上的张开位移分量。

2.2 能量释放率与应力强度因子转换采用三维虚拟裂纹闭合法获取能量释放率后，可采用下式计算三维应力强度因子：

式中：KⅠ、KⅡ和KⅢ分别为3种断裂形式的应力强度因子；GⅠ、GⅡ和GⅢ分别为3种断裂形式的应变能释放率分量；E为材料的弹性模量；ν为材料的泊松比。

2.3 等效应力强度因子诱导缝开裂问题严格来讲是一个三维断裂问题，对于复合型（I+III、I+II、II+III、I+II+III型）断裂问题，由于其数学计算的复杂性及试验操作的困难，到目前为止仍然没有统一的理论准则。Pook准则［9］和Richard准则是近30年来最具影响力的三维复合型断裂准则，本文采用Richard准则来获取缝面等效应力强度因子Keff-Ⅰ,Ⅱ,Ⅲ。

Richard准则本质上是最大主应力准则，即σ′1准则，该准则认为裂纹沿垂直于最大主应力σ′1方向扩展。Richard准则拐折角φ0的表达式为：

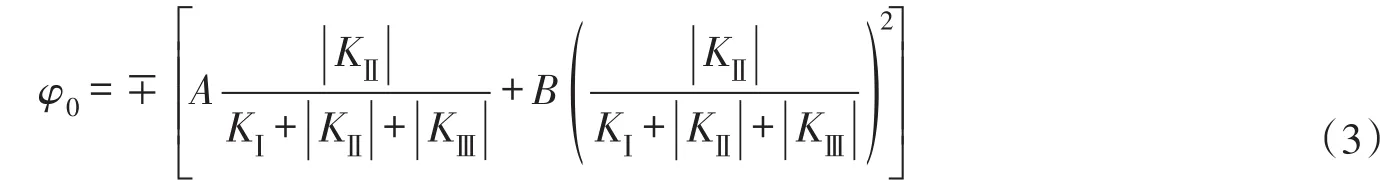
式中：KⅡ＞0时，ψ0＜0°；KⅢ＜0时，ψ0＞0°；A、B为计算系数，A=140°，B=-70°。

扭转角ψ0的表达式为：

式中：KⅡ＞0时，φ0＜0°；KⅡ＜0时，φ0＞0°；C、D为计算系数，C=78°，D=-33°。

Ⅰ+Ⅱ+Ⅲ复合型的等效应力强度因子Keff-Ⅰ,Ⅱ,Ⅲ的表达式为：

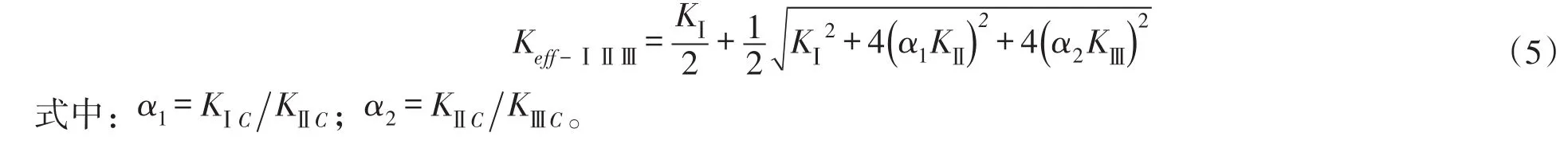
本文计算中，α1=1.155、α2=1.0。

3 不同空间形态缝面诱导缝开裂效果对比

3.1 有限大平板对比分析

3.1.1 计算模型 拟定一厚度为5 m、边长30 m×30 m的矩形板，板中轴线位置设置长3 m、间距3 m的一组穿透型诱导缝，缝与缝之间夹角θ按0°、5°、7.5°、10°、12.5°、15°、20°、25°及30°考虑，荷载作用矩形板左、右两侧，其荷载形式按轴拉和压剪两种情况来考虑。相应计算模型见图1。

3.1.2 结果分析

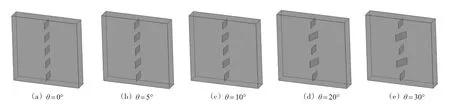
图1 有限大平板不同缝面夹角时诱导缝计算模型

（1）缝面应力强度因子变化规律。采用虚拟裂纹闭合法可以得到不同荷载作用下的缝面前缘各节点的能量释放率，经式（2）和式（5）转换可得缝面前缘各节点的等效应力强度因子。由压剪荷载作用下缝面前缘应力强度因子沿厚度方向分布曲线可知（图2、图3），随着直缝与扭缝之间夹角的逐渐增大，缝面前缘等效应力强度因子逐渐降低；其中，直缝等效应力强度因子变化很小，而扭缝等效应力强度因子降低较大。这主要是由于随着缝面夹角逐渐增大，直缝缝面前缘区域的应力边界条件基本不变化，而扭缝缝面的边界条件则发生较大变化，导致扭缝缝面前缘局部应力汇聚的密集程度产生较大变化，直缝缝面前缘局部应力则基本不变化；由于应力强度因子是表征裂缝尖端弹性应力场强弱的物理量，因此随着缝面夹角增大，直缝应力强度因子基本不变化，而扭缝的变化较大。

（2）不同缝面夹角条件下缝面应力强度因子变化规律。为便于对不同缝面夹角下缝面应力强度因子进行对比分析，故将缝面前缘等效应力强度因子作平均化处理（表1）。从表1可以看出，随着缝面夹角增大，缝面平均等效应力强度因子也随之减小，并且剪切荷载作用下的减小趋势要大于轴拉荷载作用。

图2 不同缝面夹角下压剪荷载时直缝缝面前缘应力强度因子沿板厚方向分布曲线

图3 不同缝面夹角下压剪荷载时扭缝缝面前缘应力强度因子沿板厚方向分布曲线

为便于研究缝面应力强度因子随缝面夹角的变化趋势，故以直缝与扭缝夹角取0°时作为基准，进行不同缝面夹角条件下缝面平均等效应力强度因子归一化处理（表2），其变化曲线见图4—图5。对比图4与图5可知，随着缝面夹角增大，直缝缝面的等效应力强度因子基本不变，扭缝缝面应力强度因子减小比较明显。轴拉荷载下，缝面夹角增大至25°时，扭缝缝面应力强度因子才降低2%。而压剪荷载下，当缝面夹角为5°时，扭缝缝面应力强度因子减低2%；缝面夹角增大至10°时，应力强度因子降低4.3%；夹角增大至15°时，应力强度因子降低7.5%；夹角增大至25°时，应力强度因子降低16%；夹角增大至30°时，应力强度因子降低21%。综合来看，随着缝面夹角增大，缝面应力强度因子均呈不同程度降低，扭缝降低程度要明显大于直缝。当缝面夹角为10°时，应力强度因子最大降低4.3%；当缝面夹角为20°时，应力强度因子最大降低11.4%；当缝面夹角为25°时，应力强度因子最大降低16%；当缝面夹角为30°时，应力强度因子最大降低21%。

3.2 圆筒拱坝对比分析

表1 有限大平板不同缝面夹角下裂缝前沿平均等效应力强度因子

表2 归一化处理的有限大平板不同缝面夹角下裂缝前沿平均等效应力强度因子

图4 轴拉荷载下裂缝前缘平均等效应力强度因子随缝面夹角变化曲线

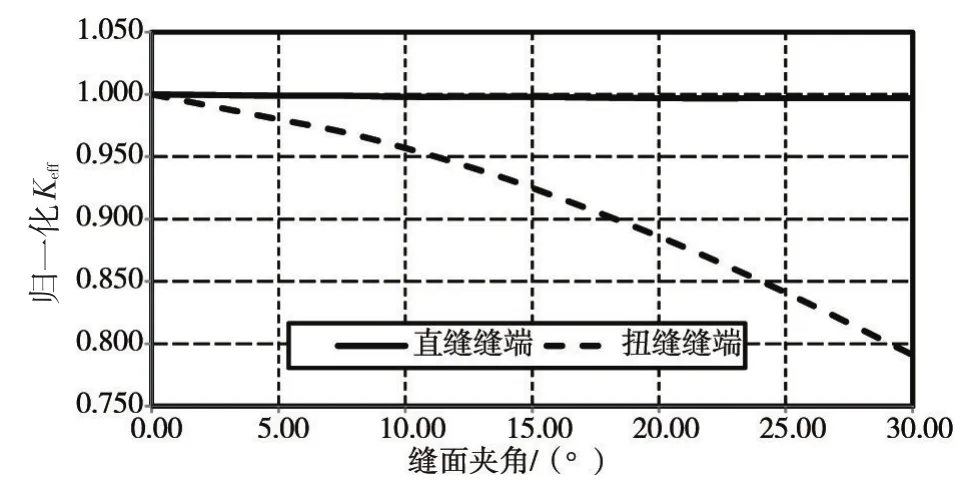
图5 压剪荷载下裂缝前缘平均等效应力强度因子随缝面夹角变化曲线

3.2.1 计算模型 对于碾压混凝土拱坝而言，诱导缝通常设置在岸坡坝段。对于诱导缝而言，应主要考虑拱坝第一次蓄水前的空库应力状态。这是因为建成蓄水前，拱坝在施工温降作用下普遍受拉状态，有利于诱导缝的拉开，这也是诱导缝发挥作用的最佳时期。如果蓄水前诱导缝没有张开，蓄水后由于上游水荷载的作用拱坝普遍处于受压状态，诱导缝就很难张开并发挥作用［10］。

根据以上分析，拟定一厚度为5 m、内径60 m、外径65 m、高27 m。半中心角为45°的半圆筒拱坝模型，并考虑岸坡影响，该模型展开后为一梯形形式，坡角考虑30°、45°和60°。在距底边1/3处的岸坡边上部设置长3 m、间距3 m的一组穿透型诱导缝，缝与缝之间夹角θ按0°、5°、7.5°、10°、12.5°、15°、20°、25°及30°考虑。模型见图6。荷载考虑温降荷载，按5°降温考虑。半圆筒拱坝两侧施加约束，左侧即岸坡侧按全约束施加，右侧按对称约束施加。

3.2.2 结果分析 为便于对不同缝面夹角下缝面应力强度因子进行对比分析，故将缝面前缘等效应力强度因子作平均化处理（表3）。从表3可见，随着缝面夹角增大，缝面平均等效应力强度因子也随之减小。为便于研究缝面应力强度因子随缝面夹角的变化趋势，故以直缝与扭缝夹角取0°时作为基准，进行不同缝面夹角条件下缝面平均等效应力强度因子归一化处理（表4），其变化曲线见图7—图9。

由图7—图9可以发现，随着缝面夹角增大，扭缝缝面应力强度因子减小较直缝缝面明显。（1）坡角30°时，当缝面夹角增大至5°时，直缝和扭缝的缝面应力强度因子降低1%；夹角增大至10°时，缝面应力强度因子降低2%；夹角增大至20°时，直缝应力强度因子降低2.5%，扭缝应力强度因子降低5%；夹角增大至25°时，直缝降低3%，扭缝降低8.5%；夹角增大至30°时，直缝降低3.5%，扭缝降低14%。（2）坡角增大至45°时，缝面夹角为5°时，直缝维持不变，而扭缝降低1.5%；夹角为10°时，直缝降低1.5%，扭缝降低3.3%；夹角为15°时，直缝降低2%，扭缝降低5%；夹角为20°时，直缝降低2%，扭缝降低8%；夹角为25°时，直缝降低2.3%，扭缝降低11%；夹角为30°时，直缝降低5.7%，扭缝降低15%。（3）坡角增大至60°时，缝面夹角为10°时，直缝基本维持不变，而扭缝降低2%；夹角为15°时，直缝降低7%，扭缝降低5%；夹角为20°时，直缝降低7.5%，扭缝降低7%；夹角为25°时，直缝降低8.4%，扭缝降低12%；夹角为30°时，直缝降低9%，扭缝降低17%。

图6 圆筒拱坝不同缝面夹角时诱导缝（坡角为45°）

表3 圆筒拱坝不同缝面夹角下裂缝前沿平均等效应力强度因子

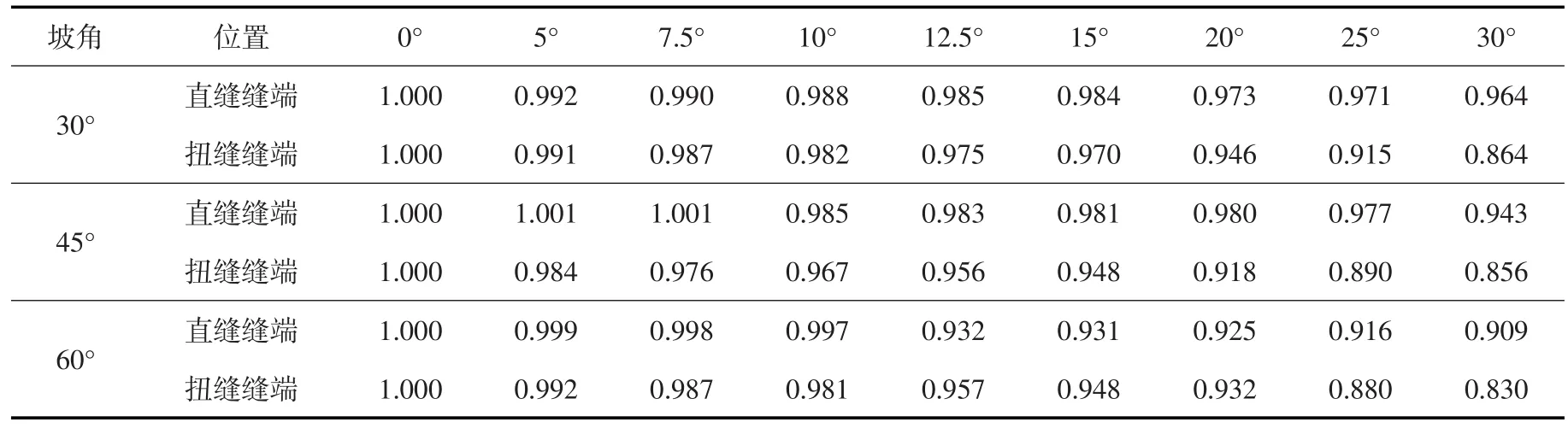
表4 归一化后的圆筒拱坝不同缝面夹角下裂缝前沿平均等效应力强度因子

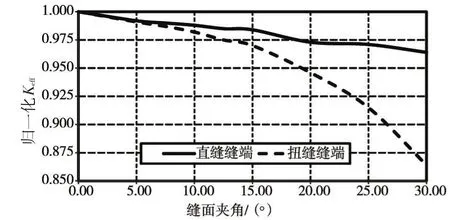
图7 坡角30°时裂缝前缘平均等效应力强度因子随缝面夹角变化曲线

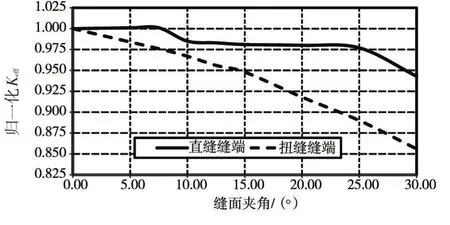
图8 坡角45°时裂缝前缘平均等效应力强度因子随缝面夹角变化曲线

综合来看，随着缝面夹角增大，缝面应力强度因子均呈不同程度降低，扭缝降低程度要明显大于直缝；当缝面夹角为10°时，应力强度因子最大降低3%；当缝面夹角为20°时，应力强度因子最大降低8%；当缝面夹角为25°时，应力强度因子最大降低12%；当缝面夹角为30°时，应力强度因子最大降低17%。

图9 坡角60°时裂缝前缘平均等效应力强度因子随缝面夹角变化曲线

4 现有诱导缝等效强度模型讨论及修正

为研究诱导缝开裂破坏及其合理布置问题，清华大学曾昭扬教授在“八五”及“九五”攻关期间，将诱导缝简化为无限大板穿透模型和无限大体深埋椭圆裂缝模型，根据断裂力学理论提出了诱导缝的等效强度模型（见图10）。张小刚［11］研究认为，这两种计算模型得到的诱导缝等效强度相差不大。由于无限大体深埋椭圆裂缝模型能够同时考虑相邻诱导缝短轴方向的影响及远场应力和诱导缝短轴有效裂缝长度这两个因素，目前，诱导缝等效强度计算公式大都采用基于无限大体深埋椭圆裂缝的诱导缝等效强度计算模型，如下式：

图10 诱导缝计算模型

式中：KIC为混凝土的断裂韧度；λ为修正系数，反映了相邻预留子缝之间的相互作用；r0为混凝土应变软化区尺寸有关的参数；Φ为第二椭圆积分；a、b、c为图10所示的预留子缝尺寸与间距。

黄达海等［12］、张小刚等［13］、刘海成等［14］、黄志强等［15］和王学志等［16］基于混凝土双 K断裂理论［17］，开展不同工况下的诱导缝断裂破坏试验，从诱导板类型、试件尺寸效应、边界效应、裂纹有效扩展量以及混凝土名义断裂韧度等方面对诱导缝等效强度理论进行修正，但上述对诱导缝等效强度模型的修正并未考虑缝面空间形态的影响。综合有限大平板与圆筒拱坝的分析成果可知，随着缝面夹角的增大，缝面应力强度因子均呈不同程度降低，扭缝降低程度要明显大于直缝。现将不同工况下归一化后的缝面应力强度因子列于表5中的（1）—（5）列，取前（5）列应力强度因子的最小值作为第（6）列。由第（6）列数据可知，当缝面夹角为5°时，缝面应力强度因子降至0.98；当夹角为10°时，应力强度因子降至0.957；夹角为15°时，降至0.925；夹角为20°时，降至0.886；夹角为30°时，降至0.791。

从诱导缝等效强度理论角度来看，随着缝面夹角的不断增大，缝面越不容易张开，这就意味着缝面的等效强度在逐渐增大。因此，可对归一化的应力强度因子求倒数，将其作为不同缝面夹角条件下诱导缝等效强度的修正系数，这里简称缝面空间形态影响因子λ（θ）。

将表5中的第6列的归一化应力强度因子求倒数，作为缝面空间形态影响因子，并列于表5中。由不同缝面夹角下缝面空间形态影响因子分布曲线可知（图11），随着缝面夹角不断增大，扭缝缝面的等效强度也在逐渐增大；当夹角为5°时，缝面空间形态影响因子为1.02，这意味着诱导缝等效强度增大2%；夹角为10°时，等效强度增大4%；夹角为15°时，等效强度增大8%；夹角为20°时，等效强度增大13%；夹角为30°时，等效强度增大26%。为便于设计使用，对不同缝面夹角下缝面空间形态影响因子进行回归拟合，可得到拟合公式：

式中：λ（θ）为缝面空间形态影响因子；θ为诱导缝缝面夹角。

拟合公式的相关系数为0.9995。

根据以上分析，可以在已有的诱导缝等效强度模型基础上，增加缝面空间形态影响因子一项，以反映缝面形态对等效强度的影响，具体见下式：

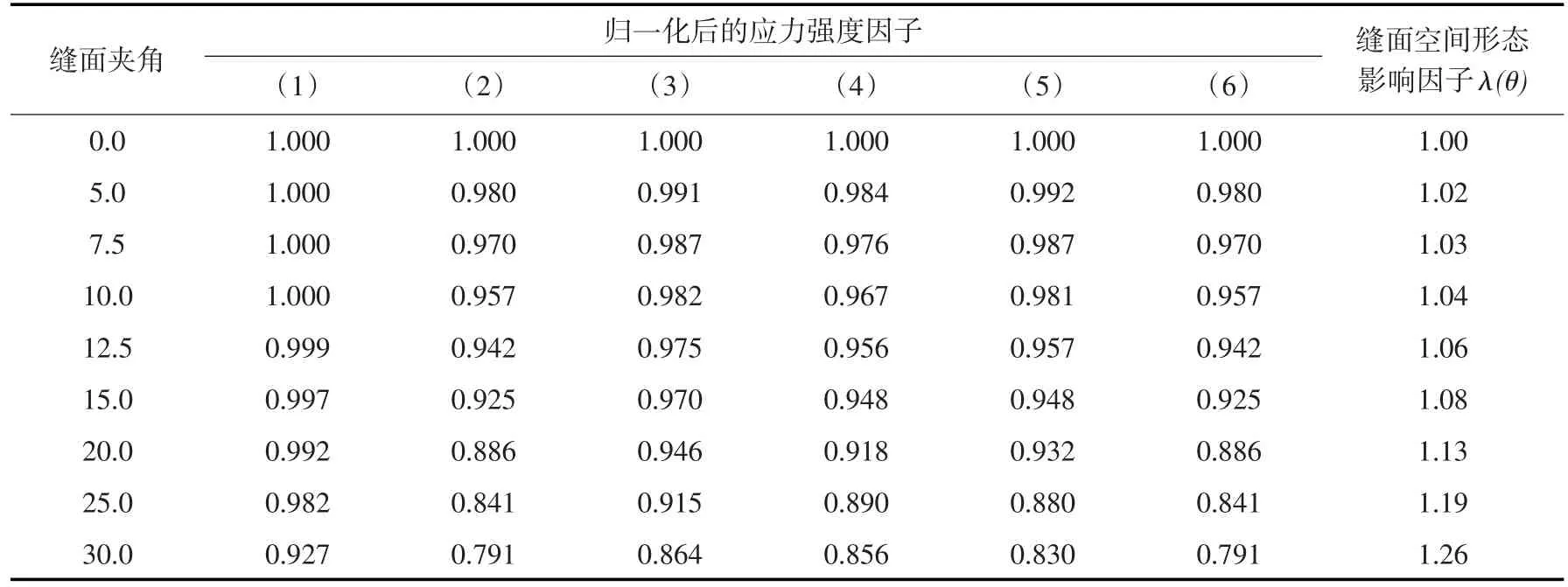
表5 不同缝面夹角下缝面应力强度因子及缝面空间形态影响因子

图11 不同缝面夹角下的缝面空间形态影响因子

5 结论

经计算分析，可得出以下结论：（1）随着缝面夹角增大，缝面应力强度因子均呈不同程度降低，扭缝降低程度要明显大于直缝。当缝面夹角为10°时，应力强度因子最大降低4.3%；当缝面夹角为20°时，应力强度因子最大降低11.4%；当缝面夹角为25°时，应力强度因子最大降低16%；当缝面夹角为30°时，应力强度因子最大降低21%。（2）从诱导缝等效强度理论角度来看，随着缝面夹角的不断增大，缝面越不容易张开，这就意味着缝面的等效强度在逐渐增大；将归一化的应力强度因子求倒数作为不同缝面夹角条件下诱导缝等效强度的修正系数，即缝面空间形态影响因子λ（θ），以反映不同缝面形态对诱导缝等效强度的影响。（3）随着缝面夹角不断增大，扭缝缝面的等效强度也在逐渐增大，因此，可在已有诱导缝等效强度模型即式（6）基础上，增加缝面空间形态影响因子一项，以反映缝面形态对等效强度的影响，即式（8）。（4）当缝面夹角超过10°时，诱导缝等效强度将增大4%以上，增加了诱导缝张开难度，并且即使张开也会导致缝面凹凸不平影响接缝灌浆质量；另外由于碾压混凝土是薄层碾压，布置预制块相邻拱圈径向夹角超过10°的可能性极小。因此，实际碾压混凝土拱坝设计中，诱导缝应尽量采用竖向垂直缝布置，若要布置成径向扭缝，缝面夹角最大不宜超过10°。

参 考 文 献：

［1］ 范福平，龙起煌，罗洪波，等.峡谷地区碾压混凝土筑坝技术与实践［M］.北京：中国水利水电出版社，2015.

［2］ 崔进，陈毅峰，谭建军.碾压混凝土高拱坝防裂技术综述［C］//中国大坝协会2014学术年会.2014.

［3］ 曾昭扬，马黔.高碾压混凝土拱坝中的构造缝问题研究［J］.水力发电，1998（2）：30-33.

［4］ 顾爱军，朱为玄，王向东，等.碾压混凝土拱坝诱导缝的断裂力学分析［J］.红水河，2004，23（1）：21-24.

［5］ SCHÖLLMANN M，RICHARD H A，KULLMER G，et al.A new criterion for the prediction of crack develop⁃ment in multiaxially loaded structures［J］.International Journal of Fracture，2002，117（2）：129-141.

［6］ 解德，钱勤，李长安.断裂力学中的数值计算方法及工程应用［M］.北京：科学出版社，2009.

［7］ RYBICKI E F，KANNINEN M F.A finite element calculation of stress intensity factors by a modified crack clo⁃sure integral［J］.Engineering Fracture Mechanics，1977，9（4）：931-938.

［8］ SHIVAKUMAR K N，TAN P W，JR J C N.A virtual crack-closure technique for calculating stress intensity fac⁃tors for cracked three dimensional bodies［J］.International Journal of Fracture，1988，36（3）：43-50.

［9］ POOK L P.Linear Elastic Fracture Mechanics for Engineers：Theory Andapplication［M］.Southampton：WIT Press，2000.

［10］ 张国新，杨波，张景华.RCC拱坝的封拱温度与温度荷载研究［J］.水利学报，2011，42（7）：812-818.

［11］ 张小刚.碾压混凝土诱导缝断面强度、断裂的试验研究和数值模拟［D］.大连：大连理工大学，2005.

［12］ 黄达海，宋玉普，赵国藩.碾压混凝土拱坝诱导缝的等效强度研究［J］.工程力学，2000，17（3）：16-17.

［13］ 张小刚，宋玉普，王学志，等.碾压混凝土拱坝诱导缝等效强度双参数断裂模型［J］.大连理工大学学报，2005，45（2）：265-271.

［14］ 刘海成，宋玉普，姚国军，等.沙牌碾压混凝土拱坝诱导缝开裂研究［J］.大连理工大学学报，2004，44（1）：104-109.

［15］ 黄志强，王学志，沈新普，等.碾压混凝土拱坝双向相邻诱导缝断裂试验与分析［J］.水利学报，2010，41（2）：198-204.

［16］ 王学志，宋玉普，张小刚，等.碾压混凝土拱坝双向间隔诱导缝等效强度研究［J］.大连理工大学学报，2006，46（2）：252-256.

［17］ 徐世烺.混凝土断裂力学［M］.北京：科学出版社，2011.