基于神经网络理论的开河期冰坝预报研究

王 涛，刘之平，郭新蕾，付 辉，刘文斌

（1.中国水利水电科学研究院 流域水循环与调控国家重点实验室，北京 100038；2.黑龙江省水文局，黑龙江 哈尔滨 150001）

1 研究背景

冰坝和冰塞是寒冷地区江河中较常出现的冰情现象，易导致凌汛洪水灾害。在1986年召开的国际水利和环境工程学会（IAHR）冰工程分会上明确了冰塞和冰坝的概念［1］：冰塞为封河期大量冰花不断下潜在冰盖下受阻堆积所形成的冰情现象；冰坝为水面上大量流冰块遇到下游冰盖阻碍堆积导致河道堵塞和水面雍高的现象，在开河和封河期都会发生。封河期冰塞和冰坝形成机理的热力学和动力学机理相对明确，其形成可通过数学模型进行模拟和预报。Shen［2-3］开发了冰花堆积和输移的一维和二维模型，模拟天然河道冰塞堆积过程，并开展了流冰期和冰盖形成过程的模拟和预报［4］。杨开林等［5-6］开发冰塞堆积的一维数学模型，模拟了松花江流域白山河段冰盖的发展过程。王军等［7-9］采用数值计算和物理模型试验模拟封河期冰塞的堆积过程。茅泽育等［10］建立了冰塞演变的冰水耦合综合动态数学模型，模拟黄河河曲段冰塞发展和水位演变的规律。郭新蕾等［11-12］采用一维树状数学模型模拟调水工程等人工渠道冰盖发展过程。Beltaos［13］和Fuhui［14-15］给出了渠道倒虹吸形成冰塞下潜条件的判别式。然而，通过建立数学模型开展冰过程模拟，对实测资料精度要求高，特别是要求有河道河床资料作为计算必要的边界条件。但如我国最北端的黑龙江属于中俄界河，河道测量只能在中方边界内，目前尚未有完整的河床断面资料，数学模型的应用受到限制。再如黄河作为游荡型河道，河床主槽位置容易冲刷改变，新建的数学模型在河道断面改变的情况下将无法继续使用。人工神经网络模型能够克服冰情预报中河道实测资料不全或缺失、河道断面资料难以测量等条件制约。陈守煜等［16］提出把传统的BP神经网络算法应用到冬季流凌和封河预报中。王涛等［17-18］采用神经模糊理论模型开展天然河道及调水明渠流凌和封河时间的预报，并在黄河和南水北调中线工程中得到应用。

开河分为文开河和武开河。文开河为在热力作用下，冰盖慢慢消融的过程，无明显大块浮冰在下游冰盖上堆积，通常也不会产生冰坝；武开河是在水力和热力共同作用下的机械开河，开河前冰内部结构疏松，冰盖强度降低，岸边的积雪融水和降雪（雨）导致冰盖上承载负荷增加，当水流动力、上游来冰作用力和冰盖上负荷等作用力超过冰盖承载能力的时候，冰盖破裂。破碎的冰块向下游输送，遇到下游冰盖或者河道阻挡时，导致冰块堆积形成冰坝。冰坝阻挡水流下泄，引发水面快速雍高，可造成洪水灾害；当冰坝突然溃决，也会出现溃坝洪水灾害。因此准确的冰坝预报能为开展冰坝预警、提前采取措施预防冰坝发生或缓解冰坝造成的洪水灾害赢得足够时间。但开河期冰坝形成和发展过程是复杂的水文、气象、水力、热力和动力等因素交互作用的结果，由于其形成过程的影响因素复杂，目前很少有数学模型能完成开河期冰坝的预报及模拟。现有的开河期冰坝开展研究较多的为加拿大Beltos［19-21］，描述和分析了开河期冰块堆积、冰坝形成、冰坝破坏的物理过程，并提出当水位上升超过封河水位，且超出高度与冬末冰厚成一定比例时，就会发生冰盖破裂或者流冰，这一特定的临界标准为经验数值。戴长雷等［22］借鉴苏联在冰坝预报方面的研究成果，采用统计学方法和经验公式预报黑龙江冰坝发生与否。王涛等［23-25］采用神经网络理论预报黄河开河日期和冬季水温变化过程。Mahabir［26-27］采用神经模糊推理系统预报Athabasca河开河日期和开河期冰坝洪水过程。综上所述，神经网络模糊理论已经应用到开河日期的预报，但对冰坝形成要素的预报仍建立在经验判别法和统计学方法基础上，亟待找到新方法、建立新模型开展冰坝的预报。

本文在对开河期冰坝成因及机理研究的基础上，建立基于Levenberg-Marquart算法的Back Propa⁃gation（BP）神经网络冰坝预报模型，采用神经聚类法预报开河期冰坝发生情况，并将其应用到黑龙江上游凌汛灾害频发的漠河江段冰坝预报中。

2 冰坝预报的神经网络模型

建立在BP神经网络理论基础上的冰情预报模型分为网络的历史冰情学习过程和网络的预报过程，如图1所示。网络的学习过程可分为信息的正向传递和权重的逆向修正2个过程：输入的信息流从输入层经隐层到输出层，这一过程称为信息的正向传递过程；若网络的实际输出与训练样本期望值的误差未达到允许值，根据此误差从后往前逐层传递修改各层神经元节点的连接权重，这一过程称为权重的逆向修正过程。这2个过程不断迭代，直到网络的输出误差达到允许的精度，或达到设定的学习次数，网络学习过程结束，根据网络对历史数据的学习得到的权重开展冰坝预报。经典的BP神经网络建立在梯度下降法基础上，但是在冰情预报过程中发现，网络逼近非常慢，且通常逼近误差达不到理论值时，就陷入局部最小，导致网络无法学习下去。鉴于此，采用Levenberg-Marquart算法改进BP神经网络模型开展冰坝预报，Levenberg-Marquart算法是用平方误差代替均方误差，使误差平方和最小。该算法同时具有牛顿法和梯度下降法两者的优势，实践证明Levenberg-Marquart算法比梯度下降法收敛速度更快［23］。

图1 BP神经网络训练过程

建立在对水文、气象和观测的冰情数据学习基础上的冰坝预报神经网络模型，预报冰坝发生情况，输出为发生冰坝和不发生冰坝（对应的网络输出分别为1和0）。网络训练和输出过程就是网络聚类过程，即将属性相似的集合划分为一类。因为神经网络学习和计算过程为非线性过程，图2为显示一个非线性边界比一个线性边界更好实现非线性问题的分类。通过神经网络聚类的非线性学习和计算过程，完成冰坝发生情况的预报。开河期冰坝通常发生在河道开河期间，通过预报开河日期实现冰坝发生时间的预报。

图2 线性和非线性边界对网络分类的影响

建立在开河期冰坝预报因子基础上的冰坝预报模型表达为：

式中：Djam为冰坝发生情况；Pbf为封江前降雨量，mm；Pdf为封江期降雨量，mm；Pbb为开河前期降雨量，mm；Tdf为封江期累计负气温和，℃；Tbb为开河前期气温变化，℃；Q为流量，m3/s；Hl为封河水位，m；Hice为冰盖厚度，m；Hsnow为冰盖上积雪厚度，m；Vcs为槽蓄量，m3。

为了消除网络学习和预报中各个因子由于量纲和单位不同带来的影响，以及防止部分神经元达到饱和状态，对样本进行无量纲的规格化处理：

式中：zi和yi分别为转换前后的变量；zmax和zmin分别为zi的最大值和最小值；α取值为0和1之间的参数；这样确保得到的输入量yi在［0、1］区间内。

3 黑龙江冰坝的成因及预报模型

黑龙江位于我国最北端，地理位置特别为中俄界河，冰盖厚度可达2.0 m且坚固，冰面覆盖平均厚度可达30 cm的积雪。从20世纪50年代以来统计资料表明：黑龙江局部河段卡塞几乎年年发生，平均3年左右形成一次具有一定规模的冰坝。历史上发生冰坝情况如表1所示，1950年以来的67年间，严重冰坝发生10次，其中1960年和1985年为特大冰坝，最大雍高水头分别达到13.56 m和12.60 m，所以黑龙江凌汛灾害非常严重。但黑龙江在冰坝的观测、预报、防治的研究方面一直处于相对落后状态。做好黑龙江开河期冰坝的预报，为提前实施冰坝破除和冰灾的预防提供可靠的科技支撑。表1表明，黑龙江冰坝一般发生在开河期间，地点主要集中在上游的漠河江段，形成冰坝的主要原因如下。

（1）地理位置与河流流向影响。地理位置和河流流向是造成倒开河形成冰坝的主要条件。黑龙江上游额尔古纳河和石勒喀河2大支流从西南流向东北（如图3所示），由低纬度向高纬度流动，纬度相差7度，纬距700 km，使源头和支流开河早于干流，造成冰块堆积，壅冰成坝，倒开河为冰坝形成准备了先决条件。

（2）地形与河道形态特征。地形与河道形态特征是冰坝形成的重要边界条件。黑龙江上游流经山区，两岸高山、峡谷、平原相间。同一太阳辐射热力条件下，平原受热大于峡谷，朝阳面大于山脉遮挡的背阴面，造成不同河段冰层解冻程度不同，沿途节节卡冰形成结坝。黑龙江上游属于典型的山区性河流，河道坡降变化急剧，河谷宽窄相间，岸线极不规则，江道呈L型、S型或Ω型，甚至出现大于90度转折。部分段江道狭窄曲折，局部岛屿相连，分岔和串沟较多，河槽宽窄及深浅变化相差悬殊，河道形态特征及过水能力均具备形成冰坝的水力条件。

（3）水文气象因素。水文气象因素是形成冰坝的直接原因。影响黑龙江冰坝形成的水文和气象因素主要包括：流域冬春气温、河槽蓄水蓄冰量、封冻期降雪（水）量、蒸发量、冬季气温、流冰密度及流冰尺寸等。体现在具体水文信息上为：槽蓄量、封江水位、11月—翌年3月的降雨量、开河前4月降雨量、封冻期气温、开河前气温变化和冰盖厚度等。这些因素出现极端或者不利工况，会造成黑龙江武开河，为冰坝形成创造有利条件。

表1 黑龙江冰坝发生情况

图3 黑龙江河流位置和流向

黑龙江地处偏远，交通、通讯、观测设备和测量手段落后，水文站的数量远远低于国内平均水平，黑龙江作为中俄界河，河道断面和流量等要素不能直接测量，以上因素导致预报所需的水文、气象和河道数据严重不足，在冰坝预报中可以利用的水文数据主要是10月到翌年4月的降雨量。本研究采用神经网络模型预报黑龙江上游漠河江段的冰坝发生情况，模型所需要的水文资料主要来自漠河县北极乡水位站，日降雪（雨）量和日均气温资料来自国家气象局漠河县资料，预报因子包括：封江前降雨（雪）量，mm；封冻期降雨（雪）量，mm；开河前降雨（雪）量，mm；封江期累计负气温，℃；开河前期气温变化，℃；冰盖厚度，m；气温稳定转正日期，月/日。

4 冰坝发生情况预报

基于Levenberg-Marquart算法改进的BP神经网络聚类法预报黑龙江冰坝发生情况，采用3层网络结构：即输入层、隐层和输出层各1个，Sigmoid函数作为隐层的隶属函数，为了使网络输出固定在0～1之间，Logarithm函数被应用作为输出层的隶属函数。在网络训练中学习率在0～1之间变化。1957—2002年水文和气象数据作为网络的学习值，2003—2015年数据作为网络的预报值，预报结果如表2所示。

表2 神经网络聚类法和几率发生率法预报冰坝发生情况的比较

为了比较神经网络模型预报效果，采用经验统计法预报结果进行对比。黑龙江冰坝预报目前采用的经验统计学模型为几率统计法，发生率P可表示为

式中：n为影响因子个数；Pn为第n个影响因子的几率；Ptotal为影响因子的几率和；Paverage为n个影响因子的平均几率。

研究了1990—2015年冰坝因子发生率，因子平均发生率均值为45%，故以45%作为标准判断冰坝是否发生的依据。表2为神经网络聚类法和几率发生率法预报冰坝发生情况的比较。预报2003—2015年13年冰坝发生情况，神经网络聚类法预报错误2年，统计学方法预报错误5年，神经网络聚类法预报精度为85%，统计学模型预报精度62%，神经网络聚类法预报冰坝明显优于传统统计学预报方法。2015年2种方法都预报冰坝的发生，因为2015年封江期和开河期的降雨量分别超过多年平均51%和74%，为冰坝发生创造有利条件。但2015年开河前根据提前预报的冰坝情况，在黑龙江上游漠河冰坝潜在发生江段实施了防凌爆破措施，阻止了冰坝发生，确保了该年度黑龙江上游顺利开河，未发生因冰坝洪水造成的凌汛灾害。

5 开河日期预报

开河期冰坝主要发生在开河后1～2 d，通过预报开河日期，预知冰坝发生的时间，能为冰坝和冰坝造成洪水灾害预防或提前采取措施赢得宝贵时间。采用Levenberg-Marquart算法改进的BP神经网络进行漠河开河日期预报，1957—2003年资料作为神经网络的学习数据，预报2004—2015年开河日期，预报结果见表3所示。预报12年开河日期，平均预见期10 d，最大误差2 d。根据《水文情报预报规范》（（GB/T 22482-2008））预报结果均合格。

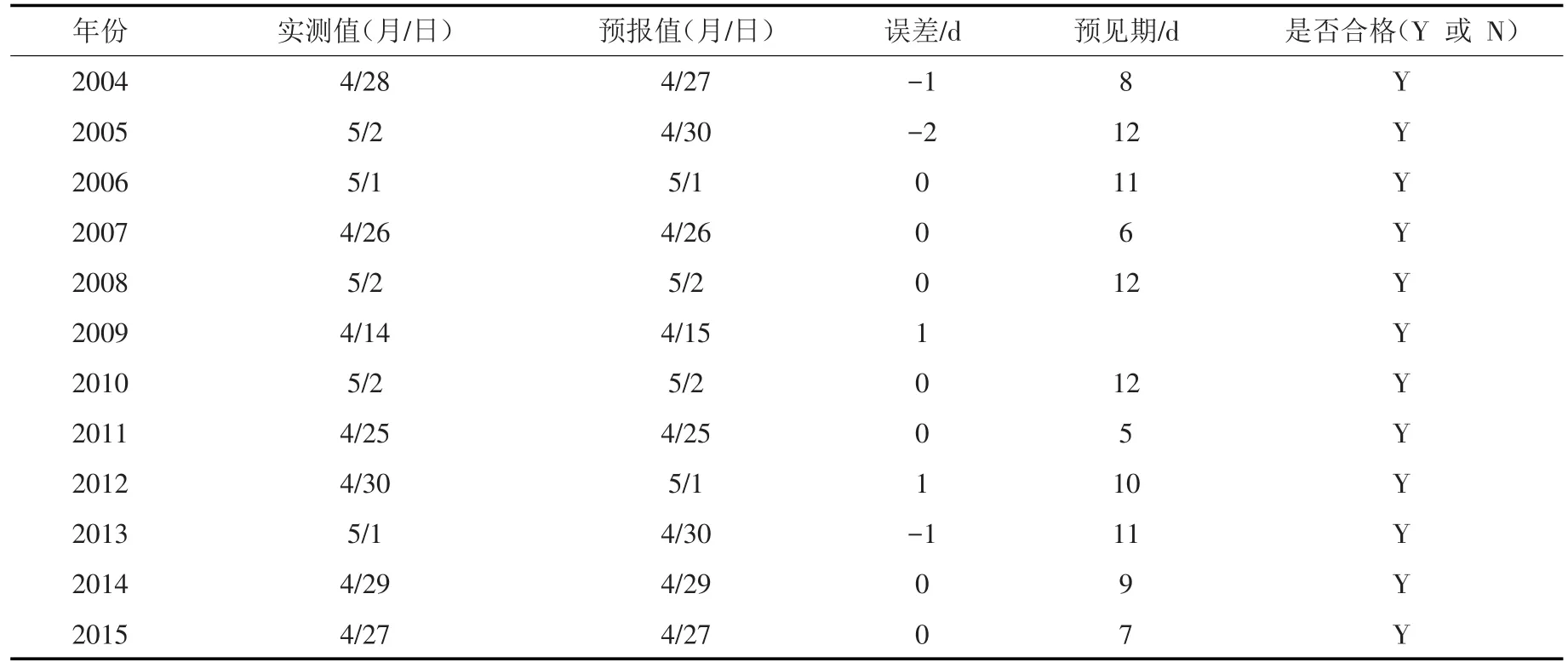
表3 开河预报结果

6 结论

北方高寒地区开河期冰坝造成的凌汛灾害严重，对冰坝发生可能性和发生时间进行预测和分析，是实施防凌减灾的前提和关键。开河期冰坝形成和发展过程影响因素复杂，冰坝形成和溃决速度快，观测和测量困难，预报难度很大。人工神经网络具有如下特点：对复杂非线性映射关系的强大逼近能力、对信息处理的良好的鲁棒性和容错性、对含糊和不完整等信息处理的强适应能力等，因此能够应用到冰坝预报这种受多种因子影响而很难找到一个确切相关关系的复杂非线性问题中。本文建立了北方寒冷地区天然河道神经网络的冰坝预报模型，结论如下：（1）通过黑龙江历史冰坝调查分析和理论研究，将黑龙江冰坝形成的主要原因概括为河道特征、动力因素和热力因素。通过冰坝成因分析并结合当前水文、气象资料现状，确定了开河和冰坝预报因子为：封河前降雨量、封河期间降雪（雨）量、春季开河前期降雪（雨）量、封河期气温、开河前期气温变化、开河前期水位变化和冰厚等。（2）基于神经网络聚类的冰坝预报模型应用到黑龙江漠河江段冰坝预报中，通过神经网路的自学习将冰坝发生情况的属性进行聚类，完成了冰坝发生或不发生情况的预报，并同统计学方法预报结果进行比较。预报2003—2015年共13年冰坝发生情况，神经网络聚类法预报精度为85%，统计学模型预报精度为62%，神经网络聚类法明显优于传统统计学预报方法。（3）通过神经网络模型预报漠河开河日期，实现冰坝发生时间的预报。预报2004—2015年12年开河日期，最大误差2 d，平均预见期10 d，预报结果全部合格。

本预报模型应用到2017年黑龙江上游漠河江段冰情预报中，在4月1日预报出本年度开河期将不发生冰坝灾害，预报开河日期为4月28日。实测黑龙江源头洛古河江段开江日期为4月28日，漠河北极乡江段开河日期为4月24日，未发生冰坝造成的凌汛灾害。洛古河开河日期同预报值同天，北极乡在开河前（4月9—12日）实施开江前预防性的防凌爆破，使其比上游洛古河开河提前，比预报早4 d开河，本次预报的预见期超过24d，根据《水文情报预报规范》（（GB/T 22482-2008）），预见期＞15 d允许预报误差7 d，2017年开河日期预报值和实测值在误差均小于允许误差，且准确预报冰坝发生情况。

致谢：感谢国家气象局、黑龙江省水文局和国家科技基础条件平台建设项目“地球系统科学数据共享平台（www.geo⁃data.cn）”为项目研究提供数据支持。

参 考 文 献：

［1］ BELTAOS S.Progress in the study and management of river ice jams［J］.Cold Regions Science and Technology，2008，51：2-19.

［2］ SHEN H T，CHEN Y，WAKE A.Lagrangian discrete parcel simulation of two dimensional river ice dynamics［J］.International Journal of Offshore and Polar Engineering，1993，3（4）：328-332.

［3］SHEN H T，WANG D S.Under cover transport and accumulation of frazil granules［J］.Journal of Hydraulic Engi⁃neering，1995，120（2）：184-194.

［4］ SHEN H T.Mathematical modeling of river ice processes［J］.Cold Regions Science and Technology，2010，62（1）：3-13.

［5］ 杨开林，刘之平，李桂芬，等.河道冰塞的模拟［J］.水利水电技术，2002，33（10）：40-47.

［6］ 杨开林.冰盖河渠水深平均流速的横向分布［J］.水利学报，2015，46（3）：291-297.

［7］WANG J，HE L，CHEN P P.Numerical simulation of mechanical breakup of river ice-cover［J］.Journal of Hy⁃drodynamics，2013，25（3）：415-421.

［8］ 王军，章宝平，陈胖胖，等.封冻期冰塞堆积演变的试验研究［J］.水利学报，2016，47（5）：693-699.

［9］ 王军，陈胖胖，隋觉义.稳封期天然河道冰塞堆积的数值模拟［J］.水利学报，2011，42（9）：1268-1276.

［10］ 茅泽育，吴剑疆，张磊，等.天然河道冰塞演变发展的数值模拟［J］.水科学进展，2003，14（6）：700-705.

［11］ 郭新蕾，杨开林，付辉，等.南水北调中线工程冬季输水冰情的数值模拟［J］.水利学报，2011，42（11）：1268-1276.

［12］ 郭新蕾，杨开林，杨淑慧，等.长距离明渠系统反向输水冰情模拟［J］.水利学报，2015，46（7）：877-882.

［13］ SPYROS Beltao.River Ice Breakup［M］.USA：Water Resource Publication，2008.

［14］ FU H，YANG K L，GUO X L，et al.Safe operation of inverted siphon during ice period［J］.Journal of Hydrody⁃namics（Ser.B），2015，27（2）：204-209.

［15］ FU H，GUO X L，YANG K L，et al.Ice accumulation and thickness distribution before inverted siphon［J］.Jour⁃nal of Hydrodynamics（Ser.B），2017，29（1）：840-846.

［16］ 陈守煜，冀鸿兰.冰凌预报模糊优选神经网络BP方法［J］.水利学报，2004（6）：114-118.

［17］ 王涛.冰情预报方法［M］.北京：中国水利水电出版社，2014.

［18］ 王涛，杨开林，郭新蕾，等.基于网络的自适应模糊推理系统在冰情预报中的应用［J］.水利学报，2012，43（1）：112-117.

［19］ BELTAOS S.A conceptual model of river ice breakup［J］，Canadian Journal of Civil Engineering，1984，17（2）：173-183.

［20］BELTAOS S.Numerical computation of river ice jams［J］.Canadian Journal of Civil Engineering.1993，20（1）：88-89.

［21］BELTAOS S.River Ice Jams［M］.USA：Water Resource Publication，LLC.1995.

［22］ 戴长雷，于成刚，廖厚初，等.冰情监测与预报［M］.北京：中国水利水电出版社，2010.

［23］ WANG T，YANG K L，GUO Y X.Application of artificial neural networks to forecasting ice conditions of the Yel⁃low River in the Inner Mongolia reach［J］.Journal of Hydrologic Engineering，2008，13（9）：811-816.

［24］ 王涛，杨开林.神经网络理论在南水北调冰期输水中的应用［J］.水利学报，2009，40（11）：1403－1408.

［25］ 王涛，杨开林，郭新蕾，等.模糊理论和神经网络预报河流冰期水温的比较研究［J］.水利学报，2013，44（7）：842-847.

［26］ MAHABIR C，HICKS F，FAYEK A R.Neuro-fuzzy river ice breakup forecasting system［J］.Cold Regions Sci⁃ence and Technology，2006，46：100-112.

［27］ MAHABIR C，HICKS F E，FAYEK A R.Transferability of a neuro-fuzzy river ice jam flood forecasting model［J］.Cold Regions Science and Technology，2007，48：188-201.