核电站融冰数值模拟及回水管布置优化研究

赵 新，练继建，欧阳群安

（天津大学 水利工程仿真与安全国家重点实验室，天津 300072）

1 问题的提出

寒区核电站工程引水明渠在冬季引水过程中，为保障电站安全运行，需要开展防冰设计研究。引水渠道中冰害防治的运行方法主要有排冰法、蓄冰法和冰盖下输水［1］等，在技术措施方面主要有保温盖板法［2］、曝气扰动法和太阳能法等。上述方法和措施或者对冰害控制的时效性较差，或者对外界环境有较强依赖而融冰保障度较低，不适合用于核电站引水渠道的防冰设计。增温融冰方法是目前解决引水渠道冬季冰害比较理想的一种方法［3-5］。结合核电站具体情况，可以将部分机组冷却水回流至进水口断面，提高进水口附近水体温度，融化其中的水内冰。为确保融冰效果，有以下两个主要问题亟待解决：（1）冷却水回流结构如何设计才能够最大限度地发挥融冰能力；（2）不同冰情条件下融冰所需要的机组冷却水回流流量。

Osterkemp［6］初步研究了水内冰的初始成因；Omstedt［7］对水内冰的形成过程进行了数值计算，但是没有考虑水内冰在运移过程中的演变；隋觉义等［8］结合原型观测，采用模型试验方法研究水内冰和冰塞演变规律；吴剑疆等［9］采用数学模型模拟了天然河道地水内冰演变过程；王晓玲等［10］分析了某水电站引水渠道水内冰的演变规律。

综上所述，目前对核电站增温融冰研究的报道还不多见。本文针对紊流条件下的水内冰相变计算难题，提出紊动条件下水内冰相变计算方法，并以上述核电站为例在有限元分析计算中应用该方法，对融冰回水管的布置和融冰运行方式展开研究，研究成果可为类似工程设计提供参考。

2 电站融冰模型和方法

2.1 紊动条件下水内冰相变计算 淡水的冰点在0℃，而海水由于含盐量较大，冰点较淡水低，并且随着盐度的增加而降低。Kester［11］对海水冰点温度与盐度的关系进行了试验分析，得到如下关系式：

式中：Tf为冰点温度，℃；S为海水盐度，‰；Z为水深，m。

厂址海域冰点温度计算可知为-1.6℃。同时根据实测资料，厂址海域海水冰点温度为-1.5℃，两者较为接近，在下面的计算分析中以实测资料-1.5℃作为厂址海域的冰点温度。

海水温度升高需要吸收热量（比热容），水内冰融化也需要吸收一定的热量（潜热）。由于海水中含有盐类等矿物质，其比热容、潜热同淡水比略有差别。在紊动条件下，水内冰的相变过程非常复杂，热力学严格地讲具有不可逆性，因此海水的冻结点温度是一个点。融化是一个温度带，其起始点比冻结点略低，融化点接近零度，于是设定海冰融化相变温度带ΔT为-1.5～0℃。也就是说当海水温度达到0℃时，即认为海水中的水内冰已经完全融化。对原模型进行概化，忽略次要因素，重点关注在这一过程中的热量平衡，即：

式中：Tc为冷却水回流温度，℃；Cw为水的比热容，J/kg℃；λ为冷却水回流百分比；β为水内冰质量浓度，kg/m3；L为冰凌的融化潜热，J/kg；ΔT为相变温度带，℃。

假设紊动状态下，水内冰在海水中均匀分布，那么含有水内冰的海水将表现出不同的热力学特性，式（2）可转化为：

式中，Cwi为等效比热容，J/（kg·℃）。

2.2 有限元模型［12］

连续方程：

动量方程：

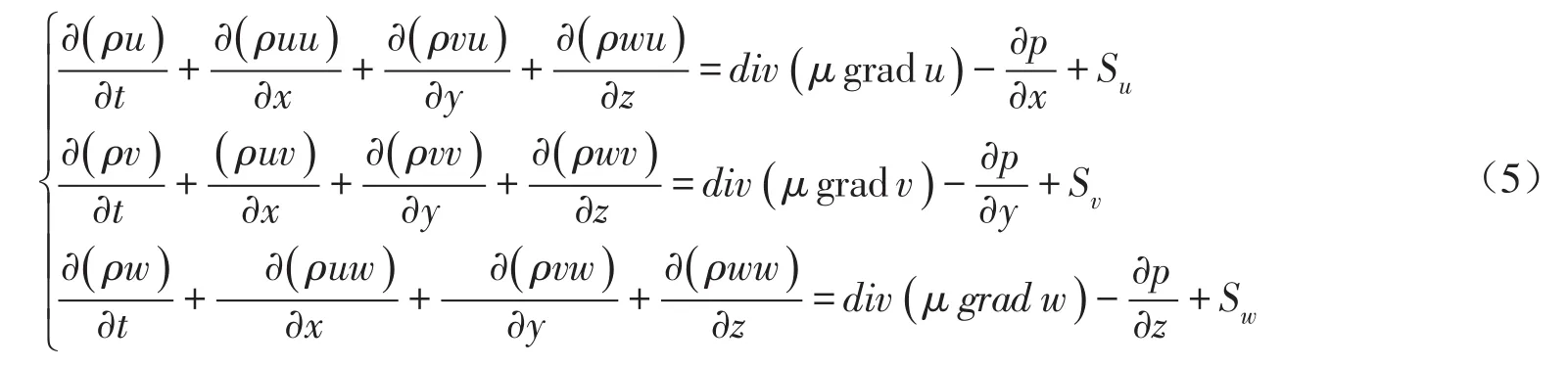
其中，广义源项S的定义为：

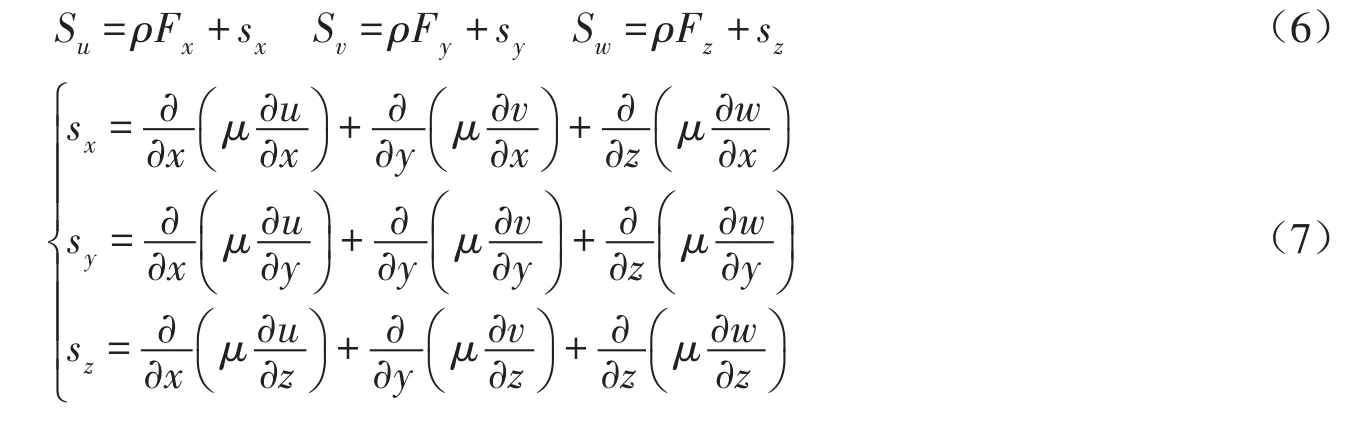
能量方程：

式中：u、v、w为沿坐标轴x、y、z方向的流速分量；ρ为流体密度；ρF为单位体积上的质量力；μ为动力黏度；I为内能；RIDIF为湍流换热项；TDIF为热传导项；RISOR为热源项，在本算例中为零。

考虑对流换热与热传导，忽略边壁热量损失及向空气中的热量扩散，湍流换热项RIDIF及热传导项TDIF表达式分别为：

紊流模型采用k-ε双方程模型，自由液面的捕捉采用VOF模型：

式中：F为流体体积分数；FDIF为流体分数扩散项；FSOR为流体体积源项；cF为湍流施密特数的倒数。

此计算模型中体积分数源项FSOR为0。

图1 单引水流道几何模型

图2 整体引水流道几何模型

建模范围总长度66.4 m，其中包含进水口前20 m长度的明渠段，进水口断面距粗过滤网45.4 m，距离细过滤网52 m，出水口断面距离细过滤网14.4 m。模型垂向高度为24.10 m，从底面高程-24.10 m到泵房高程0.00 m。单个流道几何模型如图1所示，整体模型如图2所示。

采用结构块网格剖分方法，整体网格尺寸为0.4 m，对冷热水混合主要混合区插入加密的嵌套网格，同时兼顾考虑计算速度与计算精度，冷却水回流管附近嵌套网格尺寸为0.1 m。进口边界采用压力入口条件，压力根据海面水位确定；出口边界采用流量出口条件，冷却水回流管道处设置为流量入口边界条件。

明渠引水的水温为-1.5℃（冰点温度），经过电站制冷循环系统后的回流冷却水水温12.11℃。

2.3 初始水内冰含量 在引水明渠前设置了多重防冰设施，包括破冰锥、拦冰网、拦冰索等，可以认为外来海冰都被阻滞在明渠外而无法进入明渠。而海水在引水明渠输送的过程中，将由于热量的散失而生成水内冰。忽略海水与渠道边壁之间的热量交换，忽略辐射的作用，重点考虑水体与空气之间的热量交换。基于水体连续性方程和热量平衡原理，构建出明渠一维水-冰相变输移控制方程，如下式：

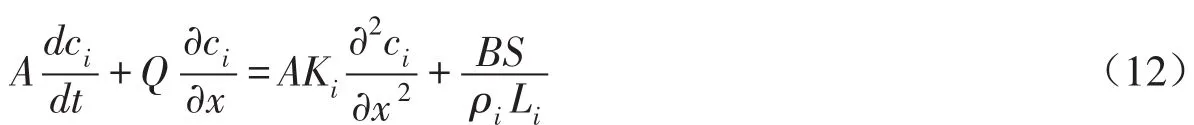
式中：ρi为冰的密度，kg/m3；A为过流断面面积，m2；Q为流量，m3/s；ci为水内冰的质量浓度；B为敞露水面宽度，m；S为河流单位面积上的热量损失，W/m2，主要为水面热量损失，水面热量损失可表达为Li为冰的融化潜热，J/kg；Ki为纵向扩散系数，m2/s，由于明渠长度较短，本文予以忽略。

引水明渠内水面线采用恒定非均匀渐变流微分方程计算：

式中；h为水深，m；i为底坡；Q为流量，m3/s；为水力坡度；α为流速修正系数，α≈1；B为水面宽度，m；g为重力加速度，m/s2；A为过流面积，m2。

经计算，平均高潮位0.58 m（85高程）条件下，机组引水口断面的最大水内冰质量浓度为0.84%。

图3 原设计方案侧视图

3 融冰效果和回水管布置优化

3.1 原设计方案融冰效果分析 原设计方案：设置1个回流管道，8个回水管道，排水方向竖直向下（如图3所示）。

在原设计方案下，冷却水通过回水管道竖直向下排出，但由于掺混位置距离细过滤网较近，掺混时间短，水体在到达细过滤网位置时难以完全消融水体中的水内冰。通过计算发现，1台机组运行工况下，需要近30%引水流量回流，才能够融化质量浓度0.84%的水内冰。接下来将对融冰回水管布置进行优化，以提高融冰效率，减少冷却水回流流量。

3.2 融冰回水管布置方案优化 融冰回水管布置优化主要从以下两个方向开展。

（1）优化回水管角度。回水管角度由原设计方案中的竖直向下改为倾斜向前，以促使冷热水体的掺混位置前移，提升回流水融冰效果。

（2）优化回水管数量。增加回水管道数量，在每个流道进水口处设置两个回水管，通过增加冷热水紊动点源的方法，提升回流水融冰效果。融冰回水管布置优化方案见表1和图4—7。

对13个优化方案分别建模，计算分析发现，增加回水管数量的同时减少了每个回水管的出水流量，从而导致冷热水掺混位置向下游方向移动，对融冰效果不利。在回水管角度优化方面发现，回水管水平向上倾斜10°时（优化方案4），与机组进水口前斜向下运动的水流对冲，冷热水掺混的位置显著向上游方向移动，冷热水之间的掺混效率最高，融冰效果最好（见图8）。

重点对优化方案4展开研究，计算分析不同运行工况、不同冰情条件下，所需要的冷却水回流流量。

3.3 冷却水回流量计算 选择平均高潮位0.58 m（85高程），设定0.1%、0.3%、0.5%、0.7%、0.84%5种水内冰质量浓度，计算工况如表2所示。

检修运行及正常运行时，不同水内冰质量浓度条件下，临界冷却水回流流量见图9。正常运行工况最小回流量大致为检修运行工况的两倍，这与前者的引水流量为后者的两倍是基本一致的，也就是说正常运行工况与检修运行工况的最小回流比基本一致，见图10。

图4 单管与斜坡垂直

图5 单管45°斜向下

图6 单管水平向前

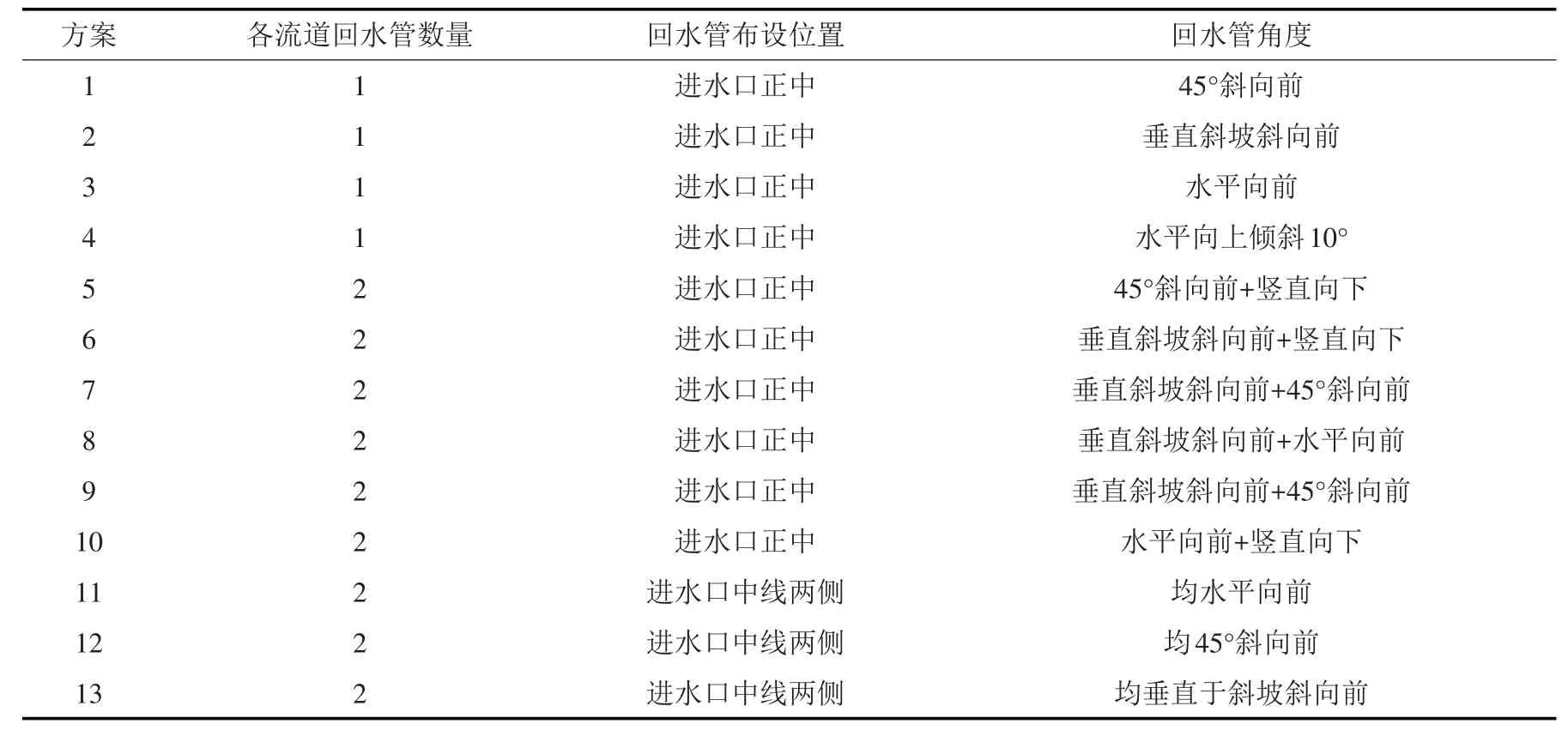
表1 融冰结构回水管布置优化方案

图7 单管10°斜向前

图8 最不利YZ截面温度场

表2 机组冷却水回流百分比计算典型工况

不同冰情条件下的融冰效率见图11，可以看到水内冰质量浓度越大，融冰效率越高，当水内冰质量为0.84%时，相应的融冰效率为30%。而当水内冰质量浓度较低时，融冰效率则较差。其中的关键影响因素在于水内冰质量浓度较低时，冷却水回流量也相应减小，导致冷热水初始掺混位置向下游方向移动，缩短了冷热水的掺混时间。

从冷却水回水管布置优化和冷却水临界回流流量计算两个方面，都可以发现提高核电站引水系统融冰效果的关键在于延长冷热水掺混时间，应尽可能采取措施促使冷热水初始掺混位置向上游方向移动，以提高融冰效率。

图9 冷却水最小回流流量

图10 冷却水最小回流比

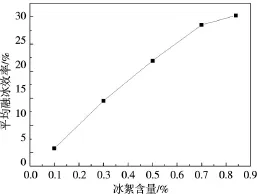
图11 不同冰情条件下的融冰效率

4 结论

针对寒区核电站引水渠道增温融冰方法，本文提出紊动条件下水内冰相变计算方法解决紊流条件下的水内冰相变计算难题，研究发现升温融冰方法的关键在于延长掺混时间。通过数值仿真的方法对寒区核电站进水口融冰回水管布置进行了优化，促使冷热水掺混位置向上游方向移动，提高了融冰效率；应用该方法对冬季冷却水回流流量进行了计算分析，结果表明，其保障了核电站引水渠道的融冰效果。在本算例中，冷却水融冰效率随水内冰质量浓度的增加而增大，当水内冰质量浓度为0.84%时，相应的融冰效率为30%。

参 考 文 献：

［1］ 赵新，练继建，黄焱.基于真冰模型试验的冰盖稳定性研究［J］.水利水电技术，2011（10）：132-13 6.

［2］ 穆祥鹏，陈文学，郭晓晨，等.高纬度地区渠道无冰盖输水的冰情控制研究［J］.水利学报，2013，44（9）：1071-1079.

［3］ 黄酒林，宗全利，刘贞姬，等.高寒区引水渠道抽水融冰原型试验及分析［J］.石河子大学学报：自然科学版，2014（3）：392-396.

［4］ 朱苗苗，刘焕芳，宗全利.高寒区引水渠道水温变化规律的试验研究［J］.石河子大学学报：自然科学版，2015（2）：239-243.

［5］ 赵梦蕾，刘贞姬，宗全利.引水渠道单井注水对不冻长度的影响［J］.中国农村水利水电，2016（4）：144-149.

［6］ OSTERKEMP T.Frazil ice formation：a review［J］.Journal of Hydraulics Division，1978，104（9）：1239-1255.

［7］ OMSTEDT A.Modelling frazil ice and grease ice in the upper layers of the ocean［J］.Cold Regions Science and Technology，1985，11：87-98.

［8］ 隋觉义，方达宪，汪德胜.水内冰冰塞堆积演变的研究［J］.水利学报，1994（8）：42-47，61.

［9］ 吴剑疆，茅泽育，王爱民，等.河道中水内冰演变的数值计算［J］.清华大学学报：自然科学版，2003（5）：702-705.

［10］ 王晓玲，张自强，李涛，等.引水流量对引水渠道中水内冰演变影响的数值模拟［J］.水利学报，2009，40（11）：1307-1312.

［11］ KESTER D R.Comparison of recent seawater freezing point data［J］.Journal of Geophysical Research，1974，79（30）：4555-4556.

［12］ 王福军.计算流体动力学分析［M］.北京：清华大学出版社，2004.