基于热示踪的饱和层状介质水热参数反演

潘梦绮 ，黄权中 ，冯 榕，黄冠华

（1.中国农业大学 水利与土木工程学院，北京 100083；2.中国-以色列国际农业研究培训中心，北京 100083）

1 研究背景

地下含水层的水力、热力学特性对于定量描述多孔介质中水、热运移过程具有重要意义，因此参数的识别和估计是介质中水热耦合迁移模拟中一个主要的问题，其中多孔介质水力传导度是决定含水层水分运动的重要参数［1-2］。传统的水文地质方法通常耗费人力、物力资源巨大，适用的尺度范围有限。而热示踪方法以温度作为监测指标，具有无污染、易测量等显著优势［3］，近年来被广泛应用于地表水与地下水交换［4-5］、工程地下水渗漏探测［6-7］以及土壤及含水层的水热参数反演［8-10］等方面。

大量基于室内和田间实验的研究表明，热示踪可在一定程度上较准确反演介质水、热特性参数［8-13］，且同时利用介质水热信息可提高参数的反演精度。王伟等［8］研究表明考虑热弥散可提高模型模拟低温水入渗土壤的温度变化的准确性。Nakhaei和Šimůnek［11］将土壤水分温度与累积入渗量同时用于多个水热参数的反演，所获得的参数具有较高的估算精度。尽管如此，实验中采用的原位观测手段，仍存在测点数量有限且会破坏介质结构等局限。基于热示踪的参数反演需要建立在对温度场准确描述和科学计算的基础上［3］，具有高时空分辨率的表面温度成像技术则为精确的反映较大范围内介质水热动态变化过程提供了可能。Steenpass等［12］将土壤表面热像温度与土壤剖面含水率、电导率值相结合以反演获得层状土壤的VG模型参数。Bateni等［13］将遥感陆面温度与数据同化模型相结合用于反演表层土壤物理参数。目前的研究多集中在利用表面热成像温度进行均质介质参数反演的情形，而对非均质介质参数反演的情况则不多见。

本文以石英砂为实验材料，开展了饱和稳定流场条件下层状介质的热示踪实验，分别采用热电偶及热成像两种测温方法测定砂箱内部与表面温度，结合了水热耦合模型，并利用HYDRUS模型的反问题算法对介质水热参数进行反演，并分析层状介质对水流运动的影响，从而获得饱和层状介质中水热迁移规律及参数反演方法。

2 材料与方法

2.1 实验装置与材料 本文设计了一套模拟饱和层状多孔介质水热运移过程的实验装置，整个装置由供水装置、有机玻璃砂箱、热传感装置、数据采集器及出水装置等几部分构成，如图1所示。

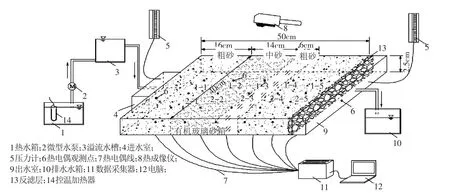
图1 热示踪实验装置示意图

有机玻璃砂箱的填装尺寸为50 cm×40 cm×2.5 cm（长×宽×高），砂箱左侧中部设长度为15 cm的进水室，右侧设长度为40 cm的出水室。为使流场稳定均匀，进水、出水室与填装介质间均设置多孔隔板，在出水室隔板左侧设置5 cm厚反滤层以防止细小颗粒随水流进入出水室并堵塞多孔隔板。砂箱内壁表面，垂直于水流方向每隔5 cm涂抹混有适量中砂颗粒的环氧树脂以减小壁面效应。砂箱背面设置20个均匀分布的热电偶观测点，进水、出水室内部分别设置2个热电偶（型号：T型；精度：±0.01℃；产地：美国）观测点，热电偶一端埋设于介质内部，一端与数据采集器（型号：CR3000；产地：美国）相连。砂箱上方垂直于砂箱表面80 cm高度处设置一台红外热成像仪（型号：Ti110；量程：-20～250℃；测量精度：±0.1℃；分辨率：150×120像素；产地：美国）。供水部分主要由溢流水槽、热水箱及微型水泵组成。溢流水槽与砂箱进水室相连，并由微型水泵（扬程：4.0 m；流量：1～3 L/min；产地：中国）供水，为砂箱提供恒定水头；在热水箱中安置一控温加热器（量程：0～99℃；精度：±0.1℃；产地：中国）为砂箱提供恒温热源；出水室与排水水箱相连。进水、出水室均设有压力计（量程：0～100 cm；精度：±0.1 cm；产地：中国）。

实验材料为三种不同粒径的白色精制工业石英砂，其基本物理性质如表1所示。砂箱从进水口到出水口分层填装，填装结构如图1所示。

表1 不同粒径石英砂基本物理性质

2.2 实验方法

2.2.1 热示踪实验方案 实验开始前先在恒定水头条件下注入常温水（22.7℃）使流场保持稳定，待出流量稳定且热电偶各观测点温度不再变化后，保持水头不变，使溢流水槽内的恒温水流（43℃）迅速注入进水室。实验过程中采用热电偶及热成像仪同时对砂箱内部与表面温度进行测定，测量频率均为1次/min。实验过程中同时对进水、出水室压力计读数、累积出流量进行监测和记录。当砂箱各观测点温度均达到稳定后实验结束。待砂箱冷却至室温，保持水头恒定，重复实验。

2.2.2 热成像温度处理 采用红外热成像仪对砂箱外部温度场进行测量时，其精度受被测物体表面发射率、测量距离、环境温度等因素的影响［18］，因此热成像温度与介质内部温度存在一定差异。热成像温度与介质内部温度换算过程如下：（1）先将热成像图像导入Smartview软件中进行处理，设置背景温度为22.7℃，砂箱表面发射率为0.92，透光率为100%；（2）根据斯蒂芬—玻尔兹曼定律［14］并借鉴Zou等［15］的计算方法，将热成像温度换算为砂箱表面的温度；（3）由砂箱表面温度与热电偶温度间的相关关系，将砂箱表面温度转换为介质内部温度。砂箱表面温度与热电偶温度相关关系如图2所示，两者存在着显著的线性相关关系，通过线性回归方程可将砂箱表面温度转换为介质内部温度。

图2 介质内部与砂箱表面温度间的相关关系

2.3 水热参数反演

2.3.1 二维水、热运移控制方程 本文采用HYDRUS模型的反问题算法对实验条件下水热迁移参数进行反演计算。水流运动控制方程为［16］：

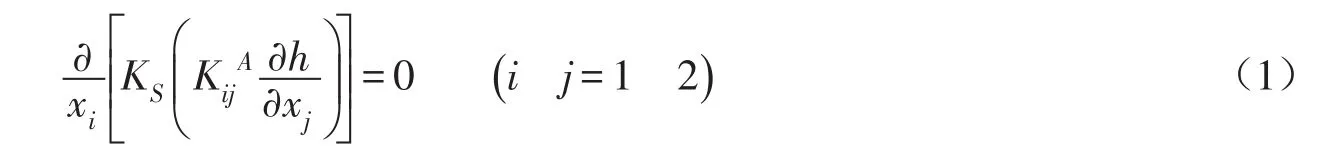
式中：h为压力水头，cm；xi为i方向笛卡尔坐标，cm；石英砂的饱和导水率，cm/min。

热运移控制方程为［17］：为各向异性张量KA的无量纲分量；KS为

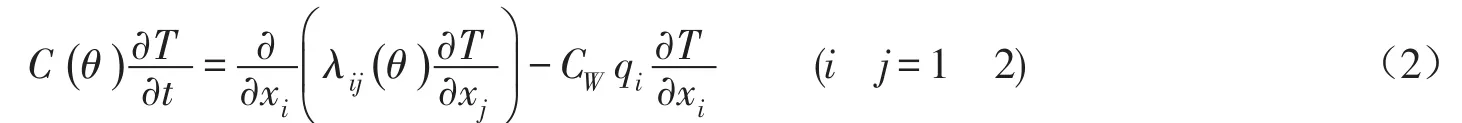
式中：λij（θ）为石英砂的表观热导率，Wm-1℃-1；C（θ）、CW分别表示多孔介质及水的体积比热容，Jm-3℃-1；qi为i方向达西流速，cm/min。

热运移控制方程忽略水汽弥散对热运移的影响。

其中多孔介质的体积比热容C（θ）具有广义可加性，可以表示为：

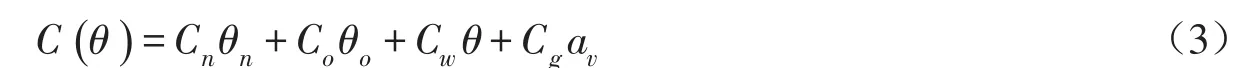
式中：θ为体积含水率，cm3/cm3；下标n、o、g、w分别表示多孔介质中固相、有机质、气相和液相。由于本实验介质为石英砂，并在饱和状态下进行实验，则可以认为不包含有机质及气相两部分。

式（2）中λij（θ）为多孔介质的表观热导率，根据de Marsily表观热导率λij（θ）可以表示为［18］：

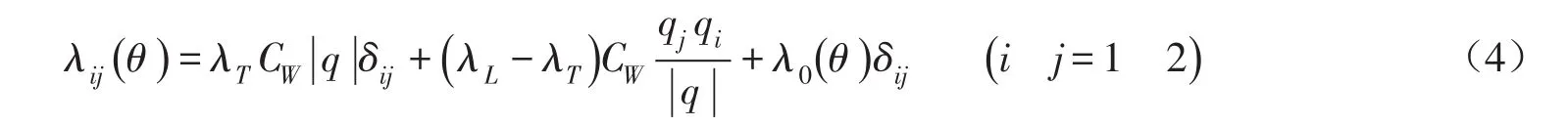
其中，多孔介质热导率λ0（θ）为：

式中：q为达西流通量密度，cm/min；δij为Delta函数，λL、λT分别表示纵、横向热弥散度，cm；b1、b2、b3为计算热导率的经验参数，［WL-1K-1］。

HYDRUS模型采用有限元方法求解水热运移方程，式（2）中i方向达西流速qi为：

式中：Kn为第n个单元顶点饱和导水率的算术平均值，cm/min；Ne为有限元的单元数；Ae为任一单元面积，cm2；x、y分别为任一单元的顶点坐标，cm。

2.3.2 初始条件及边界条件 将50 cm×40 cm的模拟区域划分为2000个1 cm×1 cm的网格，网格的材料划分与实际填装结构相同，如图1所示。模拟区域的上边界为供水边界，下边界为排水边界，且均为定水头边界，水头差为10.5 cm。上、下温度边界分别为进水、出水室内热电偶温度时序曲线，且均为第一类温度边界。其余边界均为零通量边界。模拟区域初始含水率为饱和含水率，初始温度为22.7℃。模拟时长与实验时间保持一致，取值53 min。

2.3.3 参数的设置及反演 石英砂各组分体积比热容取值参照文献［11］，热导率经验参数的设置则根据3种粒径均质石英砂的热示踪试验反演获得，参数详细取值如表1、2所示。并由实验数据对模型中饱和导水率Ks、纵向热弥散度λL、横向热弥散度λT三个参数进行反演。根据Levenberg-Marquardt非线性优化算法，参数优化的目标函数为［11］：

表2 模型中预设的热力学参数

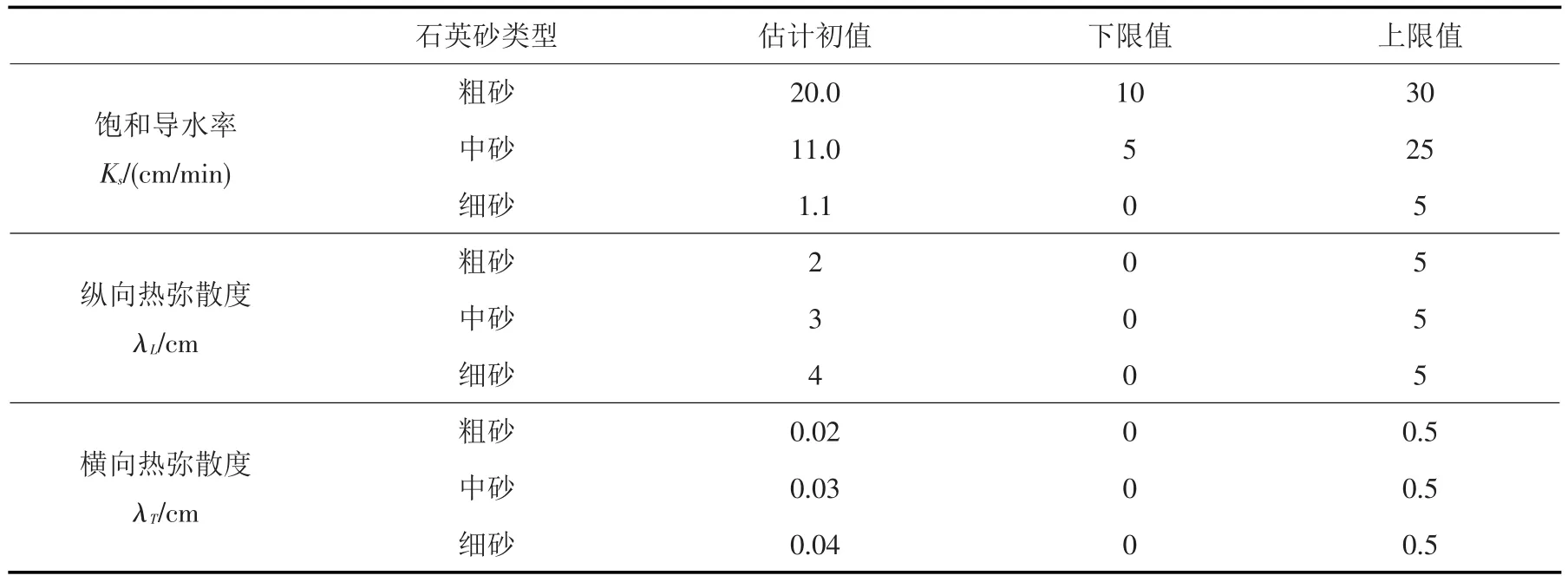
表3 待估参数的初值与估值区间

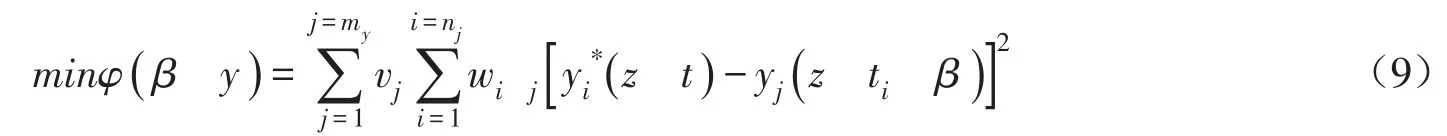
式中：yi*为实测的温度的动态数据；yj为相同测点、相同时刻下温度的模拟值；my为待估参数的类型；nj、wi，j分别为实测数据的数量及其权重。

本文分别利用介质内部与表面温度对石英砂待估参数进行反演，其初值及估算区间如表3所示。该参数优化的目标函数采用最速下降法进行求解［19］。

3 结果分析与讨论

3.1 层状介质的水热动态过程分析 热示踪实验开始后，与进水室内常温水逐渐混合的热水在恒定水头作用下进入砂箱。由于本实验采用部分线源方式注入，热运移峰以中部快，两侧较慢的非均匀分布方式不断向前运动。将相同实验条件下均质粗砂与层状介质的热成像温度进行对比（如图3所示）可以看出，当热量迁移至层状介质交界面时，热成像图像能捕捉到粗砂-中砂界面处热流峰面出现明显的“收束”现象，表明当介质中存在细粒夹层时，热流峰面沿水流运动方向（x方向）推进速度下降，热量沿垂直于水流方向（y方向）运动范围扩大。当热运移锋面随水流迁移至粗砂-中砂交界面时，中砂的孔隙流速略有减小，热对流作用相对减弱，使得单位体积粗砂的热能略有增大，温度升高。同时本实验中上边界为部分线源的定水头边界，砂箱内的流场是非均匀分布的，当热运移峰运动至粗砂-中砂交界面时，同一时刻更高的温度能使热量以热传导方式沿x、y方向迁移范围扩大。又由于粗砂导热性能较中砂更强，因此使分层界面处热量沿y方向迁移范围扩大更显著，从而导致热运移锋面在粗砂-中砂界面处出现明显的层间变化。

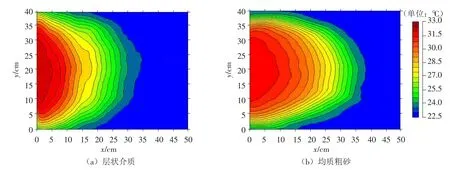
图3 相同时刻（t=15min）层状介质及均质粗砂条件下热成像温度分布

当热流锋面运动至中砂-细砂交界面处时，热成像图像无明显的层间变化。此时界面两侧流场均匀且介质具有相同的达西流速，当水流从中砂运动至细砂层时热传导作用相对于热对流略有增强，使热量能更均匀的穿透厚度较小的细砂层。

由于层状介质中的粗砂-中砂交界面处温度呈现出显著的“收束”现象，将其与相同位置处均质介质温度分布进行比较，结果如图（4（a）—（c））所示。可以看出均质介质的热传输速率远大于层状介质的热传输速率，而层状介质中由于细颗粒夹层的存在使温度沿y方向分布更均匀。根据多孔介质热量传输理论，当介质中有水分运动时，热量传输主要受传导和对流的共同作用［16］。为进一步分析层状介质与均质粗砂的热量迁移差异，分别对粗砂-中砂交界面处（x=17cm）单位体积均质介质与层状介质的热量变化进行分析，其计算公式可以表示为：

式中：ΔQ为i时刻介质吸收的热量，J；ΔV为单位体积介质，取1 cm3；Ti为i时刻介质温度，℃；T0为初始时刻介质温度，℃。

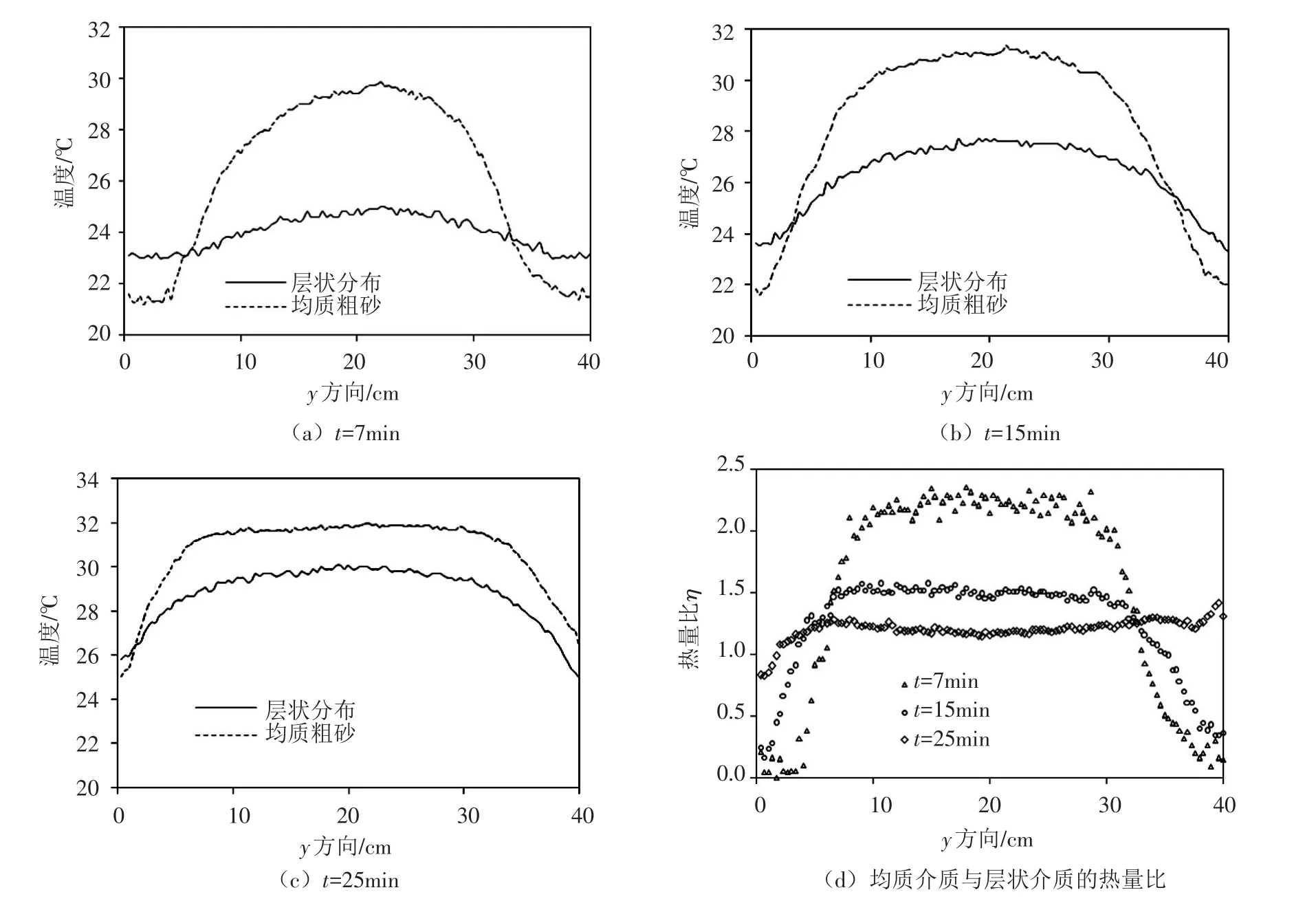
图4 不同时刻下相同位置处（x=17cm）均质与层状介质热成像温度与热量比分布

进一步计算单位体积均质介质与层状介质热量变化的比值，可以表示为：

式中：ΔQcs为任意时刻单位体积均质介质吸收的热量；ΔQms为相同时刻单位体积层状介质吸收的热量。

图4d为不同时刻下均质介质与层状介质热量比（η）沿y方向的分布，由于粗砂与中砂的导热系数差别不大，实验前期介质热量变化的差异主要由对流引起。随着热量不断注入砂箱，由对流引起的热量变化差异逐渐减小；当t=25 min时，除两侧边界外，η沿y方向基本无变化，说明此时由对流引起的热量差异将不再反映层状介质与均质粗砂的水流运动差异。

3.2 水热参数的反演与分析 为进一步探究层状介质中水热迁移规律的影响因素，将热示踪实验结果与HYDRUS模型的反问题算法相结合对层状介质的水热参数进行反演与分析。由于本实验中的层状介质具有对称性，因此选取第一组及第二组（图1）介质内部温度对石英砂的饱和导水率及热弥散度进行估计。Nakhaei和Šimůnek通过设置不同反演参数对反演结果的可靠性进行了检验，初始值的设置、反演参数的个数和类型是保证结果精度及可靠性的关键［11］。根据大量的研究表明，同时对水力及热力学参数进行反演有利于提高模型参数反演的精度［8-13］。由于反演的参数间有相互影响，设置不同的反演初值所得结果会略有差异，因此需要通过设置不同初值反复试算最终获得较优的参数值如表4所示。结果表明，热电偶与热成像温度分别反演所得的三种石英砂水热参数基本一致，相对误差小于1%。可以看出，石英砂饱和导水率随粒径减小而显著降低，在饱和条件下多孔介质的孔隙结构是影响介质导水能力的主要因素［20］，虽然细砂的孔隙度较高（表1），但主要由小孔隙构成，因而出现其饱和导水率显著低于粗砂的情形。

石英砂纵向热弥散度随介质粒径的减小而增大，而横向热弥散则随介质粒径的减小而呈现逐渐减小的趋势。饱和介质的热弥散主要受表征单元体内的固体颗粒及流体的物理特性影响，因此热弥散度具有尺度效应且与介质自身的物理特性（包括粒径大小、孔隙分布等）有关［21-23］。与溶质弥散相似，热弥散能促使热量随水流运动至更大的范围；不同的是热量不仅可以随水流运动，还能通过固相与液相之间及固相与固相之间传导。由于细粒介质孔隙度（θs）高于粗砂，其孔隙流速（qe）相对较小，介质和水分（即固相与液相）间的热交换能力增强，纵向弥散度（λL）增大。纵向弥散度与横向弥散度是相互影响的参数，由于热弥散总是优先沿水流方向传导热量，此时沿垂直于水流方向迁移的热量则相应减少［22］，因此导致横向弥散度与纵向弥散度随粒径的减小具有相反的变化趋势。

反演结果还表明纵横热弥散比变化范围在10～120之间，该结果与普遍认同的纵向弥散度为横向弥散度的10或100倍的结论基本一致［21-23］。且纵横弥散比随粒径增大而逐渐减小，表明在孔隙尺寸较大的介质中纵、横弥散度差异较小，能使热量沿各方向分布更均匀，也是促使热量在粗砂中能沿y方向运动范围扩大的因素之一。从表4可知，反演结果决定系数为0.957，且平均误差平方和为0.67，相对较小。表明非均质介质基于热示踪的水热参数反演均具有一定的精度。

图5为典型观测点热电偶实测及模拟温度随时间变化的关系曲线，观测点2-2的温度变化规律与2-1相似。从图中可以看出，实验初期由于热水与进水室中原有的常温水逐渐混合，热电偶温度变化较小。随热流锋面不断向前推进，砂箱内部温度逐渐升高并趋于稳定的温度值。由于热量在迁移过程中存在辐射损失，且随着观测点与热源距离的增大，热量损失逐渐增多，因此较远观测点所达到的稳定温度低于热源温度。如图5所示，各观测点的模拟温度与热电偶实测温度拟合程度较高，其R2均大于0.95，相对误差（MRE）的绝对值均小于5%。模拟模型能较准确反映介质内部观测点温度随时间的变化规律。

表4 层状介质水热参数反演计算结果

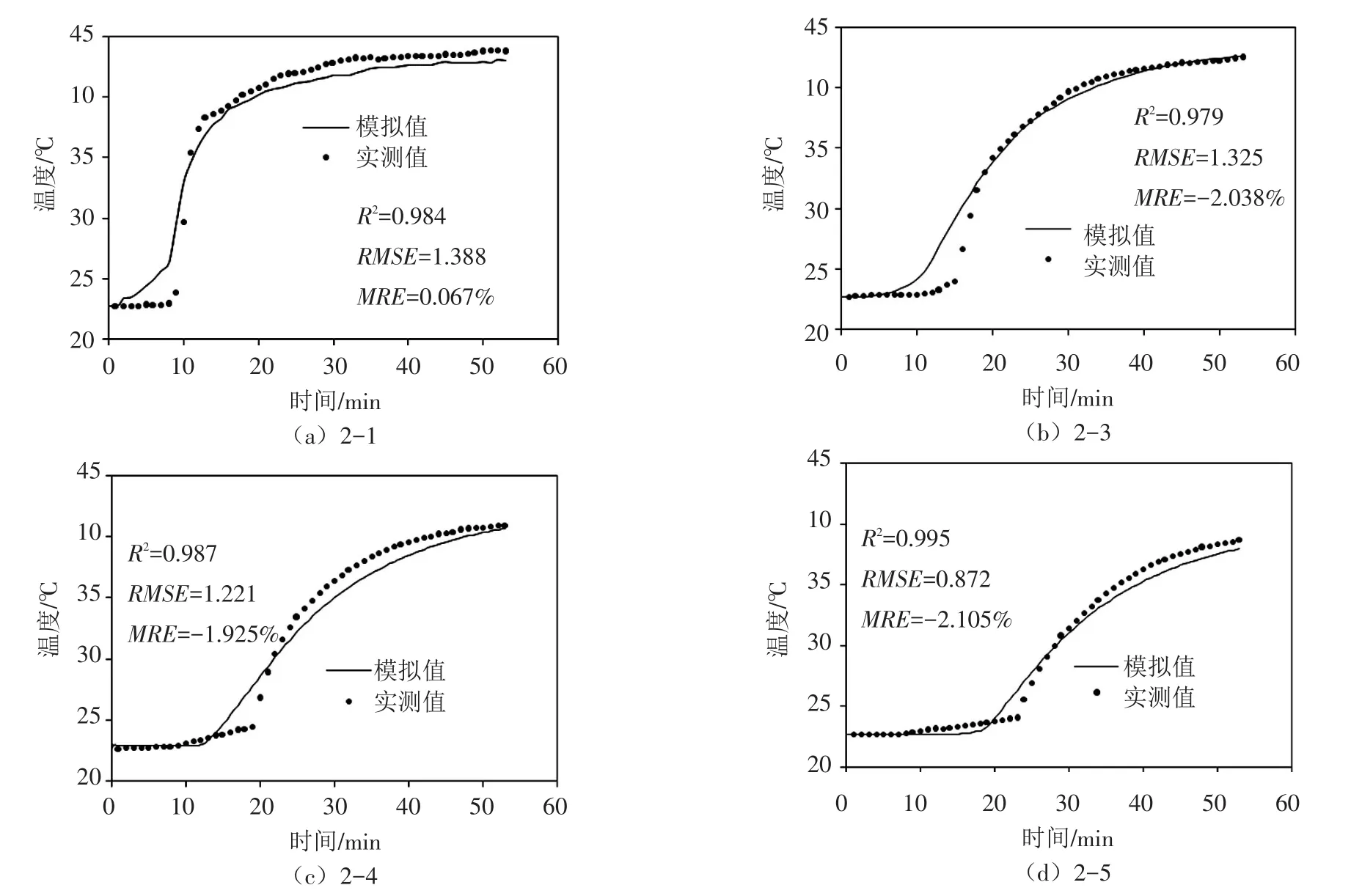
图5 典型观测点热电偶实测温度与模拟温度比较

3.3 水流通量估计误差影响因素分析 为进一步验证模拟模型中反演参数的合理性，将水流通量模拟值与实测值进行比较，相对误差达37.6%（表4）。对细砂饱和导水率的估计不足与热量散失是造成本实验水流通量估计误差大的主要原因。由于HYDRUS模型的反问题算法采用Levenberg-Marquardt非线性优化算法，优化参数的目标函数为非线性最小二乘估计。因此增加用于参数反演的温度测点数有利于提高反演参数的精度，反演所得的参数值也越稳定。同时对于水流方向与介质成层方向垂直的情况而言，细颗粒介质的导水率为水流运动的主要影响因素［24］。由于实验中流场为非均匀分布（图3（a）），因此用于参数反演的测点数量对参数估计的精度有着重要的影响。利用前面将热成像温度换算成介质内部温度的处理方法可增加细砂层的观测点，并应用到模型水热参数的反演过程中，进而探讨降低水流通量估计误差的方法。细砂层中用以参数反演的测点数分别为2、4、5、7、9、12、15和17个，反演结果表明随着细砂层测点数的增多，中砂与细砂拟合得到的纵向弥散度保持不变，而粗砂的纵向弥散度则略有减小，三种介质反演得到的横向弥散度基本一致。图6为水流通量估计误差与细砂层参数反演测点数的变化关系，从图中可以看出，模型对水流通量的估计误差随着细砂层观测点增多逐渐降低，当细砂层测点数增至4个以上时，模拟的水流通量的误差显著降低；当测点数量大于12个时，测点数量的增加不再显著提高模拟精度。通过增加参数反演中的测点数，水流通量的估计误差可从37.7%显著降低至20.7%，此时粗、中、细三种石英砂相应的饱和导水率分别为21.06、12.24、1.958 cm/min。

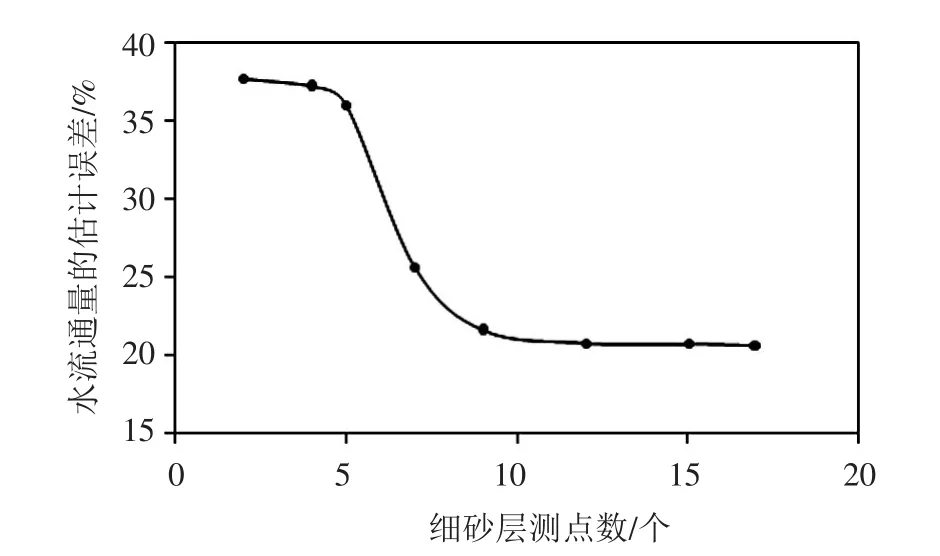
图6 水流通量估计误差与参数反演细砂层测点数量的关系

尽管通过增加细砂层中的测点数可以在一定程度上提高水流通量的反演精度，但水流通量的模拟值与实测值间仍存在一定的误差。热作为一种非保守型介质，迁移过程中时刻伴随着热量损失。在实验中热量随水流进入多孔介质，有机玻璃砂箱吸收了部分热量并进一步散失到周围环境中，使介质内部热量损失从而造成水流通量的估值偏低。热量损失对水热迁移过程及反演参数的影响还有待进一步研究。

4 结论

本文通过开展饱和层状石英砂的热示踪实验对层状介质中垂直于层面的渗流问题进行了研究与分析。实验分别采用热电偶及热成像两种测温方法对砂箱内部与表面温度进行测定，同时结合了HYDRUS模型中的反问题算法对层状石英砂的水热运移参数进行了反演。结果表明：

（1）当介质中存在细粒夹层时，热成像图像能反映非均匀流场中热流峰面在分层界面处出现的“收束”现象。层状介质中的细颗粒夹层可导致热流锋面沿水流方向迁移速率下降、热量沿垂直于水流方向运移范围加大、温度分布更均匀。对于热源持续输入的系统，热成像温度在实验前期能较好的反映层状介质对水流运动的影响。

（2）热示踪可在一定程度上反映层状介质中水流运动过程，与HYDRUS模型相结合可较好地用于反演介质水热运移参数。反演所得的饱和导水率估值随粒径的减小而显著降低，纵向热弥散度则随粒径的减小而增大，横向热弥散度变化趋势与之相反。纵横弥散比变化范围在10～120之间，且纵横弥散比随粒径减小而逐渐增大。

（3）对细砂饱和导水率的估计不足与热量损失是造成水流通量估计误差的主要原因，增加用于参数反演的测点数量有利于提高模拟精度，水流通量的相对误差由37.7%显著降低至20.7%。

参 考 文 献：

［1］ SU W G，JASPERSE J，SEYMOUR D，et al.Estimation of hydraulic conductivity in an alluvial system using tem⁃peratures［J］.Ground Water，2004，42（6）：890-901.

［2］ FERGUSON G.Heterogeneity and thermal modeling of ground water［J］.Ground Water，2007，45（4）：485-490.

［3］ 吴志伟，宋汉周.地下水温度示踪理论与方法研究进展［J］.水科学进展，2011，22（5）：733-739.

［4］ANDERSON M P.Heat as a ground water tracer［J］.Ground Water，2005，43（6）：951-968.

湿地经济合作开发模式是全方位的，还可以与湿地农业合作，组织湿地“农家乐”生态旅游产品吸引游客，学习种植莲藕、菱角、茭白、水芹；在濛洼、城东西湖、姜唐湖、寿西湖等行蓄洪区，充分利用当地特有的柳编、草编等特色手工业，组织生态旅游体验产品，游客自行购买原料，免费学习编织；与工业合作，组织参观污水处理厂，了解污水处理的过程；在采煤沉陷区旅游可以与煤矿企业、当地社区合作，建立湿地生态工业园，美化沉陷区生态环境，组织湿地旅游活动；与水利部门合作，依托大型水利工程和水利风景区，开展湿地生态旅游活动；与其他旅游景区合作，组织不同特色的湿地旅游线路，丰富湿地生态旅游产品内容。

［5］ CONSTANTZ J.Heat as a tracer to determine streambed water exchanges［J］.Water Resources Research，2008，44，W00D10.

［6］ 王新建，曾长女，许保田，等.基于温度场反分析的堤坝多个集中渗漏通道探测方法［J］.水利学报，2009，40（4）：486-491.

［7］ 王新建，朱大林，潘纪顺.利用温度全局优化法探测堤坝多重集中渗漏［J］.工程地质学报，2015，23（2）：335-343.

［8］ 王伟，赵坚，陈孝兵，等.基于VS2DH的低温水入渗模型验证及热弥散研究［J］.江苏农业科学，2013，41（6）：296-300.

［9］ GIAMBASTIANI B M S，COLOMBANI N，MASTROCICCO M.Limitation of using heat as a groundwater tracer to define aquifer properties：experiment in a large tank model［J］.Environmental Earth Sciences，2013，70（2）：719-728.

［10］WAGNER V，LI T，BAYER P，et al.Thermal tracer testing in a sedimentary aquifer：field experiment（Lauswie⁃sen，Germany）and numerical simulation［J］.Journal of Hydrogeology，2014，22（1）：175-187.

［11］ NAKHAEI M，ŠIMŮNEK J.Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code［J］.Journal of Hydrology，2014，62（1）：7-15.

［12］ STEENPASS C，VANDERBORGHT J，HERBST M，et al.Estimating soil hydraulic properties from infrared mea⁃surement of soil surface temperature and TDR data［J］.Journal of Vadose Zone，2010，9（4）：910-924.

［14］ INAGAKI T，YOSHIZO O.Surface temperature measurement near ambient conditions using infrared radiometers with different detection wavelength bands by applying a grey-body approximation：estimation ofradiative proper⁃ties for non-metal surfaces［J］.NDT&E International，1996，29（6）：363-369.

［15］ ZOU Z Y，HU Y H，GAO B，et al.Temperature recovery from degenerated infrared image based on the principle for temperature measurement using infrared sensor［J］.Journal of Applied Physics.，2014，115（4），043522.

［16］ BEAR J.Dynamics of Fluids in Porous Media［M］.New York：Academic Press，1972.

［17］ SOPHOCLEOUS M.Analysis of water and heat flow in unsaturated-saturated porous media［J］.Water Resource Research，1979，15（5）：1195-1206.

［18］ MARISLY G.Quantitative Hydrogeology［M］.London：Academic Press，1986.

［19］ DONALD W M.An algorithm for least-squares estimation of nonlinear parameters［J］.Journal of Society for In⁃dustrial and Applied Mathematics，1963，11（2）：431-441.

［20］ JIANG Y L，SHAO M A.Effects of soil structural properties on saturated hydraulic conductivity under different land-use types［J］.Soil Research，2014，52（4）：340-348.

［21］ RAU G C，ANDERSON M S，MCCALLUM A M，et al.Heat as a tracer to quantify water flow in near-surface sediments［J］.Earth Science Reviews，2014，129：40-58.

［22］ HOPMANS J W，ŠIMŮNEKJ，BRISTOW K L.Indirect estimation of soil thermal properties and water flux using heat pulse probe measurements：geometry and dispersion effects［J］.Water Resource Research，2002，38（1）：1-14.

［23］ CONSTANZ J，COX M H，SU G W.Comparison of heat and bromide as ground water tracers near stream［J］.Ground Water，2003，41（5）：647-656.

［24］ 王文焰，张建丰，汪志荣，等.砂层在黄土中的阻水性及减渗性的研究［J］.农业工程学报，1995，11（1）：104-110.