一类非线性发生率植被恢复模型的稳定性分析

纪德龙,李砚,赵新俊

（石河子大学理学院，新疆 石河子832003）

植被是生态系统中最基本也是最重要的元素，植被恢复不仅可以修复地表和地下的生态系统[1]，还对土壤理化性质[2]有极其重要影响。沙漠边缘区的环境恶劣，依靠人工保护措施是植被生态系统恢复的重要手段之一。目前，植被生态系统恢复的方式主要以人工保护措施为主，其中主要有围栏封育、人工植被重建以及改善植被退化的影响因子等方式。围栏封育可以改善土壤成分[3]和植被特征[4-5]，但过长的围封年限会导致植被结构和功能的退化[6]。影响人工植被重建的因素有很多，其中以植被蒸腾蒸发和土壤特性最为突出。通过对植被蒸腾蒸发[7]、土壤呼吸特性[8]的实验研究以及采用植被指标对退化草地植被效果进行综合评价[9]，为人工植被合理重建提供了一定的理论依据。在荒漠区，影响植被生长的关键因子地失调会导致植被生态系统的失衡，所以改善荒漠化驱动因子是植被生态系统恢复的根本手段。在遏制植被退化过程中，考虑空间尺度效应下的驱动因子[10]、沙漠化驱动因子的分类[11]及其动力学模型[12]，对遏制植被退化更具有针对性。随着现代科技的发展，人们开始利用RS、GIS技术和激光雷达图像研究大规模植被重建下的时空演变和植被退化特征[13-14]，这对植被恢复具有重要的意义。

以上文献主要围绕人工保护措施的方式及其影响因素进行研究，未能有效预测植被生态系统恢复状况以及恢复所用时间。荒漠区资源匮乏这一特性对植被人工修复有很大的遏制作用，从而对人工保护措施力度也提出了苛刻的要求。基于此，本文通过建立植被恢复模型定性分析人工保护措施力度对植被恢复的影响，并利用数值模拟验证所建模型的适用性，为失衡的植被生态系统更平稳的恢复平衡提供参考依据。

1 模型的建立

由于植被盖度大小与侵蚀大小是相互驱动的，故本文基于非线性发生率的SIS传染病模型，构造加入人工保护系数的植被恢复模型，并对其平衡点的稳定性进行分析。传染病模型的研究核心是对发生率的刻画，并且在经典的传染病传播模型中，还常常设定发生率是双线性的。Moghadas S M讨论了DS(Differential Susceptibility)和DI(Differential Infectivity)模型的标准发生率，并分析了2种模型的稳定性[17]。本文在Moghadas S M提出的DS和DI模型的标准发生率基础之上，针对植被被侵蚀后，人工保护措施对侵蚀速率 (即植被覆盖面积的动态变化)的影响，研究一类具有非线性发生率的被侵蚀植被恢复模型。通过加入人工保护措施因素预测植被恢复的动态变化，对资源匮乏的沙漠边缘区的植被恢复具有深刻意义。

基于SIS传染病模型[18-19]，构造加入人工保护系数的模型，其具体系统模型为：

其中：S表示t时刻健康且脆弱(即易被侵蚀)的植被覆盖面积；I表示t时刻被侵蚀植被的覆盖面积；r为内禀自然增长率；K为环境容纳量；β为侵蚀率；α为植被被侵蚀后，人工保护的作用系数；θ为自然恢复率；d为因植被被侵蚀后生长环境改变所造成的死亡率。系统中所有的参数均为正数。

为了证明和分析的简便，对系统模型(1)作变换dt=K(1+αS)dτ，则模型(1)变为

基于系统模型(1)、(2)的实际生态学意义，本文只在区域G={(S,I)|S≥0,I≥0}内讨论问题。

2 平衡点的存在性

引理1：模型(2)在G内总存在无侵蚀平衡点E0(0,0)和E1(K,0)，当θα＜β＜ad-γ/K时，模型(2)在G内存在唯一的侵蚀平衡点E2(S*,I*),即植被生态系统始终被侵蚀，但植被生态系统不会崩溃，其中

证明：分别令模型(2)中两式为0，即

可求得：

故模型平衡点分别为E0(0,0)、E1(K,0)和E2(S*,I*)。

引理1的生态学意义是：E0是无效的，即现实中不存在这中情况或导致系统发散，E1和E2与现实中的植被被侵蚀的状况相一致。

3 平衡点的稳定性分析

下面分析模型及其平衡点的稳定性[20-21]。由于模型(2)是模型(1)转换而来的，所以这2个模型具有相同的平衡点和系统稳定性。下面对模型(2)进行分析。其中，定理2-5都是在定理1的基础上展开分析证明的，定理2和定理3分别分析证明了平衡点E0(0,0)和E1(K,0)的稳定性，定理4和定理5分别证明了平衡点E2(S*,I*)的不同稳定性，二者属于一种递进关系。

定理1：模型(2)的一切正解一定有界。

证明：由模型(1)，令V=S+I，则

所以∨ε＞0,T＞0,当t＞T时，

因此，模型(1)的一切正解一定有界。

故模型(2)的一切正解一定有界，证毕。

定理2：无侵蚀平衡点E0(0,0)是不稳定的。

证明：模型(2)在E0(0,0)处的Jacobi矩阵为：

则系统(2)所对应的特征方程为

显然特征方程有2个正实根，故E0(0,0)是不稳定的。

定理3：当β＜θα时，无侵蚀平衡点E1(K,0)不仅是局部渐近稳定的，还在区域G内是全局渐近稳定的。

证明:(i)首先证明平衡点E1(K,0)的局部渐近稳定。模型(2)在E1(K,0)处的Jacobi矩阵为：

则模型(2)所对应的特征方程为

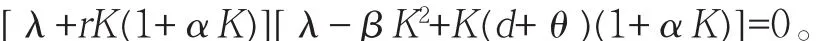
特征根λ1=-rK(1+αK)根为负实根；

又因为β＜θα，从而λ2＜0，故无侵蚀平衡点E1(K,0)是局部渐近稳定的。

(ii)再证明平衡点E1(K,0)在G内全局渐近稳定。事实上，当β＜θα时，模型(2)在区域G内存在唯一的无侵蚀平衡点E1(K,0)，而且平衡点处在边界上，故在区域G内不存在闭轨线，且模型(2)从G内出发的轨线均会一直停留在G内。又由于区域G的有界性，对任给的一个初始条件，模型(2)满足初值的解(S,J)最终都会趋于平衡点E1(K,0)，再由平衡点E1(K,0)的局部渐近稳定性，知可E1(K,0)是全局渐近稳定的。

由上面定理推导可知：在所研究区域内，无论初始被侵蚀植被生态系统有多么脆弱，最终被侵蚀植被生态系统都会转化为健康的植被生态系统。

定理4：当θα＜β＜αd-r/K时，被侵蚀平衡点E2(S*,I*)是局部渐近稳定的。

证明：模型(2)在E2(S*,I*)处的Jacobi矩阵为：

其中：

再由Hurwitz判别法可知:

当θα＜β＜αd-r/K时，侵蚀平衡点E2(S*,I*)是局部渐近稳定的。

从上述定理可知，模型(2)在侵蚀平衡点E2(S*,I*)的邻域内是吸引的。若初始点(S0,I0)在其邻域内，则模型(2)所描述的系统是稳定的，即随着时间推移，植被生态系统会达到一种平衡状态；若初始点不在(S0,I0)其邻域内，模型(2)就有可能是不稳定的，即随着时间推移，植被生态系统就有可能趋于崩溃状态。

定理 5：当θα＜β＜αd-r/K且Kα-1＜0时，侵蚀平衡点E2(S*,I*)在G内是全局渐近稳定的。

根据定理4可知：一旦植被被侵蚀，侵蚀状态就会一直存在，最终的植被易被侵蚀覆盖面积S和被侵蚀覆盖面积面积I将会稳定在S*和I*。

4 数值模拟及分析

4.1 数据来源

模型中涉及的参数是依据古尔班通古特沙漠南缘地区植被覆盖面积变化以及植被各等级度之间实际覆盖面积转移的百分比[22]赋值的，这使得参数更具有实际效果，从而更加准确地验证模型的适用性。

表1是从2001年开始到2005年，由于大型工程和居民活动导致植被生态系统失衡后，该地区植被覆盖面积的变化。

表2是2004年国家对古尔班通古特沙漠南缘地区实施人工保护措施后，2005-2008年植被覆盖面积的变化。

表3和表4分别是表1和表2的覆盖度等级之间的转移矩阵，其中植被覆盖度等级如下：a为覆盖度 0-0.1；b为覆盖度 0.1-0.2；c为覆盖度 0.2-0.3；d为覆盖度0.3-0.4；e为覆盖度>0.4。

表1 2001-2005年古尔班通古特沙漠南缘植被覆盖面积变化 hm2Tab.1 Vegetation coverage area variation of the south rim of Gurbantunggut from 2001 to 2005

表2 2005-2008年古尔班通古特沙漠南缘植被覆盖面积变化 hm2Tab.2 Vegetation coverage area variation of the south rim of Gurbantunggut from 2005 to 2008

表3 2001-2005年植被覆盖度之间的转移矩阵Tab.3 Transition matrix between vegetation coverage from 2001 to 2005 %

表4 2005-2008年植被覆盖度之间的转移矩阵Tab.4 Transition matrix between vegetation coverage from 2005 to 2008 %

依据表1和表2植被覆盖度面积的变化情况，确定未被且易被侵蚀的植被覆盖面积S为植被覆盖度等级c、d的实际面积之和，被侵蚀植被覆盖面积I为植被覆盖度等级a、b的实际面积之和。

4.2 参数的确定

4.2.1 环境容纳量的确定

从表1可以看出，2001年覆盖度等级为c的植被为82305 hm2，占所研究区域 90000 hm2的91.45%。

由以上数据可知，植被几乎未被侵蚀，植被生态系统正处于平衡状态。故此时的植被覆盖面积可近似看作已经达到环境承载量，这具有一定的合理性。故环境承载量等于各等级植被实际盖度面积之和，即K0=22400。由于作图时，取值不宜过大，故取K=22.4。

4.2.2 内禀增长率r的确定

在2001-2005年间，由于古尔班通古特沙漠南缘受到居民活动和大型工程的影响，其自然内禀增长率也受到很大影响。自2004年起，国家在此地区开始实施人工保护措施后，表2中围栏内覆盖度等级为c、d的植被覆盖面积不仅基数较大，而且增长相对稳定，故其转入转出的综合情况所体现的自然内禀增长率更加接近实际(由于e的等级范围过大，选取=0.5)。经分析，内禀增长率r由下列公式确定：

代入数据，可求得r=0.2470。其中：λi→j表示覆盖等级度i向覆盖等级度j转移的百分比，i(i=a,b,c,d,e)表示各覆盖等级度的平均值。

4.2.3 植被恢复率θ，被侵蚀率β，死亡率d、初值S0、I0和保护系数α的确定

（1）通过表1和表2的覆盖面积变化，以及表3和表4的植被等级度之间的面积转移百分比可知：对于植被覆盖等极度由b→c正向转化73.74%，故由可得，θ=0.4910。

（2）被侵蚀率β由c→b和d→b转移的综合情况确定，从而可得下列公式：

采用表2和表4数据，由上式解得β=0.0036。

（3）对死亡率d的确定，通过覆盖度等级为a,b的植被面积自身增长率和r之间的差距来确定。结合4.2.2可知，d=0.0245。

（4）对于初值的确定，通过表2数据并计算，可知2005年植被覆盖度等级为c、d实际覆盖面积之和为11000 hm2，植被覆盖度等级为a、b的实际覆盖面积之和为 7000 hm2，故令S0=11，I0=7。

（5）通过模型1的结构以及所确定的初值，并结合表3和表4的对比，可令人工保护系数α=0.8。

4.3 模型求解

将K=22.4，S0=11，I0=7，r=0.2470，θ=0.4910，β=0.0036，d=0.0245，α=0.8 代入模型(1)，并利用软件MATLAB7.1得到图1。

图1 模型（1）的数值模拟图Fig.1 Numerical simulation chart of model(1)

由图1可知：

（1）经过数年后，植被将逐渐趋于无侵蚀平衡点E1(K,0)，即植被生态系统无侵蚀。

（2）通过参数的选取可知β＜θα，该图符合定理3的结论。

4.4 补充性检验

由于模型 (1)中所涉及参数均是由2001年至2008年古尔班通古特沙漠南缘植被覆盖面积及覆盖度等级面积转移程度得到的，故图1的曲线走势与此地区2001年至2008年的植被覆盖面积有很大关联，图1中2005-2008年的植被覆盖面积并不能很好的验证模型的可靠性。为了充分检验模型(1)的预测功能，本文选取2010-2013年古尔班通古特沙漠南缘植被覆盖面积实际值[23-24]（通过文献中数据及数学反演得到），并通过模型（1）计算得出2010-2013年此地区植被覆盖面积预测值。具体数据如下：

表5 近年古尔班通古特沙漠南缘植被覆盖面积Tab.5 Vegetation coverage area of the south rim of Gurbantunggut from 2010 to 2013 hm2

利用软件SPSS对上述数据进行配对t检验分析，得到下列分析结果：

表6 配对t检验分析结果Tab 6 Pairingt-testing results

由表6可知：Sig.=0.303>0.05，这说明这两组数据显著性差异很小。由此可知，模型（1）的预测功能良好。

5 结论

由模型分析及数值模拟，并结合生态学原理，可得出以下结论：

（1）本文通过微分方程几何理论和生态学原理建立了植被恢复模型，该模型能有效预测植被恢复状况，以便当植被恢复状况异常时，能够及时查明原因并采取应对措施。

（2）在植被恢复过程中，通过调控人工保护措施力度，即当α≈β/θ时，可以更好地节省植被恢复所需资源，这对资源匮乏的沙漠边缘区的植被恢复具有重要意义。

（3）当β＜θα时，根据植被生态系统所具有的特性，随着时间推移，被侵蚀的植被生态系统将会逐渐恢复，毗邻已恢复植被生态系统地区的完全沙漠化地带(植物极其稀少或不存在)的植被数量与种类也会趋向于增多的态势。这表明：植被覆盖面积的增大，生态系统的不断修复，土壤中微生物数量及种类也会不断增多，进而改善土壤环境，促进植被生长，形成一种良性循环。

（4）当θα＜β＜αd-r/K且Kα-1＜0时，沙漠化面积会持续增大，侵蚀区域不断向外拓展。从模型平衡点分析上看，沙漠化侵蚀持续存在，其侵蚀速度较为温和，短时期内生态系统不会出现崩溃状态。这表明：随着沙漠化面积越来越大，沙漠化侵蚀速度也会越来越快，这就形成了一种恶性循环。因此，应加大保护力度，以改变参数之间的关系，以遏制沙漠化侵蚀。

6 讨论

（1）大多数文献通过植被生态因子的变化研究植被修复问题，由于实验方法的不同和生态因子的侧重点不同，其研究结果带有一定的主观性。本文所建立的模型，利用植被的种群特征及其数量关系，从宏观层面上研究植被修复问题，这使得研究结果更倾向于客观化。

（2）模型所涉及的参数由植被受保护前后若干年份的覆盖面积变化来确定，所以，实施人工保护措施后，并不能在短时间内预测未来植被恢复状态。另外，此类模型并未考虑自然降水的异常改变，一旦降水量变化过大，模型所涉及的参数就会出现差异，这对预测结果有一定影响。

（3）由于人工保护系数的改变，使得植被覆盖面积的内禀自然增长率、恢复率、非自然死亡率以及被侵蚀率产生变化，从而对植被生态系统恢复时间的预测也会产生较大的影响。因此，有待对模型(1)中相关参数之间的相互影响进行更深入的研究。

参考文献:

[1] 胡婵娟，郭雷.植被恢复的生态效应研究进展[J].生态环境学报，2012，21(9)：1640-1646.Hu C J，Guo L.Advances in the research of ecological effects of vegetation restoration[J].Ecology and Environmental Sciences，2012，21(9):1640-1646.

[2] 付标，齐雁冰，常庆瑞.不同植被重建管理方式对沙质草地土壤及植被性质的影响[J].草地学报，2015，23(1):47-54.Fu B，Qi Y B，Chang Q R.Effect of different revegetation management methods on the soil and vegetation characteristics of degraded sandy grassland[J].Acta Agrestia Since，2015，23(1):47-54.

[3] 杨新国，宋乃平，李学斌，等.短期围栏封育对荒漠草原沙化灰钙土有机碳组分及物理稳定性影响 [J].应用生态学报，2012，23(12)：3325-3330.Yang X G，Song N P，Li X B，et al.Effects of short-term fencing on organic carbon fractions and physical stability of sandy sierozem in desert steppe of Northwest China[J].Chinese Journal of Applied Ecology，2012，23(12):3325-3330.

[4] 安耕，王天河.围栏封育改良荒漠化草地的效果[J].草业科学，2011，28(5):874-876.An G，Wang T H.Effect of enclosure on restoration of degraded grassland[J].Pratacultural Science，2011，23(12):3325-3330.

[5] 刘雪明，聂学敏.围栏封育对高寒草地植被数量特征的影响[J].草业科学，2012，29(1):112-116.Liu X M，Nie X M.Effects of enclosure on the quantitativecharacteristics of alpine vegetation[J].Pratacultural Science，2012，29(1):112-116.

[6] 刘健，张克斌，程中秋，等.围栏封育对沙化草地植被及土壤特性的影响[J].水土保持通报，2011，31(4):180-184.Liu J，Zhang K B，Cheng Z Q，et al.Influences of fencing on vegetation and soil properties in sa ndy grassland[J].Bulletin of Soil and Water Conservation，2011，31(4):180-184.

[7] 张志山，李新荣，王新平，等.沙漠人工植被区的蒸发蒸腾[J].生态学报，2005，25(10):2484-2490.Zhang Z S，Li X R，Wang X P，et al.Evaporation and transpiration in revegetated desert area[J].Acta Ecologica Sinica，2005，25(10):2484-2490.

[8] 高艳红，刘立超，贾荣亮，等.沙坡头人工植被演替过程的土壤呼吸特征[J].生态学报，2012，32(8):2474-2482.Gao Y H，Liu L C，Jia R L，et al.Soil respiration patterns during restoration of vegetation in the Shapotou area Northern China[J].Acta Ecologica Sinica，2012，32(8):2474-2482.

[9] 王雪佼，靳瑰丽，朱进忠，等.放牧型退化草地植被重建效果的初步研究[J].新疆农业科学，2013，50(10):1893-1901.Wang X J，Jin G L，Zhu J Z，et al.Preliminary study on the effect of reconstructed grassland for grazing[J].Xinjiang Agricultural Sciences，2013，50(10):1893-1901.

[10] 郑伟，朱进忠.新疆草地荒漠化过程及驱动因素分析[J].草业科学，2012，29(9)：1340-1351.Zheng W，Zhu J Z.Analysis of desertification process and driving force factors in grassland ecosystem of Xinjiang[J].Pratacultural Science，2012，29(9):1340-1351.

[11] 彭羽，米凯，卿凤婷，等.影响植被退化生态因子的多尺度分析[J].应用基础与工程科学学报，2015，23(增刊):11-19.Peng Y，Mi K，Qing F T，et al.Spatial scale effects of ecological factors on vegetation degradation[J].Journal of Basic Science and Engineering，2015，23(Supplement):11-19.

[12] Jiao J，Cai S H，Li L M.Analysis of the Oasis Vegetation Degradation Dynamical model with Impulsive Irrigation in Arid Area[J].Mathematica Applicata，2016，29(2):409-417.

[13] 秦伟，朱清科，左长清，等.大规模植被重建背景下的黄土高原流域土地利用时空演变 [J].水土保持学报，2014，28(5):43-50.Qin W，Zhu Q K，et al.Spatio-temporal changes of Land use/cover driven by large-scale vegetation restoration on watershed in the loess plateau[J].Journal of Soil and Water Conservation，2014，28(5):43-50.

[14] 肖静.基于激光雷达图像分析的植被退化特征提取[J].激光杂志，2009，37(7):50-53.Xiao J.Vegetation degradation feature extraction based on the analysis of the laser radar image[J].Laser Journal，2009，37(7):50-53.

[15] 杜艳可，徐瑞，段立江.一类具有标准发生率的SIS型传染病模型的全局稳定性[J].数学的实践与认知，2009，39(10):140-144.Du Y K，Xu R，Duan L J.Global stability of an SIS epidemic model with standard incidence Rate[J].Mathematics in Practice and Theory，2009，39(10):140-144.

[16]朱慧强.具有非线性发生率和非定常人口的传染病传播模型分析[D].长沙：湖南大学，2012，39-48.

[17]Moghadas SM.Two core group models for sexual transmission of disease[J].Ecological modeling，2002，148(1):15-26.

[18] 陈兰荪.数学生态学模型与研究方法[M].北京：科学出版社，1988：11-34.

[19] 马知恩，周义仓，王稳定.传染病动力学的数学建模与研究[M].北京：科学出版社，2004：239-242.

[20] 马知恩，周义仓.常微分方程定性与稳定性方法[M].北京：科学出版社，2001：59-64.

[21] 张锦炎，冯贝叶.常微分方程几何理论与分支问题[M].北京：北京大学出版社，2000：31-37.

[22]刘乾.古尔班通古特沙漠南缘植物群落多样性与植被覆盖变化分析[D].乌鲁木齐：新疆农业大学，2009：48-52.

[23] 许玉凤，杨井，陈亚宁，等.近32年来新疆地区植被覆盖的时空变化[J].草业科学，2015，32(5):702-709.Xu Y F，Yang J，Chen Y N，et al.The spatial-temporal variations of vegetation cover in Xinjiang from 1982 to 2013[J].Pratacultural Science，2015，32(5):702-709.

[24] 许玉凤，杨井，李卫红，等.1982-2013年新疆不同植被生长时空变化[J].草业学报，2016，25(1):47-63.Xu Y F，Yang J，Li W H，et al.Spatial-temporal change in different vegetation growth of Xinjiang from 1982 to 2013[J].Acta Prataculturae Sinica，2016，25(1):47-63.