促进学生积累用方程解决问题的经验
———以“实际问题与方程”教学为例
课堂实录:
一、基于生活经验,理解问题情境
(播放足球比赛视频后,出示图1)

图1
师:从图中你知道了哪些数学信息?
生:足球上黑色皮是正五边形的,白色皮都是六边形的。
生:白色皮共有20块,比黑色皮的2倍少4块。
生:要求的问题是共有多少块黑色皮?
师:你有什么要提醒大家注意的?
生:五边形和六边形这个信息与要解决的问题没有关系。
生:我认为白色皮“比黑色皮的2倍少4块”这句话很重要。
师:像这样重要的关键句,对分析、解决问题很有用。
教学思考:理解问题情境是问题解决过程的起点,五年级的学生对足球有一些生活经验,从精彩的足球比赛情境引出数学问题,有助于激发学生的学习兴趣,让学生利用生活经验寻找问题情境中的有用信息和关键句,促进对问题情境的理解。
二、直观表征问题,积累画图经验
师:怎样把这些有用的信息表示出来才能直观看出这些数量之间的关系呢?
生:画图。
师:好方法!请你们试着画一画吧。
学生独立画图后,同桌互相解释自己所画的图,然后全班展示。
生1:我这样画的(如图2):

图2
师:你们感觉他画得怎样?
生2:不是很清楚,黑色皮和白色皮是两种东西,怎么画一条线段呢?
师:有不同的画法吗?
生3:我是这样画的(如图3)。
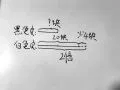
图3
师:能解释一下吗?
生3:(指图)这一段表示黑色皮,白色皮的2倍就画这样的2段,但题中说比2倍少4块,所以把这4块檫掉,这段就表示白色皮20块。(全班响起掌声)
师:还有要问这位同学的吗?
生4:你为什么要画两条线段呢?
生3:因为是两种皮,画两条线段表示更清楚。
生5:你那儿为什么要标一个“?”?
生3:因为黑色皮的块数不知道呀,这是题中要求的问题。
师:说得好,两种物品相比画两条线段表示更清楚,这个问号一标呀,题中的问题是什么就清楚了。
生6:我也画的线段图(如图4),不过比这位同学的改进了一下,多写了一个“2倍”。
生7:为什么要多写这个“2倍”?
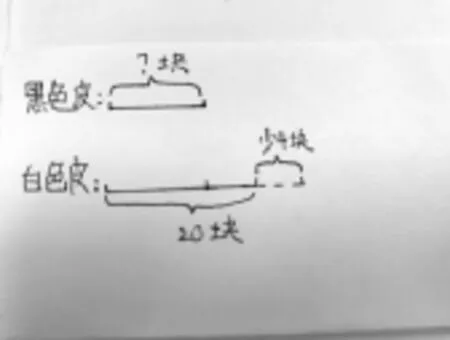
图4
生6:其实不写也感觉得到这段是这段的2倍(指图),不过写了更清楚。
师:其实这两位同学都画得不错,画的图不但表示出了两种皮的数量,还清楚地表示出了它们的关系。
教学思考:让学生用画图的方法表征问题中的数量及其关系,不但有助于使抽象复杂的数量关系直观形象化,促进学生对数量关系的理解,而且有助于学生感悟数形结合的思想,积累画图分析问题的经验。
三、寻找等量关系,构建数学模型
1.找等量关系。
师:通过画图直观表示出了白色皮和黑色皮之间的关系,根据前面学习的列方程的经验,你能用等量关系式来表示白色皮和黑色皮之间的关系吗?
(学生独立思考后全班交流)
生1:我列的等量关系是:黑色皮的块数×2-4=白色皮的块数。
师:同意吗?(生同意)说一说你是怎样找到这个等量关系的。
生1:我是通过“比黑色皮的2倍少4块”这句话来找到的。
师:能具体点吗?
生1:白色皮比黑色皮的2倍少4块,将黑色皮的2倍减去4块就等于白色皮的块数了。
师:好方法!通过关键句找到了等量关系。
(板书:黑色皮的块数×2-4=白色皮的块数)
师:看来顺着关键句的叙述就能很快找到等量关系。根据这一关键句你还能找到怎样的等量关系呢?
生2:黑色皮的块数×2=白色皮的块数+4,白色皮比黑色皮的2倍少4块,说明白色皮加4块就刚好等于黑色皮的2倍。
生3:黑色皮×2-白色皮的块数=4,白色皮比黑色皮的2倍少4块,也就是黑色皮的2倍比白色皮多4块。
师:同学们结合线段图从不同的角度思考找到了不同的等量关系,真棒!但老师发现写第一个等量关系的同学最多,为什么你们喜欢选这个呢?
生:我根据“白色皮有20块,比黑色皮的2倍少4块”这句话,自然就想到黑色皮的2倍减4块就是白色皮的块数。
师:真棒!所以我们在找等量关系时,应注意根据问题中的关键句顺题而想,方法就最简单了。
教学思考:正确找出等量关系是列方程解决问题的关键,学生以线段图为直观支撑,抓住问题中的关键句从多角度思考找出不同的等量关系,有助于培养学生思维的灵活性和广阔性品质,也有助于学生感悟找等量关系的方法,积累找等量关系的思考经验。
2.设未知数x,列方程。
师:找到了等量关系,接下来该干什么呢?(生列方程)这里该设谁为x呢?
生:黑色皮的块数是未知数,把它设为x,就可以当成已知数列出方程了。
(学生独立列方程后展示交流)
生1:2x-4=20。
生2:2x=20+4。
生3:2x-20=4。
师:你们能各自解释一下2x-4与20、2x与20+4、2x-20与4分别表示什么吗?
(生答略)
师:你们列的方程不同,但有共同的地方。发现了吗?
生1:都是设黑色皮为x。
生2:左右两边表示的都是一样的。
师:你的意思是说每个方程左右两边表示的都是同一种数量,对吧?
教学思考:有了等量关系作基础,学生借助已有列方程的经验,比较容易地将等量关系翻译成符号语言(等式)列出方程,让学生经历了抽象的过程,感悟了建模的思想。同时,引导学生反思方程左右两边数量表示的含义,促进了对方程的理解,让学生感受到用方程解决问题就是寻找相等关系的量构建等式。
3.解方程并检验作答(略)
四、反思总结步骤,提升思考经验
师:通过刚才的学习,你们认为用方程解决问题要经过哪几个步骤呢?
(学生独立思考、同桌交流、全班分享,最后教师梳出学生的意见,课件展示列方程解决问题的一般步骤,如图5)

图5
师:同学们再想一想,用方程解决问题的这几个步骤,与我们以前学习解决问题的“阅读与理解、分析与解答、回顾与反思”三大环节有什么联系?
学生独立思考后交流,最后教师点拨:列方程解决问题,首先也应阅读题目理解问题,然后通过分析数量关系、寻找等量关系、列出方程并求解等对问题进行分析与解答,最后通过检验、检查来回顾与反思问题解决过程与方法。
教学思考:经历列方程解决问题后,学生反思总结出列方程解决问题的步骤,并沟通列方程解决问题的步骤与问题解决一般环节的联系,有助于学生进一步感悟模型思想,形成用方程解决问题的思维模式,提升问题解决的经验。

